Численное моделирование жёстких систем с использованием (4,2)-метода

Моделирование процесса термического пиролиза этана для получения этилена является актуальной задачей. При решении таких задач требуется найти решение задачи Коши для систем обыкновенных дифференциальных уравнений, составленных на основе схемы реакций. Большая часть этих систем является жесткой по части фазовых переменных. Выполнение свойств жесткой системы влечет за собой большое различие в величине коэффициентов, что, в свою очередь, не позволяет применить к решению задачи Коши стандартные явные методы. В работах [1; 2] подробно описано построение (т,/)-методов для решения жестких систем дифференциальных уравнений, основанных на методах типа Розенброка. В данной работе описан (4,2)-метод, примененный к решению задачи Коши для нелинейной системы обыкновенных дифференциальных уравнений, соответствующей математической модели брутто-реакции пиролиза этана.

Рассмотрим брутто-реакцию пиролиза этана [3; 4]:

С2Н6 ^ С2Н4 + я2,

2С2Н6 ^ С2Н4 + 2СН4.

Соответствующие кинетические уравнения имеют вид

[С2Я6] ^ [С2Н4] + [н2],        W1 = к1С1,

2[С2Н6] ^ [С2Н4] + 2[СН],      ^2 = k2q2, где Ci — концентрация -того вещества, kj — константа скорости j-той прямой стадии, которые вычисляются согласно выражениям Аррениуса при температуре 800 К, таким образом к1 = 0.051, к2 = 0.7.

Составим систему обыкновенных дифференциальных уравнений, в которой фазовые переменные соответствуют концентрациям веществ, участвующих в реакции:

{ С 1 = — к 1 с 1 — 2к₂с 2 C 2 = k i C i +k 2 c 1 С з = к 1 С 1                                            ⁽ )

С₄ = 2к₂с 1

Поскольку начальный момент реакции присутствует только этан, то начальные условия будут иметь вид:

С1(0) = 1,С2(0) = 0,Сз(0) = 0,С4(0) = 0.                     (2)

Для нахождения изменений количественных характеристик реакции численно решим задачу Коши (1)-(2) (т, к) -методом и проведем сравнительную характеристику со способом решения методом Эйлера.

Используя (4,2)-метод четвертого порядка точности, разностную схему для каждого компонента вектора решения построенной модели можно представить в виде [1; 2]: 4

yⁿ⁺¹ = _уп + ^ _p._Q. ,_Dn = _Е- _aTf_n , i=1

D n 4 1 = Tf& n ), D n 4 2 = 4 1 , D n 4 3 = ^^f(y n ⁺ 0 31 4 1 ⁺ 0 32 4 2 ) + ^ 32 4 2 , D n 4 4 = 4 3 + « 42 4 2 '

где г - шаг интегрирования решаемой задачи, Е — единичная матрица размерности (4x4), yER⁴, 4 i ER⁴,y₀ = (1,0,0,0).

Вещественные коэффициенты, при которых схема обладает устойчивостью и 4-м порядком точности, a, pi, a. j ₂, 0_3к, 1 < i < 4,3 < j < 4,1 < 4 < 2 , имеют следующие значения [1; 2]:

a = 0.57281606248213,p_i = 1.27836939012447, p₂ = —1.00738680980438,p₃ = 0.9265539109350, p₄ = —0.33396131834691,0₃₁ = 1.00900469029922, 0₃₂ = —0.25900469029921, a₃₂ = —0.49552206416578, a₄₂ = —1.28777648233922.

Для системы (1) f(y) и f_n имеют вид

f(y) =

(- к 1 У 1 - 2k₂y 2 к 1 У 1 + к₂у !

км

\     2к 2 У 2

f n =

df(y)

ду

=( ^—

к 1 — 4к 2 У 1	к 1 + 2к 2 У 1	к 1 У 1	4к 2 У 1
0	0	0	0
0	0	0	0
0	0	0	0

)

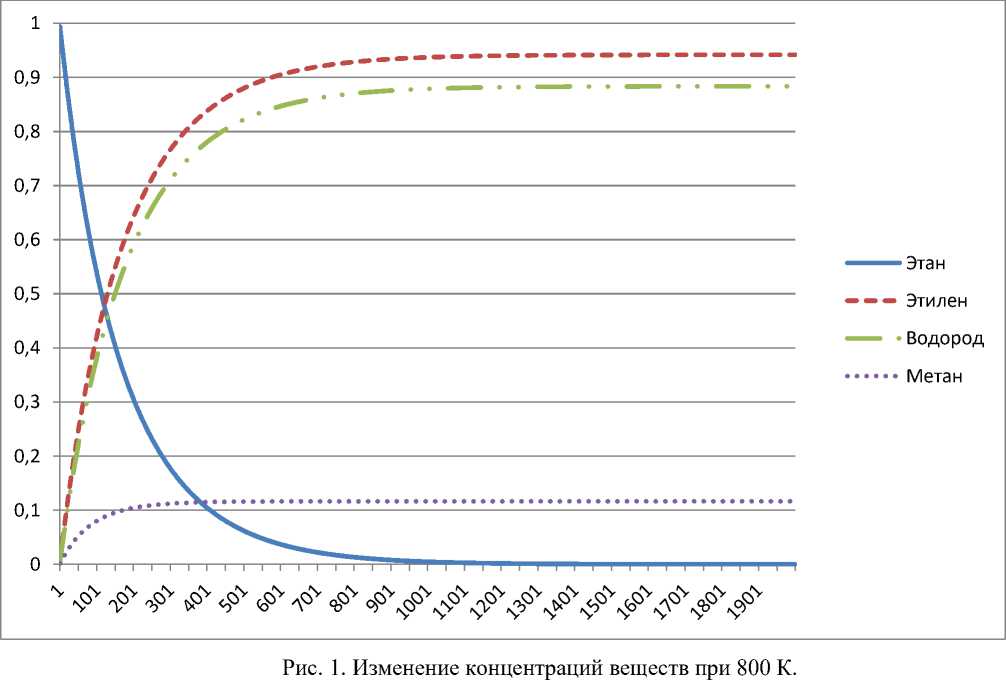
На основе построенной схемы был разработан программный комплекс для решения системы уравнений (1) с начальными данными (2). На рисунке представлены изменения концентраций веществ во времени при температуре 800 К. Для оценки эффективности (4,2)- метода эта же система была решена явным методом Эйлера, разностная схема для которого имеет вид [5]:

yn+1 = yn + Tf(yn).

Сравнительные результаты испытаний представлены в таблице 1, за опорное было принято решение, полученное с помощью системы Wolfram Mathematica с шагом т = 0.1.

Таблица 1

Результаты работы методов

Число итераций	Время выполнения		Точность, £
	Явный метод Эйлера	(4,2) — метод	Явный метод Эйлера	(4,2) — метод
10	6 мс	7 мс	0.034	0.001
50	59 мс	49 мс	0.00762	0.00055
93	105 мс	98 мс	0.0043	0.0001

Из таблицы 1 видно, что многостадийный метод имеет преимущество по времени выполнения, точности и корректности по отношению к явному методу.

Таким образом, сравнительный анализ показал эффективность (т, /с)-метода для решения жестких систем обыкновенных дифференциальных уравнений, в частности, для нелинейной системы обыкновенных дифференциальных уравнений, соответствующей математической модели брутто-реакции пиролиза этана, поскольку заданная точность достигается за меньшее количество итераций по сравнению с методом Эйлера.