Численное решение систем линейных алгебраических уравнений со случайными коэффициентами

Решение систем линейных алгебраических уравнений – одна из самых востребованных задач вычислительной математики. Они используются практически во всех разделах математического моделирования. К численному решению систем линейных алгебраических уравнений сводятся многие задачи математической физики, экономики. Однако при решении реальных практических задач коэффициенты матриц и правые части уравнений редко известны точно.

Один из подходов к численному решению задач с неточными данными – метод Монте– Карло [1].

При всех его положительных качествах этот метод обладает рядом недостатков. Одними из самых существенных из них являются низкая скорость сходимости и большой объем вычислений.

С середины 1960-х гг. стал развиваться альтернативный подход решения задач с неточными данными – интервальный анализ [2].

Для его реализации необходимо знать интервалы изменений случайных величин. Соответственно интервальный анализ дает только границы множеств решений исходных задач. В тех случаях, когда известны не только границы, но и функции плотности вероятности случайных величин, возможно применение численного вероятностного анализа, одна из первых работ этого направления [3].

В рамках обозначенного направления рассмотрим понятие численного вероятностного анализа как раздела вычислительной математики, предметом которого является решение задач со стохастическими неопределенностями в данных с использованием численных операций над плотностями вероятностей случайных величин и их функций. Одним из основных элементов численного вероятностного анализа является гистограммная арифметика, применение которой позволяет снизить уровень неопределенности в данных и получить дополнительную информацию о распределении случайных величин [4].

Идея гистограммного подхода изложена в работах [5, 6] и заключается в следующем: наряду с общими представлениями случайных величин своими плотностями в виде непре- рывных функций можно рассматривать случайные величины, плотность распределения которых представляет гистограмму. Например, в случае одномерной случайной величины гистограмма P - кусочно-постоянная функция, которая определяется сеткой {xt |= 0,...,п} и на каждом отрезке [xi, xi+1] принимает постоянное значение Pi, h = max"11{xi+1 - xi}.

Вероятностные расширения

Важным понятием численного вероятностного анализа является понятие вероятностного расширения. В рамках гистограммного подхода определим понятие гистограммного расширения. Для этого рассмотрим задачу определения закона распределения функции нескольких случайных аргументов.

Пусть имеется система непрерывных случайных величин ( x 1 ,..., x n ) с плотностью распределения p ( x 1 ,..., x n ). Случайная величина z связана с ( x 1 ,..., x , ) функциональной зависимостью:

z = f (x„..., x,).

Тогда плотность вероятности случайной величины z будем называть вероятностным расширением функции f .

На основе понятия вероятностного расширения определим гистограммное вероятностное расширение. Пусть гистограмма F определяется сеткой { z i |= 0 ,..., , }. Определим область Q= {( x 1 ,..., x n ) | z i <  f ( x 1 ,..., x n ) <  z i _{+ 1}}. Тогда значение гистограммы F i на отрезке [ z i , z i _{+ 1}] имеет вид [4]:

F = j ^ p ( 4 1 ,..., 4 , ) d . ... d ^ , / (--„ ---) .                                  (1)

Гистограмму F , построенную по (1), будем называть вероятностным гистограммным расширением f .

Далее построим гистограммные вероятностные расширения для арифметических операций над случайными величинами. Пусть P - гистограмма плотности вероятности z = x * y , где * е { +,-,-,/,^ }. Тогда величина P на интервале [ z i , z i _{+ 1}] определяется по формуле [4]:

Pi = L Р(x1, x2)dx1 dx2/(zi+1 - zi), где Qi =(x1, x2) | zi < x1 * x2 < zi+1}.

Операция max( x , y ) определяется через функцию распределения F :

F ( z ) = Г P x ( 4 ) d 4 ^z P y ( 4 ) d 4. -to -^

Пусть f ( x 1 ,..., x n ) - рациональная функция, тогда для вычисления гистограммы F заменим арифметические операции на гистограммные, а переменные x 1 , x ₂,..., x n - их гистограммными значениями. Полученную гистограмму F будем называть естественным гистограммным расширением.

Теорема 1 . [5] Пусть f ( x 1, . „ , x n ) - рациональная функция, каждая переменная которой встречается только один раз, и x 1,. „ , x n - независимые случайные величины. Тогда естественное гистограммное расширение аппроксимирует вероятностное расширение.

Рассмотрим пример, который иллюстрирует теорему 1. Пусть функция представлена в следующем виде:

f ( x , y )= xy + x + y + 1 = ( x + 1)( y + 1) .

Заметим, что только второе представление функции в виде произведения двух сомножителей попадает под условие теоремы 1 и, следовательно, естественное гистограммное расширение будет аппроксимировать вероятностное с некоторой точностью O ( h ^a ).

Теорема 2. [5] Пусть для функции f ( x_x ,..., x_n ) возможна замена переменных, такая что f ( z_x , .„, z k ) - рациональная функция от переменных z_x , .„, z k , удовлетворяющая условиям теоремы 1 и z_x - функции от множества переменных x i , i е Ind i , причем множества Ind i попарно не пересекаются. Пусть для каждой z_i можно построить вероятностное расширение. Тогда естественное расширение f ( z_x , .„ , z k ) будет аппроксимировать вероятностное расширение f ( X x ,..., X n ).

Пример 1 . Пусть f ( x _x , x ₂ = ( - x_x + x _x) sin ( x ₂). Тогда z _x = ( - x _x ² + x _x) и z ₂ = sin ( x ₂). Заметим, что можно построить вероятностные расширения функций z _x, z ₂, где f = z _x z ₂ - рациональная функция, попадающая под условия теоремы x. Следовательно, ее естественное расширение будет аппроксимировать вероятностное расширение f ( x _x , x ₂) .

Рассмотрим случай, когда для f ( x _x ,..., x_n ) необходимо найти вероятностное расширение f , но не удается построить замену переменных согласно теореме 2.

Алгоритм 1. Пусть для определенности только x _x встречается несколько раз. Заметим, что если подставить вместо случайной величины x _x детерминированную t , то для функции f ( t , x ₂ ..., x_n ) можно построить естественное вероятностное расширение. Пусть t - дискретная случайная величина, аппроксимирующая x _x следующим образом: t принимает значения t i с вероятностью P i и пусть для каждой f ( t i , x ₂ ..., x_n ) можно построить естественное вероятностное расширение ф _i . Тогда вероятностное расширение f функции f ( x _x ,..., x_n ) можно аппроксимировать плотностью вероятности ф следующим образом: n

Ф(О = £ ^р »№ )• i = x

Пример 2. Пусть f ( x , y ) = ² y + x , где x , y - равномерные случайные величины, заданные на [0 , x]. Заменим x дискретной случайной величиной t , { t i | t i = ( i - 0 . 5) / n ,= x , 2 ,..., n }, P i = x / n . Далее вычислим естественные вероятностные расширения ф _i . Сравнение ф и f , вероятностного расширения f ( x , y ) показало хорошее приближение. Анализ полученных результатов показал, что в данном примере ф аппроксимирует f с порядком a = x,4998:

II ф - № Cn-a, где C - некоторая константа, не зависящая от n .

Системы линейных алгебраических уравнений

Рассмотрим системы линейных уравнений

Ax=b, где x е R" - случайный вектор решения;

A = ( a ij ), b = ( b i ) - случайная матрица и вектор правой части. Предположим, что случайная матрица (a ij ) и вектор (b i ) имеют независимые компоненты с плотностями вероятности pa j , pb i соответственно.

Носитель множества решений можно представить в следующем виде [Dobr2004]:

X = {x | A= b, A е A, b е b}.

Пример 3. Пусть матрица A имеет вид

A =

' 2

< ^{- 1}

-

Предположим, что случайный вектор b состоит из независимых компонент b 1 , b ₂, каждая из которых есть случайная величина, равномерно распределенная на отрезке [0 , 1]. Тогда носитель плотности вероятности вектора b - квадрат [0 , 1]².

Построим функцию распределения случайного вектора x. Заметим, что вероятность того, что x < r и x2 < r2 равна площади, отсекаемой от квадрата [0,1]2 прямыми, проходя щими через точку b0 = Ar, где r = (r1,r2)г

с направляющими векторами 1 1 = (2 ,- 1)

1 2 = ( - 1 , 2) .

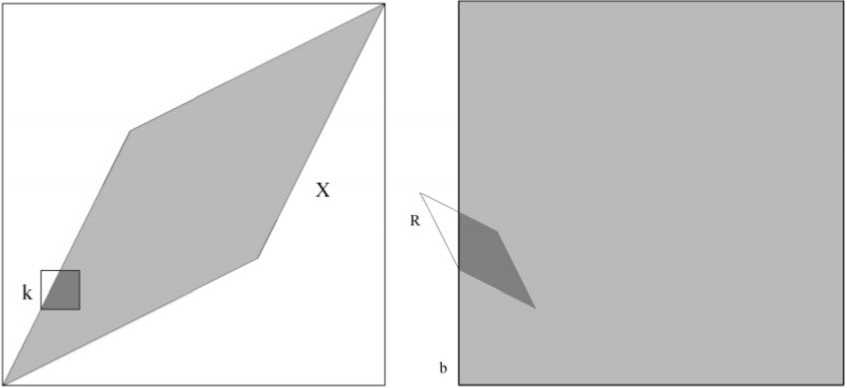
Рис. 1. Вычисление плотности вероятности вектора решений

На рисунке 1 в левой части серым цветом закрашено X - множество решений системы. Для вычисления вероятности попадания в квадрат к отобразим его с помощью матрицы A на вектор правой части b (правая часть рисунка). Квадрат к отображается в ромб R . Таким образом, вероятность попадания решения в квадрат к равняется интегралу от плотности вероятности вектора b по области пересечения ромба R и вектора правой части b .

На рисунке 2 приведено кусочно-постоянное с шагом h = 0,1 приближение совместной плотности вероятности вектора x . Сплошной линией проведена граница множества решений исходной системы. Величина вероятности в точности пропорциональна площади пересечения элементарного квадрата и множества решений.

Заметим, что при h ^ 0 приближение совместной плотности вероятности стремится к точному P_x - равномерному, с носителем, совпадающим с границами множества решений исходной системы. Непосредственными вычислениями легко убедиться, что

Ax = b.

Далее перейдем к случаю, когда A = ( a ij ) - случайная матрица. Каждому x е X можно сопоставить подмножество коэффициентов A x с A , b_x с b :

Qx = {A, b | Ax b, A е A, b е b}.

Заметим, что для фиксированного x коэффициенты матрицы и вектора правой части связаны соотношениями

n

Ea^x, -= 0,= 1,...,n, ijji j=1

следовательно,

n

Q= { A , b | ^ a_jjx_j - b i 0 ,= 1 ,..., n}.

j = 1

Пусть необходимо найти вероятность P ( X ₀) попадания решения х в некоторое подмножество X ₀ с X. Сопоставим X ₀ множество П ₀ = { П x | x е X ₀}.

Тогда

P ( X 0 ) =L П^П n 1 р» , П n 1 pb , d П.

ⁿ 0

Пример 4.

Рис. 2. Приближение совместной плотности вероятности вектора х

. Г a 11 A =

a ¹² 1

a 22 )

( a 21

Элементы матрицы a j состоят из независимых, равномерно распределенных компо-

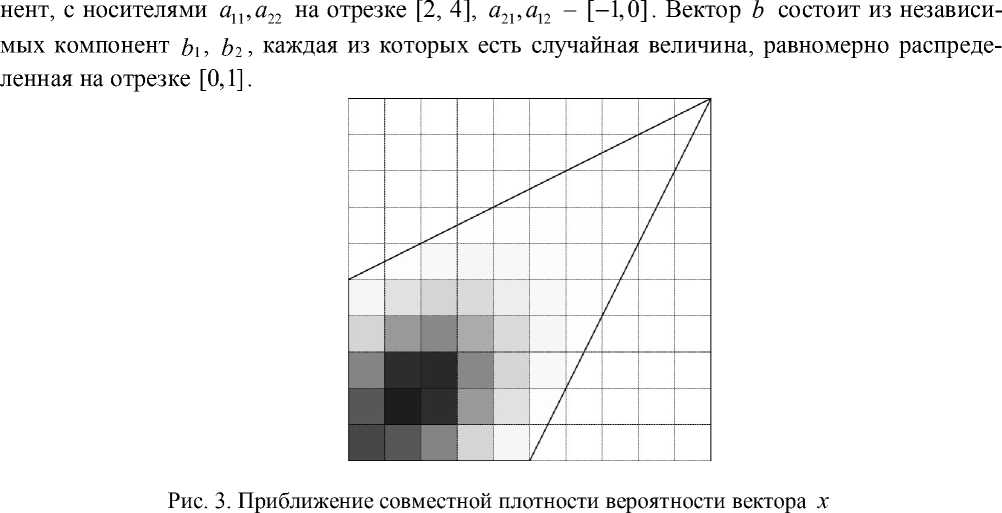
На рисунке 3 приведена кусочно-постоянная аппроксимация совместной плотности вероятности вектора решения х. Сплошной линией проведена граница множества решений ис- ходной системы. Оттенками серого показаны значения функции плотности вероятности. Как видно из приведенного решения, плотность вероятности распределена крайне не равномерно. Есть области, вероятность попадания в которые крайне мала. Все значимые решения сосредоточены в области [0,0.5]2.

Вычисление элементов обратной матрицы. Пусть C = A-1, C = (cij), тогда элемент cu можно представить в виде cii

a 22                   ¹

a il a 22 - a 12 a 21     a il - a 12 a 21

Заметим, что в последнем выражении каждая переменная встречается только один раз и, следовательно, c ₁₁ можно вычислить арифметику над плотностями вероятности.

Прямые методы . В тех случаях, когда нет необходимости вычислять функцию совместной плотности вероятности решения, можно воспользоваться прямыми методами решения.

Используя элементы обратной матрицы, можно вычислить решение ( x₁ , x ₂) системы:

X1 =

; X 2 =

a 22 ^b1 a 12 ^b 2 a 11 a 22 - a 12 ^b 21

a 11 ^b 2    a 21 ^b 1

a 11 a 22 - a 12 b 21

В этом случае для вычисления решения ( x ₁ , x ₂) будем использовать алгоритм 1. Так, для вычисления х ₁ заменим a ₂₂ , a ₁₂ 1 ₂₂ , 1 ₁₂:

x 1 = ZZ P ( 1 22 ) P ( 1 12 ) t ²; ^{6 1} - 1 ¹² b ² .

1 22 I 12                       ^a 11 ¹ 22 t 12 a 21

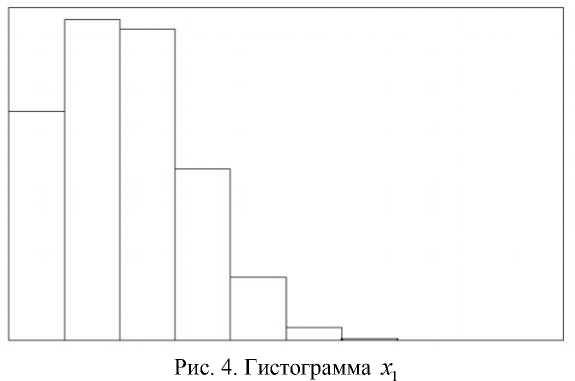
На рисунке 4 приведена гистограмма с шагом h = 0,1 плотности вероятности первой компоненты вектора решения. Носитель х ₁ - отрезок [0, 1], тем не менее вероятность попадания решения в отрезок [0.7, 1] крайне мала.

Заключение

В рамках численного вероятностного анализа построены алгоритмы решения систем линейных алгебраических уравнений с неточными коэффициентами. В тех случаях, когда известны функции плотности вероятности входных данных, построены аппроксимации как совместных плотностей вероятности вектора решений, так и отдельно каждых компонент.