Численное сравнение алгоритмов инициализации следов объектов
Автор: Спивак В.С., Тартаковский А.Г., Беренков Н.Р.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 1 (49) т.13, 2021 года.
Бесплатный доступ
Алгоритмы обнаружения разладки могут быть использованы в большинстве задач инициализации следов объектов. Раньше, когда вычислительная сложность была проблемой, свою популярность завоевал алгоритм K/N благодаря вычислительной легкости. Существенно более эффективный алгоритм инициализации следов может быть построен на основе метода последовательного обнаружения разладки. В данной статье мы рассматриваем алгоритм движущегося среднего. Мы сравниваем характеристики алгоритмов K/N и движущегося среднего. Критерием оптимальности является максимизация вероятности правильного обнаружения в определенном временном интервале при заданном уровне риска ложной тревоги, измеряемом как локальная вероятность ложной тревоги. Для рассматриваемых рабочих характеристик мы получаем теоретическую оценку и оценку методом Монте-Карло. Результаты показывают, что предложенный алгоритм движущегося среднего демонстрирует рабочие характеристики значительно лучшие, чем алгоритм K/N .
Последовательное обнаружение разладки, вероятность правильного обнаружения, локальная вероятность ложной тревоги, алгоритм k/n, алгоритм движущегося среднего
Короткий адрес: https://sciup.org/142229702
IDR: 142229702 | УДК: 519.216.5
Текст научной статьи Численное сравнение алгоритмов инициализации следов объектов
Задача инициализации следов объектов с целвю дальнейшего сопровождения может быть рассмотрена как задача последовательного обнаружения разладки, т. е. обнаружения изменения в наблюдаемом сигнале [1]: интересующий нас объект появляется в неизвестный момент времени, таким образом изменяя свойства наблюдаемого сигнала (процесса). В большинстве задач инициализации следов объектов цель — обнаружить след в определенном временном интервале после появления следа объекта. Таким образом, в качестве оптимального критерия мы выбрали максимизацию минимальной вероятности правильного обнаружения в определенном временном интервале (окне) при ограниченном уровне частоты ложных тревог (срабатываний).
Самым популярным алгоритмом инициализации следов объектов является так называемый алгоритм K/N [2], [3]. Этот алгоритм завоевал свою популярность благодаря своей вычислительной простоте. Во времена, когда вычислительная техника была плохо развита, более сложные алгоритмы не могли быть применимы на практике. Однако, благодаря техническому прогрессу в вычислительной технике, проблема поиска более эффективного алгоритма обнаружения для задачи инициализации следов объектов вновь актуальна и практически важна. К примерам подобных задач относятся инициализация треков спутников, подводных лодок, баллистических ракет и т. д.
В данной работе мы предлагаем в качестве эффективного алгоритма обнаружения алгоритм движущегося среднего (далее ҒМА — Finite Moving Average). В разделе 2 приведена постановка задачи в терминах последовательного обнаружения разладки. В разделе 3 рассматриваются алгоритмы инициализации следов. Здесь приводятся полученные формулы для теоретических оценок рабочих характеристик: в 3.1 для алгоритма K/N , в 3.2 для алгоритма FMA. В разделе 4 представлены результаты симуляций Монте-Карло. Результаты показывают, что алгоритм FMA демонстрирует значительно лучшие рабочие характеристики по сравнению с алгоритмом K/N. Это позволяет нам рекомендовать использовать процедуру FMA на практике для инициализации следов объектов. В разделе 5 представлены выводы по проделанной работе.
2. Постановка задачи
Пусть наблюдаемый процесс {Х„} задается рас пределением Р^. Будем считать, что в неизвестный момент времени v ^v = {0,1, 2,... }) появляется след от интересующего нас объекта. Тогда, после появления следа, наблюдаемый процесс {Х„} задается распределением Рд. Пусть p j ( X ”), j = то, 0 — плотность распределения P j”, г де X ” = (Х1,...,Х„) — выборка размера п. Для фиксированного момента разладки v вероятностное распределение Р , с плотностью р , ( X ”) = p( X ”|v) — является комбинацией до и после изменения плотностей:
р,( X ”) = р Х ) • po( X ”+i X ) =
= П Р-(Хг\ Х г- 1 ) • П Р о (Хг\ Хг -1), г=1 г=,+1
где X ^ = (Хт,..., Хга) и p j (ХП| Х ”-1) — условная плотность Х п, зависящая от X ”-1. Мы считаем, что наблюдение является независимым и одинаково распределенным. Обозначим УД(ж) — плотность в нормальном (до разладки) режиме, и /о(ж) — плотность в режиме после разладки, т. е. в этом случае (1) записывается с р^(Хг| Х г-1) = /ГО(Х^) и р Х X У0(ХД
В данной работе наиболее удачно подходит максиминная постановка, в которой момент разладки v — неизвестное, но не обязательно случайное число.
Любая последовательная процедура обнаружения дает время остановки Т для наблюдаемого процесса. {Х„}.
Как предложено в [4], в максиминной постановке риск, связанный с ложной тревогой, разумно измерять как максимальную локальную вероятность ложной тревоги (LPFA) в определенном окне М , определенную как
LPFA (T) = sup Р^(£ < Т 6 I + М ), (2)
1>0
а риск, связанный с обнаружением, — как минимальную вероятность правильного обнаружения (PD) в определенном окне N, определенную как
PD = inf Pv (v < Т < v + N). (3)
v >0
Однако в задаче инициализации следов объектов разумно задать размеры обоих временных окон М л N одинаковыми N = М .
Для 0 < /3 < 1. пусть С у = {Т : LPFA (T) < 3} — класс процедур обнаружения, для которого локальная вероятность ложной тревоги во временном интервале фиксированной длины N > 1 не превосходит заданного уровня /3- В максиминной постановке цель — найти оптимальную процедуру, которая максимизирует в классе С у вероятность правильного обнаружения (3) во временном интервале фиксированной длины N > 1.
3. Процедуры обнаружения
Обозначим «Hk : v = к» и «Н^ : v = то» — гипотезы, что разладка (появление следа от наблюдаемого объекта) происходит в момент времени 0 6 к < то, и что разладка не происходит никогда (т. е. объект не появляется никогда) соответственно. Тогда, используя (1), мы получаем отношение правдоподобия между этими гипотезами для выборки х п = №,...,хп)
рк ( X ") р_( Х к ) • ро( Х £+1 Х )
Қп р^( Х ") р^( Х ")
= П-=1 р- у | x i-1) • ПГ=М1 р о( Х і | х і- 1 ) =
ПГ=1 р. ( у , х ^ .
"
= п i=k+1
р о (Х і \ Хі - 1 ) р. X X ) ’
к < п.
Так как наблюдения являются независимыми и одинаково распределенными, а р х ( Х,| X г 1 ) = J^(X i ) 11 ро(Хг| Х і-1) = /о(Хг). тогда
"
LRk ,„ = П
і=к+1
/о(Хг)
/^(Хі) ’
к < п.
Обозначим L i = / о ( Х і ) // ^, (Xi).
В качестве наблюдения рассматривается гауссовская модель:
Х г = Ө1ф^} + ^ г , г > 1,
где {€i}{i>1} — нормальная (гауссовская) N" (0, и2) независимая и одинаково распределенная последовательность, Ө > 0, т.е. мы имеем изменение в среднем независимой и одинаково распределенной гауссовской последовательности. Здесь и далее 1в — индикатор события В. В случае гауссовской модели наблюдений отношение правдоподобия
Li =eXP<(u2 Xi 2^2} .
3.1. Алгоритм K/N
Мы рассматриваем алгоритм инициализации следов объектов K/N . На каждом последовательном скане принимается решение о наличии объекта. Для принятия решения на каждом скане мы сравниваем отношение правдоподобия Д из (5) с порогом. Если порог превышен, то ставится отметка о наличии объекта. Если на N последовательных сканах не менее K отметок (обнаружений) о наличии объекта, то след интересующего объекта инициализируется. В противном случае окно смещается последовательно на один скан, и процедура повторяется. Так как Ln(X i ) монотонно возрастает по Хг, мы можем принимать решение о наличии объекта, сравнивая наблюдение Хг из (4) с порогом Һ;
{ 1, если Хг > Һ, 0, если Хг< Һ.
Тогда, время остановки алгоритма K/N'.
n
TK / N = inf n > N
£ U i > K .
i=n — N +1
Чтобы подобрать оптимальный порог, мы можем рассматривать задачу инициализации следов объектов как схему испытаний Бернулли [5], в которой «успех» и «неудача» (обнаружение или не обнаружение на каждом последовательном скане соответственно) определяются вероятностями 5(j)(1) и ду)(0) соответственно:
9ф(0) = 1 -д0-)(1) = Ф ^-^У j = 0,1, (7)
где Ф ^ - ^ ^ , j = 0,1, является функцией распределения гауссовской случайной величины:
Ф ( ) =2 И (^)] , j=0,1-
Таким образом, получена зависимость вероятности обнаружения на каждом последовательном скане от порога и параметров наблюдаемого сигнала.
Вероятность ровно K успехов в N последовательных испытаниях Бернулли pN = cN рк (1 - p)N-к , где CK — биномиальный коэффициент, ар— вероятность «успеха» в каждом последовательном испытании Бернулли.
Тогда, используя (7), мы можем получить рабочие характеристики алгоритма K/N в окне [1, N]:
N
LPFA N = £ C Ngy^N - (0), (8)
z=K
и
N
PD N = £ C N Э^Э^ (0). (9)
z=K
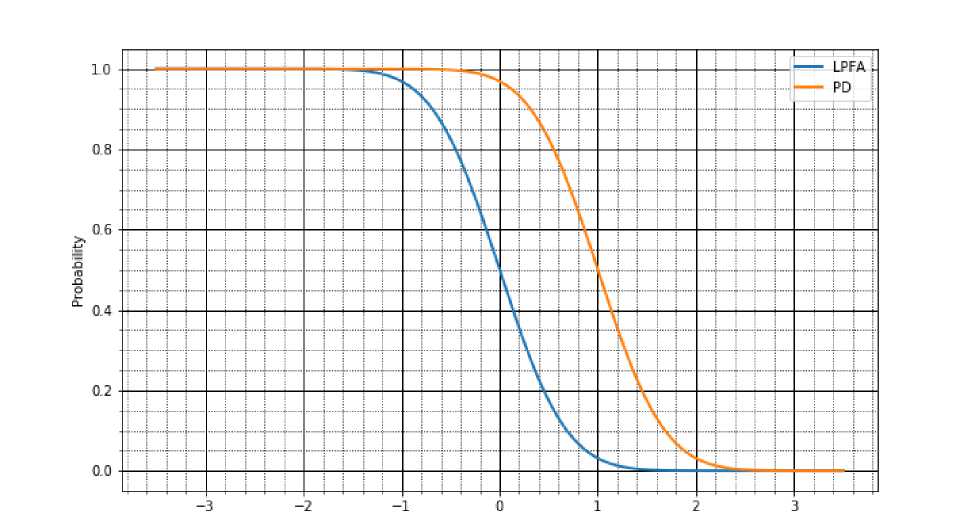
На рис. 1 представлен пример зависимости рабочих характеристик (LPFA и PD) алгоритма. K/N от порога для Ө = 1.
Threshold
Рис. 1. Зависимость LPFA и PD от порога для алгоритма K/N
3.2. Алгоритм движущегося среднего
Для сравнения мы предлагаем алгоритм FMA, который основан на методе последовательного обнаружения разладки. В окне фиксированной длины N считается логарифмическое отношение правдоподобия и суммируется по N последовательным сканам и сравнивается с порогом А. Если порог превышен, то принимается решение об инициализации следа интересующего нас объекта. В противном случае окно смещается последовательно на один скан, и процедура повторяется. Таким образом, алгоритм FMA не что иное, как время остановки
п
Т ^ МА = inf n > N :
У log(A) > А i=n - N +1
Как и в разделе 3.1, мы можем получить теоретическую оценку рабочих характеристик алгоритма. FMA в окне [1, N].
В гауссовском случае сумма логарифмических отношений правдоподобия в окне [1, N]:
A i,n =
N
Е X i i=1
^^^^^^^^r
'2 N. 2a2
(И)
Так как У (N ) = ^Ni X i — гауссовская случайная величина N(N • ', N • a2), то, используя данное свойство гауссовского распределения и (11), мы получаем теоретическую оценку рабочих характеристик алгоритма FMA в окне [1,N]:
LPFA™ 1 (^^N^4 )], М
И
-I Г /N52 _ а\"
PD N MA ..-'Л <13>
Threshold
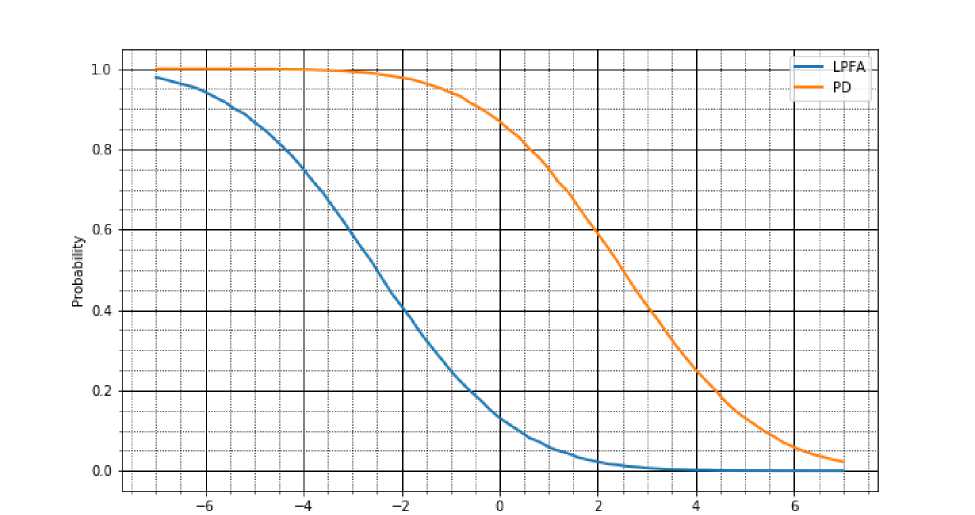
Рис. 2. Зависимость LPFA и PD от порога, для алгоритма. FMA
Таким образом, и для алгоритма. FMA получена, зависимость характеристик обнаружения в зависимости от порога, и параметров наблюдаемого сигнала.
На рис. 2 представлен пример подобной зависимости рабочих характеристик (LPFA и PD) алгоритма FMA от порога для Ө = 1.
4. Численное сравнение алгоритма K/N и алгоритма движущегося среднего
В этом разделе сравним рабочие характеристики (LPFA and PD) алгоритмов K/N и FMA, используя метод Монте-Карло. Минимум в (3) достигается при v = 0. Максимум в (2) достигается при I = N — 1. Однако мы заинтересованы в первую очередь в том, чтобы LPFA не превышала за данный уровень /3, и LPFA^/y ~ LPFAp^^. Поэтому, для простоты, мы будем считать LPFA в окне [1, N].
4.1. Параметры симуляций
1. Мы заинтересованы в низком отношении сигнал-шум (I = Ө"2/2а2. Поэтому мы задаем. Ө = 1: т2 = 1. II в этом случае отіюшешіе спгшгл-шум I = 0.5.
2. Заданный уровень LPFA 3 = 0.2; 0.15; 0.1; 0.05; 0.02; 0.01; 0.001.
3. Результаты симуляций Монте-Карло очень близки к теоретическим оценкам. Поэтому, чтобы получить характеристики, мы подбираем пороги, используя (8), (9), (12), (13).
4. Длина окна N варьируется с 5 до 15.
5. Число прогонов Монте-Карло М = 106, что более чем достаточно, чтобы получить очень точные оценки.
4.2. Моделирование
Моделируем стохастическую модель Хп, используя генератор случайных чисел в (4). Чтобы посчитать LPFA, в каждом прогоне Монте-Карло в наблюдении Х^,п > 1 (г = 1,..., М, М-число прогонов Монте-Карло) мы принимаем, что в (4) v = то. В каждом прогоне Монте-Карло считаем время остановки Т^к и ТрМд, используя (6), (10). Тогда экспериментальная оценка локальной вероятности ложной тревоги сравниваемых алгоритмов:
1 М LPFA = м 52 V^ < n } , г=1
1 М
LPFAPMA = мЕ *{^a Чтобы вычислить PD, в каждом прогоне Монте-Карло в наблюдении А^),п > 1 мы принимаем, что в (4) v = 0. В каждом прогоне Монте-Kaрло считаем время остановки Т^к и ТрМД) используя (6), (10). Тогда экспериментальная оценка вероятности правильного обнаружения сравниваемых алгоритмов: 1 М 1 М PD^ = М ^ ^ Зависимость вероятности правильного обнаружения от локальной вероятности ложной тревоги алгоритмов K/N и ҒМА представлена на рис. 3. Рис. 3. Рабочие характеристики (PD vs. LPFA) алгоритмов инициализации следов объектов: K/N и FMA Таблица 1 показывает результаты сравнения алгоритмов инициализации следов объектов: алгоритм K/N и алгоритм FMA. Видно, что рабочие характеристики алгоритма K/N заметно хуже, чем характеристики алгоритма FMA. Разница тем больше, чем меньше LPFA Таблица! Рабочие характеристики алгоритмов инициализации следов объектов: K/N и ҒМА Уровень /3, ограничивающий LPFA N = 5 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDK/W 0.848 0.800 0.731 0.589 0.418 0.326 0.109 PDfma 0.921 0.886 0.837 0.719 0.571 0.464 0.197 N = 6 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDK/V 0.878 0.833 0.772 0.651 0.493 0.389 0.151 PDfma 0.944 0.917 0.882 0.793 0.658 0.549 0.270 N = 7 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDK/V 0.908 0.876 0.814 0.708 0.543 0.439 0.179 PDfma 0.962 0.948 0.913 0.846 0.727 0.633 0.339 N = 8 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDK/V 0.926 0.901 0.850 0.748 0.600 0.499 0.221 PDfma 0.976 0.964 0.940 0.885 0.782 0.690 0.402 N = 9 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDK/V 0.940 0.917 0.875 0.786 0.659 0.557 0.270 PDfma 0.984 0.975 0.958 0.909 0.825 0.748 0.460 N = 10 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDF V 0.956 0.937 0.904 0.828 0.704 0.600 0.310 PDfma 0.990 0.983 0.969 0.935 0.866 0.795 0.538 N = 11 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDFV 0.966 0.949 0.919 0.855 0.737 0.643 0.351 PDfma 0.993 0.989 0.979 0.951 0.897 0.840 0.595 N = 12 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDFV 0.974 0.963 0.938 0.880 0.783 0.692 0.398 PDFMA 0.995 0.992 0.985 0.963 0.917 0.876 0.646 N = 13 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDC V 0.980 0.970 0.947 0.899 0.809 0.730 0.443 PDfma 0.997 0.995 0.990 0.976 0.940 0.899 0.701 N = 14 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDC V 0.985 0.977 0.958 0.914 0.835 0.759 0.479 PDfma 0.998 0.997 0.993 0.981 0.954 0.922 0.748 N = 15 0.2 0.15 0.1 0.05 0.02 0.01 0.001 PDC V 0.989 0.980 0.965 0.930 0.859 0.787 0.520 PDfma 0.999 0.998 0.995 0.988 0.965 0.939 0.773
5. Заключение Результаты показывают, что предложенная процедура инициализации следов объектов движущегося среднего демонстрирует рабочие характеристики значительно лучшие, чем процедура K/N. Кроме того, симуляции Монте-Карло демонстрируют, что формулы для теоретических оценок рабочих характеристик очень точны. Это позволяет существенно упростить процесс выбора порога для алгоритмов обнаружения. Поэтому мы рекомендуем использовать алгоритм движущегося среднего на практике. Полученные результаты имеют очень важное практическое значение. Работа была поддержана грантом Российского Научного Фонда 18-19-00452 в МФТИ.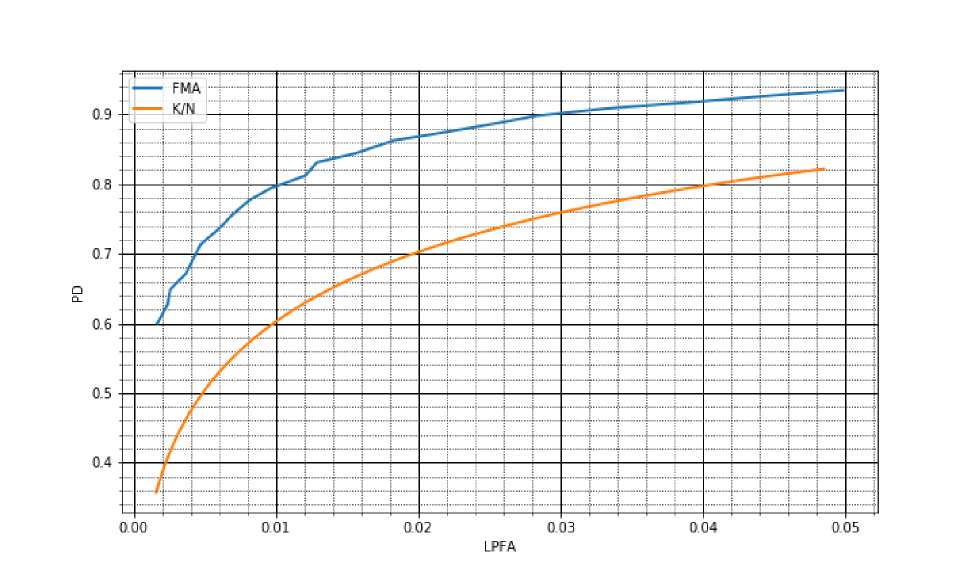
Список литературы Численное сравнение алгоритмов инициализации следов объектов
- Tartakovsky A.G., Nikiforov I.V., Bassevile M. Sequential Analysis Hypothesis Testing and Changepoint Detection/ ser. Monographs on Statistics and Applied Probability. Boca Raton-London-New York: Chapman and Hall/CRC Press, 2014.
- Blackman S.S. Multiple-Target Tracking with Radar Applications, ser. Artech House Radar Library. Dedham, UK: Artech House, 1986.
- Tartakovsky A.G., Brown J. Adaptive Spatial-Temporal Filtering Methods for Clutter Removal and Target Tracking // IEEE Transactions on Aerospace and Electronic Systems. Oct. 2008. V. 44, N 4. P. 1522-1537.
- Tartakovsky A.G. Sequential Change Detection and Hypothesis Testing: General Non-i.i.d. Stochastic Models and Asymptotically Optimal Rules, ser. Monographs on Statistics and Applied Probability 165. Boca Raton, London, New York: Chapman & Hall/CRC Press, 2020.
- Tartakovsky A. G., Veeravalli V.V. Change-Point Detection in Multichannel and Distributed Systems, ser. Statistics: a Series of Textbooks and Monographs. New York, USA, 2004. V. 173. P. 339-370.


