Численное сравнение наиболее популярных быстрых процедур обнаружения разладки
Автор: Спивак В.С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 2 (46) т.12, 2020 года.
Бесплатный доступ
Проводится исследование проблемы последовательного обнаружения момента изменения свойств случайного процесса, встречающейся в различных областях науки и техники. В статье проведен сравнительный анализ трех наиболее популярных процедур: Ширяева, Ширяева-Робертса, кумулятивных сумм (КУСУМ) для задачи с гауссовским наблюдением (сигнал на фоне белого шума). Для этого же наблюдения из интегральных уравнений Фредгольма 2 рода получены характеристики с помощью численного решения интегральных уравнений методом коллокаций. Исследование показало, что в данной постановке задачи наиболее популярная на практике процедура КУСУМ работает заметно хуже процедур Ширяева и Ширяева-Робертса.
Обнаружение момента изменения, процедура ширяева, процедура ширяева-робертса, процедура кусум, гауссовское наблюдение, монте-карло, интегральное уравнение фредгольма 2 рода, численное решение
Короткий адрес: https://sciup.org/142229681
IDR: 142229681 | УДК: 519.216.5
Текст научной статьи Численное сравнение наиболее популярных быстрых процедур обнаружения разладки
В данной работе рассматривается задача, последовательного обнаружения момента, изменения свойств случайного процесса, (разладки). До изменения, в нормальном режиме, наблюдается процесс {Хп}, соответствующий распределению Р^. В неизвестный момент времени v V Е Z. = {0,1,2,...}) происходит изменение, после которого наблюдаемый процесс {К,,} соответствует распределению Рд. В последовательной настройке, пока наблюдения соответствуют ожидаемому, необходимо их продолжать. Как только происходит изменение состояния, обнаружить изменение желательно как можно быстрее.
«Московский физико-технический институт (национальный исследовательский университет)», 2020
В большом количестве практических приложений необходимо быстро обнаруживать изменение. Любая политика обнаружения может привести к ложному срабатыванию, то есть определению алгоритмом, что произошло изменение, хотя на самом деле его (изменения) не было. Желание обнаруживать изменение быстрее приводит к увеличению частоты ложных срабатываний. С другой стороны, желание уменьшить количество ложных срабатываний приводит к большой задержке в обнаружении. Пример решения задачи о разладке представлен ниже: на рис. 1.
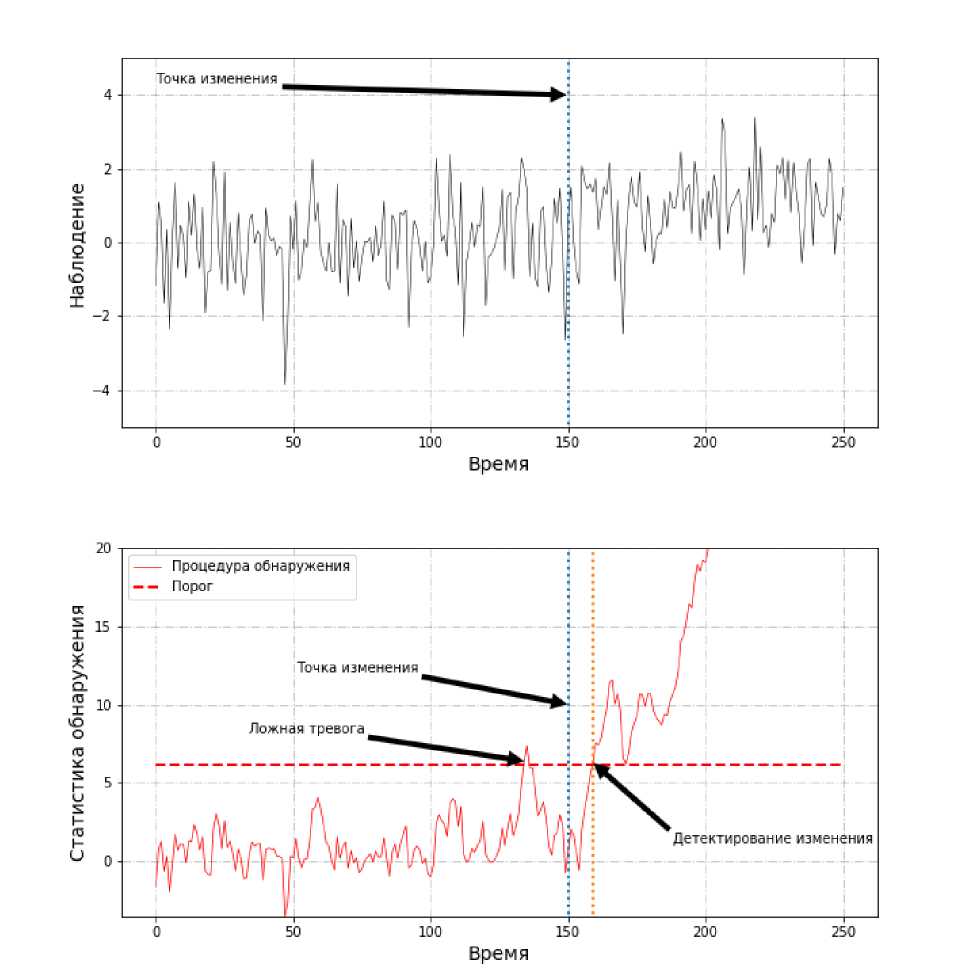
Рис. 1. Пример задачи о разладке
В данной статье мы предоставляем численное сравнение популярных процедур обнаружения: Ширяева, Ширяева-Робертса и КУСУМ в байесовской постановке задачи (момент изменения — случайная величина). Также численно решены интегральные уравнения, позволяющие найти интересующие характеристики и сравнить их с аналогичными, полученными методом Монте-Карло.
2. Модель
Пусть pj (X”), j = то, 0 — плотность распределения Р”, где X” = (Х1 , . ..,Х„) - выборка размера п. Для фиксированного v Е Z+, вероятноетная мера Р^ имеет плотность pv(Xn) = p(X”|v), которая является произведением плотностей до и после изменения:
pv (Xй) = >. X ) • po(X”+i|Xv) =
= П Р-(Хг Х-1) • П ХХ i=1 i=v+1
где Х^ = (Хт,..., Х” ) и pj (Х„|Х”-1) — условная плотность Хп, если задано X”-1. В дальнейшем будем считать, что v — порядковый номер последнего наблюдения перед изменением.
В частном случае, когда наблюдения являются независимыми и одинаково распределенными случайными величинами с плотностями /го(ж) — в нормальном состоянии (до изменения) п /о(ж) — при аномалии (после измепешія). В этом случае в (1) p^(X,■|X' 1) = /Д(ХД а Po(Xi|Xi-1) = / о ( Х і).
В данной задаче мы заинтересованы в байесовской постановке, когда момент изменения — случайная величина, независимая от наблюдений, с априорным распределением вероятности лк = P(v = k), k = 0,1, 2,.... В симуляции будем считать, что априорное распределение является геометрическим:
Р(v < 0) = q іі Р (v = k) = (1 — q)p(1 — p)k д.тя k = 0,1, 2,..., (2)
где 0 6 q < 1.0 < p < 1.
Любая процедура обнаружения момента изменения представляет собой время остановки для наблюдаемого процесса {Х„} Т, являющееся случайной величиной, зависящей от X”. Когда Т 6 v, говорят, что произошла ложная тревога. Хорошая процедура обнаружения гарантирует при отсутствии ложной тревоги маленькую задержку в обнаружении Т — v (уровень ложной тревоги низкий).
Пусть Рк и Е^ — вероятность и соответствующее ей ожидание момента изменения v = k Е Zy. В дальнейшем, Р" обозначим вероятность, определенную как Р"(Л) = 52^=0 лк Рк (Л), и Е" обозначает ожидайие по отношению к Р".
В байесовской постановке рассматриваются риск, связанный с задержкой обнаружения, измеряется средней задержкой обнаружения:
ADD(T) = Е"[Т — v|Т > v] =
∞
^^kEk[Т — k|T > k]P^(T > k)
k=0 _______________________________
1 — РҒА(Т)
и риск, связанный с ложной тревогой, определяется взвешенной вероятностью ложной тревоги (РҒА);
∞
РҒА(Т) = Р"(Т 6v) = ^лкР. Т 6 k). (4)
к=1
Для 0 < а < 1 обозначим Са = {Т : РҒА(Т) 6 а} класс процедур обнаружения, для которых взвешенная вероятность ложной тревоги не превосходит а. В байесовской постановке цель — найти оптимальную процедуру, которая минимизирует среднюю задержку обнаружения в классе Са, то есть найти Topt Е Са такое, что
Е" [Topt
— v|Topt >v]= ^inf Е" [Т — v|Т > v].
3. Процедуры обнаружения
Пусть «Нк : ? = к» и «Н^ : и = то» — гипотезы, что изменение происходит в момент 0 6 к < той что изменение никогда не происходит соответственно. Следовательно, отношение правдоподобия между этими гипотезами, где наблюдение ХП = (Х1, ..., ХП):
LR^ =
п
∏︁ i=k+1
Р Х X л.(Xi|Xi-1) ’
к < п.
Обозначив Li = po(Xi|Xi 1)/рго(Хі|Xi 1), получаем взвешенное отношение правдоподобия:
( п п—1 п \
» П Li + Е» П Li . (5)
i=1 к=0 i=k+1 / где П= Li = 1 И.ти s < j. Пусть Ло = q/(1 — q).
Процедура Ширяева
В нашей модели статистика ЛП = ЛП/р получается следующей из (5):
ЛП = у-р П ( 1-р ) + е П ( I—Р ) . к 1 iк
Время остановки процедуры Ширяева.
ТА = inf{п > 1 : ЛП > А}, А > 0, (7)
где А называется порогом.
Далее мы будем предполагать, что Li не зависит от точки изменения к, что всегда верно для случая независимых и одинаково распределенных наблюдений и часто для марковских и скрытых марковских моделей. Из (6) видно, что статистика ЛП удовлетворяет рекурсии
ЛП = (1+ЛП—1) , п > 1, Ag = q/[(1 - q)p].М
1 — p
Согласно лемме 7.2.1 [1],
PFA(Ta) 6 1/(1 +А) для каждого А > q/(1 — q),(9)
следовательно, из (9) получаем выражение для порога
А = Аа = —,(10)
ар что гарантирует Та Е Cq.
Процедура Ширяева Робертса
Для г > 0, (г = g) определим статистику Ширяева-Робертса. RП:
П П П
RП = гП Li + Е IJL i. (И)
i=1 к=1i=k
Аналогично, как было получено рекурсивное выражение для статистики для процедуры Ширяева, получаем из (11) рекурсивное выражение для статистики Ширяева-Робертса:
RП = (1 + RП—1) Lп, п > 1, R0 = г.
Время остановки процедуры Ширяева-Робертса:
Тв = inf{п > 1 : Rrn > В}, В> 0, (13)
где В — порог.
Согласно субмартингальному неравенству Дуба [2], получаем
РҒА(Тв) 6 ' ",
РВ отсюда (14) выражение для порога
В = Ва
(1 - 9)(1 - Р)(1 + :Р) ра
Процедура КУСУМ
Статистика КУСУМ определена как
п
Vn = max I I Li, п > 1.
06k Так как Li не зависит от точки изменения к, то получаем рекурсивное выражение для статистики КУСУМ Vn = max{1, Vn-i}Ln, п > 1, V0 = 1-Время остановки процедуры Тс = inf{п > 1 : Vn>С}, С > 0, где С — порог. II С = В.
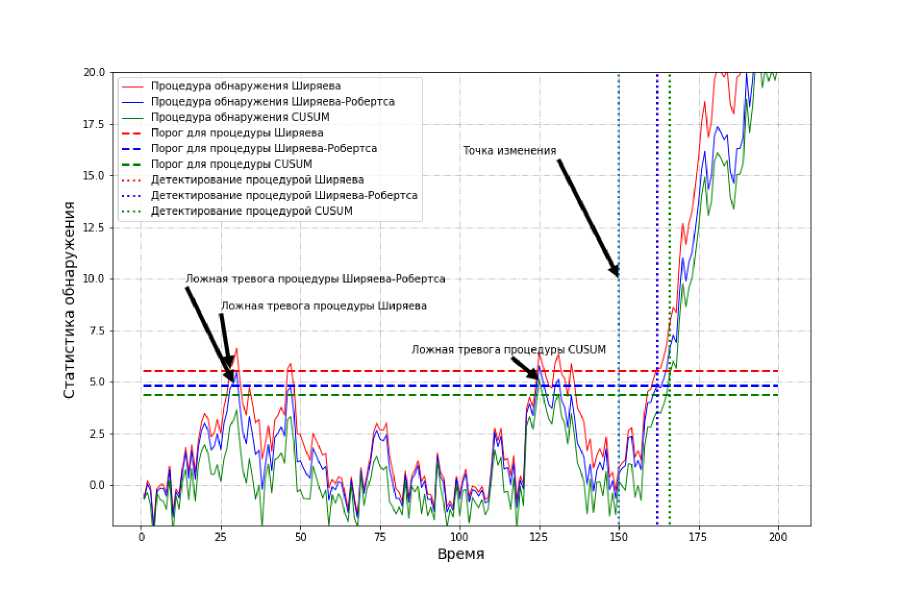
4. Симуляция Монте-Карло для модели гауссовского наблюдения В данной работе, для получения характеристик средней задержки и частоты ложных срабатываний, производятся симуляции Монте-Карло. Момент изменения v получается из геометрического распределения (2). Наблюдение Хп соответствует гауссову распределению с Ы(0,ст2) до точки изменения п с Ы(0, ст2) после Хп = 01{п>,} + ^п, п > 1,(18) Используя генератор случайных чисел, мы получаем наблюдения для каждого прогона Монте-Карло Хп),п > 1 (г = 1,...,N, N — номер прогона Монте-Карло) согласно (18). Отношение правдоподобия, используемое в (8), (12), (16) в данном случае: Ln = exp| Д2Хп - 2^2/- Отношение сигнал-шум определяется как I = 02/2ст2. Для каждой симуляции Монте-Карло из (7), (13), (17) считается время остановки Тд), (І)^(І) ТВ , и ТС для 3 различных процедур: Ширяева, Ширяева-Робертса и КУСУМ, соответ- (І) ственно. Для каждого прогона ложная тревога, то есть ТД < Vi, используется для подсчета вероятности ложной тревоги (из (4)) РҒА(Тд) N -"-^ ~ РҒА(Тв) РҒА(Тс) N N N ^ 1^{Т«<сг}’ i=1 N ^ 1^{^Т«<сг}’ i=1 N ^ Я{тДг)<Ш-i=1 После чего делается оценка Монте-Карло средней задержки обнаружения (из (3)) 1 N1 [№) — ^ [(^- ^-o. р—,.' N т* 1 /^’(.) add(Ts ) = - у <тв — ^я,^^,1 - — (тв ). 1 N 1 (.р^ add(tc) - - |Jtc- ^^} ——ту ■ Число прогонов Монте-Карло — — ^, г де А — это то чность, а а — ограничение для частоты возникновения ложных тревог. Ниже, на рис. 2 показан принцип работы процедур обнаружения для соответствующего наблюдения в логарифмическом масштабе. Время 20 0 17.5 15 0 12.5 10 0 7.5 Точка изменения Ложная тревога процедуры Ширяева-Робертса Ложная тревога процедуры Ширяева Ложная тревога процедуры CUSUM --- Процедура обнаружения Ширяева --- Процедура обнаружения Ширяева-Робертса --- Процедура обнаружения CUSUM — — Порог для процедуры Ширяева — — Порог для процедуры Ширяева-Робертса - - Порог для процедуры CUSUM • • • • Детектирование процедурой Ширяева • • • • Детектирование процедурой Ширяева-Робертса • • • • Детектирование процедурой CUSUM Рис. 2. Пример задачи о разладке 5. Определение харктеристик процедур обнаружения гауссовского наблюдения
5.1. Получение интегральных соотношений Основными характеристиками процедур обнаружения в байесовской постановке являются средняя задержка обнаружения (ADD) и вероятноств ложной тревоги (PFA). Существуют способы определения обоих величин для различных процедур, в первую очередь, как функций порога. Ниже приведены численные методы для решения интегральных уравнений, полученных для перечисленных выше характеристик. Ранее упомянутые определния времени остановки удовлетворяют общему определению: т/ = inf{п > 1 : Rrn > А}, А > 0, r; = Ф(яп-1 )^n, п > 1, r = г > 0, Ф(R) — положительная функция. В частности из (7), (13), (17), для процедур Ширяева, Ширяева-Робертса и CUSUM Ф(R) = (1 + R)/(1 - p), Ф(R) = 1 + R, Ф(R) = max{1,R} соответственно. Тартаковским и Мустакидисом были получены интегральные уравнения для интересующих нас характеристик [3]. Для к > 0 пусть 6к(г) = Ек[(т/ — к)+] и pk(г) = Р^(т/ > к). Тогда вероятность ложной тревоги есть ∞ РҒА(тД) = (1 — g)(1 — р £(1 — p)kрк(г)). (19) к=0 Аналогично для числителя N(т/) и знаменателя Е(тА) для средней задержки обнаружения (АЕВ(т'д) ∞ N(т/) = q^) + (1 — q)p ^(1 — p)k5к(г); (20) к=0 ∞ D^/) = q +(1 — q)p £(1 — p)kрк (г). (21) к=0 Необходимо найти оценки для рядов ∞ Мт) = ^(1 — p)k6k(г)), к=0 ∞ Ар(г) = ^(1 — p)k pk(г), к=0 а также для средней длины пробега до обнаружения 6о- Используя Марковские свойства статистики, Тартаковский и Мустакидис получили следующие интегральные уравнения: 6о(г) = 1 + А У 6о(х) ^(фА ------- ах ох ^р(г) = 6о(г) + (1 — p) '„, ^Л№~Ф^'к, I ^р(х) дх ах, Хр(г) = 1 + <1 — p) / *><х)д^ х dx. Используя решения уравнений (22), (23), (24), легко найти интересующие нас характеристики, подставив в (19) (20) и (21): PFAM) = (1 - q)(1 - рх»), ДПП/ п _ q'VT) ■ п qipryri ( А) q + (1 — q)pXP(r) ‘ Численные решения интегральных уравнений Полученные в предыдущем разделе уравнения (22), (23), (24) являются интегральными уравнениями Фредгольма второго рода. Так как большинство ядер, встречающихся в последовательном анализе, являются плохими, невозможно получить аналитическое решение. Однако существует много численных методов решений, один из которых метод коллокаций [4], который был применён Полунченко к решению некоторых задач [5]. Численные методы позволяют решить эти уравнения с достаточно хорошей точностью. Уравнения (22), (23), (24) заменяются на линейные 8n = 1 + Ko5n ,(27) —n = §n + (1 - pW^—N,(28) Xn = 1 + (1 - p)K^xn,(29) где ядро Кд, d = 0, от — матрица размера N на N, каждый элемент которой Кі’і Р ^< < ф(г-)) Р ^< < ф(-.) )’z,j 1’ 2,-,N, где Р — это функция распределения нормального распределения. Согласно методу коллокаций используется разбиение х, = jA/N, а т = (х. + х.—і)/2,г, j = 1, 2,...,N. Решив линейные уравнения (27), (28), (29), можно найти интересующие значения функций 8n,—n’Xn, нужных нам для отыскания интересующих нас характеристик: N ^n(т) = ^б^ • Cj(r), (30) j=i е,(0 = {(’ т е l9j-i;"'" <31> Аналогично (30) и (31) находим —n и xn- После по формулам (25) и (26) находим вероятность ложной тревоги (PFA) и среднюю задержку обнаружения (ADD). В таблицах с результатами средняя задержка обнаружения и вероятность ложной тревоги, полученные численным решением интегральных уравнений, обозначены как ADDnum II PFAnum- 5.2. Результаты компьютерного моделирования Параметры симуляций. 1) Среднее после разладки Ө = 0.2, 0.4, 0.6, 0.8,1. 2) Параметры геометрического распределения: q = 0; p = 0.5; 0.1; 0.01. 3) Ограничивающая PFA a = 10-1; 10-2. 4) Порог в процедуре Ширяева задается как A = (1 - a)/a, в процедуре Ширяева-Робертса и CUSUM - В = (1 - p)/(pa). Таблицы с результатами Процедура Ширяева Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 2.49 2.48 0.0494 0.0495 0.8 2.67 2.68 0.0560 0.0548 0.6 2.85 2.86 0.0592 0.0601 0.4 2.99 3.00 0.0657 0.0660 0.2 3.08 3.10 0.0716 0.0698 Процедура Ширяева-Робертса Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 2.62 2.58 0.050 0.049 0.8 2.85 2.78 0.057 0.056 0.6 3.06 3.02 0.062 0.059 0.4 3.22 3.14 0.067 0.066 0.2 3.24 3.16 0.069 0.070 Процедура. КУСУМ Ө ADD ADDnum PFA PFAnum 1.0 2.99 2.97 0.048 0.049 0.8 3.37 3.29 0.057 0.056 0.6 3.97 3.93 0.060 0.060 0.4 4.66 4.60 0.066 0.067 0.2 5.94 5.83 0.069 0.070 Таблица 8.1. р = 0.5 и a = 0.1 Процедура Ширяева Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 4.31 4.29 0.00502 0.00505 0.8 4.81 4.79 0.00554 0.00561 0.6 5.31 5.30 0.00619 0.00621 0.4 5.75 5.74 0.00655 0.00683 0.2 6.03 6.03 0.00725 0.00736 Процедура Ширяева-Робертса Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 4.82 4.72 0.00475 0.00489 0.8 5.44 5.38 0.00547 0.00536 0.6 6.30 6.13 0.00612 0.00601 0.4 6.65 6.53 0.00644 0.00635 0.2 6.85 6.76 0.00704 0.00694 Процедура. КУСУМ Ө ADD ADDnum PFA PFAnum 1.0 5.41 5.38 0.00486 0.00485 0.8 6.56 6.59 0.00535 0.00524 0.6 8.12 8.24 0.00594 0.00594 0.4 10.68 10.82 0.00645 0.00641 0.2 14.41 14.78 0.00725 0.00716 Таблица 8.2. р = 0.5 и a = 0.01 Процедура Ширяева Ө ADD ADDnum PFA PFAnum 1.0 5.58 5.57 0.0602 0.0599 0.8 6.91 6.92 0.0696 0.0663 0.6 8.78 8.80 0.0735 0.0739 0.4 11.32 11.34 0.0781 0.0824 0.2 14.12 14.19 0.0920 0.0912 Процедура Ширяева-Робертса Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 5.61 5.60 0.0596 0.0593 0.8 6.84 6.84 0.0713 0.0700 0.6 8.95 8.85 0.0740 0.0750 0.4 11.91 11.80 0.0802 0.0793 0.2 14.99 14.91 0.0875 0.0884 Процедура КУСУМ Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 5.83 5.85 0.0599 0.0594 0.8 7.39 7.30 0.0688 0.0702 0.6 9.84 9.85 0.0755 0.0741 0.4 14.12 14.16 0.0798 0.0789 0.2 21.82 21.93 0.0865 0.0877 Таблица 8.3. р = 0.1 и a = 0.1 Процедура Ширяева Ө ADD ADDnum PFA PFAnum 1.0 9.32 9.32 0.00602 0.00581 0.8 12.18 12.20 0.00650 0.00645 0.6 16.47 16.52 0.00722 0.00723 0.4 23.07 22.99 0.00805 0.00813 0.2 31.03 31.08 0.00919 0.00908 Процедура Ширяева-Робертса Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 9.46 9.50 0.00567 0.00529 0.8 12.72 12.56 0.00628 0.00608 0.6 17.45 17.51 0.00642 0.00649 0.4 25.16 25.19 0.00788 0.00765 0.2 35.45 35.15 0.00901 0.00904 Процедура КУСУМ Ө ADD ADDnum PFA РҒА,, _ г 1 num 1.0 9.69 9.85 0.00562 0.00533 0.8 13.10 13.07 0.00616 0.00626 0.6 18.82 18.83 0.00661 0.00635 0.4 29.34 29.05 0.00792 0.00779 0.2 52.91 52.95 0.00857 0.00856 Таблица 8.4. р = 0.1 и a = 0.01 Процедура Ширяева Ө ADDmc ADDWM PFAmc PFAVLM 1.0 11.41 11.41 0.0589 0.0590 0.8 15.32 15.36 0.0671 0.0653 0.6 21.34 20.44 0.0733 0.0728 0.4 36.62 36.80 0.0829 0.0811 0.2 80.13 79.93 0.0901 0.0902 Процедура Ширяева-Робертса Ө ADDmc ADDVLM PFAmc PFAVLM 1.0 11.45 11.35 0.0596 0.0605 0.8 14.21 14.23 0.0689 0.0680 0.6 21.25 21.22 0.0751 0.0760 0.4 36.54 36.66 0.0797 0.0796 0.2 77.98 77.90 0.0891 0.0887 Процедура КУСУМ Ө ADDmc ADDVLM PFAmc PFAVLM 1.0 11.69 11.68 0.0567 0.0555 0.8 15.47 15.51 0.0669 0.0678 0.6 21.80 21.88 0.0742 0.0743 0.4 38.07 38.15 0.0805 0.0795 0.2 87.64 86.00 0.0881 0.0890 Таблица 8.5. р = 0.01 и a = 0.1
6. Заключение Было проведено сравнение нескольких правил обнаружения, которые имеют оптимальные или близкие к оптимальным свойства при различных критериях качества. Полученные характеристики представлены в табл. 8.1, табл. 8.2, табл. 8.3, табл. 8.4, табл. 8.5. Критерием качества для сравнения служила средняя задержка обнаружения при заданной средней вероятности ложной тревоги, когда правило обнаружения типа Ширяева является оптимальным при условии полностью известного априорного распределения момента разладки, что не является реальным предположением для большинства практических приложений. Было показано, что другая предложенная процедура обнаружения, не использующая априорное распределение, имеет почти такие же характеристики, как и строго оптимальная процедура Ширяева. Также было выявлено, что наиболее популярная процедура КУСУМ, которая почти всегда используется на практике, весьма сильно проигрывает и часто имеет весьма низкие характеристики. Результаты исследования очень полезны для большинства приложений, относящихся к задачам обнаружения случайно появляющихся сигналов от объектов в радиолокационных, сонарных и оптических системах, атак в компьютерных сетях, резких изменений в финансовых структурах, отказов оборудования. Благодарю Тартаковского А.Г. за постановку задачи, помощь и советы, без которых эта работа не была бы выполнена. Работа выполнена в рамках совместного гранта РНФ и Германии: Эффективные методы обнаружения аномалий в больших системах. RSF-DFG.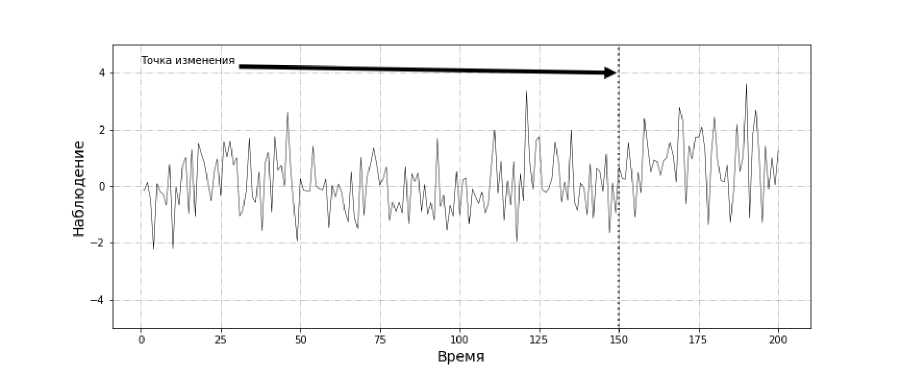
Список литературы Численное сравнение наиболее популярных быстрых процедур обнаружения разладки
- Tartakovsky A.G., Nikiforov I.V., Bassevile M. Sequential Analisis Hypothesis Testing and Changepoint Detection. Ser. Monographs on Statistics and Applied Probability. Boca Raton-London-New York: Chapman and Hall/CRC Press, 2014.
- Tartakovsky A.G. On asymptotic optimality in sequential changepoint detection: Non-idd case // IEEE Transactions on Information Theory. 2017. V. 63, N 6. P. 3433-3450.
- Tartakovsky A.G., Moustakides G.V. State-of-the-Art in Bayesian Changepoint Detection // Sequential Analysis. 2010. V. 29, N 2. P. 125-145.
- Petrovskii I.G. Lectures on the Theory of Integral Equetions. Graylock Press. Baltimore. MD, 1996.
- Polunchenko A.S. Quickest change detection with applications to distributed Multi-Sensor Systems. Dissertation. 2009
- Blanding W.R., Willet P.K., Bar-Shalom Y. Multisensor track management for targets with fluctuating SNR // IEEE Trans. on Aerospace and Electronic Systems. 2009. V. 45, N 4. P. 1275-1292.


