Численные исследования нестационарных процессов при запуске ракетного двигателя

и условной (без учета нестационарных эффектов) тяги РД

R = f ( p U + Д P a ) dF .

Fa

(здесь dF_a – элемент площади среза r_a , ∆ p_a и U_a – плотность, избыточное давление и осевая проекция скорости газа на срезе). На рис. 3 приводятся графики избыточного давления в численных датчиках 1 и 2 на наружной поверхности сопла у среза и на днище РКН – см. рис. 1, а .

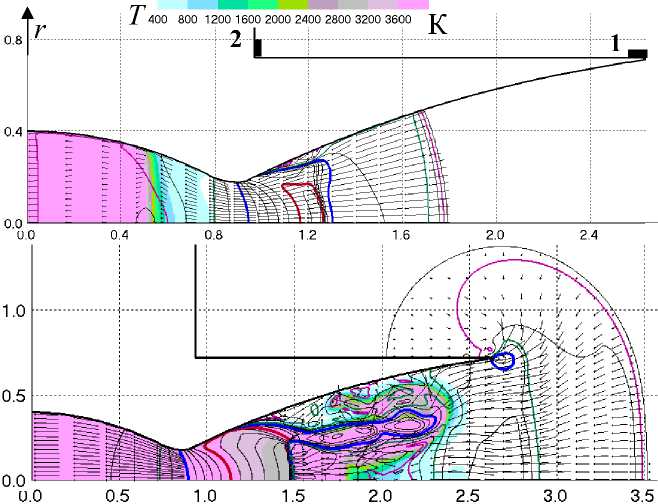
Повышение давления в КС вызывает распространение волн сжатия в сторону среза и одновременно повышение скорости (по мере прохождения пусковых волн). Вначале течение во всем сопле дозвуковое, сопло заполнено холодным воздухом. По мере прохождения пусковых волн скорость увеличивается, и в какой-то момент в критическом сечении сопла она становится звуковой. После этого в расширяющейся части сопла воздух начинает разгоняться до сверхзвуковой скорости (с одновременным падением давления при расширении). Воздух, прошедший критическое сечение раньше этого момента, течет в сопле еще с дозвуковой скоростью. Сверхзвуковое течение догоняет дозвуковое, что приводит к образованию между сверхзвуковым и дозвуковым потоками скачка уплотнения. На рис. 1, а видно, что первичная ударная волна достигла середины расширяющейся части сопла. Давление за ней поднялось до 1,21 кг/см² (здесь и ниже в расчетной области приводятся значения избыточных давлений). Максимальное число Маха в пока еще холодной струе достигло М = 2,3. За критическим сечением струя оторвалась от стенок, что видно из изолинии М = 1,0 (синий цвет) с образованием зоны обратного течения. Течение посредине сопла остается безотрывным.

На рис. 1, б показано поле температур в момент времени t = 0,008 с (давление в КС 17,8 ата). Достаточно четко выделяется диск Маха (скачок

а

б

в

г

Т

T                К

r

Δ p -0.2

кг/см ²

-0.05 -0.02 -0.01 -0.002 0.002 0.01

0.02   0.05

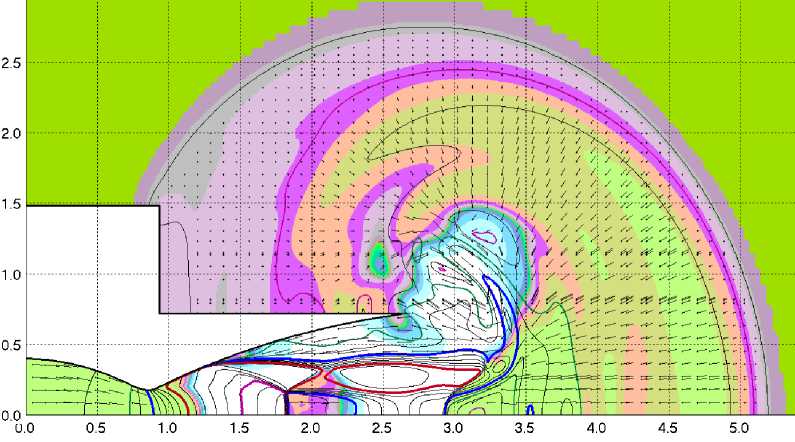
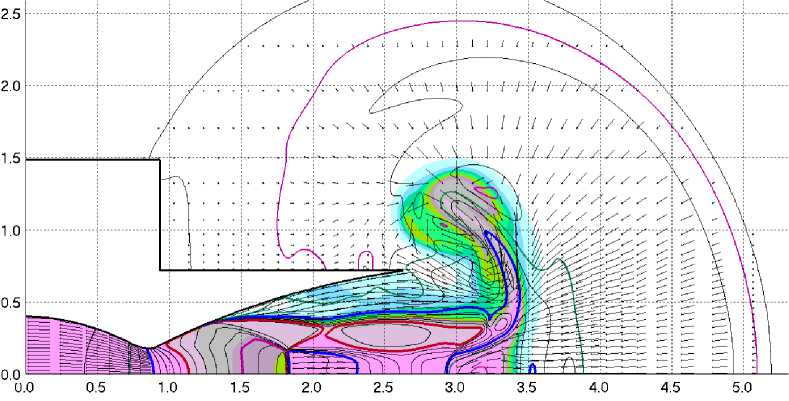
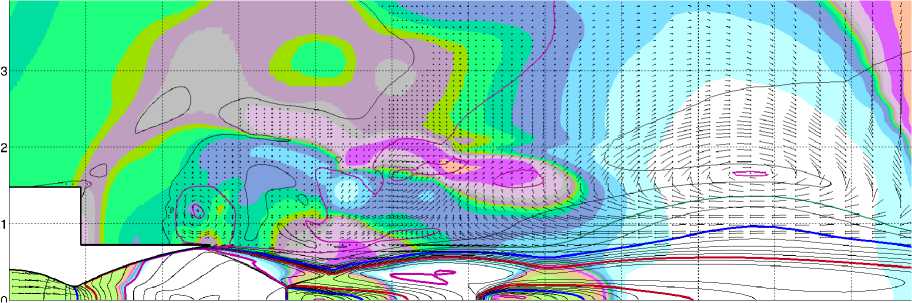
Рис. 1. а–г Вариант 1: а–в – поля температуры для t = 0,004 c, t = 0,008 c и t = 0,012 c, г – поле избыточного давления для t = 0,012 с

Havko____________

Ж ГРАДА уплотнения в приосевой части струи в сечении x - 1,5 м по форме близок к прямому) и отходящие от тройной точки косые скачки. Продукты сгорания прошли через диск Маха и приближаются к срезу сопла, а пакет пусковых волн вышел из сопла. Поток, прошедший через два косых скачка (отходящих от тройной точки), имеет сверхзвуковую скорость и распространяется в виде тонкой кольцевой сверхзвуковой струи (1,5 м ≤ 2,3 м, r - 0,3 м). Данный момент приблизительно соответствует максимумам расхода газа через срез сопла и условной тяги – см. рис. 2. Последующее 106 резкое падение расхода и тяги (в 3–6 раз) связано с уменьшением плотности после того, как через срез начинают истекать высокотемпературные продукты сгорания, а также с затеканием воздуха из внешней среды в циркуляционную область после отрыва потока от стенок сопла.

Пока расход возрастает, фронт первичной ударной волны, вышедшей из сопла, имеет подпитку за счет пакета последующих волн сжатия, что частично компенсирует падение давления на фронте при его сферическом расширении. После падения расхода подпитка прекращается и вслед за волнами сжатия начинают распространяться волны разрежения.

На рис. 1, в показано поле температур, а на рис. 1, г – избыточного статического давления при t = 0,012 с (давление в КС 26,3 ата). Давление на срезе сопла в области отрыва падает до -0,4 кг/см², при этом в районе самой точки отрыва остается еще небольшая область с положительным давлением. И в дальнейшем давление в области отрывного течения существенно изменяется в пространстве и времени.

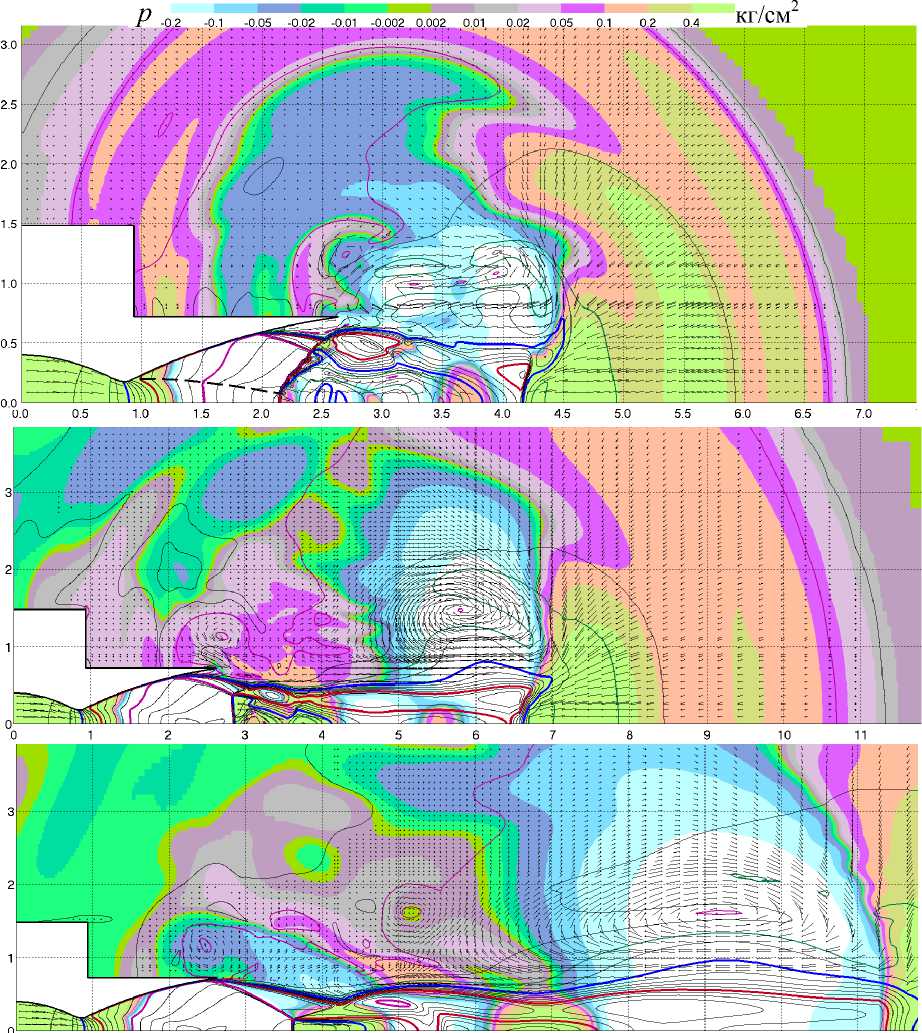
На рис. 1, д показано поле давлений в момент времени t = 0,016 с (давление в КС 34,6 кг/см²). Формы скачков, их положения и положение точки отрыва существенно изменились в сравнении с рис. 1, г . Вместо диска Маха, близкого по форме к прямому скачку, образовался криволинейный скачок, распадающийся в его периферийной части на два косых. Подобный эффект описан в [9]. Это связано с приближением точки пересечения последней (пограничной) характеристики Прандтля-Майера (на рис. 1, д она показана пунктирной линией) со скачком к оси струи. До этой характеристики (между характеристикой и осью) скорости практически не меняются по радиусу; после характеристики – быстро падают по мере увеличения радиуса. Это приводит к образованию новой конфигурации скачка выпуклой формы, причем после перестройки он смещается в сторону критического сечения. На рис. 1, д видно, что скорости газа за скачком в данный момент времени направлены в сторону критического сечения (при этом скорость самого скачка, перемещающегося также в сторону критического сечения, боль-

Том 1

ше скорости газа за ним). Причина связана с тем, что поток, прошедший два косых скачка (на радиусах r ≈ 0,2–0,4 м – см. рис. 1, д ), имеет большее статическое давление, чем полное давление газа, прошедшего прямой скачок в районе оси. Разница давлений оказывается настолько существенной, что газ, текущий в обратном направлении в районе оси, разгоняется до небольших сверхзвуковых скоростей ( x - 2,5 м). Такая конфигурация ударных волн с обратным направлением течения газа в приосевой области за центральным скачком была численно исследована в работе [9]. Показано, что эта конфигурация является неустойчивой и скачок может совершать колебания с определенной частотой, что сопровождается изменением давления в приосевой области. Структура сверхзвуковой струи при этом также постоянно деформируется: изменяет свое положение как граница внутренней дозвуковой зоны, так и наружная граница струи. Изменяется и положение точки отрыва, причем скорость перемещения точки отрыва изменяется в диапазоне от 25 м/c в направлении среза сопла до 10 м/c в противоположном направлении, а обратные перемещения точки отрыва за один полупериод достигают 0,25–0,3 м. Изменение структуры течения сопровождается интенсивным излучением акустических волн, которые накладываются на пусковые волны. Как показано на рис. 1, д , пусковая волна прошла донный срез ракеты. Численный датчик 2 на донном срезе фиксирует максимум давления A p = 0,39 кг/см² при t = 0,0153 с (см. рис. 3). Большое значение максимума объясняется малым временем выхода РД на режим.

Быстрое нарастание и последующее (при t = 0,008 с) быстрое уменьшение расхода через срез сопла в некоторой степени аналогично течению при взрыве. Классический взрыв сопровождается выбросом в пространство большого объема газа, после чего расход резко падает и наступает фаза разрежения. В данной задаче также можно выделить фазу разрежения при t = 0,17–0,24 с – см. рис. 3. На эти процессы накладываются описанные выше пульсации давления. При развитии нестационарной струи образовались мощные пусковые вихри. В процессе перестройки и изменения ударно-волновой структуры струя взаимодействует с этими вихрями, что также оказывает влияние на ее структуру. На рис. 1, е показаны поля статического давления в моменты времени t = 0,027 с (давление в КС 57,7 кг/см²). Повышение давления в камере РД привело к восстановлению традиционной волновой структуры с диском Маха.

На рис. 1, ж–з показаны поля статического давления в моменты времени 0,041 с и 0,043 с (давления в КС 87 кг/см2 и 91 кг/см2). Точка отрыва приближается к срезу сопла. В сечении x = 4,3–4,6 м около границы струи имеются области, в которых происходит быстрое изменение давления, что со- д

е

Havko-

Ж ГРАДА

Том 1

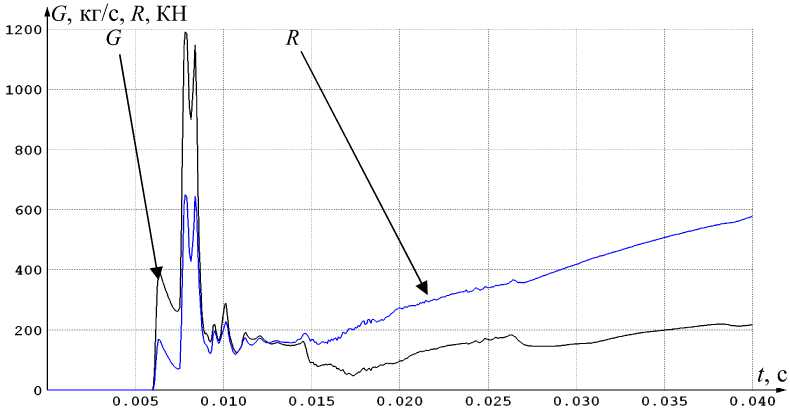
Рис. 2. Вариант 1. Зависимости расхода, условной тяги и давления в КС от времени

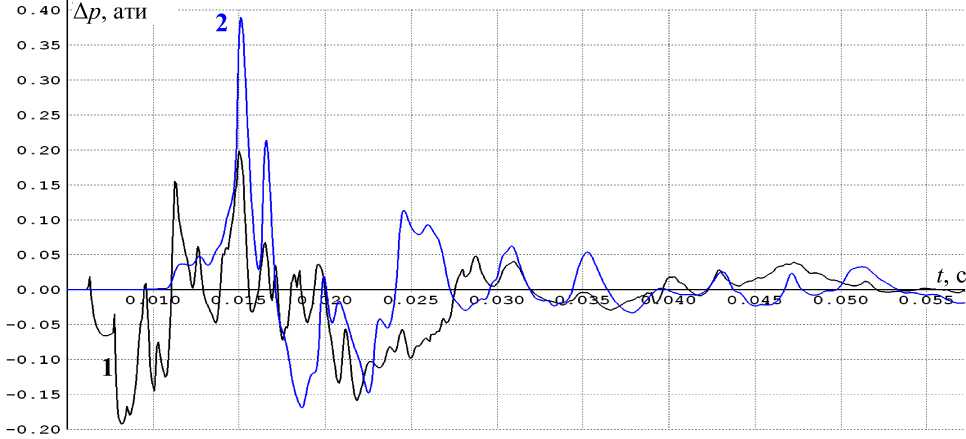
Рис. 3. Вариант 1. Показания численных датчиков давления 1 и 2

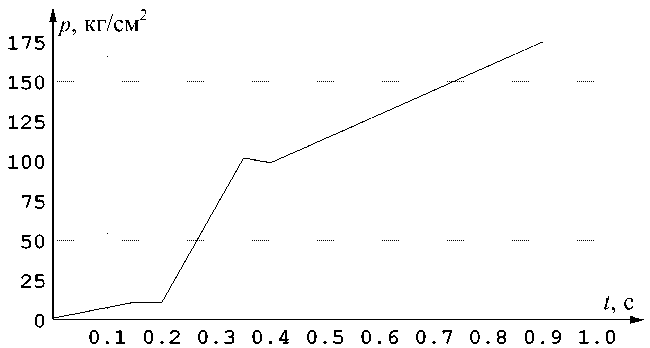
Рис. 4. Вариант 2. Закон изменения давления в КС

провождается излучением акустических волн. На рис. 3 видно, что начиная с t = 0,03 с на днище и срезе сопла наблюдаются колебания, которые, по-видимому, связаны с механизмом Пауэлла. Согласно [1, 10] период таких колебаний определяется по формуле т_п = 1 / с _н + 1 / и к , где 1 - расстояние от среза сопла (в данном случае - от точки отрыва) до источника излучения на границе струи; с _н – скорость звука во внешней среде (воздухе); и к » 0,8 и _экв - скорость распространения возмущений в струе, и экв - скорость эквивалентной изобарической струи с такими же тягой и расходом, что и реальная. В качестве источника излучения обычно принимают границу первой и второй бочки, в которой происходят интенсивные колебания границы струи (сечение x = 4,2 м на рис. 1, ж–з ). Возмущения, дошедшие по воздуху до точки отрыва, вносят возмущения в сверхзвуковую струю (изменяют давление за точкой отрыва и положение самой точки) и далее распространяются по струе. Если принять расстояние от области излучения до точки отрыва 1,5–1,6 м, то пауэлловская частота окажется равной 200-225 Гц. По рис. 3 частоту колебания для 0,03 с <  t < 0,045 c можно оценить как 220–280 Гц.

По мере роста давления в камере размер диска Маха уменьшается и струя становится более устойчивой, поэтому к t = 0,055-0,06 с колебания давления прекращаются.

Далее рассмотрим запуск РД типа РД-191, приняв закон изменения давления в КС подобным реальному - рис. 4 (вариант 2). На рис. 5 приводятся поля избыточного статического давления для этого варианта, на рис. 6 - временные зависимости расхода газа через срез сопла и условной тяги РД, на рис. 7 – графики избыточного давления на днище РКН (см. численный датчик 2 на рис. 1, а ).

На рис. 5, а показано поле статического давления для t = 0,010 с (давление в КС 1,76 ата). Течение в сопле в районе критического сечения – слабое сверхзвуковое. ПВ выходят из сопла, их интенсивность не превышает 0,1 кг/см². Зона отрыва в сопле имеет малую протяженность, в остальной части сопла течение безотрывное. Как показано на рис. 6, расход газа (на первом этапе воздуха) через срез сопла начинается при t = 0,0075 с и достигает максимума при t = 0,0175 с.

На рис. 5, б цветом показано поле давления для t = 0,016 с (давление в КС 2,2 ата). Протяженность зоны отрыва увеличилась, однако в районе среза течение пока безотрывное и истекает холодный воздух. Как видно на рис. 7, давление на днище РКН при достижении фронта ПВ ( t = 0,015 с) не превышает 0,009 кг/см² (в варианте 1 - 0,04 кг/см²). Максимальная скорость в струе соответствует М = 1,2. Давление в области между оторвавшейся струей и стенкой сопла существенно неравномерное.

На рис. 5, в показано поле давления при t = 0,024 с (давление в КС 2,68 ата). К этому времени давление на донном срезе ракеты достигает 0,022 кг/см² - см. рис. 7. При t = 0,03-0,05 с имеет место фаза разрежения, затем ( t = 0,05-0,1 с) колебания, связанные с прохождением пусковых волн, затухают. Далее до t = 0,2 с в расчете регистрируются только высокочастотные колебания с малой амплитудой и частотой около 500 Гц.

Начиная с t = 0,2 с скорость роста давления в КС существенно повышается. На рис. 5, г приведено поле давления для t = 0,202 с (давление в КС 12,8 ата). Как видим, из сопла истекает коль-    109

цевая струя с относительно небольшой скоростью (М < 2,0). При t = 0,214 с точка пересечения последней характеристики Прандтля-Майера с диском Маха приближается к оси сопла (см. пояснение к рис. 1, д ), что приводит к образованию криволинейного скачка, имеющего выпуклую форму, и неустойчивости течения. В качестве иллюстрации такой неустойчивости на рис. 5, д-е приведены поля статического давления для t = 0,231 с и t = 0,233 с (давления в КС 29,8 ата и 31,0 ата). Сравнив их, можно сделать вывод, что за промежуток времени 0,002 с происходит существенное изменение границ струи, границ внутренней дозвуковой зоны, положения криволинейного скачка и точки отрыва струи от сопла. В данном случае мы имеет более сложную, чем в механизме Пауэлла, колебательную систему, в которой реализуются совместные осевые и радиальные колебания. К t = 0,234 с восстанавливается конфигурация с диском Маха, однако колебания продолжаются.

Согласно рис. 7 частота колебаний при t = 0,24-0,28 с оценивается в 100-160 Гц, что согласуется и с измерениями при натурном пуске (120-140 Гц). Отметим, что данная частота существенно ниже пауэлловской. На рис. 5, ж-з показаны поля статического давления при t = 0,261 с и t = 0,269 с (давления в КС 47,9 ата и 49,2 ата). На рисунках видно, что основной источник излучения находится на границе струи в сечении x ~ 3,6. Расчетная (пауэлловская) частота колебаний составляет 190-220 Гц. По-видимому, частота колебаний в данном случае определяется совокупностью более сложных процессов. На колебания могут оказывать влияние нестационарное течение в узкой области отрыва между границей струи и стенкой сопла, неустойчивая область течения за диском Маха (его размеры в данном случае составляют более половины от радиуса струи) и ряд других факторов.

При t = 0,3 с точка отрыва выходит на срез сопла, после чего колебания давления становятся нерегулярными и затухают.

Таким образом, для современных РКН, имеющих растянутую циклограмму выхода РД на режим, при запуске РД можно выделить две харак-

Havko-

ЖГРАДА

Том 1

а

б

кг/см ²

-0.1 -0.05 -0.01 0.01 0.05 0.1    0.2    0.4    0.6

-0.2

р

в

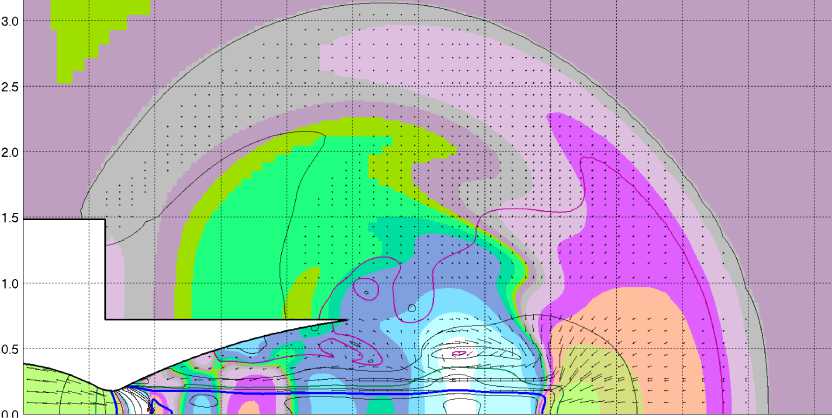
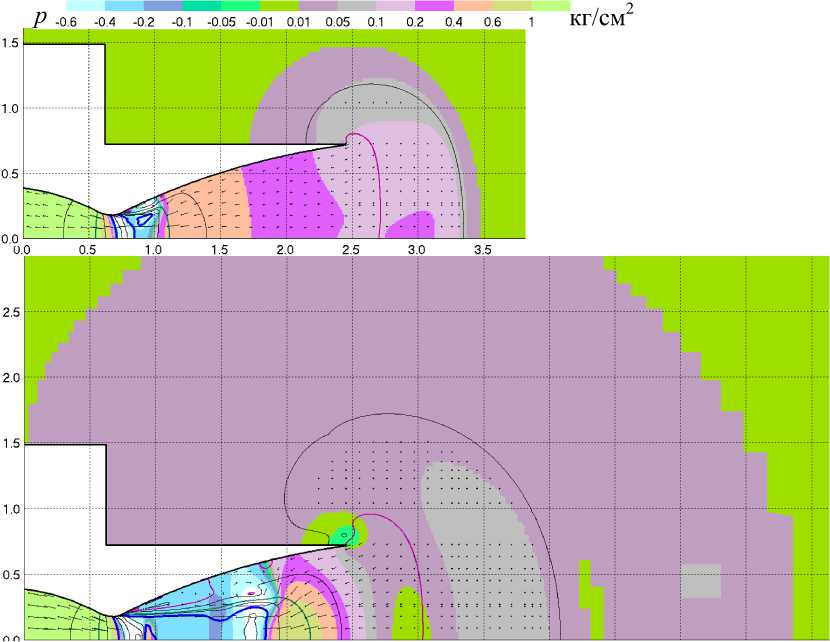
г

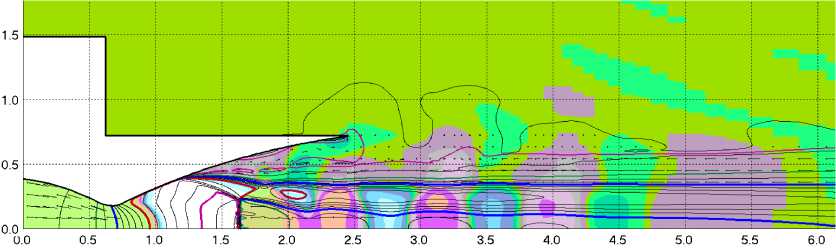
Рис. 5. а-г Вариант 2. Поля избыточного давления для t = 0,01 c, t = 0,016 c, t = 0,024 c и t = 0,202 c

р -0.6 -0.4 -0.2 -0.1 -0.05 -0.01 0.01 0.05 0.1    0.2 0.4 0.6    1 кг/см²

д

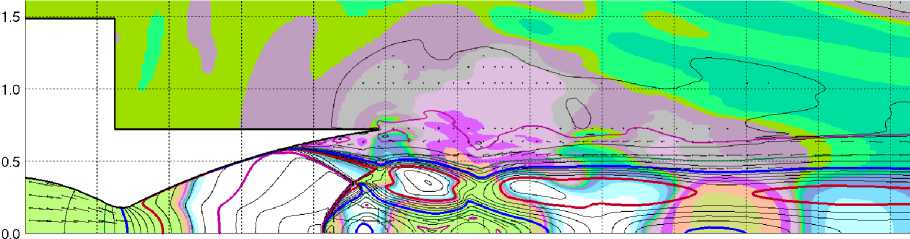
е

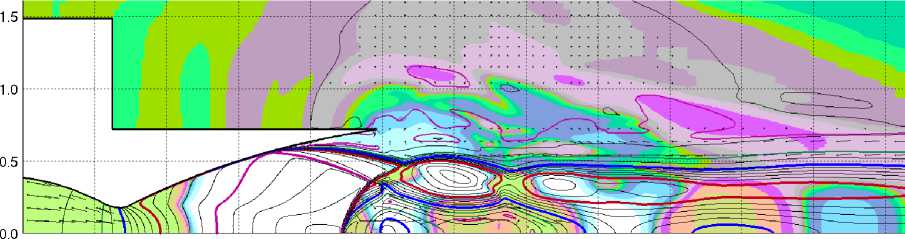
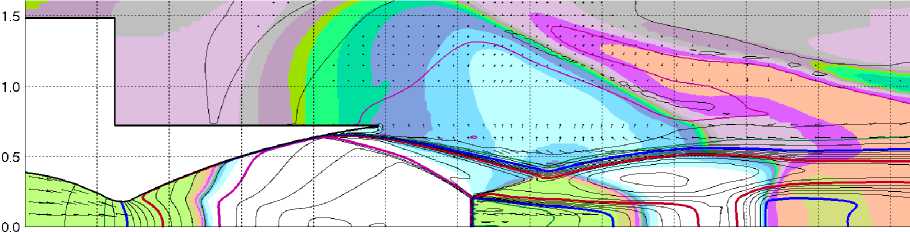
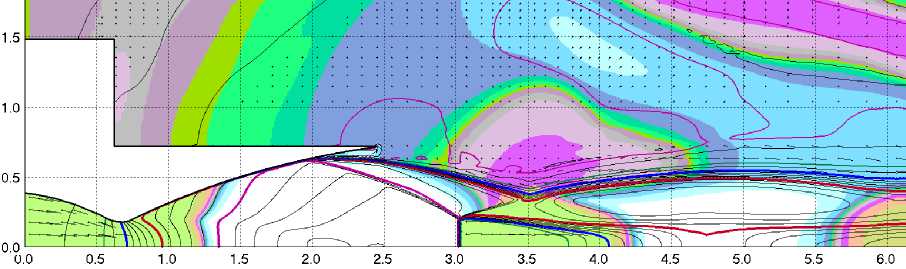
Рис. 5. д-з Вариант 2. Поля избыточного давления для t = 0,231 c, t = 0,233 c, t = 0,261 c и t = 0,269 c

Havko-

Ж ГРАДА

Том 1

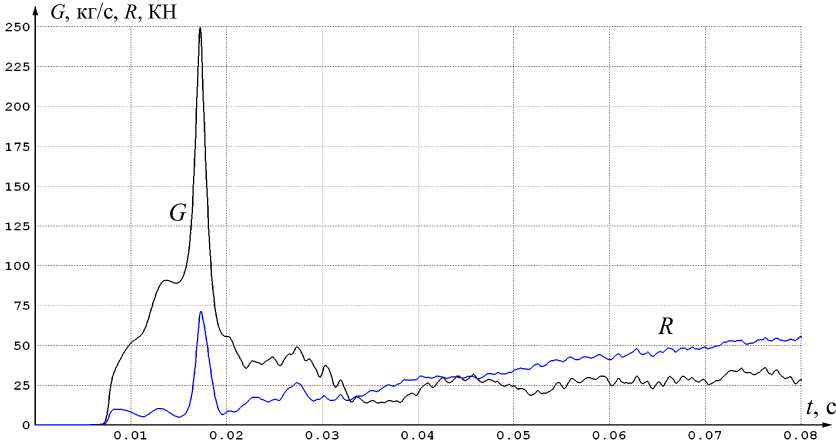
Рис. 6. Вариант 2. Временные зависимости расхода и условной тяги

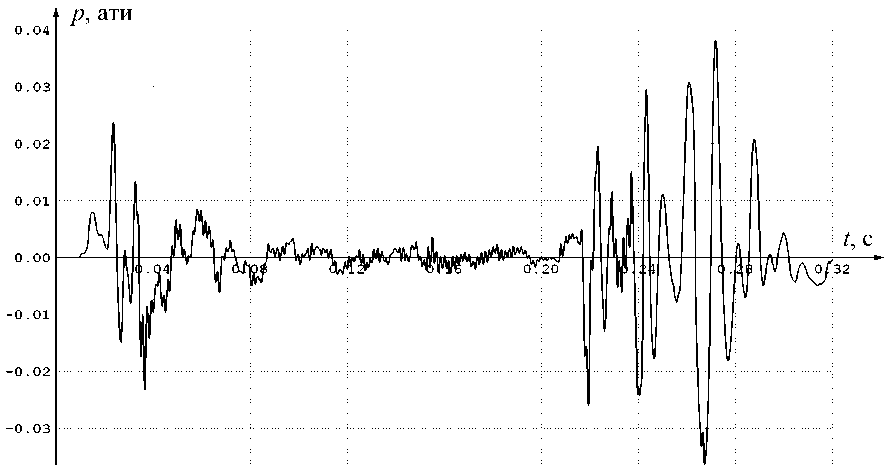
Рис. 7. Вариант 2. Давление на днище РКН (численный датчик 2)

терных фазы волнового воздействия на РКН и ПУ: фазу, связанную с распространением пусковых волн, и фазу пульсационного воздействия. Начало второй фазы определяется приближением точки пересечения последней (пограничной) характеристики течения Прандтля–Майера с диском Маха к оси струи. При этом реальные частоты колеба ний могут оказаться заметно ниже частоты пауэл-ловских колебаний, определенных по длине первой бочки струи. Амплитуда колебаний давления на участке пульсационного воздействия оказывается выше амплитуды пусковых волн. При наличии экрана амплитуда колебаний давления может дополнительно увеличиться.