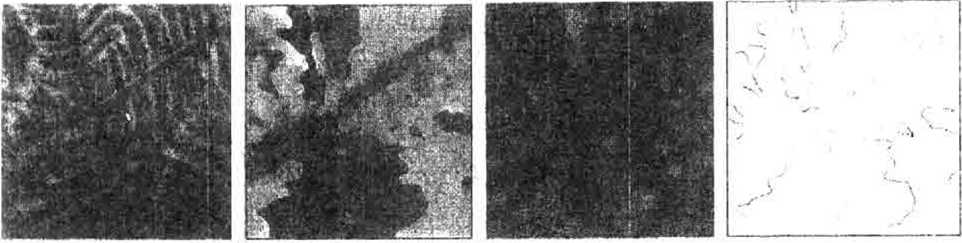
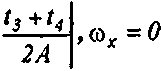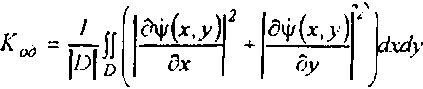Численные методы и алгоритмы построения полей направлений квазипериодических структур
Автор: Ильясова Н.Ю., Устинов А.В., Храмов А.Г.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений: Восстановление изображений, выявление признаков, распознавание образов
Статья в выпуске: 18, 1998 года.
Бесплатный доступ
Описываются новые численные методы построения поля направления, приводится полная классификационная схема методов и алгоритмов построения поля направлений, описание ее классов. Дается сравнительный анализ алгоритмов по точности и быстродействию в отдельных классах, а также между классами указанной схемы. Приводятся примеры практических задач анализа изображений, решаемых с использованием поля направлений (анализ дактилограмм, кристаллограмм биологических сред).
Короткий адрес: https://sciup.org/14058373
IDR: 14058373
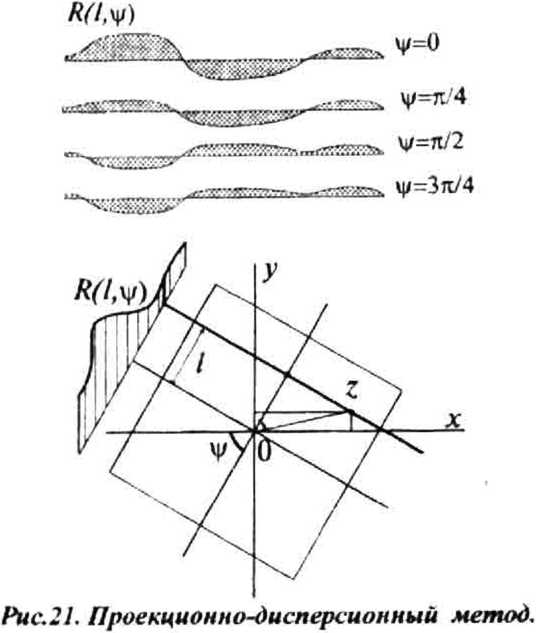
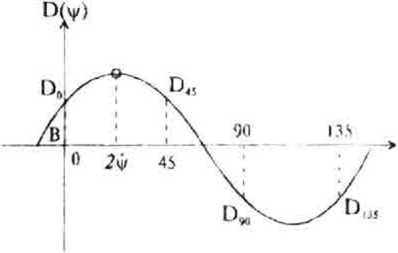
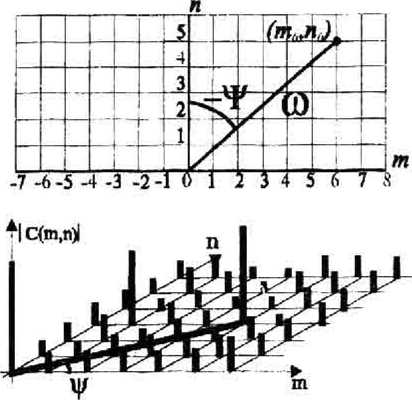
Текст научной статьи Численные методы и алгоритмы построения полей направлений квазипериодических структур
аппроксимация цилиндрической поверхностью: 'a^v4 *6akyu2v2 A-ak4yu4 A-c^v2 +ck2l£u2 = = ^02*2к^пА-к2\х20, b^v2 A-bk2yu2 =p.01A-kp.10, ay,v2 Aak2yu2 A-c^l = ^.(>0, ^
6a2kyu2v2 *2a2k3yu4 *2аскУи2 ^b2kyu2 =
= 2a\xzlA-2ak\x20A-by.10.
/Аппроксимация плоскостью. В системе координат, связанной с положением скользящего окна И7, зададим одномерный полином / (х.у). аппроксимирующий изображение 1(х,у) в виде плоскости: 7(х, у) = ах + by + с,(х, y)eW , коэффициенты которого имеют следующий вид:
М(Ма-1Х2Ма-1) * М (М + 1\2М +1) "
Используя определение поля направлений и систему (2) получим для его определения следующее выражение:
^(х,^) = -ц^/ц0/
Квадратичная аппроксимация. Метод локальной квадратичной аппроксимации основан на аппроксимации функции /(х,у) в пределах окна W квадратичной поверхностью:
/(х.у) = ах2 + by2 + сху A-dxA-eyA- f,(x,y) е W (6)
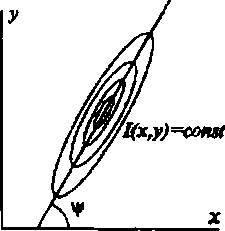
Рис.5. Линии уровня квадратичной поверхности
За значение поля направления в точке (х.у) принимается направление главной оси параболоида (б) (рис.5), когда центр окна W находится в точке (х.у). Численное решение данной задачи приведено в [6], где предложен эффективный алгоритм вычисления коэффициентов с использованием рекучреив-ного метода вычисления моментов (3). Для определения направления главной оси параболоида перейдем к каноническому виду уравнения поверхности [7]:
I^d,y)=dx!2 А-Ь*у2 + /'.
Для этого используем следующие аффинные преобразования координат:
х = x’cosa- у'sina+ x0, , . , .где у = xsma+ у cos a* y0,
ce - 2bd
X0 = ' . 2’
4ab - c ,-.
cd - 2ae
Уо=-"—
4ab - c являются координатами вершины аппроксимирующего параболоида, а угол а определяется из следующего уравнения: tg2a = с /(а - Ь) .
В результате решения данного уравнения получим два взаимно перпендикулярных направления aj и «2, соответствующие главным осям квадратичной поверхности (6). Выбор направления, соответствующего большей полуоси, осуществляется следующим образом: a = arg mwh'L где [“/-“Я а1 = a cos2 а + b sin2 а + с sin а cos а .
Данное выражение получено при переходе к каноническому виду уравнения поверхности с помощью аффинного преобразования координат (7). Вектор параметров аппроксимирующего полинома найдем из системы (4):
а =-----------
М^М+l\2M + У)2 \4М2 +4М-3)
(2М + 1У^4М2 4-4М-ЗУ
М(М + 1\2М + iy\4M2 + 4М~з} (2М + 1У ^4М2 + 4М - })'
с-
М2^+1У^2М-ИУ :
М(М + 1\2М + 1У ’
М<М^1\2М^1У ’
, _ nW -\г 14М -У]- 15{у20^02}
-
3 " ^2М^1У^М2\4М-3^
Цилиндрическая аппроксимация. Общая идея метода предложена в [8]. Мы рассмотрим построение системы нелинейных уравнений в явном виде. В системе координат скользящего окна рассмотрим полином второго порядка одной переменной, который повернут на плоскости изображения на некоторый угол ц/, аппроксимирующий изображение Кх.у) в виде цилиндра 7(х,у) =а(у -ткхУ +b(y +кхУс , где k=-tg у. За направление в центре окна (х,у) принимаем направление, вдоль которого повернут ци-линдр, а именно, угол цл Параметры а, Ь. с, к аппроксимирующего полинома определим из системы (5):
Q = ^^ifcL^JlAlliJz^
^(^ *6ks22 +P$J^ *к2$2У b_ ^02^^10)
-
- МкМ-ИХ2М + 1У^1 + к2У (8)
P-00-°82\14-к2)
с = -------ZA----- I, 6a ks22 + 2a2k3s4 + so
+ 2acks2 +b2ks2 = 2ayin +2aky.2o +^Pw где sM= ZZ^V,
^.y^w s^-Soo = (2A/ + /)2,
MkM + 1\2M 4-1)2
s2 - S20 - s02 - -,
_м2км ^1Ук2М31У
S 22-- .
-
_ мкм + 1\2M + ГУ^ЗМ2 + ЗМ - /)
-
S4 - S40 -S04 -is
В отличие от аппроксимации плоскостью и квадратичной поверхностью система (5) является нелинейной, что требует использования для ее решения соответствующих численных методов.
Метод комбинированной аппроксимации. При проведении исследований рассмотренных методов было замечено, что при аппроксимации изображения плоскостью возникает большая погрешность в точках экстремума функции яркости, а при аппроксимации квадратичной поверхностью - в точках перегиба. Из рис.6 видно, что в точках экстремума функции (участок 1) погрешность можно уменьшить, используя параболическую аппроксимацию, в точках перегиба (участок 2) - аппроксимацию прямой (для двумерного случая - плоскостью). Таким образом, воспользуемся методом комбинированной аппроксимации. Определим две величины, характеризующие соответственно параметр крутизны и кривизны аппроксимируемой функции:
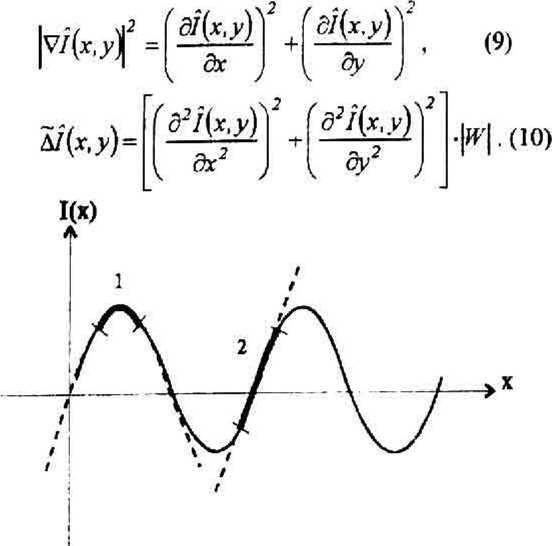
Рис.6. Метод комбинированной аппроксимации
Величина (9) достигает высоких значений в точках перегиба, а величина (Ю) в точках экстремума. Согласно (6) данные характеристики будут иметь следующие выражения: |v/(x,>’)| = d"+e2, М(х,у^ = 4(а2 +b2 )(2М +1 )2 . Использование конкретного способа аппроксимации определяется следующими условиями: аппроксимация плоскостью: |v/(x,y)| >Д7(х,у), параболическая: Iv/(x,y1 <Д/(х,у).



а) б) в) г)
Рис. 7. Иллюстрация работы методов параметрической аппроксимации: а) изображение uнmepфq)oгpaм.чы; поле направлений, полученное методом: б) аппроксимации плоскостью, в) параболической аппроксимации, г) комбинированным.
Экспериментальные исследования. Класс методов локальной параметрической аппроксимации обладает высокой устойчивостью к шумам, так как метод наименьших квадратов имеет шумоподавляющее свойство. Недостатком же является необходимость адаптивного выбора размеров окна обработки IV (размер окна должен быть меньше расстояния между соседними полосами).
Проведем исследование рассмотренных выше методов на тестовых изображениях. Из-за специфики значений отсчетов поля направлений невозможно использовать понятие среднеквадратической ошибки в обычном смысле. Воспользуемся представлением поля направления в комплексной форме (1) с единичной весовой функцией. В данном случае под среднеквадратичной ошибкой будем понимать следующую величину:
~ 1 „I. Т I-7
е = pj JJ |^(х,у; - х, dxdy, где D - область изображения. у(х,у)- истинное значение поля направления, ф(х,у) - его оценка. Используя (1), получим:

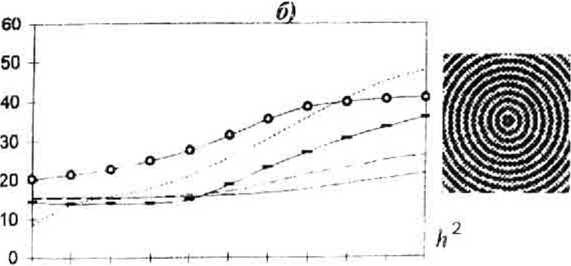
Рис.8. Тестовые изображения квазипериодических структур: а) с константным
б)-г) различные виды
полем направления;
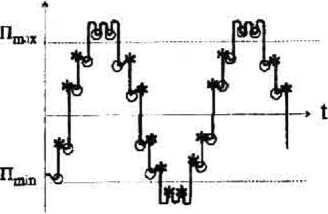
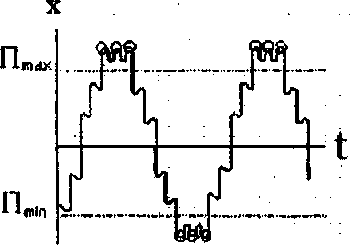
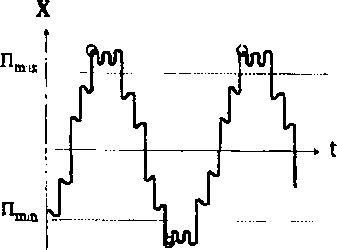
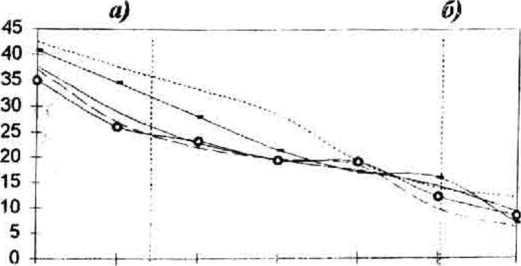
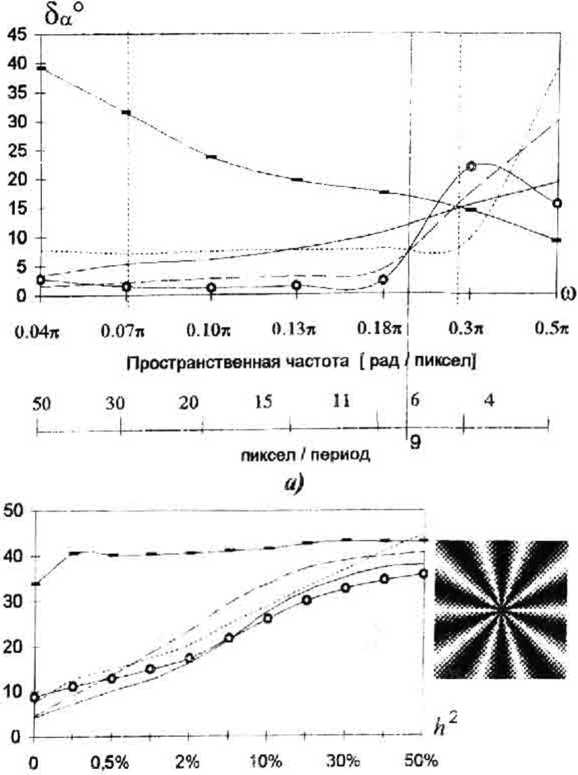
Полученная ошибка зависит от уровня шума, от пространственной частоты (рад/пиксел) (или от периода анализируемой структуры d = 2л/со (пик-сел/период)) и от метода построения поля направлений. Дтя полноты экспериментальных исследова- ний данного класса методов проведем также тести- к5 = ^ л Ь-2«‘’у)-е‘2^:
\2
= Лт Jf sin2 (* у) - ф(х, у, И^О
(Н)
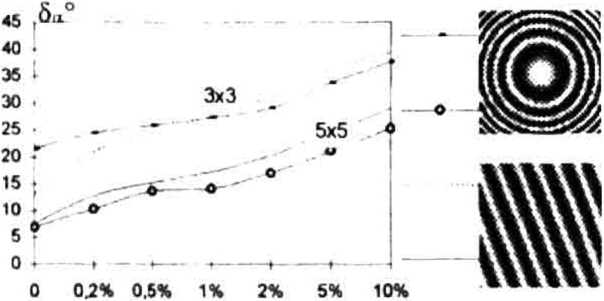
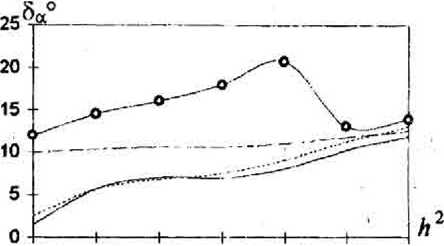
Значение среднеквадратичной погрешности находится в диапазоне от нуля до четырех. При этом нулевое значение соответствует совпадению полей направлений, а максимальное - расхождению на 90°. В качестве значения погрешности будем использовать угловую среднеквадратическую погрешность: 5^ = arcsines2 /4 . Исследование точности проводилось на серии тестовых изображений, отличающиеся наличием шума, равномерностью и неравномерностью пространственной частоты и видом квазипериодической структуры (рис. 8). Рассматривалась зависимость точности оценивания от отношения шум/сигнал Ь^=<з2/с2, где af -дисперсия функции яркости:
а/ = т^Л(7(х..у)-7)2^-
Ио полос; д) с шумам 50%.
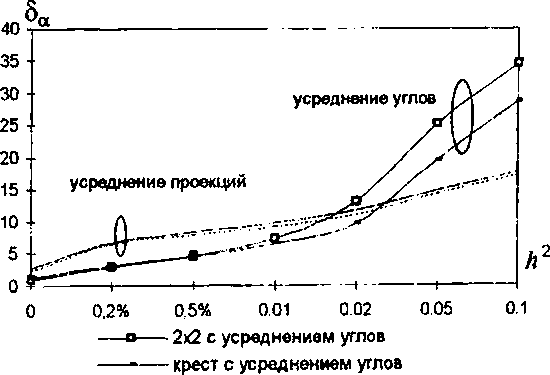
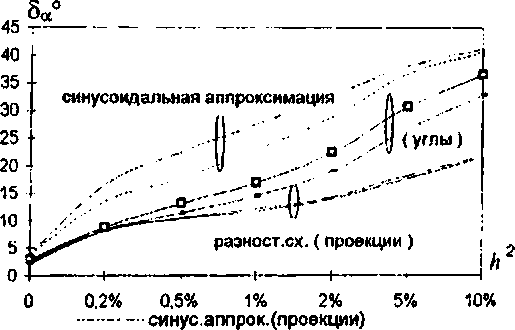
рование переборного метода цилиндрической полиномиальной аппроксимации [8]. Сравнивая между собой методы параболической аппроксимации и аппроксимации плоскостью (рис.9, 10). можно сделать вывод, что метод аппроксимации плоскостью.
обладая наименьшей вычислительной сложностью, обеспечивает наилучшую оценку поля направления.
О 0,2% 0,5% 1% 2% 5% 10%
................ПЛОСКОСТЬ
—о — параболоид --комбинированный -------переборный цилиндрический
Рис. 9. Зависимость точности оценивания поля направлений аппроксимационными методами от интенсивности шума (маска 11x11, со=0.07т^.
Это объясняется тем, что на тестовом изображении площадь участков, соответствующих перепаду функции яркости (рис.6) больше, чем участков, соответствующих точкам экстремума. Можно заметить также существенное уменьшение погрешности оценки поля направлений при использовании комбинированной аппроксимации.
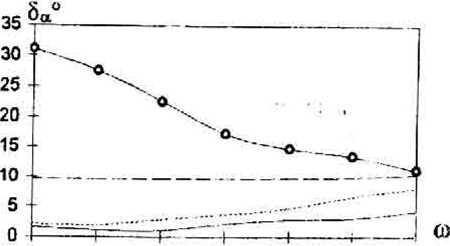
0.02л 0.03л 0.04л 0.07л 0.1л 0.13л 0.17л Пространственная частота ю [ рад / пиксел)
.......-.......плоскость ,
—о параболоид -------комбинированный
------переборный цилиндрический
Рис.10. Зависимость погрешности оценивания поля направления аппроксимационными методами от пространственной частоты квазипе-риодической структуры (маска 9x9).
-
3.2. Методы локальных градиентов
Рассматриваемый класс методов основан на том факте, что градиент функции в любой точке перпендикулярен касательной к линии уровня в этой точке. Методы локальных градиентов основаны на вычислении градиента функции яркости при различных положениях локальной маски внутри сканируемого по изображению симметричного прямоугольного внешнего окна
И7
размером
М
х
N
(локальный градиент): (//
3 Jy
z), где
1
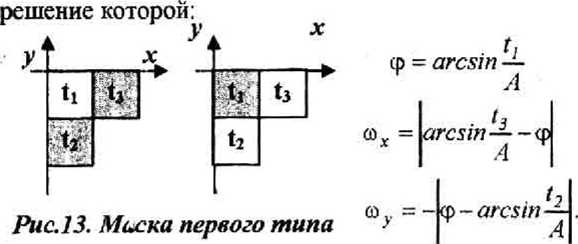
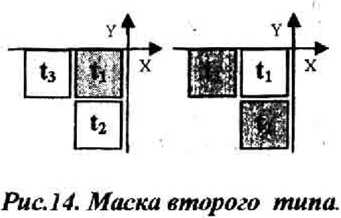
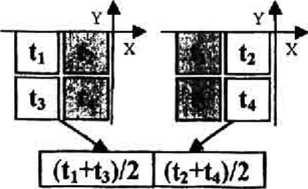
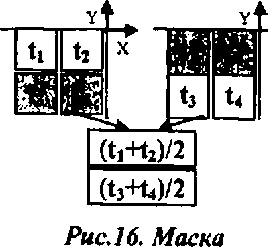
Использовались два типа локальной маски (рис. 11). За направление полос в точке сканирования принимаем угол ц/, вычисленный на основе найденных локальных градиентов:

Рис.11.
tg Ч^) = -Л / fу.0 5 wM < 7С , где
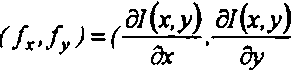
Рассматриваемый класс мето
дов нахождения поля направления можно разбить на два подкласса.
характеризуемые различным способом использова ния локальных градиентов в общей схеме расчета поля направлений: методы усреднения проекций градиента и методы усреднения локальных углов направления. Метод усреднения проекций градиентов основан на использовании локальных градиентов ^Jk3 Jy'^. соответствующих положению (к,Г) локальной маски , в расчете градиента функции яркости в центре внешнего окна W.
-
1 NM ы ы
к=1Ы
Метод усреднения локальных углов направлений использует локальные градиенты ^Д J,*1^ для расчета локальных углов:
Vk.i = -arctg(Jxu //уи).
Тогда направление полосы в центре внешнего окна W можно вычислить усредняя поле локальных углов:
W^^g^exp^vVkjY
- к=11=1
Значение весовой функции поля направлений соответственно будет иметь следующее выражение:
1 n м , ,
w = — 2 Zw^/J .
MN k-_iui
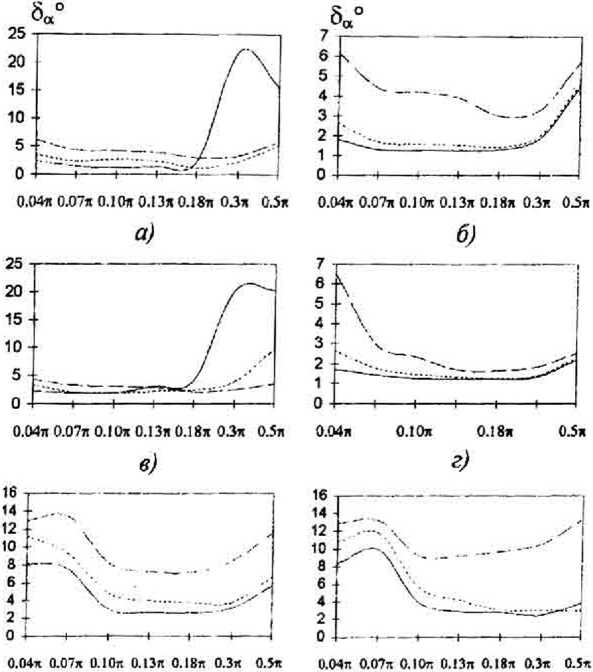
Фактически метод состоит из двух этапов: 1) определение градиента, либо направления (на основе градиента) в каждой точке локальной маски (2x2, крест); 2) сглаживание поля градиентов или поля направления в окне. Процесс классификации методов градиентов можно продолжить, базируясь на различных способах нахождения локальных градиентов: использование разностных схем и локальной аппроксимации гармоническими функциями. Общая классификационная схема для класса методов локальных градиентов представлена на рис. 12.
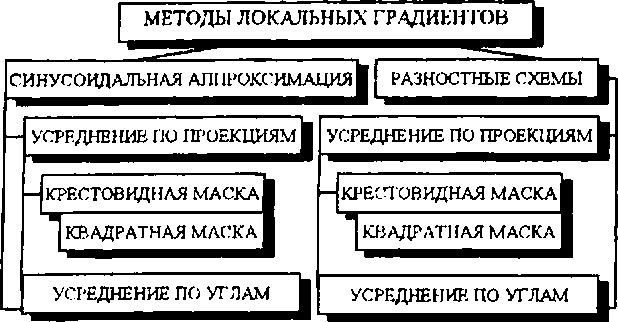
Рис. 12. Классификация методов локальных градиентов.
Градиентный метод с использованием разностных схем. В этом методе для нахождения градиента используется его определение. При вычислении частных производных применяется разностный метод со сканированием локальной маской двух видов: квадратная размером 2x2 и крестообразная. Эти методы, как и все градиентные, позволяют получить непрерывные значения угла направлении, что обеспечивает повышение точности оценивания по сравнению с переборными алгоритмами. Быстродействие методов существенно зависит от размера внешнего окна сканирования W. Недостатком метода является повышенная чувствительность к шумам.
Методы локальной синусоидальной аппроксимации. Методы описываемого подкласса градиентных методов основаны на аппроксимации в пределах локального окна функции яркости синусоидальной функцией двух переменных: р(х,у^ = = Asin^x + m^y + ^p). Значение локальных проекции градиента в центре окна (при х=у=0):
Jx =А tox
cos| jy =А toy СОЗ(ф ). Параметры A, мх , юу, ср, можно определить методом наименьших квадратов, который сводится к системе нелинейных уравнений, которую аналитически решить невозможно. Численные методы очень сложны в реализации, а в данном случае ненадежны в связи с неоднозначностью обратных тригонометрических функций. Поэтому данная задача решается без использования метода наименьших квадратов и формулируется таким образом, что допускает аналитическое решение. Величина А является константой, равной наибольшему значению функции яркости. Необходимо определить параметры юх, Юу, ф. Применим метод сведения переопределенной задачи к такой, где число уравнений равно числу неизвестных. Для этого перейдем от используемого нами вида локальной маски к маскам нескольких видов. Маска первого типа соответствует наклону7 полосы в центре окна на 45° и используется при определенной конфигурации значений яркости, соответствующей условию (рис. 13): [^ < ч Нч < ч )M(g > ч Hi > ч)] • (14) Выберем стандартную декартову систему координат, обеспечивающую наименьшее значение фазы (что определяется неоднозначностью арксинуса при выполнении условия (14)). Для данной задачи важен лишь знак частного юх / ©у. Поэтому частоту' ©х считаем всегда положительной, а юу с данной маской при выполнении условия (14) - отрицательной. Это всегда можно сделать выбором начала отсчета и начальной фазы. Таким образом, если условие (14) выполняется, то приходим к системе следующего вида: Asincp =t, - Asin (-to у -Kp)=t2 ' [Asin(tox+ Если условие (14) не выполняется, воспользуемся маской второго типа (рис. 14), соответствующей наклону полосы в центре окна на 135° (14). Частоты ©х ,©у являются положительными и система уравнений будет иметь вид: . з {As imp =1 ] Asin(-to V-Kp)=4 Asin (-to х + (p)=t3 решение которой: Ч Ф = aresm —, Т А ч = <ь-aresm— А Маска третьего типа соответствует наклону' полосы в центре окна на 90° (рис. 15), что соответствует выполнению следующего условия: Ik <чИч <^)№ > чНч > 'JL (15) В этом случае частоты: ©х>0, ©у =0, и система уравнений будет иметь следующий вид: Рис.15 Маска типа три. aresm—— 2А -Ф , toy = 0. ,. ч+ч Asmtp = ? ■ Asin(toх + ф> = ■■ ? -решение которой: . ч+ч Ф = aresm -----, 2А Маска четвертого типа соответствует горизонтальному расположению полос (рис. 16), что соответствует выполнению следующего условия: К'- «1И'2 «JMh XjbfoxJL «в) четвертого типа. . ч+ч Ф = aresm —■■, cov Аналогично частоты: ©х=0, toy>0, и система уравнений имеет вид: ' • Ч^Ч Asm Л5Ш<-ЮЛ, +ф) = ^—-^ решение которой: = ф-ОГСЛ/Л Во внешней маске W укладывается (M-l)x(N-l) локальных масок размером 2x2. Таким образом для определения частоты функции яркости, соответствующей центру глобального окна W используются усредненные по окну значения модулей локальных к.1 к.1 частот cor,а>у : 7 M-lN-h I ; ™^(м-/ха'-/)££М При этом частотным компонентам юх и соу присваивается тот знак, который преобладает во множестве локальных частот. На рисунках 17 - 19 приведено исследование точности оценивания поля направления градиентными методами в зависимости от интенсивности шума и пространственной частоты квазипериодической структуры. ------2x2 с усреднением проекций ..............крест с усреднением проекций Рис. 17. Зависимость погрешности оценивания поля направления от интенсивности шума (маска 7x7) для класса градиентных методов, использующих стандартные разностные схемы. синус.аппрок.(углы) разност.схемы, (крест- проекции) ---разност ,схемы.(крест- углы) ----разност.схемы.(2х2- проекции) —о— разност.схемы.(2х2- углы) Рис. 18. Зависимость погрешности оценивания поля направления от интенсивности шума (маска 7x7) для различных градиентных методов. Синусоидальный метод является устойчивым к шуму при увеличении пространственной частоты квазипериодической структуры. Методы, основанные на разностных схемах, использующие усреднение проекций обеспечивают более высокую помехоустойчивость при достаточно большой интенсивности шума, однако методы, использующие усреднение углов обладают тем преимуществом, что являются более точными при высоких пространственных частотах. д) е) 3. 3. Дифференциальные методы Рис. 19. Зависимость погрешности по- - -^ строения полей направлений от частоты 5x5 полос. Разностные схемы: а) крест-проек- 9x9 цаи, б) крест-углы, в) 2х2-проекции, г) 2х2-углы. Синусоидальные методы: д) усреднение углов, е) усреднение проекций. Дифференциальных методы основаны на том факте, что производная функции яркости по направлению, совпадающем)' с направлением полосы, имеет наименьшее по модулю значение среди производных по направлению в текущей точке: ф - arg тт\р(^)\. При использовании дифференциального метода с маской 3x3 по отсчетам внутри окна вычисляем производные вдоль направлений, определяемых углами 0. 45, 90. 135° (1J. При этом используются симметричные разностные схемы: J (х0) = нт--------—-------. и-^о 2п При использовании маски размеров 5x5 вычисляются производных по восьми направлениям, определяемых углами: 0, 26=arctg( 1/2), 45. 63=arctg2, 90. 116, 135. 153° 111. Основным преимуществом дифференциальных методов является максимально возможное быстродействие среди всех представленных классов методов построения поля направления. Весовую функцию определим соотношением: » =(таЦ/7ф)(-т<п1/7ф,^/ma^/Vq>^ Существенным недостатком дифференциальных методов является сильная чувствительность к шумам, что дает более низкое качество оценки по сравнению с другими методами. На рис 20 показана зависимость пырсшности оценки поля направлений для шперферырамм от интенсивности шума. Рис.20. Зависимость погрешности построения паля направлений дифференциальными методами от интенсивности шума Ди» двух типов квашпериодических структур. Основным ограничением методов является принципиальная невозможность уменьшения мак-симальной ошибки оценивания до значений меньших чем УО^п. где п - количество производных по направлению (л 4 хтя маски 3x3, nN- 5x5). 3 4 Проекционно-дисперсионные методы Проекционно-дисперсионный метод построения поля направлений основан на применении пре-обраюванни Радона |9| хтя вычисления “томографических' проекций функции яркости изображения hx.y# внутри скользящего окна вдаль направления перпендикулярного направлению, задаваемому углом ч' (рис 21) ’(\Г ♦ г' cos( ц/ + arctg —), ‘ (IK) I' * : мп(\у t arctg —))dz i де предполагается, что центр окна размера ТхТ находится в точке (0,0) Рассматривая функцию (18) при фиксированном значении параметра у и значениях аргумента 1е(-Т 2. Т 2). можно измерить разброс шаченнй относительно среднего (дисперсию) T 2 . 1 T 2 la оценку значения поля направлений прини Непосредственное использование преобразование Радона (18) для дискретного случая вызывает трудности, связанные с невозможностью вращения окна обработки Практическая реализация дисперсионного метода построения поля направлений сводится к вычислению функции D<\y) хтя частного случая четырех (вертикального, горизонтального и диагональных) направлений на дискретном множестве отсчетов функции яркости 1(х,у) внутри окна Произведем сканирование изображения 1(х.у) квадратной МхМ маской и хтя каждого из ее положений сформируем четыре последовательности средних значений хтя отсчетов, расположенных вдоль линий, параллельных одному из четырех направлений: 0, 45. 90, 135° R^,45^= - V](k -j* Li)Л = U.. JM - L k K^0^= — LJfi.k)3< = 1.2.....M; M (-/ R^.O'^l-v/fkj)^ = 1,2.,_M; (19) R^JjS^L^jfM-k+j-lj). k = 1,2,...2M - 1. В результате получаем дискретный вырнант °М^ !.vkkAv1lR( * (20) ^(ч/) = ^у(*.ч,№.ч/) мается значение угла ц*. доставляющее максимум функции i^v) ф = arg maxD^yY Весовую функ цию комплексного поля направления определим из следующего соотношения w = 1 znar D^vV mm ^Й max D^ ~. к = 1,2......V/, зр = 0 или ц/ = 90 ^)=U;.Ы k-_12....2M.L । М М ) I у =-/5*илм ц/=/35*. Основным недостатком такой реализации [ 11 проекционно-дисперсионного метода является кван-тованность результирующих значений поля направлений (0" 45". 90° 135") Можно увеличить число дзалаций до восьми, обобщив выше приведенные соотношения за счет рассмотрения четырех дополнительных направлений 26 уurctgll 2). 63u Рис.22. Иллюстрация дисперсионного .истода с интерполяцией. Дисперсионный метод с интерполяцией. Допустим, что функция /Д\|/) имеет вид синусоиды D^ = ?1 cos^v - ф))+ В Зная значения функции ^o«^45^9O^bs в точках \|/=0°, 45°.90°. 135°, можно оценить неизвестные значения параметров Аа,В . A cos 2\у + В = 1)0 .4 сом — - 2ф V В = О4< ^0 + ^45 "*" ^90 + ^135 ~ ^ откуда полу чаем tg2w=(D45-B)/fD0 -В) (21) На отрезке [0°, 180°| данное уравнение имеет два решения, соответствующих минимальному и максимальному значению функции IXxvY Д;,я да»' кого метода весовую функцию поля направления определим следующим образом и 2А (А В> Рис. 23. Зависимость погрешности построения полей направлений проекционно-дисперсионными методами от интенсивности шума для двух типов квазипериодических структур Исследование точности проекнионно-дисперсионных методов (рис. 23-25) показало, что интерполяционный метод в 2 - 12 раз увеличивает точность оценивания поля направления по сравнению с четы-рсхградационным переборным методом (рис 23) Интерполяционный метод проитрываст переборному только для больших значений пространственной частоты и большой интенсивности шума 40 . 5 0 3x3 с переТюрнмй —•--• » ^ ИИТОрПОЛЯЦИОННЫЙ 0.2% 0.5% 1% nepetxjp 3x3 о перебор 13x13 Интерпол 9x9 . , ,/т' 2% 5% 1С% перебор 9x9 Интерпол 3x3 Интерпол 13x13 Рис.24. Зависимость погрешности оценки полей направлений проекциокно-дисперсионными методами от интенсивности шуми для различных .масок. 15 ■ I4 5 , 14 . 13.5 • 13 , ■2 5 1 12 1 115 | '.Мх МГж ЦИт 1|Зя ОЛИж 03* 05* о) переборный Z, 20 • 15 • 10 . $ I .- - ” О...... 0/14* ЩГ* । Кт 014 ЫЯ» 03* 'i.S. б/ интерпачяционный Рис. 25. Зависимость погрешности оценки пазя направлений проекционными методами от пространственной часто ты квази периодической структуры 3 5 ( пектральные методы С центральный метод основан на модели изображения с локально-периодической функцией яр-Кости В соответствии с этой моделью производится Спектральный анализ функции яркости изображения ^xa) в пределах скользящего окна IVlx^vry ^Цх„л,^ |(.r. y) |x-r,Js 7/2л - ^Js/72). где х'<> у(1з - координаты центра окна 7 х 7-размеры окна ‘ij Рассмотрим коэффициенты ряда Фурье функции •I экости в пределах окна jj/(x.y )ехр ^у (тх + п у) | dxd\ 1 определим координаты максимального по модулю о эффицистпа km,,.n„ ) - org тах^( (т. п) I т.п I/O) 01 Индексы fm Рис.26. Иллюстрация спектрального метода. ______ (22) Цхо-Уо^-у-^"^’ В отличие от метода локальной квадратичной аппроксимации здесь размеры окна ограничены снизу: при каждом положении на плоскости изображения оно должно пересекаться несколькими “интерференционными” полосами. Чем больше полос попадает в окно и чем меньше искривленность полос внутри окна, тем более точными будут оценки (22). Практическая реализация спектрального метода расчета поля направлений основана использовании рекурсивных алгоритмов быстрого преобразования Фурье. Но, несмотря на это, данный метод чрезвычайно трудоемок с вычислительной точки зрения. Рассмотрим метод основной локальной частоты, основанный на непосредственном “геометрическом” способе оценивания пространственных частот. Метод основной локальной частоты. Этот метод также как и представленный выше спектральный метод, основан на поиске главной гармоники. Отличие заключается в процедуре поиска. Компоненты пространственной частоты для малой области изображения квази периодической структуры равны cox=2n/dx) а)>^2л/с!>, где dx. dy- периоды функции яркости 1(х, у) в вертикальной и горизонтальной развертке, задача сводится к определению периода сечений функции яркости по горизонтали Рис.27. Иллюстрация метода основной локальной На рис.27 отмечены по вертикали и горизонтали периоды функции яркости, равные удвоенному расстоянию между' соседними экстремумами (минимумами и максимумами). В силу наличия шумов на рассматриваемых сечениях функ- частоты. ции яркости присутствуют побочные минимумы и максимумы. Поэтому необходима процедура их отсечения. Отбросим минимумы, лежащие выше порогового значения Пшт и максимумы - ниже порогового значения Птах (на рис.28 они соответственно обозначены - 0 и *). В результате на ярких участках группируются максимумы, не разделенные минимумами, на темных -минимумы. X Рис.28. Удаление ложных экстремумов. Поскольку экстремумы разных типов должны чередоваться, то воспользуемся процедурой прореживания. При этом оставим один первый максимум (минимум), остальные до ближайшего минимума (максимума) отсечем (рис.30). Для определения пространственной частоты просканируем исходное изображение. Размер маски должен составлять приблизительно два - три периода функции яркости. При увеличении размера маски нарушается условие однородности квазиперио-дической структуры, при уменьшении - возрастает влияние краевых эффектов. Рис.29. Удаление группы экстремумов. Для каждой текущей точки, соответствующей центру окна, определим значения пространственных частот сох и щ. В соответствии с размером маски сформируем периодически обновляемый буфер из строк (столбцов) изображения. Выберем в маске первую, среднюю и последнюю строки (столбцы). В каждой строке (столбце) определим количество и номера минимумов и максимумов (отсчетов с наименьшими и наибольшими значениями яркости). Рис.30. Удаление соседних экстремумов. Определим среднее расстояние между пиками (максимумами) в строке (причем расстояние равно нулю, если пиков в строке (столбце) нет, и размеру' маски, если пик один), и определим соответствующее значение частоты. Результирующую частоту определим как среднее значение найденных частот по выбранным строкам (столбцам) сканируемой маски. Оценка значения поля направления равна отношению найденных компоненту и у. В отличие от спектрального или градиентных методов в данном случае возникает неоднозначность, связанная с невозможностью определения знаков компонент пространственной частоты. В данном случае мы не сможем отличить направления о. и (180 - а). Для определения знака частоты предлагается анализировать сдвиг экстремумов функции яркости в соседних линиях развертки изображениях. На рис.31 в приведено исследование точности оценивания поля направления в зависимости от пространственной частоты квазипериодической структуры для различных размеров окна сканирования. На рис.31а.б приведена точность оценивания поля направления при различной интенсивности шума для двух сечений данного графика, соответствующих низкой и высокой частоте структуры. При увеличении пространственной частоты повышается точность оценивания поля направления. При наличии шумов погрешность достаточно высока, но не сильно увеличивается при увеличении интенсивности шума (это объясняется природой накладываемого шума (высокочастотной) и тем, что спектральные методы хорошо работают на высокочастотных ква-зипсриодических структурах (размер окна обработки ограничен снизу и должен содержать как минимум несколько “интерференционных” полос). О 0.2% 0,5% 0,01 0,02 0,05 0,1 0 0,2% 0,5% 1% 2% 5% 10% 0.04л: 0.07я 0.10л 0.13л 0.18л 0.3л 0.5л Пространственная частота ^ [ рад / пиксел] 50 ,30 .20 .15 , 11 ]6 . I— р р----1------1--1' пиксел / период d маска 5x5-- маска7x7 --------маска 9x9 маска11x11 —-о---маска13x13 Рис.31. Зависимость погрешности построения полей направлений методом “основной локальной частоты” а),б) от интенсивности шума для различных масок и различных частот: а) оз=О.Зл. б) <о^0.08л ; в) от пространственной частоты. 4. Экспериментальные исследования методов построения поля направлений На рис. 32 приведено исследование точности оценивания поля направления различными методами в зависимости от пространственной частоты, а гак же от периода анализируемой квазипериодической структуры при обработке окном 9x9 (дифференциальные методы окном 5x5) и в зависимости от интенсивности шума для высокочастотной интерферограммы рис.32в и низкочастотной рис.326, соответствующих сечениям графика рисунка 32а. 0 0,5% 2% 10% 30% 50% дифференциальные ------проекционные —о—градиентные (2x2) — -аппроксимационные ---спектральные Рис.32. Зависимость погрешности оценивания поля направления разными методами (маски 9x9): а) от пространственной частоты; б), в) от интенсивности шуми: б) при <0=^0.07л рад/пиксел, изображение 256x256, в) при а>=0.3л; размер изображения 128x128 пикселей. Максимальную теоретическую точность (при отсутствии шумов) обеспечивают градиентные и аппроксимационные методы построения полей на- правлений. При уровне шума 0.2?/о и выше преимуществом по точности оценивания поля направления (в диапазоне низких частот) обладают проекционно-дисперсионные методы. Для высокочастотных ква-зипериодических структур преимущество данных методов начинает проявляться при уровне шума 0.5% и выше, при этом в случае наличия большого шума методы являются достаточно помехоустойчивыми. и ошибка оценивания практически нс зависит от уровня шума. Для высокочастотных квазипе-риодических структур наилучшую точность оценивания поля направления обеспечивают спектральные методы. Влияние шума начинает сказываться на работе спектральных методов в диапазоне высоких частот при отношении шум/сигнал 5%. Для дифференциальных методов наблюдается резкое возрастание ошибки оценивания при пространственных частотах квазипериодичсской структуры выше 0.3л рад/пиксель, для данных методов можно также отметить сильную зависимость от шумов. Аппроксимационные методы обеспечивают хорошую точность оценивания поля направления, если окно обработки захватывает нс более одной полосы квазипериодичсской структуры. Наибольшим быстродействием обладают аппроксимационные, дифференциальные методы, метод основной локальной частоты. 40 35 30 25 20 15 10 5 О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 I-дисперсионный переборный. 2-дисперсион. интернач.; 3-дифференциалъный; 4-градиентный (синусоидальп. Ап-прокс.) с усреднением углов; 5-градиентный (синусоидальн. аппрокс.) с усреднением проекций. б-градиентный (разностные схемы) с усреднением проекций (2x2); 7-градиентный (разностные схемы с усреднением углов (2x2); 8-градиентный (разностные схемы с усреднением проекций (крест); 9-градиентный (разностные схемы) с усреднением углов (крест); 10 - цилиндрическая аппроксимация; J1-аппроксимация плоскостью; 12-аппроксимация квадратичной поверхностью; 13-комбинированная аппроксимация; 14-спектральный (основной локальной частоты). Рис.33. Диаграмма затрат времени на обработку квазипериодической структуры размером 256x256 различными .методами построения полей направлений d /я различных масок. 5. Примеры практических задач, решаемых с использованием поля направлений 5.1. Анализ дактилограмм. Дактилоскопические изображения широко используются в криминалистике для идентификации личности правонарушителя, а также в некоторых типах устройств для ограничения доступа персонала. Представленная в работах [1, 10] методика кодирования изображений отпечатков пальцев основана на обнаружении глобальных и локальных особенностей и расчете их геометрических характеристик (расстояния и утлы между особыми точками). К глобальных особенностям относятся тип узора (“петля”, “дельта1', “спираль” и т.п.). Локальные особенности - это точки разрыва, ветвления и слияния линий папиллярного узора. Метод поля направлений может быть применен для обнаружения и определения координат глобальных особенностей, для оценки их геометрических характеристик и для построения процедур поиска локальных признаков дактилограмм. Для вычисления поля направлений в данном случае возможно использование спектрального или дисперсионного методов (метод локальной квадратичной аппроксимации не применен из-за высокой густоты полос, сравнимой с частотой дискретизации дактилографического изображения). В данных исследованиях был использован проекционно-дисперсионный метод, дающий четыре градации направления, а также градиентный метод с использованием синусоидальной аппроксимации. На рис. 34 приведены исходное изображение и результаты расчета и фильтрации поля направлений. а) б) в) Рис.34. Поле направлений дактилокарты а) функция яркости исходного изображения; б) четырехградационное поле направлений; в) результаты линейного сглаживания. Распознавание типа папиллярного узора осно- Шатер Спираль Рис.35. Глобальные особенности вано на анализе конфигураций поля направлений на границе скользящего окна. При этом используется четырехградационное поле направления. Для приведения непрерывных значений к четырем градациям воспользуемся номерами секторов (0, 1, 2, 3), определяемые следующим диапазоном углов: [0°-22°, 158°-180°1; [23°-67°]; [68°-1120]; ”[ПЗ°-157°]. Центры приведенных диапазонов соответ ствуют углам 0°, 45°, 90°, 135°. Окрестность каждой точки дактило- граммы характеризуется Конфигурация Тил точки 1-0-3-2-1-0-3-2 0-3-2-1-0-3-2-1 3-2-1-0-3-2-1-0 2-1-0-3-2-1-0-3 Центр спирали 0-1-2-3/1-2-3-0 2-3-0-1/3-0-1-2 Дельта 1-0-3-2/-3-2-1 3-2-1-0/-1-0-3 Петля 2-1-0-1 дв.левая петля 3-2-3-0 дв.прав.петля 1-0-3-0 Шатер Рис.36 определенным порядком смены значении поля направлений. Для глобальных особенностей этот порядок отличается от порядка произвольной точки отпечатка (рис.35,36). Оценивание геометрических параметров глобальных особенностей Применение поля направлений позволяет существенно упростить алгоритм распознавания и анализа глобальных и локальных особенностей. 5.2. Анализ кристаллограмм В настоящее время в офтальмологии существуют методы диагностики глазных болезней по состоянию кристаллограммы слезной жидкости пациента. Основными признаками патологичности являются большое количество центров кристаллизации, большой разброс направлений и высокая плотность кристаллов [2, 3] (рис. 39). производится на основе геометрии секторов поля направлений, В качестве геометрических параметров глобальных особенностей используются; угловые характеристики дельт, наклон оси спирали, характеристики закручивания спирали: степень отклонения от вертикали, размах секторов поля направлений слева и справа от центра, признак несимметричности расположения дельт (рис.37). Рис.З7. Геометрические характеристики л зоба. зьных особен к остей. Для поиска локальных особенностей (точек разрыва, ветвления и слияния папиллярных линий) используются традиционные методы получения бинарных препаратов изображений и дальнейшая их логическая обработка с использованием поля направлений (рис.38). Классификации подвергались точки, которые лежат на качественных областях, определяемых критериями качества, полученных на основе анализа изображения скелетизированного папиллярного рисунка и весовой функции поля направления. __________________„ Рис.38. Лшсш >' проклассифицированных локальных особенностей папиллярного рис) нка. Кристи сыгра-М-Чы нити, испей Рис.39. Характерные и «обряжения кристалла, пи м.н слезной жидкости г. норме и про натеюгических измен- пнях органах зрения. Данными признаками также обладают кристаллограммы плазмы крови [11], используемые аналогично для диагностики ряда заболеваний. На рис.40 приведены образцы кристаллограмм плазмы крови и соответствующие поля направлений с основными характеристиками. Для анализа степени разброса направлений крисгаллизации используется графический препарат поля направлений, на основе которого определяется коэффициент однонаправленности: В качестве признаков классификации были выбраны также следующие характеристики кристаллограмм, построенные с использованием поля направлений: относительная площадь областей с выраженным направлением KM = SV /S . где \,- пло щадь участков, выделенных на основе анализа весовой функции поля направлений, 5 - площадь кристаллограммы; густота лучей, определяемая на областях четких линий Dv: ^, =г—г]|'(«,+ovyVnA". ' Ио, прозрачность кристалла. Knp=(lv-1^,) Iv, где А■ = |77Т Яу(х.y) пато. югия Исходное Сглаженное Весовая функция Контурный препарат изображение ноле направлений ноля направлений поля направлений Рис.40. Анализ кристаллов плазмы крови 5. Заключение Эффективным методом анализа изображений, характеризуемых наличием квазипериодических структур, является метод поля направлений. Он позволяет сократить структурную избыточность таких изображений, упрощает обработку и анализ, повышает качество распознавания. Метод поля направлений дает возможность выявить существенные признаки изображений, позволяющие провести эффективный анализ. В представленной работе предложены численные методы оценивания поля направления и сравнительное исследование их точности и быстродействия. Все методы разбиты на пять классов в зависимости от используемой модели представления поля направлений и подхода к его вычислению: методы параметрической аппроксимации. методы локальных градиентов, дифференциальные методы, проекционно-дисперсионные методы, спектральные методы. Для оценивания точности методов в качестве критерия использовалась приведенная угловая среднеквадратичная погрешность, рассчитанная с использованием комплексного представления поля направлений. Разработанная классификационная схема методов построения поля направлений позволяет осуществить выбор наилучших методов для конкретных задач обработки изображений