Численные методы обучения искусственной нейронной сети
Автор: Андреева Елена Аркадьевна, Мазурова Ирина Сергеевна
Журнал: Ученые записки Петрозаводского государственного университета @uchzap-petrsu
Рубрика: Физико-математические науки
Статья в выпуске: 8 (145) т.1, 2014 года.
Бесплатный доступ
Решается задача моделирования и обучения искусственной нейронной сети достаточно общей топологии, динамика которой описывается системой интегро-дифференциальных уравнений. Задача обучения искусственной нейронной сети рассматривается как задача оптимального управления с нефиксированным временем. Сформулированы необходимые условия оптимальности весовых коэффициентов искусственной нейронной сети и внешнего управляющего воздействия с учетом заданных ограничений и вида функционала. Исходная задача сведена к дискретной задаче оптимального управления, которая решается на основе методологии быстрого автоматического дифференцирования. Проведен анализ влияния параметров задачи на оптимальное решение.
Искусственные нейронные сети, интегро-дифференциальные уравнения, оптимальное управление
Короткий адрес: https://sciup.org/14750775
IDR: 14750775 | УДК: 519.7
Текст научной статьи Численные методы обучения искусственной нейронной сети
В последние десятилетия большое внимание уделяется исследованию искусственных нейронных сетей, которые эффективно используются в различных системах управления, медицине и экономике. В статье рассмотрена проблема моделирования и обучения искусственных нейронных сетей с достаточно общей топологией, описываемой системой интегро-дифференциальных уравнений. При этом целью обучения является минимизация ошибки обучения, энергии сети и времени обучения, то есть решается много -критериальная задача. Для решения этой задачи используется аппарат математической теории оптимального управления, с помощью которого находятся оптимальные значения весовых коэффициентов дискретной нейронной сети. Заметим, что таким способом может быть решен большой класс задач, включающих создание ассоциативной памяти, модель распознавания образов, прогнозирования и т. д.
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим математическую модель нейронной сети, в которой динамика отдельного нейрона описывается на основе биологических предпосылок [1], [5]. Искусственная нейронная сеть состоит из нейронов, каждый из которых взаимодействует со всеми остальными нейронами. Воздействие j -го нейрона на i -й нейрон в момент времени t характеризуется весовым коэффициентом w y( t ). Пусть x,(t ) - функция, характеризу-
ющая состояние i -го нейрона в момент времени t , i = 1, n . Динамика искусственной нейронной сети описывается системой интегро-дифференциальных уравнений:
x , ( t ) = - A x ( t ) + fr
^
УХ лА z ) x j ( z ) dz
V 0 j =1 / t е [0, T ]
+ Y i u , ( t ) ,
с начальными условиями x i (0) = 6 , , i = 1, n , (2) где e i — параметр, определяющий скорость затухания i -го нейрона при отсутствии внешнего воздействия, fi - функция активации, при этом Y i u , ( t ) - внешнее воздействие на нейрон в момент времени t . Коэффициенты е , , в, Y , , i, j = 1, n , — заданные неотрицательные параметры модели.
Весовые коэффициенты нейронной сети гоц ( t ) и внешние воздействия u , ( t ) являются функциями управления и ограничены __
|m ( t )| < a j , u i ( t )|^ a , , i , j = 1, n , п. в. t е [0, T ] (3) где a j , a i , i , j = 1, n , заданные положительные параметры модели, полагаем m ii ( t ) ^ 0.
Задача оптимального управления заключается в минимизации функционала:
Tnn
J ( m u ) J X £ “ j m ij 2 ( t ) + mr ( t»dt +
0 i = i j = i (4)
n
+ X MAx.(T) - A,)2 + T, где первое слагаемое характеризует энергию рассматриваемой нейронной сети, зависящую от текущей конфигурации сети, aj - параметр, определяющий меру влияния значения весового коэффициента между нейронами i и j и на минимизируемый функционал, второе слагаемое характеризует ошибку обучения нейронной сети, Mi - параметр, определяющий меру воздействия этого слагаемого на минимизируемый функционал, A - целевой вектор.
Задача оптимального управления заключается в том, чтобы обучить нейронную сеть таким образом, чтобы минимизировать функционал (4) и построить оптимальные значения весо-вых коэффициентов, внешнего управляющего воздействия. Задача оптимального управления с нефиксированным временем процесса была рассмотрена в работе [2] для модели искусственной нейронной сети, описываемой системой дифференциальных уравнений с запаздывающим аргументом.
НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
Особенностью поставленной задачи является большая размерность управляющих функций, наличие распределенного запаздывания и нефиксированное время процесса.
Для решения задачи (1)-(4) перейдем от задачи оптимального управления с нефиксированным временем процесса к задаче с фиксированным временем процесса. Для этого осуществим следующую параметризацию:
t( т ) = ^т , т е [0, T 0 ], t ( T ,) = # 0 = T и введем обозначения:
x ( t( т )) = Х ( т ), a ( t( т )) = а ( т ), u ( t( т )) = й( т ) .
В этих обозначениях задача оптимального управления примет вид:
T 0 n П
+ ай (т )2) dт + X M,(х( '" A)2 +1 (To), i=1
Построим функцию Понтрягина:
H ( t , x , y , а , й , £ r , p , 5 , ^ 0 ) = nn
= Л Х ( X a ij ( а j ( т ))2 + a U ( т )2) + i = 1 j = 1
n
+ X p ( т X— X x i ( т ) + ^ f i ( y ( т ) ) + ^Y i u i( т )) + (9) i = 1
n ( n А
+ X г ( т ) ^ x “ j( т ) хд т ) l+ 5 ( т ) ^ .
i = i i j = i j
Теорема. Пусть b)j (т), i, j = 1, n - оптимальные весовые коэффициенты, йi (т), i = 1, n - оптимальные управляющие внешние воздействия, ^ - оптимальное значение параметра, aij и ai отличны от нуля, тогда aij, Ф у<т) > aij
a ij ^т ) = 1Ф ij ( т )’! Ф ij ( т )l - a ij , i , j = 1, n , (10)
- a ij , Ф ij ( т ) <- a ij
т n
Х( т ) = - ^А Л -( т ) + ^ f - ^Ха z ) x j ( z ) dz + ^ А( т X
i = 1, n , t ( т ) = £ .
Введем новые переменные: т n ____ yi(т)=xJ X аj■(z) xj(z) dzi=1n ’
0 j = 1
такие что n yi(т) = ^X^bi,■ (т)Х,(т), i = 1,n, y(0) = 0.
j = 1
В этих переменных исходная система примет вид (6)-(8):
xv( т ) = ^P x i ( т ) + ^ f ( y i ( т ) ) + ^Y i u i i ( т X i = 1, n ,(6)
n y.(т) = ^X bj (т)Xj (тX i = 1 n’ j=1
t( т ) = § .
где
где
. , , Г(т ) x^ j (т ) . . ;— Ф ч ( т ) = , 1, j = 1, n ,
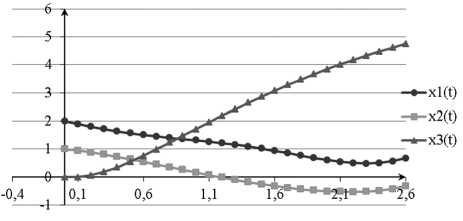
2Л^«а ai, т-(т ) > ai _ й.(т) = ki(т),|Т(т)| dH "^ n —. ■ a., T. (т) < — a. у (т) = Р-(т)Zi, i = 1, n , i 2Ла - Л) X (X an (‘bj■(т ))2+aui(т )2)+ +X р.(т)(—Pixi(т)+fi (yi(т))+^-z^i(т))+ i=1 +X г(т) X^bjХт)xc.j(т) + 5(т)=0, n n а система дифференциальных уравнений для сопряженных функций имеет вид (13): n pi(т) = §Р.(т X- ^X ги(т )(bji(т X i = 1,n (13) j=1 Г (т) = — ^Pi (т) ^f^y^, 5 (т) = 0, dyi с условием трансверсальности на правом конце (14): Pi(T) = —2Л Mi(X( T0) — A), i = 1, n — , (14) ГХТ0) = 0, i = 1,n, 5(T0) = — Л( ) ДИСКРЕТНАЯ ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ Для определения оптимального решения рассмотрим дискретную аппроксимацию начальной задачи, в которой используется правило левых прямоугольников для аппроксимации интеграла и схема Эйлера аппроксимации производных. Вводя следующие обозначения Ат = T0/ q, т* = * Ат, tq = To , x* = x^, y * = yт), bj^ = &j (Tk), й * = й4(Tk), i, j = 1,n, к = 0,q -1, построим дискретную задачу оптимального управления, которая состоит в минимизации функции: q-1 n n I (t, x, y b, й,Л) = АтЛ£ £ (£ « (b)4* )2 + к=1 i=1 j =1 n2 + ей*2) + £m,(x* -a,) + tq, i =1 при ограничениях xX*11 = x*-АЛДУ + А«. f, (y* ) + Ат(гй*, (16) n * 11 * * * У i = y 1 АтЬ ^bj xj , j=1 t*11 = t* + АтЛ, i = 1, n, * = 0, q -1. На функции управления наложены ограничения Ij^a,b,"=° И^a,, (17) i, j = 1, n, * = 0, q -1. Для решения задачи (15)-(17) в работе используется методология быстрого автоматического дифференцирования, разработанная в ВЦ РАН под руководством Ю. Г. Евтушенко, позволяющая с единых позиций определять градиенты для явно и неявно определенных функций и для вычислительных процессов, которые являются результатом дискретизации непрерывных систем, описываемых дифференциальными и интегро-дифференциальными уравнениями [4]. В соответствии с методологией быстрого автоматического дифференцирования введем множители Лагранжа p, r и s, тогда функция Лагранжа для данной задачи может быть представлена следующим выражением q-1 n n L(t, x, yb, йЛ,r, p, s, 4 = 4Ат^^ £ (£ « (b*)21 *=0 i=1 j=1 n 2 q-1 n 1^*2) 1 Atq 1 A£m,(xq -a,) 1££p*+1(x*11-x* 1 =1 *=0 i=1 1АтЛДX,k -АтЛ/(y*)-Ат/Д*) + q-1 £г,*+1(y*11- *=0 i=1 -yi* -АтЛ£Ь b)j5cj) 1q£s*+1(t*11-1* -АтЛ). j=1 *=0 Градиент минимизируемой функции 4L- = 24,АтЛейД - АтЛ/ip/-11, (1«) О ul dL 0bj = 2A0АтЛaljb),’m - АтЛгГ11xm, q-1n n 0L = A. Ат ££ (£«, (cbJ* )2+е,й*2) 1 °Л *=0 i=1 j=1 q-1 n +££ p? 11i.АтДx*-Ат/ (y*)-Ату,й*) + <20) *=0 i=1 q-1 n n q-1 1££ r*11(Ат £^fokxk)-£ s11Ат *=0 i=1 j=1 *=0 l, j = 1, n, *, m = 0, q -1, где n pim = pm11 - АтЛpГ11 Pl 1 АтЛ£ rm11 fo,™, (21) j=1 piq =-2A,Mi (xq - Al), (22) m = АтЛй"'11 fpm)- + rl"11, 0yl rtq = 0, sm = sm11, sq =-A,. (24) На основе быстрого автоматического дифференцирования разработан комплекс программ построения оптимального управления и проведен численный эксперимент, результаты которого представлены ниже. Заметим, что основное вычислительное время при расчете градиента по формулам (18)-(20) требуется на нахождение векторов p и r, для этого необходимо решить 2 системы уравнений с q • (n21 n) неизвестными. Проведено исследование зависимости результатов работы метода от параметров задачи. На рис. 1-2 представлены функции, соответствующие оптимальному состоянию нейронной сети, xР.t), г' = 1,3, и оптимальные весовые коэффициенты, (Ьу(t), i, j = 1,3. Целью работы нейронной сети является перевод ее из состояния x0 = (2,1,0) в состояние A = (1,0,5). Рис. 2. Весовые коэффициенты нейронной сети x,( t )J' = 1,3 Рис. 1. Функции состояния нейронной сети x, (t), г' = 1,3 Параметры режима, представленного на рис. 1-2, следующие: n = 3, T0= 5, Ат = 0,1, | uk |< 0,1, в, = 0,5, | to |< 1, a, = 0,1, Mi = 10000, точность метода ε = 0,000001. За 101841 итерацию значение минимизируемого функционала достигло величины 0,5176, что означает достаточно высокую эффективность метода, при этом оптимальное время процесса T = 2,8. В таблице приведены значения минимизируемого функционала при различном значении времени процесса T = 2,8 значение величины ошибки обучения и энергии нейронной сети достигает наименьших значений, при уменьшении или увеличении времени процесса увеличивается значение минимизируемого функционала. ЗАКЛЮЧЕНИЕ Аналогичный подход распространяется на оптимальное управление моделью искусственной нейронной сети, динамика которой описывается следующей системой интегро-дифференциаль- ных уравнений: n Значения минимизируемого функционала при различном значении времени процесса T 2 2,2 2,4 2,6 2,8 3 3,2 Iopt 2002,4 7,203 0,559 0,558 0,518 0,686 0,723 Iopt1 0,9402 1,034 0,559 0,558 0,518 0,686 0,723 Iopt2 2001,5 6,169 9,9∙10–5 2,1∙10–5 7,3∙10–6 2,8∙10–6 2,4∙10–6 n x(t)=-Ax(t)+fi V^to(t)xj(t-5j)dT + y-u-(t), ^t-r j=1 t e[0, T ] q-1 n n __ где Iop1 ЛгЕЕ (X«y (tok )2+^n,2), k=1 i=1 j=1 n2 *opt 2 = 2 Mi( Xq - Ai) , IP = lopto tot 2. =1 Из таблицы следует, что найденное оптимальное время процесса T = 2,8 соответствует наименьшему значению минимизируемого функционала, то есть за время работы нейронной сети с начальными условиями x,(t) = 6*.(t), t e [-r -max(£,),0], i = 1,n , где параметр 8j, j = 1,n учитывает запаздывание при передаче сигнала от одного нейрона к другому, а параметр r в интегральном слагаемом в аргументе функции активации учитывает тот факт, что внешнее воздействие на нейроны ИНС накапливается на интервале запаздывания [t-r, t]. Решение задачи оптимального управления с фиксированным временем процесса для такой нейронной сети рассмотрено в работе [3]. * Работа выполнена в соответствии с Программой поддержки ведущих научных школ (НШ-5264.2012.1). NUMERICAL METHODS OF ARTIFICIAL NEURAL NETWORK TRAINING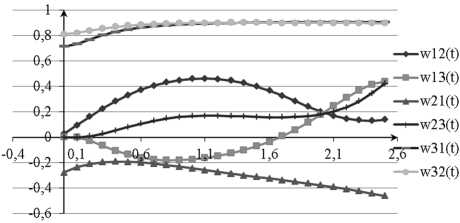
Список литературы Численные методы обучения искусственной нейронной сети
- Андреева Е. А. Оптимизация нейронных сетей: Учеб. пособие. Тверь, 2007.
- Андреева Е. А., Пустырнакова Ю. А. Численные методы обучения искусственных нейронных сетей с запаздыванием//ЖВМ и МФ. 2002. Т. 42. C. 1383-1391.
- Большакова И. С., Шаронов Д. А. Обучение нейронной сети с запаздыванием//Программные продукты и системы. 2011. № 2. С. 35-37.
- Евтушенко Ю. Г. Оптимизация и быстрое автоматическое дифференцирование. М., 2013. 144 с.
- Майоров В. В., Мышкин И. Ю. Математическое моделирование нейронов сети на основе уравнений с запаздыванием//Математическое моделирование. 1990. Т. 2. № 11. С. 64-76.


