Численные подходы к моделированию процесса экспандирования

Процессы экструдирования и экспандиро-вания основаны на гидротермической обработке корма под давлением. Принцип действия экструдеров и экспандеров одинаков – в шнековом рабочем органе продукт разогревается, уплотняется и выпрессовывается. Однако режимы обработки существенно различаются. В экструдерах продукт разогревается только за счет трения при движении по виткам шнека и активном перемешивании под давлением. Регулирование температурного режима обработки достигается в экструдере только за счет сменных рабочих органов. Обработка комбикорма в экспандере осуществляется при более высокой влажности. Продукт разогревается за счет ввода пара и трения. При одних и тех же температурных режимах обработка в экспандере при повышенной влажности протекает в менее жестких условиях. в экструдере из-за пониженной влажности на отдельных участках местные сопротивления движению продукта могут возрасти до значительных величин, вызывая местное повышение температуры, хотя общий температурный режим остается прежним. Как в экструдерах, так и экспандерах можно за счет изменения режимов обработки получать готовый продукт различной плотности. Вместе с тем, экспандирование имеет такие преимущества, как ввод большого количества жидких компонентов – масла, жира, мелассы, устранение вредных для питания компонентов, улучшение качества и усвояемости комбикормов, более высокую производительность пресса для гранулирования, лучшее качество гранул, использование более дешевого и сложного для гранулирования сырья. Эта задача решается с применением процесса экспандирования, который известен также под названием кондиционирование под давлением.

На выходе из экспандера продукт мгновенно теряет нагрузку, а добавленная жидкость в значительной степени испаряется. Называется это молниеносным испарением, поэтому последующей сушки готового продукта в основном не требуется. За счет испарения жидкости температура падает до 90 °С. В зависимости от рецептуры, температуры продукта и давления готовый продукт может иметь структуру теста, толстых хлопьев или комков. Гранулированный экспандат сочетает в себе одновременно преимущества гранулированных и рассыпных комбикормов. Каждая частичка содержит все составные компоненты. Распределение частиц очень равномерное. Можно регулировать размер частиц зазором в валковом измельчителе и получать рассыпной комбикорм, но без таких недостатков, как плохая текучесть и расслоение смеси. Обработка в экспандере уменьшает общую обсемененность сырья. Полностью уничтожаются колиобразные бактерии, кишечная палочка, плесневые грибки и сальмонеллы [1].

Постановка задачи.

Разница процессов экструдирования и экспандирования связана, в частности, с различием механических нагрузок, прилагаемых к единичному зерну. В процессе экструзии зерно разрушается под действием всестороннего сжатия, поскольку прохождение готового продукта через матрицу обеспечивает осевые нагрузки на материал внутри шнека. Экспанди-рование же осуществляемое через кольцевой зазор протекает под действием на зерно только радиальных сжимающих усилий. Соответствующая прочностная задача может быть описана следующим образом [2].

Будем считать оболочку тонкостенной, поскольку отношение наименьшего радиуса кривизны ρ min к толщине δ стенки оболочки (ρ min /δ) > 20 (рисунок 1) . В этом случае погрешность расчета по приведенным ниже формулам не превысит 5%.

Осесимметричная оболочка нагружена наружным давлением. В этом случае напряжения в точках оболочки не зависят от угловой координаты. Форма оболочки под давлением не меняется.

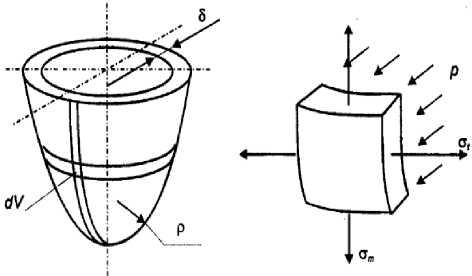
Рисунок 1. Расчетная схема тонкостенной оболочки

Figure 1. Calculation scheme of a thin-walled shell

При вырезании элемента оболочки двумя меридиональными (вдоль образующих) и двумя коническими сечениями (перпендикулярными поверхности оболочки) форма вырезанного элемента не меняется, меняются только размеры. Тогда касательные напряжения, которые вызывают изменение формы тела, на гранях элемента отсутствуют τ = 0, а нормальные напряжения σ – главные. Обозначим: σm – меридиональные напряжения (вдоль образующей оболочки), στ – тангенциальные (окружные) напряжения, σr – радиальные напряжения.

Как показывают практические расчеты, давление на тонкостенных оболочках, как правило, не превышают 10 атмосфер (1 МПа). При этом тангенциальные напряжения могут достигать величины σ τ = 100 МПа. Следовательно, радиальными напряжениями σ r можно пренебречь. В таком случае тонкостенная оболочка находится в плоском напряженном состоянии и напряжения по толщине оболочки не меняются [3].

Если нормальные напряжения по толщине оболочки переменные, то результатом действия напряжений будут продольное усилие N и изгибающий момент М .

Поскольку оболочка тонкостенная, напряжения по толщине оболочки можно считать постоянными. Результатом действия напряжений в этом случае будет действовать только продольное усилие N , а изгибающий момент М = 0 .

Рассмотрим равновесие элемента, вырезанного из оболочки двумя меридиональными и двумя коническими сечениями, перпендикулярными поверхности оболочки (рисунок 1) .

На этом рисунке р – давление жидкости или газа на оболочку; ρ m , dα m , σ m – соответственно, радиус кривизны, угол охвата, элемента и нормальное напряжение в меридиональном направлении; ρ l , dα l , σ l – то же самое в тангенциальном направлении.

Спроектируем все действующие силы на нормаль n к поверхности элемента.

Z F n = PdS dS

² ^lP m^d « m 3 sⁱⁿ

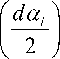
- ² ^ m Pl ^d «l sin

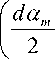
= 0

С учетом

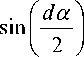
d a

и dS = p d a

получаем:

P Pl ^{d a}P m^{d a} m = ^{2 a} P m^{d a}5 . + ^{+ 2} ^ m Pl ^dai ^ d ^a m

Разделив это выражение на произведение толщины оболочки и радиусов кривизны в тангенциальном и осевом направлениях m и , находим окончательно уравнение связывающее важнейшие конструкционно-эксплутационные свойства оболочки [4].

^Z ₊ ^ m = P

P l   P m    ⁵

Уравнение такого вида называют уравнением Лапласа для тонкостенных оболочек. В записанном выражении две неизвестных величины – тангенциальное и осевое напряжения. Для того чтобы их найти необходимо второе уравнение. Его можно получить, записывая уравнение равновесия отсеченной части оболочки. Приравняем для этого сумму проекций на оси симметрии к нулю и получим [5]

Z F n = Z m 2 n r 5 cos( e ) - p n r ² - Q = 0,

Отсюда a = P + Q m 2nr cos(e), где Р – проекция сил внешнего давления на ось симметрии оболочки; Q – сила возможного внутреннего давления с обратным знаком.

Полученное соотношение трудно использовать при практической оценке технологических режимов процесса в силу достаточно большого количества допущений и неопределенности некоторых входящих величин, например внутреннего давления. Эти недостатки можно преодолеть, используя численные методы решения соответствующих уравнений. В рамках такого подхода решали плоскую упругопластическую задачу для сжатия кольца двумя сосредоточенными силами, моделируя приложенные нагрузки на отдельное зерно, за счет действия радиальных усилий в канале экспандера и свободную деформацию в перпендикулярном направлении (течение через кольцевой зазор).

Результаты и обсуждение

Численный анализ решений поставленной задачи осуществляли с помощь программы, составленной в пакете прикладных программ Mathcad, используя для решения уравнения Лапласа метод конечных элементов. В силу симметрии нагрузок относительно продольной оси единичного зерна (плоского кольца) задачу решали для одной четвертой его части (рисунок 2) .

Последовательно анализируя напряженно-деформированное состояние в каждой точке модели (рисунок 3) , методом обратной прогонки

устанавливали общую зависимость эффективность процесса экспандирования зерна от действующих технологических параметров [6].

расчет в системе Си у := coord z := coord

MIU := READPRN("Miufpm")

g2 := READPRN("gupm")

число узлов NU := max(MIU) NU = 66

число элементов NE := rows(MIU) NE = 100

у :- у 0.001

z 0.001

толщина кольца t :- 0.0057

Рассматриваем 1/4 кольца

11 узлов в ряду

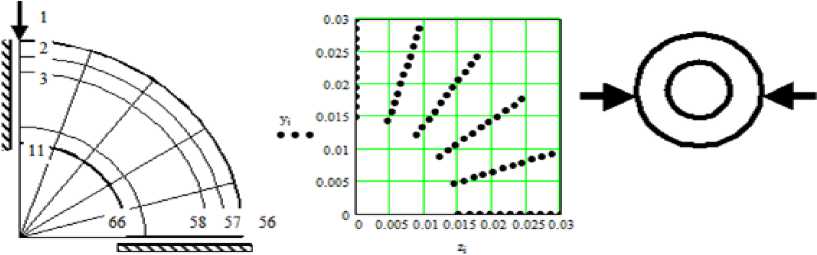
Рисунок 2. Фрагмент программы по формированию модели

Figure 2. Fragment of the program to build a model

for k е 1. NE for is 1.. 6

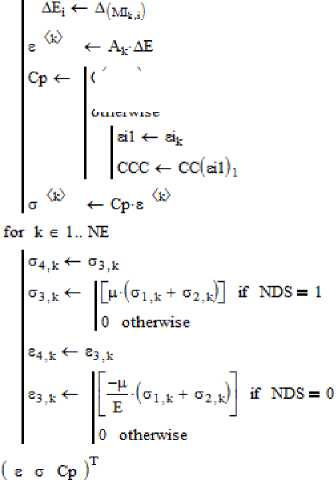
Рисунок 3. Один из расчетных блоков программы

Figure 3. One of the calculated blocks of the program

С(Е,ц) if klk= 0

otherwise

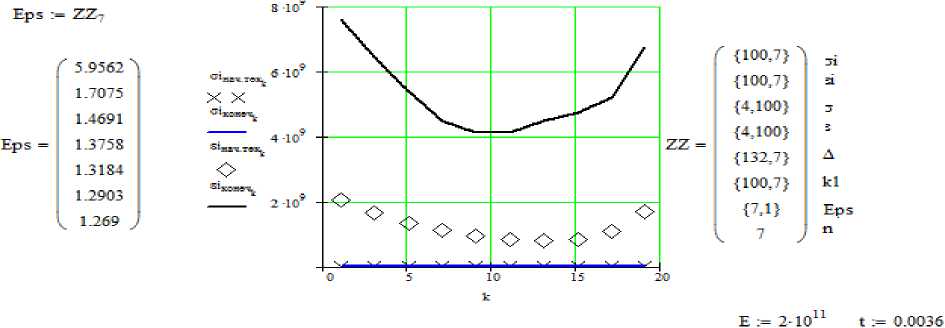
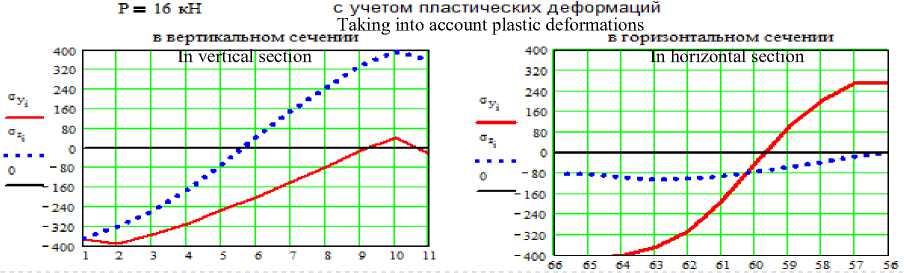
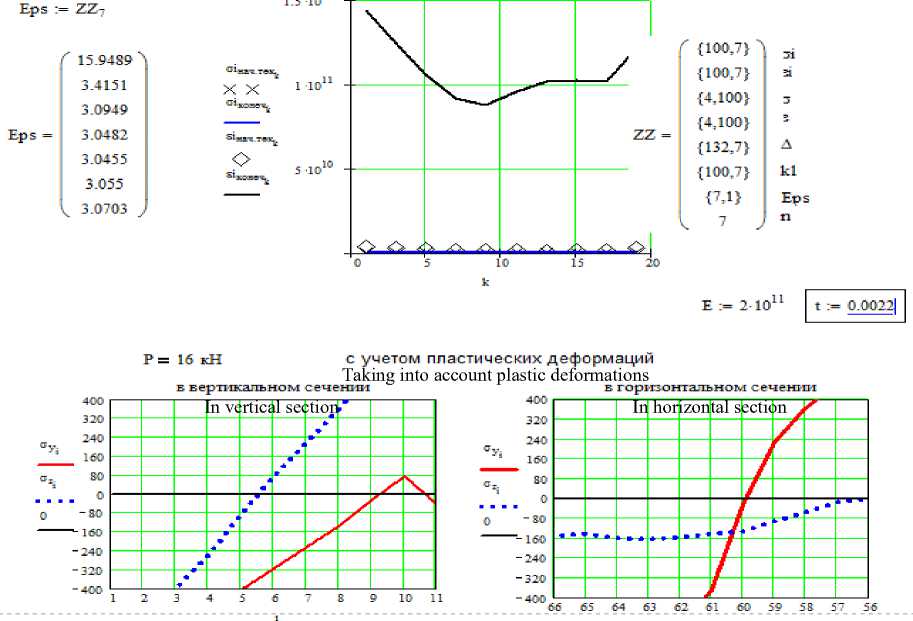
В процессе численного эксперимента выясняли каким образом влияют технологические режимы процесса экспандирования на его эффективность. Для этого проводили расчеты изменяя последовательно модуль упругости зерна и относительную толщину оболочки. На рисунке 4 и 5 приведены графические зависимости, характеризующие результаты расчетов. Кривые, изображенные на рисунке 4 свидетельствуют о практически неизменном характере изменения напряжений при увлажнении зерна и существенном снижении пределов текучести при сохранении экстремума в предполагаемой зоне разрушения между 10 и 15 участком в соответствии со схемой разбиения приведенной на рисунке 1. Графические зависимости рисунка 5 напротив говорят о существенном изменении характера напряженного состояния отдельных элементов поверхности зерна при уменьшении толщины оболочки, происходящей при дополнительной обработке зерна. Экстремум предела текучести также несколько меняет свое положение смещаясь ближе к зоне между 5 и 10 участком сетки конечных элементов [7–9].

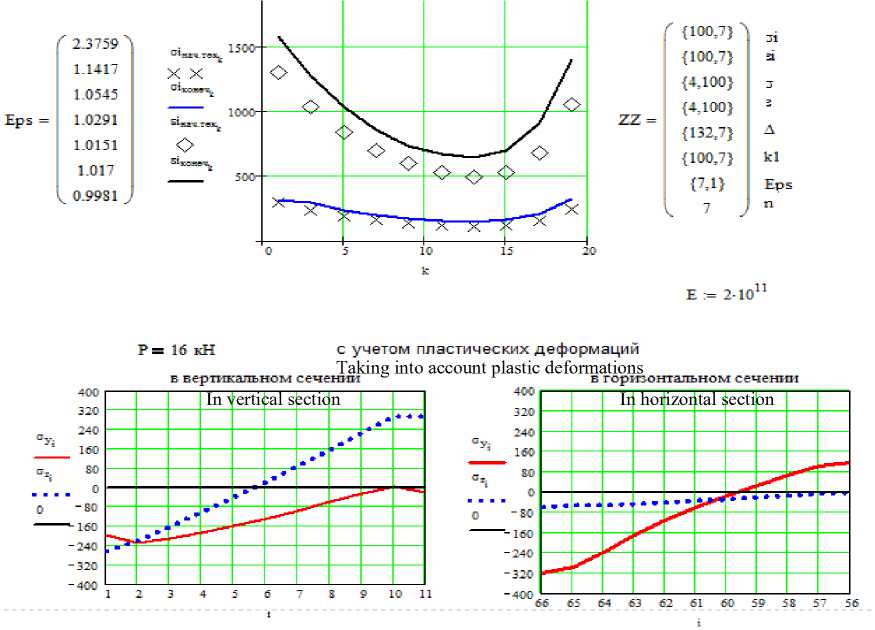
(а)

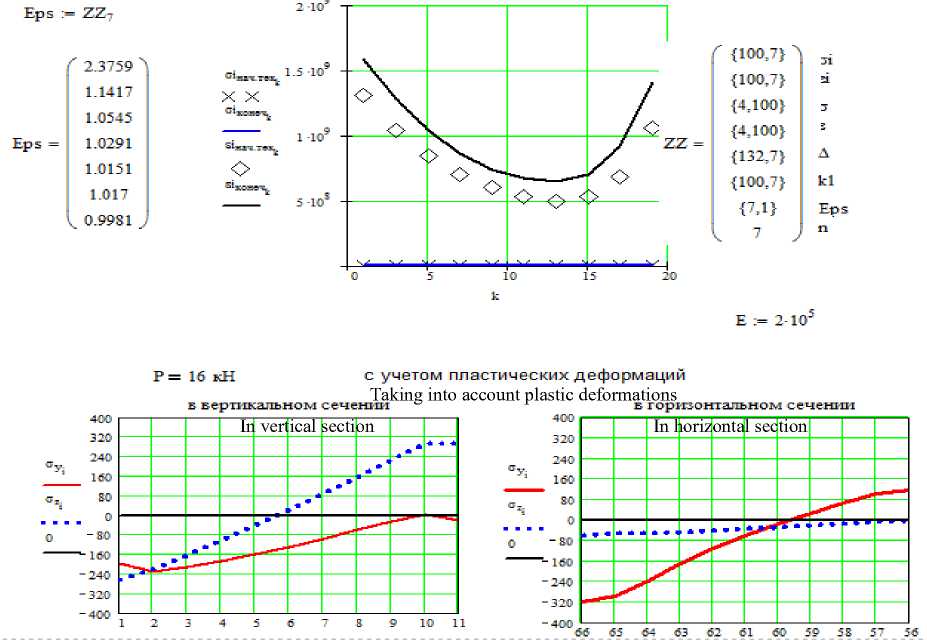
(b)

Рисунок 4. Характер изменения предела текучести при увлажнении зерна

Figure 4. The nature of the change in the yield point when the grain is moistened

(а)

(b)

Рисунок 5. Характер изменения напряжений в слоях при дополнительной сортировке зерна

Figure 5. The nature of the change in stresses in layers with additional sorting of grain

Выводы

Проведенное моделирование процесса экспандирования зерновых культур свидетельствует о том, что его эффективность существенным образом зависит от реализуемых технологических режимов таких, как влажность (с повышением влажности падает предел текучести при разрушении оболочки зерна) и толщина оболочки зерна (дополнительная его очистка перед обработкой). При этом следует отметить, что если в первом случае принципиально ход процесса