ЧИСЛЕННЫЙ АЛГОРИТМ ДЛЯ МИНИМАКСНОЙ ПОЛИНОМИАЛЬНОЙ АППРОКСИМАЦИИ ФУНКЦИЙ С ЗАДАННЫМ ВЕСОМ

Применение аппроксимаций функций, оптимальных по минимаксной (равномерной) норме, имеет существенные преимущества по сравнению с более простой аппроксимацией функций по методу наименьших квадратов [1, 2]. В качестве полезного инструмента при конструировании таких аппроксимаций используются полиномы Чебышева первого рода, наименее отклоняющиеся от нуля с весовой функцией, равной единице [3, 4]. Разложение функции в усеченный ряд, состоящий из полиномов, наименее отклоняющихся от нуля (в случае единичной весовой функции — полиномов Чебышева), является одним из способов приближенного конструирования полиномиальных аппроксимаций, оптимальных по минимаксной норме [4, 5]. Также для конструирования полиномиальных аппроксимаций, которые являются хорошим приближением к оптимальной минимаксной аппроксимации, используют аппроксимацию по дискретному набору коллокационных точек, соответствующих нулям полинома Чебышева со степенью на единицу больше, чем степень аппроксимирующего полинома [1, 2, 4, 5].

Такие способы характеризуются удобством и легкостью конструирования, а также определенными эмпирическими предпосылками получить на выходе достаточно хорошую точность. Однако упрощенные способы аппроксимации отличаются от истинной аппроксимации, оптимальной по минимаксной норме, и, следовательно, обеспечивают неконтролируемо бóльшую ошибку аппроксимации, чем точное решение соответствующей минимаксной оптимизационной задачи. Использование аппроксимаций, обеспечивающих для заданной функции точное решение минимаксной оптимиза- ционной задачи (когда это возможно), определенно более предпочтительно.

Множество функций, для которых имеется явное алгебраическое (аналитическое) представление для полиномиальной аппроксимации, являющейся оптимальной по минимаксной норме, не слишком велико (практически все такие случаи приводятся в [6–8]). В данной работе исследуется уточненный вариант быстро сходящегося численного алгоритма для определения коэффициентов полиномов, наименее отклоняющихся от заданной функции на заданном интервале с заданным весом, который ранее был рассмотрен в [9].

МИНИМАКСНАЯ АППРОКСИМАЦИЯ ФУНКЦИЙ И ТЕОРИЯ ЧЕБЫШЕВА

Постановка задачи

Пусть имеется непрерывная функция f(x) и конечный интервал [a, b], для которого задана непрерывная весовая функция ω(x), являющаяся строго положительной на этом интервале, за исключением, быть может, концов интервала, для которых она может обращаться в ноль.1 Требуется найти полином p(x) степени не выше n с заранее не- определенными коэффициентами a0, a1, a2, …, an:

p(x) = a0 + a1x + a2x2 + … + an-1xn-1 + anxn, (1) который является решением оптимизационной задачи max |ω(x) (f(x) – p(x))| → min, (2) где максимизация выполняется по переменной x ∈ [a, b], а минимизация выполняется по коэффициентам a0, a1, a2, …, an.

Без ограничения общности можно считать, что функция f ( x ) не является полиномом степени n или ниже, — в противном случае оптимальное решение для задачи (2) заранее известно и совпадает с функцией f ( x ).

Критерий Чебышева для минимаксной полиномиальной аппроксимации

Для того чтобы полином p ( x ) степени n был решением задачи (2), необходимо и достаточно, чтобы существовали такой набор из n + 2 точек x 0 < x 1 < x 2 < … <  x n + 1 , принадлежащих интервалу [ a , b ], и такое число ε (положительное либо отрицательное), чтобы были выполнены условия:

–| ε | ≤ ω( x ) ( f ( x ) – p ( x )) ≤ | ε | при x ∈ [ a , b ], (3) ω( x k ) ( f ( x k ) – p ( x k )) = (–1) ^k ε при k = 0, 1, .., n + 1. (4)

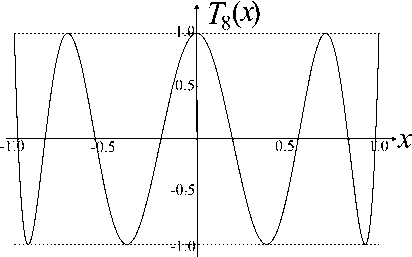
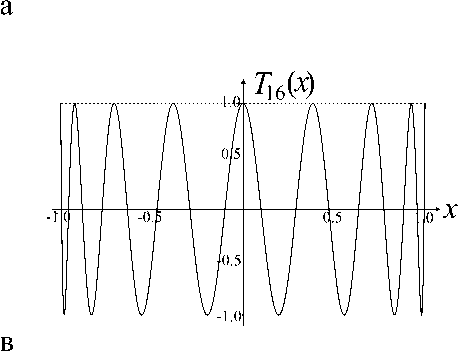
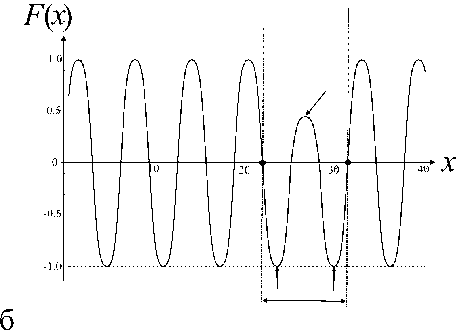
Точки x 0 <  x 1 <  x 2 < … <  x n + 1 с чередующимися положительными минимумами и отрицательными максимумами, равными по абсолютной величине максимуму модуля исследуемой функции, называются альтернансом Чебышева (см. [7, 8, 10–14]). Графики полиномов Чебышева первого рода [3], демонстрирующие выполнение данного условия на интервале [–1, +1] с весом ω( x ) = 1, приводятся на рис. 1.

Смысл условий (3), (4) состоит в том, что для полинома p ( x ) имеется набор из n + 2 пробных точек x k , в которых невязка ω( x ) ( f ( x ) – p ( x )) имеет локальные чередующиеся отрицательные минимумы и положительные максимумы, равные ± | ε |, причем значения этих минимумов и максимумов являются глобальными на интервале [ a , b ]. Этот критерий является частным случаем теории Чебышева минимаксной аппроксимации функций с помощью дробно-рациональных функций [7, 8], однако в случае аппроксимации с помощью полиномов доказательство соответствующих утверждений упрощается.

Утверждение 1 (теорема Валле – Пуссена [7, 8, 15–17]). Если рассматриваемая функция ω( x ) ( f ( x ) – – p ( x )) для некоторого многочлена p ( x ) степени n принимает в N последовательных точках x 0 <  x 1 < … <  x N – 1 интервала [ a , b ] отличные от нуля значения λ 0 , λ 1 , …, λ N – 1 с чередующимися

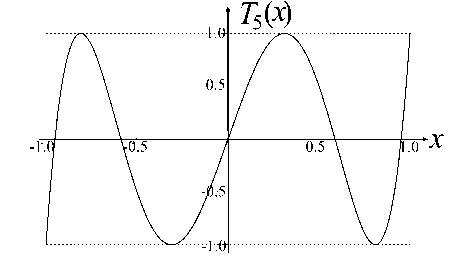
б

Рис. 1. Полиномы Чебышева T n ( x ), которые наименее отклоняются от нуля на отрезке [–1, +1].

а — n = 5, б — n = 8, в — n = 16

знаками, где N > n + 2, то для любого другого многочлена r(x) степени n справедливо max |и(x) (f(x) - r(x))| > min {|Xo|, |Xt|, ..., |Xn—1|}.

Доказательство . Пусть имеется многочлен r ( x ), для которого выполняется условие max |ω( x ) ( f ( x ) – r ( x ))| < min (|λ 0 |, |λ 1 |, …, |λ N – 1 |). Будем считать, что в последовательности x k для четных точек значения ω( x k ) ( f ( x k ) – r ( x k )) строго положительные, а для нечетных точек строго отрицательные. (Когда для нечетных точек значения положительные, а для четных точек отрицательные, рассуждения аналогичны.) Это означает, что в четных точках x k выполнено условие ω( x k ) ( f ( x k ) – – r ( x k )) < |λ k | = ω( x k ) ( f ( x k ) – p ( x k )), а в нечетных точках x k выполнено условие ω( x k ) ( f ( x k ) – r ( x k )) > > –|λ k | = ω( x k ) ( f ( x k ) – r ( x k )). В результате величина ω( x ) ( p ( x ) – r ( x )) строго отрицательна в четных точках x k и строго положительна в нечетных точках x k . Значения весовой функции ω( x k ) в точках x k , для которых функция ω( x ) ( f ( x ) – r ( x )) принимает строго положительные или строго отрицательные значения, не обращаются в ноль и, следовательно, строго положительны. Следовательно, не равный тождественно нулю многочлен p ( x ) – r ( x ) степени n попеременно принимает строго положительные и строго отрицательные значения как минимум в n + 2 разных точках и в силу этого имеет не менее n + 1 нулей кратности 1. Значит, многочлен r ( x ), для которого выполняется условие max |ω( x k ) ( f ( x k ) – r ( x k ))| < min (|λ 0 |, |λ 1 |, …, |λ N – 1 |), не существует.

Замечание. Теорема Валле – Пуссена позволяет получить для решения оптимизационной задачи (2) оценку снизу. Если λ 0 , λ 1 , …, λ N – 1 — это локальные максимумы и минимумы функции ω( x ) ( f ( x ) – r ( x )) с чередующимися знаками, то такая конструкция называется альтернансом Валле – Пуссена, и для решения оптимизационной задачи (2) она дает не только оценку снизу, но и оценку сверху, равную max {|λ 0 |, |λ 1 |, …, |λ N –1 |}.

Утверждение 2. Если для полинома p ( x ) выполнены условия (3), (4) критерия Чебышева, то оптимальное значение для правой части оптимизационной задачи (2) равно | e |, а полином p ( x ) является ее решением (возможно, одним из многих).

Доказательство . Альтернанс Чебышева (3), (4) является частным случаем альтернанса Валле – Пуссена, поэтому, согласно Утверждению 1, правая часть оптимизационной задачи (2) не меньше | e |. C другой стороны, max | и( x ) (f(x ) - p ( x ))| = | e |. Следовательно, минимум оптимизационной задачи (2) равен |e|, а полином p ( x ) является одним из ее решений.

Утверждение 3. Существует полином p ( x ), который обеспечивает решение оптимизационной задачи (2). (Это исключает вариант, когда есть полиномы p_k ( x ) со все более и более уменьшающимися значениями для P k = max | ω( x ) ( f ( x ) – p k ( x ))|, в то время как минимум этой величины никогда не достигается на множестве полиномов заданной степени.)

Доказательство. Значения величин Pk = = max |ω(x) (f(x) – pk(x))| ограничены снизу нулем, поэтому для значений Pk на множестве полиномов существует точная нижняя грань P. В соответствии с определением точной нижней грани существует последовательность полиномов pk(x) степени n: pk(x) = a0, k + a1, k x + a2, k x2 + … + an – 1, k xn – 1+an, k xn, для которой lim Pk = P при k ^ да. Следовательно, начиная с некоторого номера k значения многочленов pk(x) на интервале [a + δ, b – δ], где δ достаточно мало, будут ограничены сверху и снизу (от концов интервала пришлось сделать отступ, чтобы учесть случай, когда весовая функция на концах интервала может быть равна нулю). Из формулы Лагранжа [1, 2] для полинома степени n, который в n + 1 заданных точках xk принимает значения yk

г

p ( x ) = S Уз П

j = 1, n + 1

^     i = 1, П + 1, i * j

^{( x -} x ) ' ⁽ x j ^- x ) ^

следует, что когда в n + 1 фиксированных точках x k значения полинома y k ограничены сверху и снизу, то каждый из коэффициентов полинома также ограничен сверху и снизу. Следовательно, в соответствии с теоремой Больцано – Вейерштрасса (иначе называемой леммой Больцано – Вейершт-расса) о предельной точке, согласно которой из всякой бесконечной ограниченной последовательности точек пространства Rⁿ можно выделить сходящуюся подпоследовательность, в последовательности полиномов p k ( x ) можно выбрать подпоследовательность полиномов, в которой для каждого из коэффициентов полинома имеется предел. То есть имеется такая последовательность полиномов p_k ( x ), для которой lim P_k = P при k ^ да , а у коэффициентов полиномов имеются предельные значения b j = lim a j , _k при k ^ да .

Рассмотрим полином r ( x ) с коэффициентами b j : r ( x ) = b 0 + b 1 x + b 2 x ² + … + b n – 1 x^{n – 1} + b n xⁿ .

Поскольку bj = lim ajk, то для любого фиксированного значения x выполнится условие lim pk(x) = r(x) при k ^ да, причем стремление к пределу является равномерным на рассматри- ваемом конечном интервале значений x. Из неравенства max |ω(x) (f(x) – r(x))| ≤ max |ω(x) (f(x) – pk(x))| + + max |ω(x)| max |r(x) – pk(x)| следует, что max |ω(x) (f(x) – r(x))| = P, т.к. меньше, чем P, эта величина быть не может, в то время как при k → ∞ первое слагаемое в правой части стремится к P, а второе слагаемое стремится к нулю. Это означает, что для полинома r(x) величина (2) достигает своей нижней границы.

Утверждение 4 (теорема Чебышева). Полином p ( x ), обеспечивающий решение оптимизационной задачи (2), удовлетворяет критерию Чебышева.

Доказательство. Рассмотрим поведение функции F(x) = ω(x) (f(x) – p(x)) на отрезке [a, b]. Для упрощения рассуждений будем считать, что число интервалов, на которых функция F(x) меняет знак, конечно. Это не означает, что число нулей функции F(x) также конечно — допустим вариант, когда функция F(x) равна нулю в любой точке некоторого интервала внутри отрезка [a, b]. Пусть точки y1, y2, …, ym разбивают отрезок [a, b] на m + 1 интервалов, на каждом из которых функция F(x) принимает попеременно то положительное, то отрицательное значение, причем допустим вариант, когда на всем отрезке [a, b] функция F(x) принимает только положительные или только отрицательные значения. Если имеется непрерывный ин- тервал, целиком состоящий из нулей функции F(x), этот интервал присоединяется к соседнему интервалу с положительными либо отрицательными значениями функции.

Для интервалов с положительными значениями F ( x ) выбираем точку с максимальным значением функции на этом интервале (возможно, не единственную на этом интервале), а для интервалов с отрицательными значениями F ( x ) выбираем точку с минимальным значением функции на этом интервале. Получаем набор точек y 1 , y 2 , …, y m , — нулей функции F ( x ), разбивающих отрезок [ a , b ] на m + 1 интервалов, для которых функция F ( x ) сохраняет свой знак, изменяя его при переходе через границу интервала, и набор принадлежащих этим интервалам точек x 0 , x 1 , x 2 , …, x m , x m + 1 , не совпадающих с концами интервалов, который состоит из чередующихся положительных максимумов и отрицательных минимумов λ 0 , λ 1 , λ 2 , …, λ m + 1 функции F ( x ) (альтернанс Валле – Пуссена и прилагающееся к нему разбиение отрезка [ a , b ] на интервалы, на которых функция F ( x ) сохраняет знак) .

Пусть λ = max |λ k |. Если на каком-то интервале максимум равен λ, а на соседнем (последующем или предшествующем) интервале модуль минимума меньше λ, то этот интервал вместе с последующим интервалом с положительным максимумом, независимо от его значения, присоединяется к текущему интервалу (см. рис. 2, а).

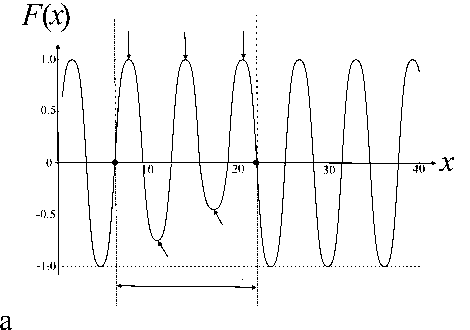
Рис. 2 . Объединение отрезков с чередующимися максимумами и минимумами.

а — случай одиночного минимума или нескольких последовательно расположенных минимумов, которые лежат выше минимального уровня функции F ( x ); б — случай одиночного максимума или нескольких последовательно расположенных максимумов, которые лежат ниже максимального уровня функции F ( x ).

Вертикальными стрелками отмечены минимумы и максимумы, которые соответствуют максимальному отклонению. Наклонными стрелками отмечены минимумы и максимумы, которые по модулю меньше максимального отклонения, так что график функции можно сдвинуть вниз или соответственно вверх на ненулевое расстояние, не выходя за границы максимального отклонения. Жирными точками отмечены нули функции F ( x ), являющиеся границей комбинированного интервала со строго положительными либо со строго отрицательными максимальными отклонениями функции F ( x )

Новый интервал обладает тем свойством, что из функции F ( x ) можно вычесть такую положительную константу, чтобы положительный максимум функции на интервале уменьшился, но при этом абсолютное значение отрицательного минимума функции на интервале не настолько увеличилось, чтобы превысить новый максимум функции.

Точно так же если на каком-то интервале минимум равен –λ, а на соседнем интервале максимум меньше λ, то этот интервал вместе с последующим интервалом, содержащим отрицательный минимум, присоединяется к текущему интервалу (см. рис. 2, б). В этом случае на полученном интервале к функции F ( x ) можно прибавить такую положительную константу, чтобы уменьшилось абсолютное значение отрицательного минимума на интервале, но при этом не настолько увеличился положительный максимум функции на интервале, чтобы он стал больше абсолютного значения нового минимума.

В конечном итоге на интервале [ a , b ] для заданного полинома p ( x ) будет получен набор из N интервалов и принадлежащих им точек x 0 , x 1 , x 2 , …, x N – 1 с чередующимися положительными максимумами и отрицательными минимумами функции F ( x ), равными ±λ , где λ = max | ω( x ) ( f ( x ) – – p ( x ))|. Если N больше или равно n + 2, то такой полином p ( x ) удовлетворяет критерию Чебышева и, в соответствии с Утверждением 1, будет решением оптимизационной задачи (2).

Пусть N меньше или равно n + 1. На этапе объединения интервалов был получен набор точек y 1 , y 2 , …, y N – 1 (границы интервалов), в которых функция F ( x ) обращается в ноль и меняет свой знак. Эти точки разбивают интервал [ a , b ] на интервалы меньшего размера, на каждом из которых имеется точка с чебышевским минимумом или чебышевским максимумом. Также имеются константы δ k > 0, которые можно вычитать из функции F ( x ) на интервалах с положительными максимумами или прибавлять к функции F ( x ) на интервалах с отрицательными минимумами, уменьшая при этом минимаксную норму на соответствующем интервале.

Без ограничения общности можно считать, что на первом интервале функция F ( x ) принимает положительные значения, — когда это не так, можно изменить знак одновременно у функции f ( x ) и у полинома p ( x ), не меняя оптимизационную задачу (2).

Рассмотрим функцию Ω( x ), которая представляет собой произведение полинома степени не выше n и весовой функции ω( x ):

Ω( x ) = ω( x ) ( y 1 – x ) ( y 2 – x )…( y N – 1 – x ).

Функция Ω(x) строго положительна на тех интер- валах, на которых имеется чебышевский максимум функции F(x), и строго отрицательна на тех интервалах, на которых имеется чебышевский минимум функции F(x). Если вычесть из функции F(x) функцию sΩ(x) с достаточно малым положительным множителем s (например, можно выбрать s = (δ / R), где R = max |Ω(x)|, а δ = min δk > 0), это безопасным образом уменьшит положительные максимумы функции F(x) и уменьшит отрицательные минимумы функции F(x), тем самым уменьшив величину max |F(x)|. Следовательно, такой полином p(x) не может быть решением для оптимизационной задачи (2), поскольку можно получить еще меньшее значение для max |F(x)| при замене текущего полинома p(x) степени n на новый полином r(x) степени n:

G(x) = F ( x ) – (δ / R ) Ω( x ) =

= ω( x ) ( f ( x ) – p ( x )) – (δ / R ) ω( x ) ( y 1 – x )…( y N – 1 – x ) =

= ω( x ) ( f ( x ) – p ( x ) – (δ / R ) ( y 1 – x )…( y N – 1 – x )) =

= ω(x) (f(x) – r(x)), max |G(x)| < max |F(x)|.

Вывод: оптимальный полином степени n , рассмотренный в Утверждении 2, обязан удовлетворять критерию Чебышева.

Утверждение 5. Полином p ( x ), удовлетворяющий критерию Чебышева и обеспечивающий решение оптимизационной задачи (2), является единственным.

Доказательство. Идея доказательства заимствована из [7, 8]. Пусть имеются два полинома p(x) и r(x) степени n, которые являются решением оптимизационной задачи (2). Для вырожденного случая, для которого max |ω(x) (f(x) – p(x))| = 0 и max |ω(x) (f(x) – r(x))| = 0, должны выполняться условия f(x) – p(x) ≡ 0 и f(x) – r(x) ≡ 0, — что означает, что p(x) ≡ r(x). Поэтому будем считать, что max |ω(x) (f(x) – p(x))| = max |ω(x) (f(x) – r(x))| > 0, так что у выражений ω(x) (f(x) – p(x)) и ω(x) (f(x) – – r(x)) на интервале [a, b] имеются не равные нулю максимумы и минимумы.

В соответствии с Утверждением 3, каждый из полиномов p(x) и r(x) удовлетворяет критерию Чебышева, причем значение ε ≠ 0 для них одно и то же. Пусть x1, x2, …, xn + 2 — это чебышевские точки уклонения с чередующимися максимумами и минимумами, равными ±ε, для функции F(x) = ω(x) (f(x) – p(x)). Если для полинома r(x) функция G(x) = ω(x) (f(x) – r(x)) принимает в точ- ках x1, x2, …, xn + 2 те же самые значения ±ε, кроме, может быть, одной точки из этого списка, то полиномы p(x) и r(x) тождественно равны друг другу. Действительно, в этом случае разность

d ( x ) = F ( x ) – G ( x ) =

= ω( x ) ( f ( x ) – p ( x )) – ω( x ) ( f ( x ) – r ( x )) =

= ω( x ) ( r ( x ) – p ( x )),                             (5)

которая представляет собой произведение положительной весовой функции ω( x ) и полинома степени не выше n , обращается в ноль в n + 2 точках или, в крайнем случае, в n + 1 точке, — и поэтому полином r ( x ) – p ( x ) обязан быть тождественным нулем, поскольку иначе не объяснить наличия у него такого количества нулей (весовая функция ω( x ), даже если она обращается в ноль на концах интервала [ a , b ], не равна нулю в точках минимумов и максимумов функции F ( x )).

Пусть среди чебышевских точек уклонения x 1 , x 2 , …, x n + 2 для функции F ( x ) имеются хотя бы две точки x k и x k + m , в которых значение функции G ( x ) не совпадает со значением функции F ( x ) в этих точках (минимумом либо максимумом функции F ( x )). Требуется доказать, что в таком случае внутри интервала [ x k , x k + m ] найдется по крайней мере еще одна точка, не совпадающая с точками x 1 , x 2 , …, x n + 2 , в которой значения функций F ( x ) и G ( x ) совпадают (хотя, возможно, в этой точке общее значение функций F ( x ) и G ( x ) и не равно ±ε ), — а следовательно, у функции d ( x ), заданной формулой (5), имеется дополнительный неучтенный ноль.

Если в какой-то точке x j выполнено условие d ( x j ) ≠ 0, то знак разности d ( x j ), заданной формулой (5), совпадает со знаком F ( x j ). Действительно, если x j это точка отрицательного минимума функции F ( x ), то G ( x j ) ≥ F ( x j ), а если x j это точка положительного максимума функции F ( x ), то G ( x j ) ≤ F ( x j ). Если

d ( x k ) ≠ 0, d ( x k + 1 ) = 0, d ( x k + 2 ) = 0, …, d ( x k + m –1 ) = 0, d ( x k + m ) ≠ 0,                                          ⁽⁶⁾

то выражения (–1)k F(xk) и (–1)k + m F(xk + m) имеют одинаковые знаки и, следовательно, одинаковые знаки имеют выражения d(xk) и (–1)m d(xk + m). Следовательно, четность числа перемен знака функции d(x) на интервале [xk, xk + m] совпадает с четностью числа m, а тем самым и четность числа корней (с учетом их кратности) для функции d(x) на интервале [xk, xk + m] совпадает с четностью числа m. Согласно (6) у функции d(x) на интервале [xk, xk + m] имеется как минимум m – 1 не равных друг другу корней и, следовательно, либо должен существовать еще один корень, либо один из корней xk + 1, xk + 2, …, xk + m – 1 имеет четную кратность, как минимум равную двум. Проделав эту операцию для всех интервалов, ограниченных точками xk с ненулевыми значениями d(xk), получим, что число корней функции d(x) на интервале [a, b] с учетом кратности корней будет не меньше, чем n + 1. Следовательно, в формуле d(x) = ω(x) (r(x) – p(x)) полином r(x) – p(x), имеющий степень не выше n, обязан быть тождественным нулем.

АЛГОРИТМ КОНСТРУИРОВАНИЯ МИНИМАКСНОЙ ПОЛИНОМИАЛЬНОЙ АППРОКСИМАЦИИ ФУНКЦИИ

Из критерия Чебышева для минимаксной аппроксимации функции выводится алгоритм численного построения аппроксимирующих полиномов, который представляет собой измененный и оптимизированный алгоритм Е.Я. Ремеза [18– 22]:

• 1.    Произвольным образом выбирается начальный набор точек x 0 <  x 1 <  x 2 < …< x n + 1 , принадлежащих интервалу [ a , b ]. Если весовая функция ω( x ) обращается в ноль в точке x = a , необходимо обеспечить выполнение условия a <  x 0 . Если весовая функция ω( x ) обращается в ноль в точке x = b , необходимо обеспечить выполнение условия x 0 <  b .

• 2.    Для текущего набора точек a ≤ x 0 <  x 1 < <  x 2 < …< x n + 1 ≤ b конструируется вспомогательная функция g ( x ) = a ⋅ f ( x ) – p ( x ), где a это некоторая константа, а p ( x ) — полином степени n с некоторыми коэффициентами. Свободные коэффициенты функции g ( x ), т.е. множитель a и коэффициенты полинома p ( x ), выбираются так, чтобы были выполнены условия ω( x k ) g ( x k ) = (–1) ^k при k = 0, 1, …, n + 1. Такая функция существует и определяется единственным образом (см. далее).

• 3.    Теперь надо определить корни алгебраического уравнения g ( x ) = 0, которые находятся на интервале [ a , b ]. Поскольку на краях интервалов [ x k , x k + 1 ] значения функции g ( x ) имеют разные знаки, то внутри каждого такого интервала существует по крайней мере один корень уравнения g ( x ) = 0. Если функция f ( x ) меняется достаточно медленно, то на каждом из интервалов [ x k , x k + 1 ] имеется ровно один корень кратности единицы, а численное определение этих корней не представляет трудности. Если же это условие нарушается и на рассматриваемом интервале имеется несколько корней, все эти корни добавляются к списку (кратные корни с четной кратностью, для которых значения функции g ( x ) по обе стороны от корня имеют один и тот же знак, в список не включаются). По завершении работы по поиску корней к списку значений a <  y 1 <  y 2 < …< y m <  b , являющихся корнями нечетной кратности функ-

• ции g(x) на интервале [a, b], добавляются начало и конец интервала y0= a и ym + 1 = b.

• 4.    Теперь интервал [ a , b ] представляет собой совокупность не менее чем n + 2 интервалов [ y k , y k + 1 ], которые соприкасаются своими конечными точками, причем на каждом интервале функция g ( x ) сохраняет знак, а при пересечении границы между интервалами знак функции меняется. Рассмотрим функцию G ( x ) = ω( x ) g ( x ), которая на интервале [ a , b ] принимает значения того же знака, что и функция g ( x ). Найдем для функции G ( x ) на каждом интервале x ∈ [ y k , y k +1 ] глобальный (для рассматриваемого интервала) экстремум G k и точку z k ∈ [ y k , y k + 1 ], в которой расположен этот экстремум. Для интервалов с положительными значениями функции G ( x ) надо искать положительный максимум, а для интервалов [ y k , y k + 1 ] с отрицательными значениями функции — отрицательный минимум.

• 5.    Если число найденных точек G k = G ( z k ), z k ∈ [ y k , y k + 1 ] с чередующимися знаками больше n + 2, необходимо исключить лишние точки. Для этого выбирается наименьшее по модулю значение G k . Если интервал с этим значением первый либо последний в списке, значение G_k и соответствующая этому значению точка z k отбрасываются. Если интервал с этим значением находится в середине списка, надо проверить предшествующий и последующий интервалы и отбросить не только рассматриваемое значение G k , но также и то из двух соседних значений G k – 1 и G k + 1 , которое будет меньше по модулю. Действительно, знаки значений G k – 1 и G k + 1 противоположны по знаку значению G k , а т.к. из-за удаления из списка значения G k два значения одного знака окажутся рядом, то из двух значений G k + 1 и G k – 1 одно надо отбросить. Важно: поскольку на каждом шаге удаляется одна либо две точки, то есть риск из n + 3 точек z k получить сразу n + 1 точек, вместо требуемых n + 2 точек, — в этом случае следует оставить точку G_k в списке, а вместо нее удалить ту из начальной и конечной точек, которая меньше по модулю. Процесс продолжается, пока в списке не окажется n + 2 экстремумов G k = G ( z k ), которым соответствуют n + 2 точек z k с чередующимися положительными максимумами и отрицательными минимумами функции G ( x ) = ω( x ) g ( x ).

• 6.    Для имеющегося списка точек a ≤ z 0 <  z 1 < <  z 2 < …< z n + 1 ≤ b рассмотрим более внимательно значения экстремумов G k = ω( z k ) g ( z k ) = (–1) ^k ε k . Если в пределах заданной точности ε k ≈ 1, то полином, удовлетворяющий требованиям критерия Чебышева, найден. При этом из теоремы Валле – Пуссена о наилучшем приближении функции полиномами (Утверждение 1) следует, что точный оптимум для задачи (2) лежит в диапазоне между min | ε k / a | и max | ε k / a | (где a это множитель в вы-

• ражении g(x) = a⋅f(x) – p(x)). Если же условие εk ≈ 1 не выполнено, заменяем пробные точки a ≤ x0 < < x1 < x2 < …< xn + 1 ≤ b на точки a ≤ z0 < z1 < z2 < …< zn + 1 ≤ b и возвращаемся к шагу 2.

• 7.    Остается нормировать функцию g ( x ) = = a ⋅ f ( x ) – p ( x ) так, чтобы коэффициент при функции f ( x ) стал равен единице. Такая нормировка всегда осуществима, поскольку коэффициент a не может быть нулем, — иначе окажется, что имеется отличный от тождественного нуля полином p ( x ) степени n , у которого есть n + 1 корней, находящихся между соседними максимумами и минимумами разных знаков в количестве n + 2 штук.

Очевидно, что если этот алгоритм сходится, то он сходится к полиному, удовлетворяющему критерию Чебышева, и тем самым результат работы алгоритма является решением оптимизационной задачи (2), причем единственным таким решением. Теоретически алгоритм сходится всегда, причем со скоростью геометрической прогрессии: для любой непрерывной весовой функции и для любой степени n найдутся такие числа C > 0 и 0 < λ < 1, для которых max |ω(x) (ai⋅f(x) – pi(x))| ≤ 1 + Cλi, где i это номер итерации. Доказательство аналогично доказательству сходимости алгоритма Е.Я. Ремеза в монографии [20]. К сожалению, из-за ошибок округления алгоритм может расходиться для "плохих" функций f(x) и ω(x), — а именно для функций, которые не меняются медленно на интервале [a, b], а вместо этого демонстрируют многочисленные осцилляции, так что для них имеется более одного корня для интервалов [xk, xk + 1] или более одного локального максимума или минимума для интервалов [yk, yk + 1]. В таких случаях алгоритм может выполнять бесконечный цикл, фактически переключаясь между одним и тем же списком тестируемых полиномов. Такое поведение алгоритма следует контролировать вручную, задавая максимальное количество циклов, которое разрешено выполнить. Другим полезным критерием для прекращения работы алгоритма, попавшего в бесконечный цикл, может быть проверка возрастания на очередном шаге разброса между максимумами и минимумами ±εk, найденными на интервалах [yk, yk + 1], по сравнению с этой величиной для предыдущего шага. Также подозрительным признаком, сигнализирующим о зацикливании алгоритма, может быть регулярное возникновение ситуации, когда на шаге 5 при "чистке" точек Gk на каком-то шаге в списке оказывается меньше чем n + 2 точки и возникает необходимость сделать шаг назад, удалив первую или последнюю точку, — ведь даже если оптимальным многочленом p(x) является тождест- венный ноль (например, такая ситуация возникает при попытке аппроксимации на интервале [0, 1] многочленом конечной степени функции sin(1 / x)), то, согласно Утверждению 4, все равно должен существовать набор из n + 2 точек zk, которые формируют альтернанс Чебышева.

Так как весовая функция ω( x ) на каком-то из концов интервала [ a , b ] может обращаться в ноль, то для выполнения шага 2 потребуется, чтобы пробные точки, выбираемые на шаге 1, лежали строго внутри интервала [ a , b ]: a <  x 0 <  x 1 < <  x 2 < …< x n +1 <  b . Можно убедиться, что если ω( a ) = 0 либо ω( b ) = 0 и при этом a < x 0 <  x 1 <  x 2 < …< x n +1 <  b , то условие a <  x 0 <  x 1 <  x 2 < …< x n +1 < <  b сохранится для всех последующих итераций, т.к. точки z k на шаге 6 также должны будут удовлетворять условию a <  z 0 <  z 1 <  z 2 < …< z n + 1 <  b .

Для вычисления коэффициентов на шаге 2 нельзя применять явное решение системы линейных уравнений для нахождения коэффициентов функции g ( x ) = a ⋅ f ( x ) – p ( x ), поскольку обусловленность матрицы линейных уравнений (за исключением первого столбца, совпадающая с матрицей Вандермонда) быстро растет с увеличением степени полинома — в результате малые ошибки округления чисел с плавающей точкой приводят к совершенно неудовлетворительным значениям для неизвестных коэффициентов. Один из работоспособных способов нахождения искомой функции g ( x ) = a ⋅ f ( x ) – p ( x ) на шаге 2 состоит в следующем. Из условий p ( x k ) = a ⋅ f ( x k ) – (–1) ^k / ω( x k ), которые равносильны условиям ω( x k ) ( a ⋅ f ( x k ) – – p ( x k )) = (–1) ^k , при k = 0, 1, …, n по формуле Ла-гранжа ² [1, 2] находятся коэффициенты полинома p ( x ), который в заданных точках x k принимает заданные значения. Эти коэффициенты будут представлять собой линейные выражения со свободным коэффициентом a . После этого для уравнения ω( x k ) ( a ⋅ f ( x k ) – p ( x k )) = (–1) ^k при k = n + 1, которое представляет собой линейное уравнение относительно переменной a , находится неизвестный коэффициент a .

Другой, более эффективный способ определения коэффициента a и коэффициентов полинома p ( x ), для которых на шаге 2 будут выполнены условия

ω(xk) (a⋅f(xk) – p(xk)) = (–1)k при k = 0, 1, .., n+1, состоит в следующем. Для выполнения равенств p(xk) = a⋅f(xk) – (–1)k / ω(xk) по схеме конечных раз- ностей Ньютона [1, 2] определяются такой полином r(x), для которого выполнены условия r(xk) = = (–1)k / ω(xk) при k = 0, 1, …, n, и полином s(x), для которого выполнены условия s(xk) = f(xk) при k = 0, 1, …, n. Затем из условия

ω( x n + 1 ) ( a ⋅ f ( x n + 1 ) – a ⋅ s ( x n + 1 ) + r ( x n + 1 )) = (–1) ^{n + 1}

определяется константа a . После этого искомый полином p ( x ) определяется в соответствии с формулой p ( x ) = a ⋅ s ( x ) – r ( x ). Этот способ можно использовать также в следующем виде: вычисляются полином s ( x ) степени n + 1, для которого в точках x k при k = 0, 1, …, n + 1 выполнены условия s ( x k ) = f ( x k ), и полином r ( x ) степени n + 1, для которого в точках x k при k = 0, 1, …, n + 1 выполнены условия r ( x k ) = (–1) ^k / ω( x k ). Остается подобрать коэффициент a так, чтобы полином a ⋅ s ( x ) – r ( x ) имел степень n, — что всегда возможно, если только функция f ( x_k ) не является полиномом степени не выше n .

Отметим, что на промежуточных этапах нет необходимости определять коэффициенты полинома p ( x ) в явном виде, достаточно уметь вычислять его значение в произвольной точке. Поэтому при компьютерной реализации данного алгоритма вплоть до получения итогового результата можно использовать вычисление значений полинома p ( x ) по формуле p ( x ) = a ⋅ s ( x ) – r ( x ), где для вспомогательных полиномов s ( x ) и r ( x ) используется форма конечных разностей Ньютона .

Для улучшения работы алгоритма на начальном этапе на шаге 1 рекомендуется выбирать для начальных точек a ≤ x 0 <  x 1 <  x 2 < …< x n + 1 ≤ b нули полинома Чебышева первого рода степени n + 2, смещенные и масштабированные с интервала [–1, +1] к интервалу [ a , b ]. На шаге 2 вместо условия ω( x k ) p ( x k ) = (–1) ^k рекомендуется использовать условие ω( x k ) p ( x k ) = (–1) ^{k ⋅} (4 / ( b – a )) ^{– n – 1} , чтобы избежать неоправданно больших коэффициентов у полинома p ( x ) и функции f ( x ) (такой выбор масштаба соответствует осцилляциям полинома Чебышева степени n + 1, пересчитанного от интервала [–1, +1] к интервалу [ a , b ] и масштабированного так, чтобы старший коэффициент был равен единице).

Пример. Пусть f ( x ) = exp( x ), a = 0, b = 1, ω( x ) = 1. Для n = 1, 2, …, 8 в результате работы описанного алгоритма получаем полиномы, которые обеспечивают оптимальную (по минимаксной норме) аппроксимацию функции exp( x ) на интервале [0, 1]. Ошибка аппроксимации в зависимости от степени полинома указана в табл. Зависимость ошибки аппроксимации от степени полинома в графической форме показана на рис. 3.

Табл. Ошибка аппроксимации функции exp( x ) на интервале [0, 1] многочленами степени n , оптимальными по минимаксной норме с весом q ( x ) = 1

n	1	2	3	4	5	6	7	8
ε	0.1	8 ⋅ 10 –3	5 ⋅ 10 –4	3 ⋅ 10 –5	10 –6	4 ⋅ 10 –8	10 –9	3 ⋅ 10 –11

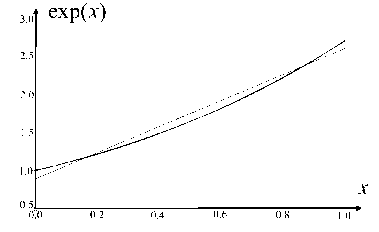
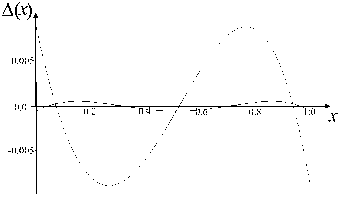
Рис. 3. Аппроксимация функции exp( x ) на отрезке [0, 1] минимаксными многочленами степени n.

а — экспоненциальная функция и ее аппроксимации, б — разность между экспоненциальной функцией и ее аппроксимациями, в — минимаксная ошибка в логарифмическом масштабе

б

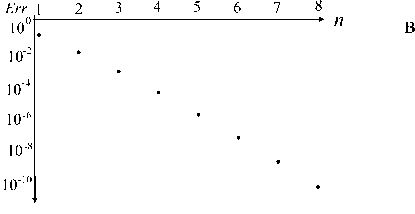
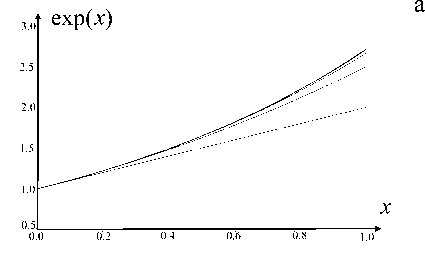
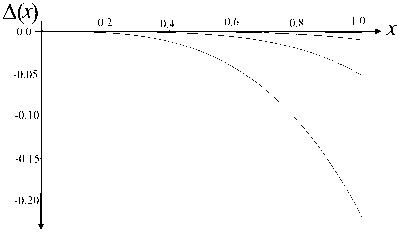
Рис. 4. Аппроксимация функции exp( x ) на интервале [0, 1] усеченными рядами Тейлора степени n.

а — экспоненциальная функция и ее аппроксимации, б — разность между экспоненциальной функцией и ее аппроксимациями, в — минимаксная ошибка в логарифмическом масштабе

б

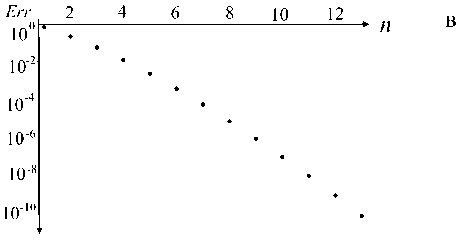
Для сравнения те же данные для усеченных рядов Тейлора показаны на рис. 4. Следует отметить, что ряд Тейлора для функции exp( x ) сходится очень быстро (в отличие от ряда Тейлора для функции log( x ), например), однако даже в этом случае минимаксное приближение дает существенное преимущество.

Работа выполнена в Институте аналитического приборостроения Российской академии наук (Санкт-Петербург) в рамках темы FFZM-2022-0009 (номер гос. регистрации 122040600002-3) государственного задания Министерства науки и высшего образования Российской Федерации № 075-01157-23-00 от 29.12.2022.

При проведении вычислений использовалась лицен-зионно чистая программа Wolfram Mathematica версии 11 (Home Edition) [23], лицензированная одному из авторов.