Численный анализ динамической прочности композитных цилиндрических оболочек при многократных импульсных воздействиях

PNRPU MECHANICS BULLETIN

Композитные материалы благодаря высокой удельной прочности находят все более широкое применение при создании различных конструкций, испытывающих интенсивные динамические нагрузки. В частности, к таким конструкциям относятся взрывозащитные камеры, для которых требуется с высокой степенью надёжности исключить их разрушение в условиях многократного воздействия импульсной нагрузки. Экспериментально установлено [1], что динамическая прочность и деформируемость стеклопластиковых цилиндрических оболочек существенно зависят от уровня импульсной нагрузки и числа нагружений. Кроме того, при повторном нагружении наблюдалось снижение величины предельной деформации оболочки [2]. Данные эффекты, связанные с неоднократным нагружением, изучались экспериментально при нагрузках, близких к предельным, что приводило к значительным повреждениям после первого нагружения и полному разрушению всего слоистого пакета при последующих нагружениях. Для обоснованного применения стеклопластиков при проектировании взрывозащитных контейнеров необходимо провести исследование их усталостной прочности при многократных импульсных воздействиях, которые существенно меньше их предельных значений. Некоторые аспекты экспериментального изучения малоцикловой усталостной прочности стеклопластиков рассматрива- лись в [3]. Обзор критериев прогрессирующего разрушения многослойных композитов содержится в работе [4]. Различные варианты моделей прогрессирующего разрушения слоистых композитов рассматривались в работах [5-15].

Предлагаемая работа посвящена численному моделированию прогрессирующего разрушения стеклопластиковых цилиндрических оболочек при многократном взрывном нагружении.

1. Постановка и метод решения задачи

Рассматривается стеклопластиковая цилиндрическая оболочка, изготовленная перекрестной намоткой лент однонаправленного композитного материала. Отнесем оболочку к ортогональной криволинейной системе координат а i ( i = 1,3), совпадающей с линиями главных кривизн и внешней нормалью к внутренней поверхности оболочки.

Коэффициенты Ламе и главные кривизны: Hj = zj = 1, H2 = z2 = 1 + k2а3, H3 = 1, k = 0, k = —, где R - радиус внутренней поверхности оболочки.

R

Кинематическая модель деформирования многослойного пакета базируется на прикладной геометрически нелинейной теории оболочек [16], в рамках которой распределение перемещений по толщине оболочки запишется в виде

U j ( а 1 , а ₂, а ₃, t ) = u j ( а 1 , а ₂, t ) + а ₃ ф j ( а 1 , а ₂, t ), ( j = 1,2), U ₃( а 1 , а ₂, а ₃, t ) = и ₃( а 1 , а ₂, t ),

где ui (а1, а2, t) - перемещения точек внутренней поверхности в направлениях осей ai(i = 1,3); фj(j = 1,2) - углы поворота нормали к внутренней поверхности.

Компоненты нелинейного тензора деформаций прикладной теории цилиндрических оболочек можно представить в виде [17]

eW =    ( ⁸ 11 ^{+ 8} 13 ^{/2 + а} 3 ^Х 11 ),      ⁽¹ ^ ²⁾ ,

^Z 1

e 12 = ^[^ 12 ^{+ 8} 13 ⁸ 23 ^{/2 + а} 3 % 12 ^]+     [ ⁸ 21 ^{+ 8} 13 ⁸ 23 ^{/2 + а} 3 % 21 ^] , ⁽¹ ^ ²⁾ ,           ⁽²⁾

^Z 1                                   z 2

^e 13 = —^(ф 1 ^+£ 13 )    П ^ ²⁾ ,

^Z 1

где дU1

£ц =+ k 1 и3      (1 ^^ 2), dat

Х„ =1^ (1 « 2), да ₁

8 ,2 =d^UL   (1 ^ 2),                                  (3)

да ₁

z„ =-|b   (1 « 2), да j

£ ₁₃ = —- - k 1 u 1     (1 о- 2).

da 1

Символ (1 ^ 2) здесь и далее обозначает, что из записанного соотношения можно получить еще одно одновременной заменой 1 на 2, 2 на 1.

Физические соотношения элементарного слоя с учетом гипотез прикладной теории оболочек запишутся в виде

(     Al )    (     А.,аЛ

^ 11 = A ii —     e ii + A 12 — -^ e 22       (1 ^ 2),

V     -33 J     V       -33 J on = Аббe12         (1 ^ 2),                               (4)

^O 13

— А в

²¹44 ^e 13 ,

^O 23    A 55 e 23

где A mn - ступенчато изменяющиеся функции переменной a ₃, которые вычисляются через модули упругости E j и коэффициенты Пуассона v ij элементарного слоя композитного материала.

В процессе нестационарного деформирования допускается локальное разрушение элементарных слоев в пакете многослойного композита. В результате разрушения отдельных элементарных слоев композита происходит перераспределение напряжений между слоями, а многослойный пакет продолжает оказывать сопротивление дальнейшему деформированию. Процесс прогрессирующего разрушения оболочки описывается в рамках модели деградации жесткостных характеристик элементарных слоев многослойного пакета, которая базируется на критерии Хоффмана [18] для композитного материала:

f   ^C1 ^(о 22 ^О 33 ) ^{+ C} 2 ^(о 33   ° 11 ) ^{+ C} 3 ^(о 11   ^О 22 ) ⁺

⁺ С 4 ° 33

⁺ С 5 О 22 ⁺ C 6 ^О 11 ⁺ C 7 ^О 23 ^{+ C} 8 ^О 13 ⁺ C 9 ^О 12

= 1,

1 1            1            1

—--1----

О 17P KC КP I7C P^p T7C ² V F 33 F 33    F 22 F 22    F 11 F 11 J

1 ( 1            1            1

—--1----

3 Z7 ^P PC   ^pP PC  рР PC

² V F 33 F 33    F 11 F 11    F 22 F 22 J

= JL C = 1

PC , 5 P

33      3322

C ^{6    р}Р  рС , C ⁷ р 2 ,

11       1123

C 8    р, , C ⁹    р^

F 13         F 12

и на критерии максимальных напряжений для волокон 011 > F1pB, 1^111 > F1CВ, вычисленных в осях ортотропии элементарного слоя. Здесь FiiP,FiiC,Fij ,F11PВ,F1C1В – пределы прочности однонаправленного композитного материала и волокон при растяжении и сжатии. В процессе деформирования и трещинообразования связующего предполагается жесткое сцепление между соседними слоями.

В зависимости от знака объемной деформации и моды разрушения композитного материала и волокон модули упругости монослоя с трещинами принимают одно из возможных значений, приведенных в таблице.

Схема редуцирования модулей упругости слоя Reduction scheme of layer elasticity moduli

G '. = ij

Характер разрушения Условия на значение объемной деформации E11 E22 E33 G12 G13 G23 ^11 > F1P 0 0 0 0 0 0 IO11I > ГЦВ e11 + e22 + e33 > 0 0 0 0 0 0 0 e11 + e22 + e33 < 0 0 E11 E202 E303 0 0 0 f (^j,Fj,Fj,Fj )> 1 e11 + e22 + e33 > 0 0 E11 E22 E33 G12 G13 G23 e11 + e22 + e33 < 0 0 E11 E202 E303 G12 G13 G23 Здесь E22, E33, Gj - значения модулей упругости и сд материала оболочки, вычисляемые по формулам [19] E22 = - вига в результате —1 max     2 e 22 , v12      pi = P       0 , 33 F22   E11 деградации -1 max 2 e33 , v13 P0 33        11 e..

ij

F.

ij

- i

E101 , E202 , E303 – значения модулей упругости в начальном неповрежденном состоянии; v12, v13 - коэффициенты Пуассона; eij - текущие значения деформаций max max

(i, j = 1,3); e22 , e33 - максимальные значения деформаций при растяжении за предыс- торию деформирования.

Процесс накопления поврежденности в материале оболочки, обусловленный многократным приложением импульсной нагрузки, учитывается посредством вычислительной схемы, в которой расчет текущего напряженно-деформированного состояния осуществляется с жесткостными характеристиками, полученными в рамках модели их деградации при предыдущем нагружении.

Будем считать, что исчерпание несущей способности оболочки происходит в момент обнуления в каком-либо поперечном сечении всех жесткостных характеристик.

Энергетически согласованная система уравнений движения прикладной теории оболочек выводится из условия стационарности функционала полной энергии оболочки. Вариационное уравнение движения цилиндрической оболочки со свободными торцами, нагруженной импульсом внутреннего давления, запишется в виде где

JJ N11

S _

+ n* £<М 13 За

д(5 u1) да1

. W + n W + гфф

21                  22                  12

да ₂          да ₂          да 1

+ n * ⁸JM + n* 5 _{И з} + M ^ 23                     22 2 3        11

va 2                                      (-/^^1

+ Mn /j52 ’ + m fM

22                   12

да 2          да1

+ M 21

*

- ^N 23 К 2 ⁵ u 2 +

^ + еи5Ф1 + да 2

+ Q235ф2 dа1 dа2 + JJ[(B^ + B 2ф3 )5 u + J

+ ( B 11 U₂ + B 2 2 ₂ ) 5 u ₂ + B 11 u₃ 5 u ₃ + ( B 22 2 1 + B ₂₁ u 1 ) 5ф 1 + + ( B 22 2 ₂ + B ₂₁ U₂ ) 5ф ₂ J d а 1 d а ₂ - Jj P₃ 5 u ₃ d а 1 d а ₂ = 0,

N 3 = Q 13 + N _nS 13 + N 12 8 23 , (1 ^ 2).

B_n = p ( h + k ₂ h ²/2 ) ;     B ₂₂ = p ( h³/3 + k ₂ h 4 /4 ) ;    B ₁₂

^N 11    ^B 11 ⁸ 11 ^{+ B} 12 ⁸ 22 ⁺ C 11 X 11 ⁺ C 12 ^X 22

N =B "s +S¹²8 +C¹¹y +C¹²y

^1N 12    '^u33 ⁸ 12 ^{+ 2}-^,33 ⁸ 21 ⁺ ^33 Л 12 ⁺ '-'33 ^X 21

= ^C 11 ⁸ 11 ^{+ C}12 ⁸ 22 ^{+ D}1’ ^X 11 ^{+ D} 12 ^X 22

= C H8 + C128 +D11y + Z)12'y

33 ^ 12 + v-33 ^ 21 + ^33 X 12 ⁺ -^33 Л 21

Q 13 = K 1 ( 8 13 +Ф 1 ) (1 ^ 2),

= B ₂₁ = p ( h ²/2+ k ₂ h ³/3 ) ,

(1 о 2),

(1 о 2),

(1 ^ 2),

(1 ^ 2),

⁸ 11 ⁺⁸ 13^/2 ;       ⁸ 12 ⁸ 12 ⁺⁸ 13 ⁸ 23^/2

(1 ^ 2).

В = 1 ⁽⁰⁾,

JJ JJ ,

JJ(0)

33     ^33, JJ ,

D = I(2)

JJ       JJ,

B 12    B 21    J 12 ’

12       21       (0)

33      33      33

(2) ^12   ^21   ^12 ’

C = 1(1), JJ JJ ’ cJJ = T^

’     C 33     I 33, JJ ’

D^jj = I ⁽²⁾

33    ¹33, JJ

C, =C = J,(1)

12    ^21    ^12 ’

12        21        (1)

C 33 = C 33 = J 33 ,

D ¹² -D²¹ = J⁽²⁾

33       33 33 ,

h = z

^z к - 1 ’

h =(z

z .J/2,

J h ² Z

K h ⁽" ) h

1 -1

( 1 + h к k )

к = 1

Д ^{(kk )} AJ + 3 J + 3

K

(1 о 2) ( J = 1,2),

K

—У A(1K)h KЧ i +1 Z 11 2 (

k = 1

z k⁺¹

- z k - 1 ) , ( i = 0,1,2 ) (1 о 2),

K

- z k - 1 )   (1 о 2),

'( i )                     j( к)_Н( к)/ /+1

33,11 = . 1 Z A11 H 2 (zк i + 1 к=1

K

12¹ = -^ Z A l l ) (-- к⁺¹ i ⁺ 1 к = 1

- Z i ⁺¹ ) z к - 1 ,

K

J33 = —7 Z A331(zK+l-zк *-’1) (i = 0,1,2), i + 1 к=1

где P ₃ - нагрузка по направлению координатной оси a ₃; S - область интегрирования на внутренней поверхности оболочки; A J ) - эффективные жесткостные характеристики слоя, которые вычисляются через модули упругости и коэффициенты Пуассона [16]; z _к -координаты слоев, отсчитываемые от внутренней поверхности оболочки.

Минимизация функционала полной энергии оболочки (5) позволяет получить систему уравнений движения

L ( N ) = B„U ’ + B_V1„ L 2 ( N ) + n ; ₃ k 2 = B „ u + B _l2 i p ₂ ’

L1( m )-q, = B22ip1 + B21 u„ L2 ( m )-e2i = B,,ф2+B21a2, l_ ( t )=®2l+5Z21 da1 da2

ZNH + ZN23 - k N + F = b u

2 22 3       11 .

da ’    da ₂

и естественные граничные условия

N _n = 0, N₁₂ = 0, N * = 0, M 11 = 0, M ₁₂ = 0 (1 ^ 2).

Дополняя соотношения (6), (7) необходимым числом начальных условий и\ а. 1 , а 2 ,0) = u₁ °( a 1 , a 2 ),     ф i (a^ a 2 ,0) = ф X a 2 ),

U i ( a 1 , a ₂,0) = U i Xa 2 ),     ф i ( a_pa 2 ,0) = ф ⁰ ( a 1 , a ₂), ( i = 1,3; j = 1,2),

получим полную систему уравнений для анализа нелинейных волновых процессов деформации и послойного разрушения цилиндрических оболочек, полученных перекрестной намоткой однонаправленного композитного материала.

Численный метод решения сформулированной задачи основывается на явной вариационно-разностной схеме [20].

• 2.    Результаты исследования

  Рассматривалась оболочка радиусом внутренней поверхности R = 0,15 м, толщиной h = 0,00819 м и длиной L = 4 R , выполненная из стеклопластика со следующими жестко-стными и прочностными характеристиками элементарного слоя и волокон[21]: E 11 = 55,0 ГПа, E ₂₂ = E ₃₃ = 9,04 ГПа, v₁₂ = v₁₃ = 0,276, v₂₃ = 0,3, G₁₂ = G ₁₃ = 5,08 ГПа, G ₂₃ = 5,2 ГПа, p = 2010 кг/м³, FC = 1,5 ГПа, F C = 0,397 ГПа, F P = F ₃ P = 0,0267 ГПа, F C = F ₃ C = 0,0719 ГПа, F , = F ₃ = 0,0357 ГПа, F ₂₃ = 0,04 ГПа, F ™ = 2,8 ГПа, F C^В = 0,7425 ГПа.

В расчетах импульс внутреннего давления задавался с помощью эмпирической зависимости

0,35 mqjl ³ при t <  0,35 l / y q ,

при t >  0,35 l / Cq ,

где m - масса заряда; q = 4,77-10 6 Дж/кг - теплотворная способность взрывчатого вещества (ВВ); l - расстояние от центра заряда до точки внутренней поверхности оболочки.

Достоверность рассматриваемого подхода подтверждалась сравнением численных расчетов с экспериментальными данными [2] по значениям максимальных кольцевых деформаций e ₂₂ в центральном сечении неразрушившейся оболочки и периоду радиальных колебаний T , полученным для оболочки со структурой пакета | 90⁰ ^ 16 при нагружении однократным зарядом ВВ массой m = 0,0206 кг. В эксперименте e *₂ = 0,4% , T -10⁶ = 180 с, в расчете e ₂₂ = 0,3% , T -10⁶ = 190 с.Наблюдается достаточно хорошее совпадение результатов как по амплитуде, так и периоду колебаний.

Далее рассматривалась задача динамической прочности стеклопластиковой цилиндрической оболочки толщиной h = 0,0102 м со структурой армирования |± 45⁰, 90⁰ ₂ J 4 при многократных импульсных воздействиях, которые существенно меньше их предельных значений.

Типичные зависимости радиальных колебаний в центральном сечении оболочки показаны на рис. 1 для пяти последовательных нагружений зарядом ВВ массой m = 0,105 кг.

Видно, что с ростом числа нагружений наблюдается увеличение амплитуды и периода колебаний, обусловленное снижением жесткостных характеристик многослойного пакета вследствие разрушения некоторых элементарных слоев.

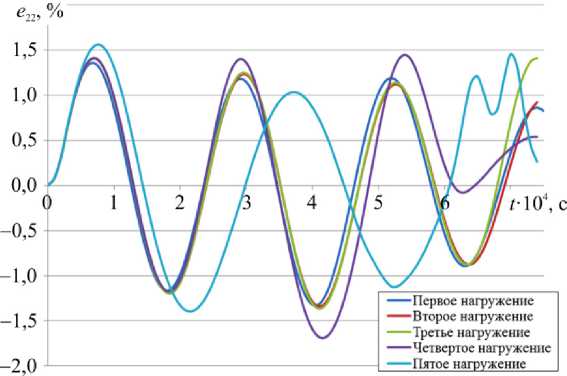
Рис. 1. Осциллограммы окружных деформаций в центральном сечении при многократном нагружении Fig. 1. Waveform circumferential deformations in the central section with repeated loading

Иллюстрация процесса разрушения оболочки при многократном нагружении зарядом ВВ массой m = 0,105 кг представлена на рис. 2–4. На рис. 2 для двух моментов времени показаны деформированные конфигурации оболочки с нанесенными зонами разрушения внешнего слоя.

t = 1,0⋅10–4 с t = 7,0⋅10–4 с       t = 1,0⋅10–4 с    t = 7,0⋅10–4 с       t = 1,0⋅10–4 с    t = 7,0⋅10–4 с а                               б                              в

Рис. 2. Деформированные конфигурации оболочки (прогибы увеличены в пять раз): а – первое нагружение; б – четвертое нагружение; в – пятое нагружение

Fig. 2. The deformed configuration of the shell (deflections magnified five times): a – first loading; b – loading the fourth; с – fifth loading

На рис. 3 показана соответствующая кинетика развития зон разрушения по толщине пакета слоев в центральном сечении оболочки для пяти последовательных нагружений.

Здесь светлый фон соответствует зонам, в которых разрушения отсутствуют; серый фон – зоны разрушения матрицы; в зонах черного фона происходит разрушение волокон. Процесс разрушения стеклопластиковых оболочек при многократных импульсных воздействиях аналогичен ранее полученным результатам при однократном нагружении [22], что свидетельствует о слабом влиянии скорости деформации на характер возникающих в композите повреждений.

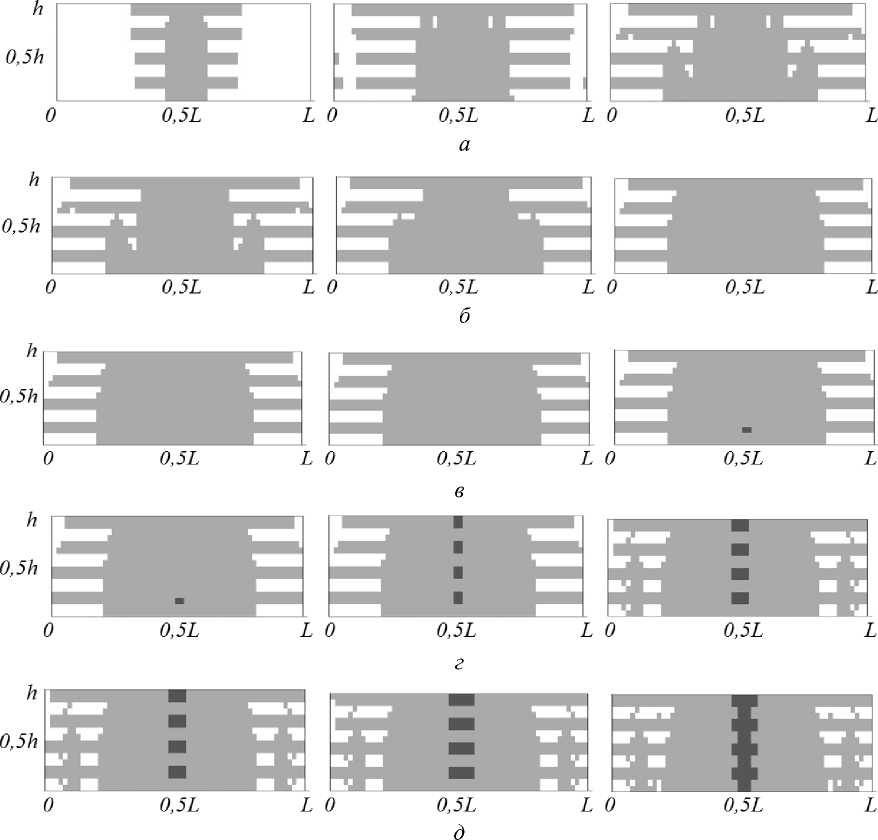
t = 1,0 ⋅ 10^–4 с                       t = 4,0 ⋅ 10^–4 с                      t = 7,0 ⋅ 10^–4 с

Рис. 3. Кинетика зон разрушения по толщине оболочки: а – первое нагружение;

б – второе нагружение; в – третье нагружение; г – четвертое нагружение; д – пятое нагружение Fig. 3. Kinetics of fracture zones across the shell thickness: a – first loading; b – second loading;

с – loading the third; d – fourth loading; е – the fifth loading

На рис. 4 показаны экспериментальные [3] и расчетные зависимости предельных значений окружных деформаций e ₂ ^* ₂ от логарифма числа нагружений N .

Анализ полученных результатов показал, что для данного типа стеклопластиковых оболочек кольцевая деформация линейно зависит от логарифма числа нагружений до разрушения. Разброс расчетных данных для e ₂ ^* ₂ при lg N = 0 объясняется тем, что результаты получены для различных масс ВВ, при которых разрушение происходило при однократном нагружении. Кроме того, существует граничный уровень предельной нагрузки, при котором разрушение не наблюдается, а число нагружений может быть достаточно большим. Отмеченный эффект может быть связан с тем, что рассматриваемая модель не учитывает накопление повреждений в материале при нагрузках меньше критических. При этом уровень максимальных кольцевых деформаций ниже

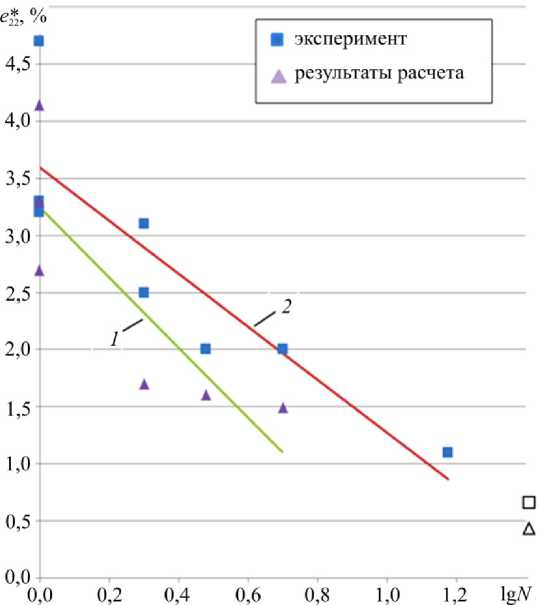
Рис. 4. Максимальные окружные деформации в зависимости от числа нагружений:

– разрушение; □ A – нет разрушения; 1 – эксперимент; 2 – расчет

Fig. 4. The maximum circumferential strain depending on the number of loadings:

■ A – destruction; □ A – no destruction; 1 – experiment; 2 – calculation их предельных значений по сравнению с однократным нагружением примерно в де-сятьраз. Полученные результаты удовлетворительно коррелируют с экспериментальными данными [3].

Заключение

Предложенная расчетная модель позволяет с удовлетворительной точностью описывать процесс послойного прогрессирующего разрушения стеклопластиковых цилиндрических оболочек при многократных импульсных воздействиях. Значения предельных окружных деформаций при многократном импульсном нагружении примерно на порядок меньше по сравнению с соответствующими предельными значениями при однократном нагружении, что удовлетворительно согласуется с результатами экспериментальных испытаний.

Работа выполнена при частичном финансировании в рамках базовой части государственного задания Минобрнауки (проект № 2014/134 2226) и грантов РФФИ(проекты № 15-08-04268, № 16-08-01124), разработка расчетной модели выполнена за счет средств РНФ (проект №16-19-10237).