Численный анализ динамики газового потока пиролиза пропана

Введение. Исследуется процесс пиролиза пропана в проточном реакторе в режиме подачи энергии через постоянный внешний нагрев. Для комплексного исследования процесса во всевозможных условиях и для обеспечения перехода от лабораторных установок к промышленным необходимо провести численный анализ результатов моделирования течения газа в реакторе с учётом химических процессов. В работе представлены результаты численного моделирования трехмерной динамики газового потока пиролиза пропана в реакторе в программном пакете ANSYS Fluent с использованием компактной кинетической модели.

Материалы и методы. Авторами предложена новая компактная кинетическая схема пиролиза пропана, которая была получена на основе методов локального и глобального анализа чувствительности модели. Представлена математическая модель, используемая в пакете ANSYS Fluent, которая представляет собой уравнения неразрывности, сохранения импульса, сохранения энергии, дополненные уравнениями неразрывности для каждой компоненты газа.

Результаты исследования . Впервые проведено численное моделирование трехмерной динамики газового потока пиролиза пропана в реакторе в программном пакете ANSYS Fluent с использованием компактной кинетической модели. Проведены расчеты динамики газового потока пиролиза пропана в лабораторном реакторе с учетом процессов диффузии, химических реакций и их тепловых эффектов. Результаты численных расчетов и экспериментальные исследования по конверсии пропана хорошо согласуются между собой.

Обсуждение и заключения . Результаты исследования и моделирования пиролиза пропана могут составить основу для описания процесса в объеме реактора под воздействием лазерного излучения.

Introduction. Homogeneous pyrolysis of propane is studied in a flow reactor with constant external heating. A numerical analysis of the results of simulating the gas flow in the reactor with account of chemical processes is required for a comprehensive study of the process under all kinds of conditions and for the control of the transition from laboratory facilities to the industrial ones. The results of the numerical modeling of the three-dimensional gas flow dynamics of propane pyrolysis in the reactor based on the ANSYS Fluent using a compact kinetic model are presented.

Materials and Methods. An acceptable size kinetic scheme of the pyrolysis of propane is proposed by the authors. The scheme is obtained using the methods of local and global sensitivity analysis of the model. The mathematical model used in the ANSYS Fluent package is given. The model is the equation of continuity, conservation of momentum, and conservation of energy, supplemented by the continuity equations for each gas component.

Research Results. The numerical simulation of the threedimensional dynamics of the gas flow of propane pyrolysis using the ANSYS Fluent software package and a compact kinetic model is carried out for the first time. Calculations of the gas flow dynamics of propane pyrolysis are conducted in the laboratory reactor with account of the diffusion processes, chemical reactions and their thermal effects. The numerical calculations results correlate well with the experimental studies on the conversion of propane.

Discussion and Conclusions. The results of the research and simulation of the propane pyrolysis can form the basis for describing the process in the reactor volume under the influence of the laser radiation.

Информатика, вычислительная техника и управление

Образец для цитирования: Губайдуллин, И. М. Числен-      For citation: I.M. Gubaydullin, L.F. Nurislamova. Numerical ный анализ динамики газового потока пиролиза пропана / analysis of gas flow dynamics of propane pyrolysis. Vestnik of И. М. Губайдуллин, Л. Ф. Нурисламова // Вестник Дон-      DSTU, 2018, vol. 18, no.1, pp. 69-76.

ского гос.техн.ун-та — 2018. — №1. — Т. 18 — С. 69-76.

Введение. В Институте катализа им. Г.К. Борескова СО РАН с целью создания экономически эффективной технологии переработки углеводородного сырья изучают химическую реакцию пиролиза пропана в лабораторном реакторе проточного типа. Газофазные условия при протекании процесса формируются за счет внешнего нагрева стенок реактора и за счет подачи лазерного излучения, что обеспечивает дополнительную генерацию радикалов [1]. При этом происходит повышение реакционной способности смеси, и тем самым увеличивается выход полезных продуктов. Кроме того, уменьшается образование кокса и побочных продуктов реакции вследствие возможности проведения процесса пиролиза пропана при более низкой температуре.

Для комплексного исследования процесса при различных условиях и для обеспечения перехода от лабораторных установок к промышленным, необходимо провести численный анализ результатов моделирования течения газа в реакторе с учётом химических процессов. Общемировой практикой при математическом моделировании является использование мощных программных комплексов 3D-моделирования промышленных и лабораторных реакторов (например, коммерческие пакеты Fluent, FloWizard, FlowVision), которые могут эксплуатироваться на однопроцессорных и многопроцессорных ЭВМ.

При трехмерном моделировании газовой динамики в реакторе основную трудность представляет собой выбор кинетической модели реакции. Пиролиз пропана является радикально-цепной реакцией, и численное интегрирование получаемой жесткой системы дифференциальных уравнений представляет собой вычислительно затратную задачу. Для описания пиролиза пропана были установлены многочисленные кинетические модели, среди которых можно условно выделить компактные (описывают пиролиз пропана в заданных условиях с относительно небольшим числом стадий, до 20) и детализированные. Для 3D-моделирования, как правило, используют компактные схемы, что обусловлено большими временными затратами, возникающими при расчетах по детализированным схемам [2, 3].

В настоящее время в основном изучено одно- и двумерное моделирование процесса газофазного пиролиза пропана [4–6]. Для численного изучения процессов теплообмена и динамики данного процесса в трехмерном пространстве авторами был выбран пакет ANSYS Fluent (лицензия Сибирского суперкомпьютерного центра СО РАН) [7].

В настоящей статье рассматриваются результаты верификации численной модели трехмерного реагирующего газа, построенной на основе пакета ANSYS Fluent путем сравнения с экспериментальными данными, полученными для термического пиролиза пропана в проточном реакторе в режиме подачи энергии в реактор через постоянный внешний нагрев.

Кинетическая модель. Термическое разложение предельных углеводородов сопровождается разнообразными и многочисленными параллельными процессами, что приводит к образованию десятка веществ и возможности протекания сотни реакций. Количество стадий и веществ, включенных в кинетическую модель, должно быть ограничено. Это мотивируется необходимостью интегрирования кинетической модели в программный комплекс 3D-моделирования ANSYS Fluent для расчета трехмерной динамики газа. Брутто-схемы не дают удовлетворительного описания пространственного распределения по реактору протекания химических реакций с радикально-цепными механизмами. Использование детальных кинетических механизмов при моделировании процесса пиролиза пропана, включающих химические превращения, важно для полного и точного описания процессов в широком диапазоне температур. Однако их использование в трехмерных численных расчетах реакторов приводит к неприемлемым временам расчетов даже на современных суперкомпьютерах. Таким образом необходимо найти баланс между точностью модели и временем вычислений.

Рассмотрев различные кинетические схемы в пакете ANSYS, была получена схема приемлемого раз-мера(табл. 1), описывающая расход пропана и образования основных продуктов реакции [8–11]. Константы элементарных стадий широко представлены в справочной литературе, в научных статьях, а также в химических базах данных, прежде всего в NIST. В таблице 1 приведены элементарные химические стадии пиролиза пропана.

Схема пиролиза пропана

Таблица 1

Table 1

Scheme of propane pyrolysis

№	Стадия Stage	А , 1/с или л/(моль·с) А , 1/с or L/(mol·s)	Е , кДж/моль Е, kJ/mol	n
1	C 3 H 8 → C 2 H 5 • + CH 3 •	2,78e+15	376	-1,8
2	C 2 H 5 • + CH 3 •→ C 3 H 8	2,83e+10	0	-0,5
3	C 2 H 5 • → C 2 H 4 + H•	4,31e+09	155	1,19
4	C 2 H 4 + H•→ C 2 H 5 •	4,09e+09	4,15	1,49
5	C 3 H 8 +CH 3 • → CH 4 + n- C 3 H 7 •	2,98e+05	29,93	3,65
6	C 3 H 8 +CH 3 • → CH 4 + iso- C 3 H 7 •	5,48e+05	22,95	3,46
7	C 3 H 8 +H• → H 2 + n- C 3 H 7 •	2,55e+09	28,27	2,54
8	C 3 H 8 +H• → H 2 + iso- C 3 H 7 •	1,13e+09	18,71	2,4
9	n- C 3 H 7 • → C 2 H 4 + CH 3 •	1,20e+10	126	0
10	iso- C 3 H 7 • → C 3 H 6 + H•	1,60e+10	150	0
11	n- C 3 H 7 • → C 3 H 6 + H•	1,09e+10	149	0,17
12	C 3 H 6 + H•→ n- C 3 H 7 •	1,30e+10	13,64	0
13	C 3 H 8 + C 2 H 5 • → C 2 H 6 + n- C 3 H 7 •	9,70e+05	38,25	3,65
14	C 3 H 8 + C 2 H 3 • → C 2 H 4 + iso- C 3 H 7 •	4,79e+07	36,92	3,1
15	C 3 H 6 + H• → H 2 +C 3 H 5 •	2,61e+08	10,39	2,5
16	H 2 +C 3 H 5 • → C 3 H 6 + H•	8,37e+07	79,49	2,38
17	C 3 H 8 + C 3 H 5 • → C 3 H 6 + n- C 3 H 7 •	3,44e+07	83,06	3,3
18	C 2 H 4 +CH 3 • → CH 4 + C 2 H 3 •	9,45e+06	39,74	3,7
19	CH 4 + C 2 H 3 • → C 2 H 4 +CH 3 •	1,28e+07	22,86	4,02
20	H 2 +CH 3 • → CH 4 + H•	1,52e+07	36,42	3,12
21	C 2 H 4 + C 2 H 3 • → C 4 H 7 •	9,21e+08	19	0
22	C 3 H 6 + C 2 H 5 • → C 2 H 6 + C 3 H 5 •	1,02e+06	27,77	3,5
23	C 4 H 7 •→ C 4 H 6 + H•	6,40e+09	144,2	0
24	C 4 H 7 •→ C 2 H 4 + C 2 H 3 •	2,10e+10	149,2	0
25	C 2 H 6 + H• → H 2 +C 2 H 5 •	2,48e+09	35,34	1,5
26	C 3 H 5 • → C 2 H 2 + CH 3 •	3,00e+10	151	0
27	C 4 H 8 → C 3 H 5 • + CH 3 •	1,00e+13	305	0
28	CH 3 • + CH 3 • → C 2 H 6	2,64e+10	0	0
29	C 3 H 5 • + CH 3 • → C 4 H 8	1,64e+10	-0,55	-0,32
30	C 2 H 3 • + CH 3 • → C 3 H 6	9,56e+11	0,57	-0,54

Математическая модель. Математическая модель представляет собой уравнения неразрывности, сохранения импульса, сохранения энергии, дополненные уравнениями неразрывности для каждой компоненты газа:

∂ρ

+∇⋅ ( ρ v ) = 0,

∂ t

∂ ( ρ v )

+∇⋅ ( ρ v ⊗ v ) +∇ p = 0,

∂ t

Информатика, вычислительная техника и управление

d ( p E )

+v- ( v ( p e + p )) + q = s ,

St d (p Y)                _

----i- + V- ( V p Yi ) + V- Ji = Ri .

d t

Уравнение состояния смеси идеальных газов имеет вид:

p = p RT Z ( Y / M wj ) ^j

Начальные условия задают состояние рассматриваемого объекта в начальный момент времени: p ( x,t 0 ) = P o , ^v ( x,t o ) = ^(u ( x,t o ) , ^v ( Xt 0 ) , ^w ( X t 0 ) ^{) T} , p ( x,t 0 ) = P o , ^T ( x,t 0 ) = ^T 0 , Y ( x,t 0 ) = Y 0 -

Здесь p — плотность газа (кг/м3), v — скорость газа (м/с), p — давление (Па), рE — полная энергия в единице объема (Дж/м3),  hj — энтальпия (Дж/кг), cpj  — удельная теплоемкость вещества j (Дж/Кэкг), hj                                                                                                                                              3.

S h = -Z— — R — нагрев (охлаждение) в результате химической реакции и внешних воздействии (Дж/е э м ), j_M wj

N

Y i — локальная массовая доля вещества г , R i = M_wj Z R r — объемная скорость образования вещества г r = 1

(кг/е э м ³ ), J Rir — молярный коэффициент Аррениуса образования (расхода) вещества г в ходе реакции r (1/е э м ³ ) , Mwi — молекулярная масса вещества г (кг), R — универсальная газовая постоянная (Дж/моль э К), T — температура ( К ) .

Более подробно математическая модель представлена в работе [7].

Результаты исследования. Были проведены расчеты динамики газового потока пиролиза пропана с учетом процессов диффузии, тепловых эффектов реакции и тепловых процессов с включением разработанной кинетической модели. Кинетическая модель является первостепенной задачей при моделировании любого нефтехимического процесса. На ее основе получают оптимальные условия проведения нефтехимического процесса. Исследуются важные явления, например, реакционная способность участвующих в реакции всех веществ, образование и устойчивое существование индукционных (взрывных) периодов и т. д. [12, 13]. В математической модели реактора рассматривается нестационарное пространственное трехмерное течение газа; ламинарный режим течения с диффузией процессов. В модель включены уравнения сохранения массы, импульса, энергии и уравнения сохранения отдельных химических веществ. Скорость реакции рассчитывается из уравнения Аррениуса на основе кинетической модели, которая был разработана при использовании методов локального и глобального анализа чувствительности [14-17].

Температура смеси, подаваемой в реактор, составляла 600 К. Пристеночная температура задавалась в диапазоне от 820 до 990 К, температура входных и выходных трубок — 300 К. Подаваемые расходы через верхний и нижний входы — 1,758 мг/сек. Ввод защитного газа (метана) осуществлялся с расходом 0,221 мг/сек и температурой 300 К.

Результаты моделирования (профиль температуры и мольных долей основных компонентов) приведены на рисунках 1-5 для одного из моментов установления течения в реакторе, когда распределение температуры и скорости потока реагентов на выходе реактора меняются незначительно.

Защитный газ (метан) ограничивает область реакционной зоны и предохраняет от перегрева торцевые стенки с окнами для излучения. Метан преимущественно остается в буферных зонах, и лишь малая его часть проникает в реакционную зону. Потоки холодного газа, поступающего через вводы исходной смеси, не успевают охладить двигающуюся по реакционной зоне смесь. Температура газа в реакционной зоне меняется от высоких пристеночных значений до минимума в центре. Такое распределение способствует потоку энергии от стенок к оси реактора. Химическая реакция протекает почти по всему объему реакционной зоны с более активным превращением в пристеночной разогретой области. Появление пропана и продуктов реакции в правой и левой «защитных» областях реактора объясняется диффузией газа. Большая массовая доля продуктов реакции в правой части реакционной зоны объясняется тем, что в продолжающем движение газе реакции не прекращаются. Превращение пропана проходит во всей реакционной зоне.

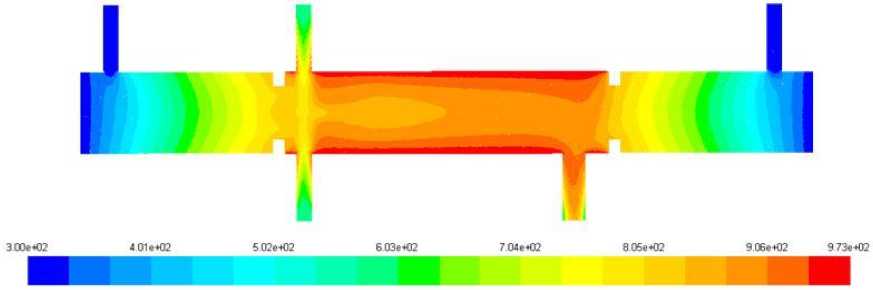
Рис. 1. Распределение температуры (К) в реакторе в продольном сечении

Fig. 1. Temperature distribution (К) at longitudinal section in reactor

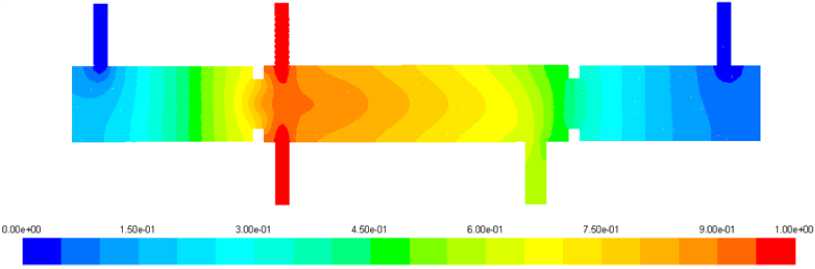
Рис. 2. Распределение в продольном сечении мольных долей пропана

Fig. 2. Propane mole fraction distribution at longitudinal section

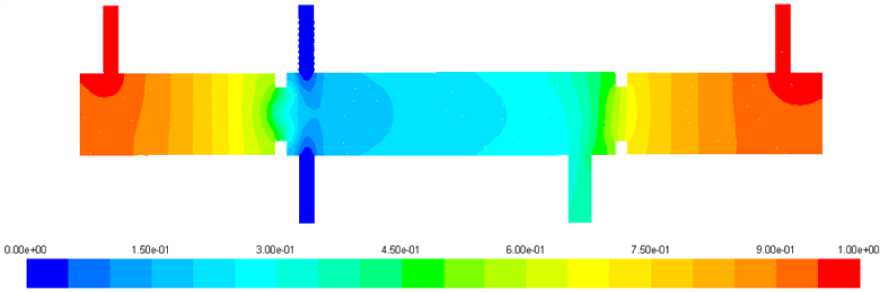
Рис. 3. Распределение в продольном сечении мольных долей метана

Fig. 3. Methane mole fraction distribution at longitudinal section

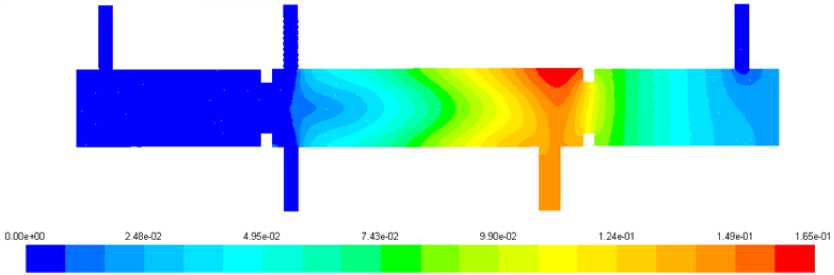
Рис. 4. Распределение в продольном сечении мольных долей этилена

Информатика, вычислительная техника и управление

Fig. 4. Ethylene mole fraction distribution at longitudinal section

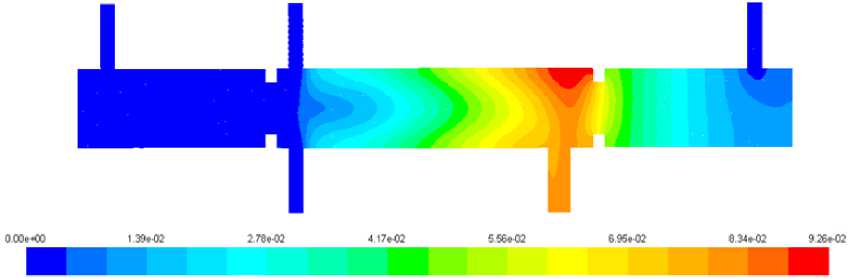
Рис. 5. Распределение в продольном сечении мольных долей водорода

Fig. 5. Hydrogen mole fraction distribution at longitudinal section

Для верификации трехмерной модели использовалось сопоставление экспериментальных и расчетных данных по зависимости конверсии пропана от пристеночной температуры. Конверсия пропана при таком распределении температуры и с приведенной выше схемой близка к экспериментальным значениям (табл. 2).

Таблица 2

Table 2

Сравнение расчетных и экспериментальных данных по конверсии пропана

Comparison of calculated and experimental data on propane conversion

Tемпература, K Temperature, K	899	923	948	973
Эксперимент, % Experiment, %	7,3	12,7	22	36
Расчет, % Calculation, %	6,8	15,6	27,7	37,1

Заключение. В программном пакете ANSYS Fluent проведены расчеты динамики газового потока пиролиза пропана в лабораторном реакторе с учетом процессов диффузии и тепловых эффектов реакции в программном пакете ANSYS Fluent с включением разработанной компактной схемы реакции. Проведен вычислительный эксперимент и найдены зависимости выхода продуктов реакции и расхода подаваемой смеси по длине реакционной зоны. Результаты численных расчетов и экспериментальные исследования по конверсии пропана хорошо согласуются между собой. Успешные результаты моделирования неизотермического химического реактора с ламинарным потоком реагентов открывают возможность использования этого типа реакторов для изучения процесса в объеме реактора под воздействием лазерного излучения.