Численный анализ функциональных свойств 3D-резонатора плазмонного нанолазера с учетом нелокальности и наличия призмы методом дискретных источников

Наноплазмонные устройства позволяют получать сверхвысокую концентрацию электромагнитного поля в областях, размеры которых на порядки превышают рэлеевский предел оптического оборудования [1–2]. Это обстоятельство даёт возможность использовать плазмонный резонанс в многочисленных практических приложениях, таких как биосенсоры, солнечные элементы, суперлинзы, Рамановская спектроскопия, плазмонные нанолазеры (ПН) и многие другие [3–7]. Совершенствование схем ПН является одной из фундаментальных задач квантовой наноплаз-моники. Идея состоит в том, чтобы использовать плазмонный резонанс вместо фотонных схем. Плазмонные нанолазеры, основанные на использовании слоистых 3D-резонаторов, имеют преимущества наноразмера, низкого энергетического порога и супермалого времени отклика [7–8].

Первыми, кто предложил концепцию лазерного резонатора, основанного на поверхностных плазмонах, взаимодействующих с усиливающей средой, были Сударкин и Демкович [9]. Позднее, в 2003 году, Бергманом и Штокманом [10] был предложен сам термин SPASER (Surface Plasmon Amplificationby Stimulated Emissionof Radiation) и создана теория генерации спазеров с использованием локализованных плазмонов. Сходная концепция обсуждалась в работе

Проценко [11]. Первая демонстрация ПН была реализована Ногиновым и соавторами [12]. Группа Ноги-нова в действующем прототипе спазера использовала в качестве резонатора одиночную золотую наночастицу сферической формы диаметром 14 нм, заключенную в кварцевую оболочку и расположенную на поверхности стеклянной призмы. Позже похожая экспериментальная реализация спазера демонстрировалась группой Плеханова [13]. Больше деталей по теме плазмонного нанолазера можно найти в недавнем обзоре [14].

Как уже отмечалось, ключевым элементом 3D-резонатора ПН является плазмонная наночастица, для описания резонансных свойств которой используется классическая теория Максвелла [15]. Однако непрерывная миниатюризация плазмонных элементов приводит к тому, что классической системы уравнений Максвелла оказывается недостаточно для достоверного описания функционирования схем наноплаз-монных устройств, так как внутри плазмонного материала возникает квантовый эффект нелокальности (ЭН), который существенно меняет оптические характеристики [16]. Анализ влияния ЭН приводит к необходимости учета возникающих продольных полей и дополнительного граничного условия на поверхностях слоев. Для описания ЭН на основе гидродинамической теории была разработана квазикласси-ческая теория Максвелла, учитывающая наличие продольных электромагнитных волн и дополнительных граничных условий. В данной работе мы будем ориентироваться на теорию обобщенного нелокального отклика (ОНО) [17], которая представляет собой развитие гидродинамической теории с возможностью проводить анализ оптических характеристик произвольных рассеивателей, включая слоистые.

Мы используем модель ОНО в рамках метода дискретных источников (МДИ) [18]. Этот метод представляет собой универсальную компьютерную технологию построения вычислительных алгоритмов для широкого круга задач квантовой наноплазмони-ки. МДИ – строгий численно аналитический поверхностно ориентированный метод. Он основан на представлении полей (включая продольные поля внутри металлической оболочки) в виде конечной линейной комбинации распределенных мультиполей низшего порядка [19], удовлетворяющих полуклассическим уравнениям Максвелла. Для представления рассеянных полей вне частицы используется тензор Грина полупространства [20]. Таким образом, представления полей во всех областях удовлетворяют уравнениям Максвелла, условиям на бесконечности и условиям сопряжения на бесконечной поверхности призмы. Соответствующие амплитуды ДИ определяются из условий сопряжения, поставленных на поверхностях слоистой частицы с учётом дополнительных граничных условий. Отличительная особенность МДИ состоит в том, что он позволяет оценить реальную погрешность полученного решения посредством вычисления невязки полей на поверхностях слоев частицы. Данное обстоятельство дает возможность вычислять ближние поля с гарантированной точностью, что особенно существенно при анализе усиления интенсивности вблизи частицы или сечения поглощения. Все эти преимущества уже позволили использовать МДИ для анализа плазмонных наноструктур с учетом ЭН в рамках модели обобщенного нелокального отклика [21 – 23]. В [24] предложена модель анализа оптических характеристик слоистых частиц, расположенных на подложке, с учетом ОНО. Было показано, что диэлектрическая частица с плазмонным покрытием реализует большее усиление поля по сравнению с металлической с диэлектрическим покрытием. В данной работе компьютерная реализация этой модели используется для детального анализа функциональных свойств слоистого резонатора ПН.

Постановка задачи дифракции

Будем рассматривать пространство R ³, разделенное на два полупространства: верхнее – D 0 :( z >0) и диэлектрическая призма – D 1 :( z <0). Обозначим границу раздела X :( z = 0). Пусть сферическая слоистая частица целиком располагается в верхнем полупространстве D 0 . Ядро частицы обозначим как D i , а металлическую оболочку – как D s . Соответствующие границы ядра и оболочки будем обозначать как 5 D i , $

(рис. 1). Все среды предполагаются немагнитными, а их диэлектрические проницаемости обозначим s v , v = 0,1, i , $ .

Одним из проявлений ЭН является возникновение внутри металла продольных электромагнитных полей. В этом случае электрическое поле Е перестает быть чисто поперечным ( div E ^T =0) за счет формирования объемного заряда, и для адекватного описания процессов возникает необходимость привлечения продольных полей ( rot E ^L =0 ) [16]. Для учета нело-кальности используется гидродинамическая теория Друдэ и ее обобщение – модель ОНО [17]. В рамках теории ОНО проводится обобщение закона Ома для тока проводимости внутри металла , то есть осуществляется переход следующего вида

J = a E ^ ^ 2 V ( V- J ) + J a E ,              (1)

где a - проводимость металла, а ^ - параметр нело-кальности [17]. В результате изменяется соответствующее уравнение системы Максвелла для магнитного поля. Итак, внутри металлической оболочки электрическое поле представляется как сумма поперечного и продольного полей E $ = E T + E L , div E T = 0, rot E L = 0 . Можно показать, что каждое из этих полей внутри оболочки D s удовлетворяет уравнениям Гельмгольца

A E T ( M ) + k T E $ ( M ) = 0, k T = k 2 s $ , M e D $ ,    (2)

A E L ( M ) + k L E L ( M ) = 0, k L =s $ / ^ .             (3)

Здесь k T , k L – поперечное и продольное волновые числа, а k = to / c .

Перейдем к формулировке математической постановки граничной задачи рассеяния для системы уравнений Максвелла с учетом ЭН. Обозначим {E0, H0} поле внешнего возбуждения – плоскую электромагнитную волну линейной поляризацию. Тогда постановка граничной задачи рассеяния с учетом ЭН может быть записана в следующем виде rot Hv = jksvEv, rot Ev = - jkHv в Dv, v = 0,1, i, rot H$ = jk (s$ +^2VV) E$ (M), rot E$ =-jkH$ в D$, п,х(к,(P)- E$ (P)) = 0, n,x(Hi (P)- H$ (P)) = 0, sin ■ Ei (P) = sLni ■ E$ (P), P e dDi, ez x(E0(Q) - Ei(Q) ) = 0, ez x(Ha(Q) - Hi(Q) ) = 0, Q eX,                 (4)

n$ x(E$ (P)- E0 (P)) = n$ x E0 (P), n$ x(H$ (P)- H0 (P)) = n$ x H0 (P), sLn$ ■ E$ (P) =S0n$ ^(E0

( H ^s ν , E ^s ν ) = O ( 1 ), ρ= N ^ρ

x 2 + y 2 , ρ→∞ , z =± 0.

Здесь { E v , H v } – полные поля в D v , v =0, 1, i , s , соответственно, k = ω / c , n i , s , – единичные нормали к поверхностям ∂ D i , s , e z – нормаль к подложке, а характеристики среды выбраны таким образом, что Im ε 0,1, i =0, Im ε s ≤ 0, Im ε L ≤ 0. Предполагается, что временная зависимость выбрана в виде exp{ j ω t }.

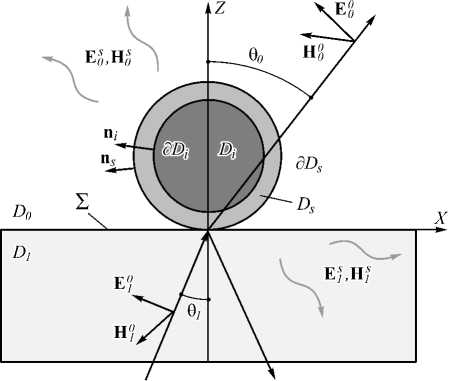
Рис. 1. Геометрия задачи: плоская волна падает под углом θ1 из диэлектрической призмы D1 на частицу, состоящую из ядра Di и металлической оболочки Ds , θ0 – угол преломления; {E0ν,H0ν} – поле плоской и {Eνs ,Hνs }, v=0,1, – поле рассеянной волны в верхнем полупространстве и призме

Конкретизируем остальные величины, входящие в постановку задачи (4). Поля { E 0ν , H 0ν }, ν= 0,1, представляют собой результат решения задачи отражения и преломления поля плоской волны { E ⁰, H ⁰} на поверхности раздела полупространств Σ. { E ^s ν , H ν ^s }, ν = 0,1, есть рассеянные поля в каждом из полупространств, которые определяются как E ^s _ν= E _ν- E _ν ⁰ , H V = H _v - H 0 , v = 0,1. В силу построения поля внешнего возбуждения и граничных условий на Σ рассеянное поле { E V , H V }, v = 0,1, также должно удовлетворять условиям сопряжения для тангенциальных компонент на плоскости Σ.

На поверхностях ∂ D i , s в дополнение к классическим условиям сопряжения поставлены дополнительные условия для нормальных компонент полей, необходимые для однозначной разрешимости задачи. Эти условия физически соответствуют условиям обращения в нуль нормальной компоненты тока проводимости на границах раздела металл-диэлектрик n ⋅ J =0, которые затем трансформируются в условия для нормальных компонент полей [17]. Условия излучения задачи (4) сформулированы таким образом, чтобы обеспечить обращение в нуль потока энергии на бесконечности для однородной задачи (4). Мы будем полагать, что поставленная граничная задача (4) имеет единственное классическое решение.

Параметры ξ и ε L , относящиеся к продольному полю E _s ^L , определяются следующим образом

ε L =ε s -ω ² p ( j γω-ω ² ) ,

ξ ² =ε s ( β ² + D ( γ+ j ω ))/( ω ² - j γω ) .

Здесь ω p – плазменная частота металла, γ – коэффициент затухания, β – гидродинамическая скорость в плазме, связанная со скоростью Ферми v F соотношением β ² = 3/5 v_F ² , D – коэффициент диффузии электронов [17].

Метод дискретных источников с учетом призмы и модели ОНО

Обозначим { E ⁰, H ⁰} поле плоской электромагнитной волны линейной поляризации, распространяющейся из нижнего полупространства в полуплоскости ϕ = π , которое образует угол θ 1 с осью Oz, направленной из D 1 в D 0 . Будем строить приближенное решение задачи (4), руководствуясь схемой [24]. Ограничимся случаем Р-поляризации, поскольку именно она реализует наибольшую амплитуду плазмонного резонанса. Так как частица целиком располагается в верхнем полупространстве D 0 , то поле преломленной волны { E ⁰ ₀, H ⁰ ₀} приобретает вид

E ⁰ ₀( M ) = T ^P ( - e _x cos θ ₀ + e _z sin θ ₀) ×

× exp{ - jk ₀( x sin θ ₀ + z cos θ ₀)},                    ₍₅₎

H00(M) =TPn0ey exp{-jk0(xsinθ0+zcosθ0)}, где n0=ε0, T P – коэффициент преломления Френеля [25], а ex, ey, ez – единичные векторы декартовой системы координат. В соответствии с законом Снеллиуса: n0 sin θ0 = n1 sin θ1, n1=ε1. Таким образом, преломленный угол θ0 = arc sin(n1 / n0 ⋅ sinθ1). В случае, когда волна падает из более плотной среды в менее плотную n1 > n0, существует угол полного внутреннего отражения θс =arc sin(n0 / n1), за которым волна не проходит в верхнее полупространство, так как полностью отражается от поверхности Σ. При этом энергия распространяется вдоль поверхности раздела полупространств и экспоненциально затухает в перпендикулярном направлении. В этом случае sin θ0 > 1 (угол θ0 оказывается комплексным), cos θ0 в этом случае принимает значение cos θ0=-j sin2 θ0-1 , а амплитуда плоской волны в D0 приобретает вид exp {-jk0xsin θ0} exp {-k0z sin2 θ0-1

Построим приближенное решение задачи (4) для рассеянного поля в D0 с учетом осевой симметрии и поляризации, удовлетворяя квазиклассической системе уравнений Максвелла во всех областях постоянства параметров среды, условиям излучения и условиям сопряжения для полей на 5. В основу представления для рассеянного поля положим Фурье-компоненты тензора Грина полупространства, которые могут быть записаны в виде интегральных представлений Вейля–Зоммерфельда [18]

от

G m , h ( Z , Z n ) = J J m ( Xp ) v fih ( X , z , Z n ) X ^{1 + m} d X , 0

от gm’h (Z, Zn ) = J Jm (Xp) V£h (X, Z, Zn ) X1+mdX .

Здесь J m (.) - цилиндрическая функция Бесселя, точка Z = ( p , z ) располагается в полуплоскости ф = const, а точки локализации мультиполей распределены вдоль оси симметрии z_n е OZ строго внутри D i и D s . Спектральные функции электрического и магнитного типов обеспечивают выполнение условий сопряжения на границе интерфейса z =0. В данном

случае для них справедливы следующие выражения

V 1 e 1 h ( X , Z , Z n ) =^	e -n°| z - zn\ + A e . h ( X ) e -nol Z + z n l	z >  o,
	n o „ П 1 z -n o z n B nh ( X ) e ------, Z <  o, n o
v 31h ( X , z , Z n ) = ^	' A 3 e 1 h ( X ) e ~no ( Z + z n ’ , z >  o,	(7)
	B 3 e 1 h ( X ) e n 1 Z -n o Z o , Z <  o,

где z n >0, а спектральные коэффициенты A , B определяются из одномерной задачи с условиями сопряжения при z =0, откуда легко получается, что

e , h        e , h

A ll ’ h ( X ) =       - 14 B Bn ’ h ( X )

¹¹ e , h       e , h      ¹¹

L o  ⁺ Л 1

2 x o’

x O’ h + x e

' G m ( Z , z e )sin( m + 1) ф ^

A m^hn ^)o =   G m ( Z , Z n )cos( m + 1) ф   .                 (8)

.- g m +1 ( Z , Z n )sin( m + 1) ф_у

Для построения полей внутри областей D i , s будут

использоваться следующие потенциалы

' Y m ( Z , z v )cos( m + 1)ф ^A

A ( e ’v mn

A ⁽ h ’ ^v mn

- Y m ( Z , Z n ) sin( m + 1) ф , A n ^{) v} =

' Y m ( Z , z v )sin( m + 1) ф^А Y m ( Z , z v )cos( m + 1) ф . o .

Y m ^{( Z} , z n ’ = j m ⁽ k i r Zz n ⁾⁽p/ ^r Zz n ’ ^m ’

A e, h ( X ) =  -------²⁵--------

( x o +x e )( x h +x h )

5 = VS o - 1 6 1 ,

B 31 h ( X ) = 1 1, ^S

V  S o

( x 0 + x i )( x o h +x h )

где

n = д/X ² - k v² , x V = n , x V =4v/S v , v = o,1.

При построении приближенного решения для рассеянного поля в D 0 используются векторные потенциалы, которые в цилиндрической системе координат записываются как

' G m ( Z , Z e )cos( m + 1) ф ^ A men⁰ = - G m ( Z , Z n )sin( m + 1) ф , - g m ( Z , Z n )cos( m + 1) ф.

A

( e )0 0 n

f ^o 1

o

. G h ( Z x) _?

f ^o ) ^o

. Y v( Z , Z n )J

v = i , s ± ,

Y m^{s ± ( Z} , z n ’ = h m ²-¹’ ⁽ k s^ , ⁾⁽ p/ ^r Z z , ) m ’

где jm (.) – сферическая функция Бесселя, hm(2,1) (.) – сферическая функция Ханкеля, индексы s ± соответствуют «уходящим» (+) и «приходящим» (–) волнам, rZ2zn = p2 + (Z - Zn )2, ki,s = ky/si^ ,

z_n ^{i , s} – координаты дискретных источников (ДИ). Следует отметить, что функции, положенные в основу векторных потенциалов (8–9), удовлетворяют уравнению Гельмгольца (2).

В случае Р-поляризации продольное поле строится на основе скалярных потенциалов [21]

^ m±n ( M ) = h^ ( k L R Z z n ) P^ (cos 6 z n ) cos( m + 1) ф ,

T n ± (M) = ho2-1’( kLR Zzn), удовлетворяющих уравнению Гельмгольца (3). Здесь Pmm+1(cos 6) = sinm 6 . Тогда приближенное решение для полного поля внутри частицы и рассеянного в D0, соответствующее Р-поляризации, принимает следующий вид

E ² N =

= ]L S Ym n-j-r«trolAmn + qmn 1 rot As 1 + m=o n=1 ^     k Sv

Nv0

+V r „"---- rot rot A ( e ’ ^v,

^Si k S v

M NsmN

E LN = SS Psnngrad T m±n +S rnss ± grad T n1, m=o n=1

HN = j-^rotEN, v= o,i,s±.(Ю)

k

Заметим, что внутри оболочки D s электромагнитное поле строится как сумма «уходящих» и «приходящих» волн, то есть

NTNTNLNLN s -^s + + -^s- + -^s + + -^s- , divEsN = o, rotEL± = o.

Построенные поля (10) удовлетворяют квазиклас-сической системе уравнений Максвелла граничной задачи (4) и условиям сопряжения на бесконечной поверхности подложки Σ. А неизвестные амплитуды ДИ { p m ^ν n , q m ^ν n , r n ^ν ; p m^{s ±} n , r n^{s ±} } определяются из условий сопряжения на поверхностях ∂ D i , s . Численный алгоритм строится по стандартной схеме, изложенной в [18] с учетом особенностей поведения продольного и поперечного волновых чисел [22].

Для вычисления характеристик рассеяния в дальней зоне нам понадобится диаграмма рассеяния F ( θ , ϕ ), которая определяется в верхнем и нижнем полупространствах как

E 0 ^s ,1 ( r ) ₌

I E⁰ ( z = 0) ⁼

= ^{exp{ - jk 0,1 r }} F ^(0,1) ( θ , ϕ ) + O (1 r ² ), r →∞ . r

Компоненты диаграммы на единичной верхней полусфере Ω + = {0 ≤θ≤π /2;0 ≤ϕ≤ 2 π } в случае Р-поля-ризации принимают вид

MN

Fθ(0)(θ,ϕ)=jk0∑cos((m+1)ϕ)(jsinθ)m∑{pn0m× m=0

e(0)                      e(0)

×[Gncosθ+jk0gn sin2θ]+qn0mGn}-

N 0⁰

k0

- j sin θ ∑ r n ⁰ G n ,

ε0

MN

Fϕ(0)(θ,ϕ)=-jk0∑sin((m+1)ϕ)(jsinθ)m∑{pn0m × m=0

× Gen(0) +qn0m[Ghn(0)cosθ+jk0ghn(0)sin2θ]}, где соответствующие спектральные функции Gne,h, gnh могут быть представлены в виде

G ^e _n ^{, h (0)} ( _θ ) ₌ A₁ e ₁ , h ( k ₀sin _θ ) _⋅ e - jk 0 z n cosθ ₊ e jk 0 z n cosθ , g ^en ^{, h (0)} ( θ ) = jk 0 cos θ A 3 ^e 1^{, h} ( k 0 sin θ ) ⋅ e ^{- jk 0 zn cos θ} , z n > 0.

В нижнем полупространстве

Ω- ={π/2≤θ≤π;0≤ϕ≤2π} компоненты диаграммы имеют вид

MN

Fθ(1)(θ,ϕ)=(jk∑(jk1 sinθ)mcos(m+1)ϕ∑{pn0m × m=0

×[Gne(1)cosθ+jk1sin2θgne(1)]+qn0mGnh(1)}-

N 0

- jksinθ∑ rn0Gne(1)) I cos θ I , n=1

Fϕ(1)(θ,ϕ)=-jkcosθ∑M (jk1sinθ)msin(m +1)ϕ × m=0

N m

×∑{pn0m⋅Gne(1)+qn0m[Gnh(1)cosθ+jk1sin2θgnh(1)]}, n=1

где спектральные функции G_n ^{e , h (1)} , g _n ^{e , h (1)} записываются следующим образом

G n^{e , h (1)} ( θ ) = ( k 1 , jk ) ⋅ B 1 ^e 1^{, h} ( k 1 sin θ ) ⋅ e ^{- jk} ( ^{1 -ε 1 sin 2 θ} ) ^zn , g n^{e , h (1)} ( θ ) = ( k 1 , jk ) ⋅ B 3 ^e 1 ( k 1 sin θ ) ⋅ e ^{- jk} ( ^{1 -ε 1 sin 2 θ} ) ^zn .

Определив амплитуды ДИ для рассеянного поля, можно легко вычислить компоненты диаграммы рассеяния (12– 13) всюду на единичной сфере, а также поле (10) в непосредственной близости от частицы. Следует подчеркнуть, что диаграмма рассеяния во всем пространстве вычисляется на основе одних и тех же амплитуд ДИ { p_n ⁰ _m , q_n ⁰ _m , r_n ⁰ } , что является следствием использования тензора Грина, реализующего единое представление для рассеянного поля всюду в D 0,1 .

Численные результаты

Будем рассматривать слоистую сферическую частицу с фиксированным диаметром ядра D = 16 нм, состоящею из SiO 2 с показателем преломления n i = 1,46, и золотой оболочкой, толщину которой обозначим как d . Пусть частица располагается на стеклянной призме BK7 с показателем преломления n 1 = 1,52 в активной среде R6G с n 0 = 1,326. В данном случае критический угол θ c = 60,735 ° . В расчетах частотная дисперсия золота учитывается в соответствии с экспериментальными результатами [26].

Нас будут интересовать интенсивность рассеяния в дальней зоне

σ ⁰ sc ^,1 ( θ 1 , λ ) =

⁼ ∫ ( F θ^(0,1) ( θ 1 , θ , ϕ ) ² + F ϕ^(0,1) ( θ 1 , θ , ϕ ) ² ) d ω Ω^±

и характеристики поля в непосредственной близости от внешней оболочки слоя ∂ D s , в том числе интегральный коэффициент усиления (ИКУ) интенсивности поля

E ( θ 1 , λ ) = ∫ E 0 ^N + E 0⁰² d σ / ∫ E ⁰0² d σ ,          (15)

∂Ds                       ∂Ds и сечение поглощения

σ abs ( θ 1 , λ ) =- Re ∫ ( E 0 ^N + E ⁰0 ) × ( H 0 ^N + H ⁰0 ) ^∗ d σ .

∂ D s

Величины σ s 0 c ,1 и σ abs имеют размерность мкм 2 .

Поскольку в рамках выбранной схемы генерация вторичного излучения происходит в активной среде, то основной характеристикой будет служить коэффициент усиления E ( θ 1 , λ ). Кроме того, мы по аналогии с задачами флюоресценции введем в рассмотрение аналог квантового выхода резонатора [27], который фиксирует отношение «полезного» излучения к «потерянной энергии». В качестве потерь мы будем рассматривать как поглощенную энергию σ abs , так и энергию, рассеянную в призму σ 1 sc . Таким образом, квантовый выход резонатора (КВР) определим как

к (9_ь X ) = E ( 9 1 , X )     ° sc    .                       (16)

°. + ° abs

Перейдем к анализу влияния ЭН на коэффициент усиления (15) и квантовый выход (16). Для золота соответствующие квантовые параметры, необходимые для вычисления нелокальных величин sL и kL, выбраны в соответствии с [28], то есть йюp = 9,03 эВ, йу = 0,053 эВ, vF = 1,40-1012мкм/с, D = 8,62-10sмкм2/с.

Задавая длину волны внешнего возбуждения λ и вычисляя соответствующее значение ю , легко определить значения нелокальных параметров s L и k_L .

На рис. 2а, б приведены сравнительные результаты для интегрального коэффициента усиления интенсивности (15) при возбуждении неизлучающей вол- ной, падающей из призмы с углом 91 = 62°, и волной, наклонно падающей из верхнего полупространства под углом 9’ = 47° для различных толщин золотой пленки d = 2,5, 1,5 нм. Видно, что использование неизлучающего поля ведет к увеличению ИКУ для обеих толщин. Кроме того, учет ЭН приводит к существенному снижению амплитуды с одновременным небольшим сдвигом в коротковолновую область.

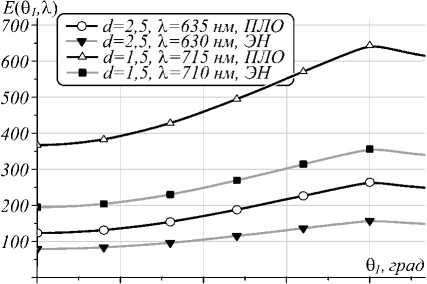
Выбор углов падения волны можно объяснить, анализируя результаты, представленные на рис. 3 а , б , где для длин волн, соответствующих плазмонному резонансу, приведены ИКУ в зависимости от угла.

На рис. 3 а максимум достигается вблизи критического угла 9 с = 60,735 ° . На рис. 3 б можно видеть монотонное возрастание ИКУ. Вместе с тем рост за углом 9’ = 47 ° обусловлен уменьшением величины знаменателя в (15).

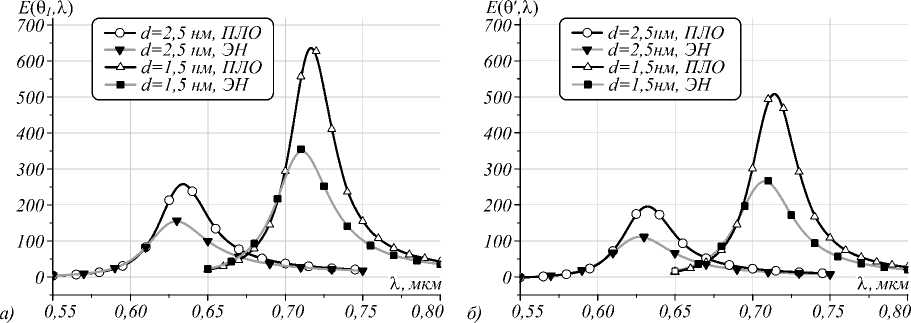
Рис. 2. Зависимость ИКУ (15) от длины волны при углах падения 6 1 = 62° (а) и 6’ = 47° (б) для частицы диаметром D = 16 нм с золотой оболочкой толщиной 1,5 и 2,5 нм с учётом эффекта нелокальности и в приближении локального отклика (ПЛО)

а)

15       30       45       60

ХХО'Л)

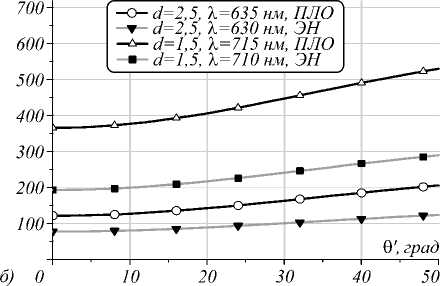
Рис. 3. Зависимость ИКУ (15) от угла падения при возбуждении из призмы (а) и сверху (б) частицы диаметром D = 16 нм в золотой оболочке толщиной 1,5 и 2,5 нм для различных длин волн с учётом эффекта нелокальности и в приближении локального отклика

Рис. 4 а , б демонстрируют результаты расчета квантового выхода.

В данном случае следует отметить, что неизлучающая волна реализует квантовый выход с увеличенной амплитудой. При этом учет ЭН приводит к его снижению в 2–2,5 раза с незначительным смещением в сторону коротких волн.

Аналогичные предыдущему результаты можно видеть на рис. 5 а , б .

Заключение

На основе компьютерной реализации модели 3D-резонатора плазмонного нанолазера исследовано влияние эффекта нелокальности на интегральный коэф- фициент усиления интенсивности ближнего поля и квантовый выход резонатора. Показано, что возбуждение неизлучающей волной реализует большие значения как коэффициента усиления, так и квантового выхода. При этом учет эффекта нелокальности приводит к существенному снижению интенсивности в 2–2,5 раза, а положение плазмонного резонанса незначительно смещается в область коротких волн.

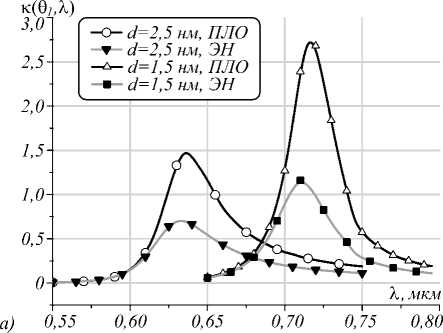
Рис. 4. Зависимость КВР(16) от длины волны при углах падения θ 1 =62° (а) и θ’=47° (б) для частицы диаметром D=16 нм в золотой оболочке толщиной 1,5 и 2,5 нм с учётом эффекта нелокальности и в приближении локального отклика

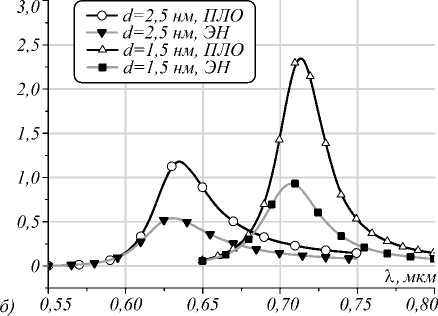
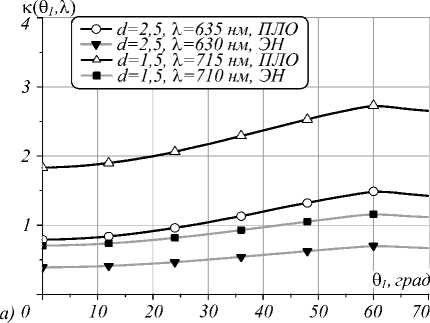
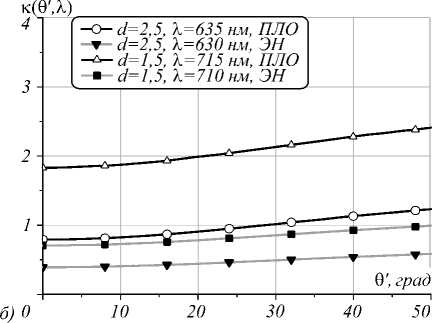
Рис. 5. Зависимость КВР (16) от угла падения при возбуждении частицы диаметром D=16 нм в золотой плёнке толщиной 1,5 и 2,5 нм из призмы (а) и сверху (б) для различных длин волн с учётом эффекта нелокальности и в приближении локального отклика

Смещение в область коротких волн обусловлено дополнительными граничными условиями на поверхности. Они «вдавливают» электронное облако внутрь, как бы меняя границы плазмонного металла. Если их заменить на классические условия для скачка нормальной компоненты смещения, то максимум вернется на прежнее место [22]. Что касается снижения интенсивности, то это чисто квантовый эффект нело-кальности, т.е. учет коллективного взаимодействия электронов, который, кроме того, вызывает появление дополнительных зарядов на поверхности раздела сред, экранирующих излучение [30]. Эффект нело-кальности проявляется в диапазоне плазмонного резонанса при достаточной плотности носителей заряда. Например, в случае полупроводника ZrN или TiN этот эффект сдвигается в инфракрасную область, а для InSb и GaAs – в микроволновую [31].

Полученные результаты имеют непосредственное отношение к проектированию современных нано-плазмонных устройств.

Работа выполнена при финансовой поддержке Московского центра фундаментальной и прикладной математики (проект «Моделирование элементов плазмонного нанолазера с учетом квантовой нелокальности»).