Численный анализ контактного напряженного состояния опорных частей с шаровым сегментом

обеспечивают горизонтальные возвратнопоступательные перемещения опорного узла в двух взаимно-перпендикулярных направлениях. Общим для всех типов конструкции опорных частей с шаровым сегментом (рис. 1) является верхняя плита с шаровым полированным сегментом – 1 , нижняя плита со сферическим вырезом – 2 и прослойка из антифрикционного материала (сферическая поверхность скольжения) – 3.

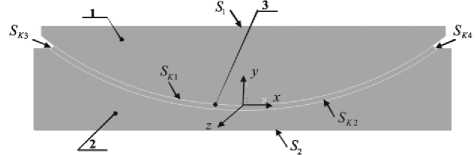
Рис. 1. Схема конструкции опорной части с шаровым сегментом

Настоящая работа направлена на изучение напряженно-деформированного состояния данных частей конструкции и исследование поведения антифрикционного материала сферической поверхности скольжения. Рассматриваются 2 реальные конструкции опорных частей пролетных строений мостов с шаровым сегментом л-250 и л-350, отличающиеся радиусом шарового сегмента и соответственно радиусом сферического выреза – изготовленные ООО «АльфаТех» по проектам и с научнотехническим сопровождением ООО «Ко Люмьер Лтд» (г. Москва).

Математическая постановка. Математическая постановка упругого поведения материала включает в себя уравнения равновесия [2]:

div ° — 0 x _е V

,

геометрические соотношения

ё — 1 (v u +(v u )П  _ _TZ

2             x е V

,

С n <  ⁰ , ^a n a^— q ^a n , u n — u 2 , ^{u 1} ^ ^u 2 ,  (7)

где q - коэффициент трения, u_n - нормальные смещения, индекс a=1, 2, (1, 2 - условные номера двух контактирующих поверхностей;

- отлипание

физические соотношения

с — X I₁ ( ё ) I + 2 цё   X е V u V

,

где X и ц - параметры Ламе, I (^ё)

- первый

|^u n - ^un ²| ^ ⁰ , ^a n a ^—a n ^{— 0} , a— ^1,2 ,        (8)

- полное сцепление u1 - u2 — 0 , a na—a n — 0 , a —1,2 .          (8)

инвариант тензора деформаций, I - единичный тензор.

Для описания поведения материала прослойки выбрана деформационная теория пластичности, физические соотношения которой имеют вид [3]:

₆^— ^( ^{ё- I (s)} I ^{) + 3} K^{I (s} ) I X е V ,

где a _u — ^3 1 ₂ ( С ) - интенсивность тензора напряжений ( I ₂ ( ° ) - второй инвариант тензора

напряжений), s — -2= ^ I ( ё ) ^u 3²

–

интенсивность

Идентификация определяющих уравнений. При определении напряженно-деформированного состояния опорных частей с шаровым сегментом одним из главных этапов исследования является изучение поведения материалов антифрикционной прослойки. Для этого были проведены натурные эксперименты на одноосное сжатие, направленные на изучение поведения материалов на основе фторопласта-4 (эксперименты проведены в ИМСС УрО РАН д.ф.-м.н. Адамовым А.А.). Эксперименты проводились на цилиндрических образцах с диаметром 20 мм, высота равна диаметру (рис. 2).

тензора деформаций ( I ₂ ( ё ) - второй инвариант тензора деформаций), K - объемный модуль упругости, o u = Ф(s u ) - функциональная зависимость, определяемая кривой деформирования.

Математическая постановка дополняется кинематическими граничными условиями на поверхности S2

^u y ^{— 0} X е S^ ,

и статическими граничными условиями на поверхности S 1

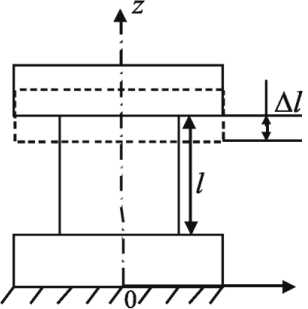
Рис. 2. Схема эксперимента

6 ■ n — P ^{x е S} 1

остальные наружные поверхности являются свободными

a ■ n — 0

.

Система уравнений (1) - (4) дополняется граничными условиями на поверхности контакта  Sk  Sk 1 u Sk2 u Sk3 u Sk4 . Рассмат риваются следующие типы контактного взаимодействия:

- проскальзывание с трением: для трения покоя

С n <  0, ^a n a < q ^a n , u ¹ — u ²,  (7)

для трения скольжения

Образцы изготовлены из материалов: фторопласт-4 - мат. 1, антифрикционный композиционный материал на основе фторопласт-4 со сферическими бронзовыми включениями - мат. 2, и модифицированный фторопласт (фторопласт-4 без наполнителя после облучения) - мат. 3. На основе анализа результатов экспериментов в качестве модели поведения материала была выбрана деформационная теория упругопластичности [3]. Проведена серия численных экспериментов с использованием программного комплекса ANSYS, направленных на проверку работоспособности выбранной модели поведения материала. В рамках численного эксперимента происходит имитация

условий натурного эксперимента с использованием деформационной теории упругопластичности, параметры которой определены из натурного эксперимента. Реализована трехмерная контактная задача, включающая в себя уравнения (1), (2) и (4), боковые грани свободны, на контактных поверхностях заданы условия контактного взаимодействия с учетом трения (6)-(9), коэффициент трения q=0,04, нижняя плита пресса неподвижна, к верхней плите прикладывается возрастающее по величине вертикальное перемещение uz=Δl (рис. 2). По результатам численного решения задачи о деформировании образца определялись поля средних по сечению образца z=l/2 напряжений σz и деформаций εz  и строились диаграм мы деформирования. На рис. 3 представлены результаты сравнения экспериментально полученных диаграмм деформирования и их численного прогнозирования для случаев мат. 1, мат. 2 и мат. 3.

Установлено, что для всех материалов численный расчет с использованием выбранных определяющих соотношений дает хорошее количественное соответствие результатам эксперимента.

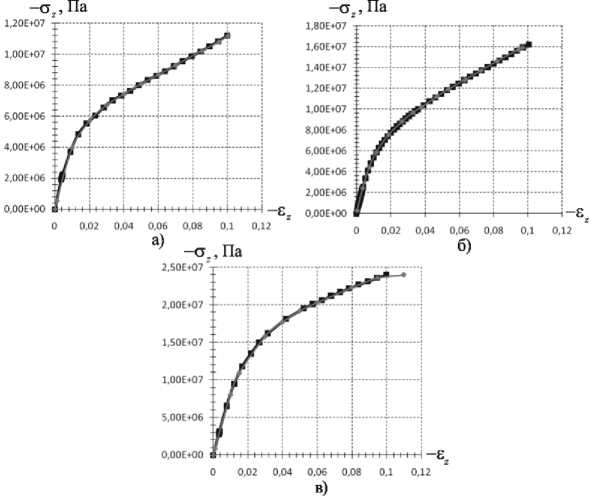
Рис. 3. Диаграммы сжатия σ – ε ( натурный, численный эксперименты): а) мат.1; б) мат. 2; в) мат. 3

Реализация решения и полученные результаты. Реализовано решение трехмерной контактной задачи, описанной в 1, для конструкций опорных частей с шаровым сегментом пролетных строений мостов л-250 и л-350. При помощи программного комплекса ANSYS построены трехмерные конечно-элементные модели с использованием деформационной теории упругопластичности. В конечноэлементной реализации используется элемент в виде 4-х узлового тетраэдра, обладающий линейной аппроксимацией и 3 неизвестными в каждом узле. В прослойке произведено сгущение размера элемента, в нижней и верхней плитах размер элементов градиентно увеличивается. Общее количество элементов и узлов в модели л-250 – 299258 и 56596, л-350 – 675840 и 121792 соответственно. На поверхностях соприкосновения верхней и нижней плит с прослойкой нанесена контактная конечно элементная пара, позволяющая учесть трение.

Изучены особенности напряженно-деформированного состояния конструкций и поведения антифрикционного материала прослойки. На модель наложены статические и кинематические граничные условия, соответствующие реальной максимальной нагрузке при эксплуатации опорной части с шаровым сегментом в пролетных строениях мостов: к верхней плите прикладывается распределенная вертикальная и горизонтальная нагрузка – для л-250 54 МПа и 7 МПа, для л-350 76 МПа и 7 МПа соответственно. Рассматривалось совместное действие вертикальной и горизонтальной нагрузок (нагружение 1) и действие только вертикальной нагрузки (нагружение 2).

Для трех материалов прослойки опорных частей с шаровым сегментом при заданных нагрузках получены поля интенсивности напряжений, линейных, сдвиговых и объемных деформаций, перемещений в прослойке, характер контактного взаимодействия, контактное давление, характер перемещений в нижней плите.

Зоны контактного взаимодействия между прослойкой и плитами качественно одинаковы для мат. 2 и мат. 3. При совместном действии вертикальной и горизонтальной нагрузок результаты представлены на рис. 4, при действии только вертикальной – рис. 5.

При одновременном действии сдвиговой и вертикальной нагрузки в конструкциях л-250 и л-350 разъединение контактных поверхностей не происходит. В случае л-250 преобладает проскальзывание, имеет место сцепление с наиболее нагруженной стороны (по направлению действия сдвигающей нагрузки). В случае л-350 вертикальная составляющая нагрузки больше, преобладает сцепление на нижней и верхней контактных поверхностях прослойки. При действии только вертикальной нагрузки разъединение контактных поверхностей также не происходит. На основной доле площади поверхности преобладает смыкание.

Результаты решения задачи для прослойки, изготовленной из мат. 1 обладают особенностью: на торцевой поверхности прослойки присутствуют локальные зоны раскрытия контакта (рис. 6). При нагружении 1 в конструкции л-350 присутствует проскальзывание и смыкание контактных поверхностей на верхней и нижней поверхностях прослойки. В остальном, характер статусов контакта значительно не изменился.

Рис. 4. Зоны контакта при нагружении 1 ( проскальзывание, сцепление): а),б) – л-250 и в),г) – л-350; а), в) – вид сверху, б), г) – вид снизу на контактные поверхности прослойки

5)                                                 г)

Рис. 5. Зоны контакта при нагружении 2 ( проскальзывание,

смыкание):

а),б) – л-250 и в),г) – л-350; а), в) – вид сверху, б), г) – вид снизу на контактные поверхности прослойки

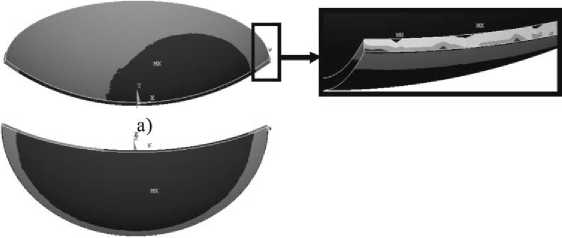
б)

Рис. 6. Зоны контакта для мат. 1, конструкция л-350, нагружение 1

( отлипание, около контактное, проскальзывание, смыкание): а) – вид сверху, б) – вид снизу на контактные поверхности прослойки

В зоне контакта действуют контактные давление (рис. 7) и касательное напряжение (рис. 8). Наибольший интерес представляют данные величины на контактной поверхности прослойки, обладающей большей свободой SK1. Контактные давления и напряжения трения построены по поверхности прослойки SK1 в сечениях z=0 и x=0. В случае совместного действия вертикальной и горизонтальной нагрузок контактное давление возрастает по направлению действия сдвигающей нагрузки. На краю прослойки контактное давление для соседних узлов может отличаться на порядки. Данная ситуация может быть связана с переходом от одной зоны проскальзывания к зоне смыкания. В случае действия только вертикальной нагрузки контактное давление на концах прослойки минимально. Картина распределения контактного давления более ровная. Для конструкции л-250 заметно скачкообразное изменение контактного давления в близи края прослойки. Следует отметить, что контактное давление меньше, по сравнению с другими материалами, и более равномерно распределено у материала 3.

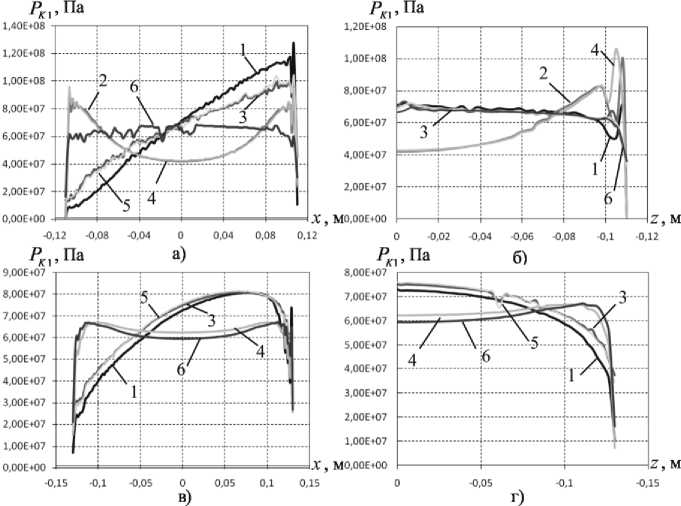
Рис. 7. Контактное давление на S :а),б) – л-250 и в),г) – л-350: 1 – мат. 1, нагружение 1; 2 – мат. 1, нагружение 2; 3 – мат. 2, нагружение 1; 4 – мат. 2, нагружение 2; 5 – мат. 3, нагружение 1; 6 – мат. 3, нагружение 2

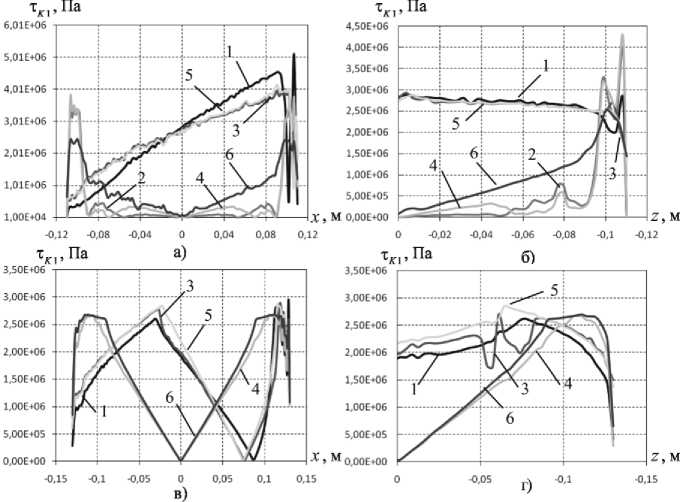
Рис. 8. Контактное касательное напряжение на S K 1 :

а),б) – л-250 и в),г) – л-350: 1 – мат. 1, нагружение 1; 2 – мат. 1, нагружение 2; 3 – мат. 2, нагружение 1; 4 – мат. 2, нагружение 2; 5 – мат. 3, нагружение 1; 6 – мат. 3, нагружение 2

Касательное контактное напряжение на порядки меньше чем контактное давление и дает малый вклад в полное контактное напряжение. В случае совместного действия вертикальной и горизонтальной нагрузки для конструкции л-250 характер распределения контактного напряжения аналогичен контактному давлению, для л-350 возрастает по направлению действия сдвигающей нагрузки при нахождении в зоне проскальзывания, затем снижается до нуля в зоне смыкания и начинает снова возрастать к зоне проскальзывания. В случае действия только вертикальной нагрузки напряжения трения для л-250 минимальны на большей доли поверхности, что связанно с преобладанием зоны смыкания, у л-350 зона смыкания меньше – контактное касательное напряжение возрастает в зонах проскальзывания, снижаясь до нуля в зоне смыкания, на краях прослойки напряжение трения мало. Распределение контактного напряжения трения равномерней у материала 3.

Выводы: на основе численного решения трехмерной контактной задачи упругопластичности изучены картины распределения зон разного типа контактного взаимодействия. Установлены величины и характер распределения контактного давления и контактного касательного напряжения на поверхности контакта. Отмечено, что использование для изготовления прослойки материала 3 (модифицированный фторопласт) обеспечивает более благоприятные условия работы исследуемого узла.