Численный анализ субволновой фокусировки с помощью кремниевого цилиндра

Одним из эффективных применений дифракционных микроэлементов является фокусировка лазерного излучения в ближней зоне дифракции. Известно применение для острой фокусировки массивов из простых микроэлементов (микроцилиндры, микроотверстия) [1 –3], с помощью которых удалось добиться размера фокального пятна по полуспаду интенсивности (FWHM) вплоть до 0,38λ [2]. Исследование дифракции Гауссова пучка на отдельном цилиндре с субволновым радиусом (показатель преломления n = 2,0) показывает, что можно добиться уменьшения размера пятна по FWHM до 0,36λ [4]. В [5] было продемонстрировано, что микровыступ обладает лучшими фокусирующими свойствами, чем микроотверстие.

Как было показано в [6], радиальная поляризация обеспечивает максимальное отношение интенсивности продольной компоненты к интенсивности поперечных компонент при острой фокусировке. Однако учитывая определённые проблемы генерации радиальной поляризации – необходимость использования сложных или дорогостоящих устройств, в работах [7–8] была рассмотрена возможность возбуждения продольной компоненты при фокусировке однородно-поляризованного излучения за счёт внесение фазовой сингулярности в падающий пучок. Такая возможность была экспериментально подтверждена в [9]. В упомянутых работах рассматривались фокусирующие элементы с показателем преломления n = 1,46. Увеличение показателя преломления позволит [8] добиться увеличения вклада продольной компоненты в картину общей интенсивности на оптической оси.

В качестве элемента с высоким показателем преломления в работе рассматривается кремний (Si), который является вторым по распространённости элементом (после кислорода) в земной коре. В настоящее время кремний и его соединения имеют разнообразные области применения, в частности, используются для изготовления полупроводниковых приборов (инте- гральных схем, диодов, транзисторов) [10– 11], солнечных батарей [12], в биологии и медицине [13]. В работе [14] для 2D микролинзы Микаэляна, изготовленной из кремния с показателем преломления 3,47, вблизи поверхности линзы было получено фокальное пятно 0,12λ по полуспаду интенсивности (FWHM).

В данной работе проведены исследования по влиянию изменения радиуса (в диапазоне от 0,25λ до 2λ) кремниевого цилиндра на картину дифракции Гауссова пучка и лазерного пучка с вихревой фазовой сингулярностью первого порядка. Численные расчёты выполнены на основе конечно-разностного временного метода (FDTD), реализованного в программном продукте MEEP [15]. Рассмотрена круговая поляризация лазерного излучения, направление которой противоположно направлению вихревой фазовой сингулярности.

Дифракция Гауссовых пучков

Численное моделирование производилось с использованием вычислительного кластера мощностью 775 GFlops. Характеристики кластера: количество ядер – 116, вычислительные узлы – 7 сдвоенных серверов HP ProLiant 2×BL220c, объём RAM – 112 Гб.

Параметры моделирования: длина волны излучения λ = 1,55 мкм, размер расчётной области x , y, z ∈ [–9 λ ; 9 λ ]. Толщина поглощающего слоя PML – 0,66 λ , шаг дискретизации по пространству – λ /31, шаг дискретизации по времени – λ /(62 c ), где c – скорость света. Источник находится внутри подложки, на расстоянии 0,1 мкм перед началом рельефа. Подложка занимает всё пространство до PML (погружена в PML на 0,5 мкм). Показатель преломления n равен 3,47. Высота выступа равнялась 1,55 λ .

Исследования проводились для двух типов лазерных пучков, которые могут быть сгенерированы в лазерных резонаторах и сохраняют свою структуру при распространении в свободном пространстве при круговой поляризации лазерного излучения: Гауссова пучка и моды Га-усса–Лагерра (0,1). Внешний вид рассматриваемых пучков приведён на рис. 1. Радиус пучка σ = 1,5λ.

б)

Рис. 1. Входные пучки: интенсивность Гауссова пучка (а), интенсивность моды Гаусса–Лагерра (0,1) (б), фаза моды Гаусса–Лагерра (0,1) (в)

В табл. 1 приводится распространение рассматриваемых лазерных пучков при прохождении через цилиндр с разным показателем преломления: 1,5 и 3,47. Радиус цилиндра максимален, по краям он частично вписан в поглощающий слой PML.

Изменение размера цилиндра

В дальнейших исследованиях будем рассматривать показатель преломления n = 3,47, соответствующий кремнию. Проведём исследование влияния изменения размера цилиндра на размер фокального пят- на для рассматриваемых Гауссовых пучков. Дифракция Гауссова пучка показана в табл. 2, где, кроме общей интенсивности, также отдельно приводится продольная компонента (z-компонента) электрического поля. Для фундаментальной Гауссовой моды z-компонента формируется вне оптической оси, и распределение имеет вид световой трубки. Также в табл. 2 приведены размеры фокальных пятен по полуспаду интенсивности в максимумах вне элемента.

Наилучший результат был получен при размере цилиндра 1,25λ. В этом случае в непосредственной близости от элемента формируется узкое фокальное пятно, размер которого по FWHM равен 0,25λ.

Следует отметить, что для ряда случаев ( r = 0,25λ, r = λ, r = 1,5λ) фокусировка происходит на некотором расстоянии от элемента, даже для случая r = 1,25λ после фокусировки рядом с элементом наблюдается значительное ослабление интенсивности на оптической оси.

Табл. 1. Дифракция на цилиндре с разным показателем преломления Гауссовых пучков, общая интенсивность (размер области - 10,32Х х 10,32Х)

Фундаментальная Гауссова мода
n = 1,5	n = 3,47
к 4Х б'х А iox	к к к к iox

Мода Гаусса–Лагерра (0,1)
n =1,5	n = 3,47
к к к А юх	к к к к iox

Табл. 2. Дифракция Гауссова пучка на цилиндре с субволновым радиусом при изменении радиуса цилиндра (размер области - 5,14Х х 5,84Х)

		r =0,25λ	r =0,5λ	r =0,75λ	r = λ	r = 1,25λ	r =1,5λ	r =2λ
			) о; Р) д) si		Z      Т>.     'Л            S1	1 У, XI. 41     5 л	/. ?л 1л 4л 5>	/.      ?Л      1Л     4/.      5>
н о m S В S VO О	-2Х -зх -4?. -5Х	«хе FWHM=0,69λ	. ..	FWHM=0,66λ	•X»: • FWHM=0,82λ	FWHM=0,25λ
сЗ К к о с S л ч о ч о с	- X -2Х -зх -4Х -5Х	=:		”1				:s

Для случаев r = 0,25λ и r = λ максимум формируется на расстоянии 0,19λ и 0,49λ соответственно. Для случая r = 0,75λ – непосредственно рядом с элементом. Отметим, что для всех рассматриваемых случаев глобальный максимум формируется внутри элемента. Для случая r = 1,25λ – на границе элемента и внешней среды.

Также следует отметить, что рост радиуса цилиндра приводит к формированию максимума продоль- ной компоненты электрического поля внутри оптического элемента, кроме случая r = 0,25λ.

Для перераспределения продольной компоненты электрического поля с периферии на оптическую ось внесём вихревую сингулярность первого порядка противоположного поляризации знака. В табл. 3 приведены аналогичные исследования по изменению радиуса цилиндра для моды Гаусса–Лагерра (0,1).

Табл. 3. Дифракция моды Гаусса–Лагерра (0,1) на цилиндре с субволновым радиусом при изменении радиуса цилиндра (размер области - 5,14Х х 7,66Х )

		r =0,25λ	r =0,5λ	r =0,75λ	r = λ	r = 1,25λ	r =1,5λ	r =2λ
		л     "'7     1л А/ 5л	i Г, 11    4) S)	1           1л 4л 1л	к 2а ЗХ 4Х 5Х	1     7>. 1л 41     11	1     7/. 1л 4л 11.	1       7).      11.     41.      11.
А Н о о к m S о к 0J Н В S § В ю О	- X -2л -Зл -4л	^
	- 6л
	-7л	FWHM = 0,67λ			FWHM = 0,29λ
cd Н К 0J К о к о к ^ о ES о к	-2л -Зл -4л -5л - 6л		ее»					• ее
	-7л	FWHM z =0,44λ			FWHM z = 0,26λ

Наилучший результат был получен при размере цилиндра λ. В этом случае рядом с элементом формируется узкое фокальное пятно, размер которого по FWHM равен 0,29λ.

Фокусировка вне элемента происходит также при размере цилиндра r = 0,25λ, максимум находится рядом с элементом. В остальных случаях глобальный максимум формируется внутри элемента. Отметим, в первый локальный максимум вне элемента попадает до 50 % интенсивности от глобального максимума.

Максимум продольной компоненты электрического поля также находится внутри оптического элемента, кроме случаев r =0,25λ и r = λ. Таким образом, по достижении некоторого критического радиуса (в данном случае r = λ) происходит фокусировка моды Гаусса–Лагерра (0,1) в узкое фокальное пятно, в основном состоящее из продольной компоненты электрического поля.

Следует отметить, что для малого размера цилиндра ( r = 0,25λ) как для Гауссова пучка, так и для моды Гаусса–Лагерра (0,1) происходит фокусировка вне элемента, хотя и в более широкое фокальное пятно.

Графики поперечных сечений интенсивности для моды Гаусса–Лагерра (0,1) (для случаев r = 0,25λ и r = λ) приведены на рис. 2, для Гауссова пучка – на рис. 3 (для случая r = 1,25λ).

Как видно из графиков на рис. 2, для случая r =0,25λ (рис. 2 а ) в картине общей интенсивности присутствуют значительные боковые лепестки, формируемые в основном поперечными компонентами электрического поля (>60 % от максимальной интенсивности). Для случая r = λ (рис. 2 б ) центральное фокальное пятно содержит в основном продольную компоненту электрического поля, амплитуда формируемых поперечными компонентами боковых лепестков составила ~20% от величины основного пика.

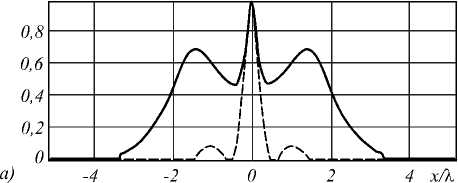
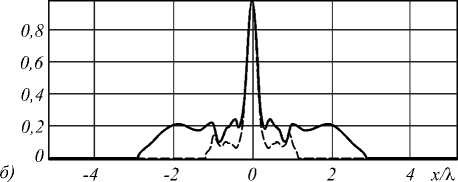
Рис. 2. Графики поперечных сечений в максимуме вне элемента, сплошной линией показана общая интенсивность, пунктирной – продольная компонента для моды Гаусса–Лагерра (0,1), радиус цилиндра равен 0,25λ (а) и λ (б)

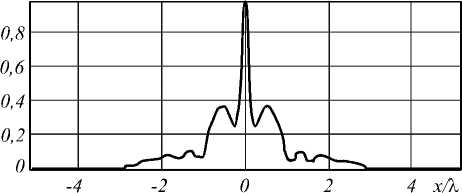
Рис. 3. График поперечного сечения общей интенсивности в максимуме вне элемента для моды Гаусса–Лагерра (0,1), радиус цилиндра равен 1,25λ

Заключение

Численно с помощью метода FDTD показано, что для острой фокусировки лазерных пучков с круговой поляризацией, в том числе пучков с фазовой сингулярностью, возможно использование отдельного кремниевого цилиндра с субволновым радиусом.

Наименьший размер фокального пятна Гауссова пучка с круговой поляризацией достигается при радиусе цилиндра 1,25λ. В этом случае обеспечивается фокусировка в круглое световое пятно, состоящее из поперечных компонент электрического поля. Минимальный размер светового пятна по уровню полуспада интенсивности FWHM=0,25λ, что лучше, чем цилиндр, демонстрируемый в [4] (0,36λ).

Наименьший размер фокального пятна для моды Гаусса–Лагерра (0,1) вне элемента достигается при радиусе цилиндра λ. Численно показано, что рассматриваемый кремниевый цилиндр, освещённый лазерным пучком с вихревой фазовой сингулярностью первого порядка, формирует световое пятно, центральная часть которого содержит продольную компоненту электрического поля (минимальный размер FWHM z = 0,26λ). Общая интенсивность светового пятна содержит поперечно-поляризованные боковые лепестки, что уширяет размер пятна до FWHM=0,29λ.

Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-19-00114).