Численный анализ влияния испарения и диффузии влаги на тепловые потери теплопроводов, работающих в условиях увлажнения изоляции

Известно, что 40 % тепловых сетей России требуют ремонта, 15 % – находятся в аварийном состоянии, а тепловые потери в сетях превышают 16 % годового расхода топлива на теплоснабжение [1]. При этом одним из главных факторов, приводящих к сверхнормативным тепловым потерям, является эксплуатация теплопроводов в условиях увлажнения изоляции [2–4].

В настоящее время выполнен анализ механизмов влагопереноса в увлажненной изоляции теплопроводов [2], проведены исследования нестационарности процессов тепломассопереноса в увлажненной изоляции [3] и экспериментальное определение [4] тепловых потерь теплопроводов в условиях затопления каналов тепловых сетей. При этом в [2–4] не учитывается влияние фазовых переходов в структуре пористого слоя тепловой изоляции на интенсификацию тепловых потерь рассматриваемых объектов.

Целью данной работы является математическое моделирование тепловых режимов и численный анализ тепловых потерь теплопроводов в условиях увлажнения тепловой изоляции с учетом испарения влаги на границе раздела «стенка трубы – слой изоляции» и диффузии образовавшегося пара к внешней поверхности изоляционного слоя.

Постановка задачи

Рассматривается широко распространенная в настоящее время конфигурация теплопровода [5], уложенного в одноячейковый подземный железобетонный канал. Предполагается, что теплопровод эксплуатируется в условиях затопления канала тепловой сети, что соответствует максимальному увлажнению изоляции [3]. Начальные значения температур и влажности в рассматриваемой области решения (рис. 1) имеют постоянные значения. В момент времени, отличный от нуля, на внутренней поверхности трубы R 1 (рис. 1) устанавливается температура, равная температуре теплоносителя, а на границе раздела «стенка трубы – слой тепловой изоляции» R ₂ начинается испарение влаги. Образующийся пар диффундирует через слой увлажненной изоляции в направлении к внешней поверхности R ₃. Следствием наличия в пористой структуре тепловой изоляции влаги и пара является изменение эффективной теплопроводности теплоизоляционного слоя, а наличие потока массы на внешней поверхности теплоизоляции приводит к изменению механизмов тепломассообмена теплопровода с внешней средой.

С учетом рассматриваемых факторов анализ тепловых потерь сводится к совместному решению нестационарной нелинейной задачи теплопроводности для двухслойного полого цилиндра «стенка трубы – слой увлажненной теплоизоляции» и задачи диффузии пара в слое увлажненной изоляции. Для задачи теплопроводности на внутренней поверхности трубы R 1 выставляется граничное условие первого рода, а на внешней поверхности изоляции R ₃ - граничные условия третьего рода (рис. 1). На границе раздела R ₂ «стенка трубы - слой увлажненной изоляции» учтено наличие испарения влаги. Для задачи диффузии на границе R ₂ задается плотность потока массы, а на границе R 3 – условия массообмена рассматриваемой системы (рис. 1) с окружающей средой.

Задача решалась с учетом следующих основных допущений:

• 1.    На границе раздела «стенка трубы - слой увлажненной изоляции» выполняются условия идеального теплового контакта.

• 2.    Теплофизические характеристики материалов и веществ являются постоянными и известными величинами. Диапазон изменения параметров, влияющих на теплофизические характеристики, в рассматриваемой задаче невелик [6], а следовательно, изменением свойств можно пренебречь.

• 3.    Потери тепла не влияют на температуру внутренней поверхности изоляции. Считается, что теплоноситель в трубе интенсивно перемешивается и движется со скоростью, достаточной для поддержания постоянной температуры в рассматриваемом сечении.

• 4.    Не рассматривается теплоперенос во внешней среде и теплоносителе в трубе (рис. 1).

• 5.    Теплота в стенке трубы и слое изоляции передается только теплопроводностью (рис. 1).

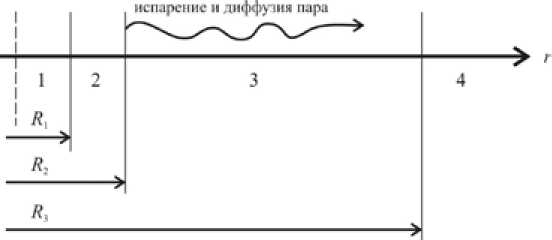
Рис. 1. Схематическое изображение области решения: 1 – теплоноситель; 2 – стенка трубы; 3 – слой изоляции; 4 – окружающая среда

Принятые допущения не накладывают принципиальных ограничений на общность постановки задачи и отражают достаточно реальный режим работы теплопровода в условиях увлажнения изоляции.

Математическая модель

Задача решена в цилиндрической системе координат, начало которой связано с осью симметрии трубы. Математическая постановка задачи имеет вид т > 0, R < r < R2; c2Р2 ^T = ^2 t^T + -^T);                         (1)

Вт      I d r ² r d r )

^т >  0, R 2 <  r <  R 3 ; c f ( ^т , r ) p ef ( ^т , r )     = ^ ef ^{( т} , ^r )^ r ₂+ - _d J ;            ⁽²⁾

т = 0, R 1 <  r <  R 3 ; T2 = T 3 = T 0 = const;	(3)
т >  0 , r = R, ; T = T = const; ,     12 in	(4)
ВТ    ВТ т >  0 , r = R 2 ; X 2 T = Xef -T - jQ ; T 2 = T 3 ; r         r	(5)
т > 0, r = R 3 ;  - x ef ( т , R 3 )5 T = « ( T 3 - T x ) ; ef          d r               ex	(6)
0 R       R    d C st    d [ d 2 C st   1 d C st)	(7)
T = 0 , R 2 <  r <  R 3 ; C st = C 0 = cons t;	(8)
T >  0 r _ R. - D ( T R \d CsL = • - ,        2’        3 Pe , 2 5 r	(9)
T >  0, r _ R 3 ;  - D 3 д-^ _ в ( C st - C x ) . d r	(10)

Обозначения: T - температура, К; т - время, с; r - координата, м; R - граница области расчета, м; λ – коэффициент теплопроводности, Вт/(м∙К); ρ – плотность, кг/м³; c – теплоемкость, Дж/(кг-К); Q - теплота фазового перехода, Дж/кг; j - плотность потока массы, кг/(м²^с); а - коэффициент теплоотдачи, Вт/(м²^К); D - коэффициент диффузии, м²/с; С - относительная объемная концентрация; β – коэффициент массоотдачи, м/с.

Индексы: 1, 2, 3 – номера границ областей расчета; 0 – начальный момент времени; ef – эффективный; in – внутренний; ex – наружный; st – пар.

Плотность потока массы при испарении влаги определялась из соотношения [7]

j =

a (Ps - Pp )

12nRK ,      " ’

V ^ T R 2)

где a - коэффициент аккомодации; P s - давление насыщения, Па; P p - парциальное давление испаряющейся компоненты, Па; R_g – газовая постоянная, Дж/(кмоль∙К); М – молекулярная масса паров, кг/моль.

Коэффициент аккомодации вычислялся по формуле [8]

0.059

.

^а = р 05 ^s

Парциальное давление испаряющейся компоненты в выражении (11) вычислялось методом

Риделя–Планка–Миллера [9]. Теплоту парообразования находили по формуле [10]

Q = 2500.64 - 2.369 T ( т ,R 2 ).

Теплофизические свойства слоя тепловой изоляции определялись с учетом объемных долей каждой компоненты [11]. Например, эффективный коэффициент теплопроводности вычисляется из соотношения

Л/ Л С3 + КС + К Cst при условии, что С3 + Cw + Cst = 1; Cw + Cst = f, где f – открытая пористость, Cw – относительная объемная концентрация воды.

Коэффициент массоотдачи в определялся на основании метода единого описания конвективного тепломассопереноса из выражения [12]

в =

а

— cst Pst

Метод решения и исходные данные

Задача амю) решена методом конечных разностей [13] с использованием неявной четырехточечной разностной схемы. Разностные аналоги исходной системы уравнений решены методами «прогонки» и итераций [13]. Особенность решения задачи ан1о) состояла в разрыве значений теплофизических свойств на границе раздела «стенка трубы – слой увлажненной изоляции» и наличии нелинейного члена в граничном условии (5).

Численный анализ проводился для трубы с диаметром условного прохода 600 мм, изготовленной из стали 10 (толщина 9 мм) и тепловой изоляции из минеральной ваты (толщина 70 мм). Значение температуры в рассматриваемой области решения в начальный момент времени принималось равным Т 0 =298 К. Температура внутренней поверхности трубы принималась равной Т in =338; 363; 383 К и соответствовала среднегодовым температурам теплоносителей в подающих трубопроводах тепловых сетей [14]. Температура окружающей трубопровод среды составляла Т ex =298 К. Коэффициент теплоотдачи от поверхности изоляции к внешней среде на – 492 –

Таблица 1. Характеристики минеральной ваты

Характеристика λ3, Вт/(м∙К) c3, кДж/(кг∙К) ρ3, кг/м3 D3, м2/c f Значение 0.059 0.67 206 4.5∙10-7 0.73 основании проведенных ранее исследований [3] принимался равным α = 11 Вт/(м2∙К). Начальные относительные объемные концентрации воды и пара в пористой структуре слоя тепловой изоляции принимались равными Cw=f и Cst=0, а относительная объемная концентрация пара в окружающей среде – Сex=0.

В табл. 1 приведены физические характеристики [6, 15] слоя тепловой изоляции в сухом состоянии, использовавшиеся при проведении численного моделирования.

Результаты исследования

Основные результаты численного моделирования тепловых режимов теплопроводов в условиях увлажнения изоляции с учетом испарения и диффузии влаги приведены в табл. 2 и на рис. 2.

При проведении численных исследований основное внимание уделялось анализу масштабности влияния эффектов испарения воды на внутренней поверхности трубы и диффузии образующегося при этом пара на интенсивность отвода теплоты в окружающую среду.

Обоснованность и достоверность результатов исследований следует из приведенных проверок используемых методов на сходимость и устойчивость решений на множестве сеток при выполнении условий баланса энергии на границах области расчета. Погрешность по балансу энергии во всех вариантах численного анализа не превышала 0,5 %, что можно считать приемлемым при моделировании тепловых режимов теплопроводов в условиях увлажнения изоляции [2, 3].

В табл. 2 представлены численные значения тепловых потерь рассматриваемой системы (рис. 1) в условиях, когда изоляция не увлажнена Q_dry ; изоляция увлажнена Q_wet ; изоляция увлажнена и учитывается испарение влаги на поверхности трубы Q ev ; изоляция увлажнена,

Таблица 2. Результаты численного моделирования

сЗ S S & & X	Т in , К	Q dry , Вт/м	Q wet , Вт/м	Q ev , Вт/м	Q dif , Вт/м	max Сst	OJ d	d	d о?	d	d d	d	OJ	d
	338	68.1	387.0	430.6	414.4	0.0506	82.4		10.1		3.7		83.6
и У	363	110.7	639.4	845.3	794.5	0.0935	82.7		24.3		6.0		86.1
сЗ со	383	144.7	842.6	1309.1	1202.5	0.1112	82.8		35.6		8.1		88.0

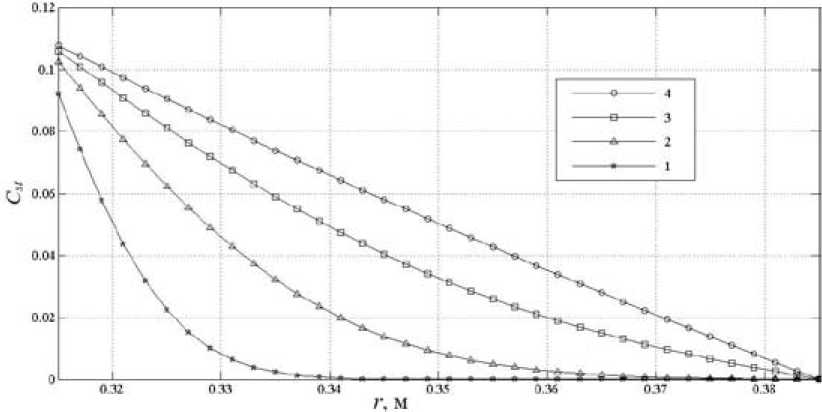
Рис. 2. Распределения относительных объемных концентраций пара по толщине слоя изоляции: 1 – 0,1∙103 c.; 2 – 0,5∙103 с.; 3 – 1,5∙103 с.; 4 – 5∙103 с учитывается испарение и диффузия пара Qdif, а также сопоставление этих величин между собой.

Результаты численного моделирования, приведенные в табл. 2, свидетельствуют об ожидаемом росте тепловых потерь теплопровода с увеличением температуры внутренней поверхности Т п . .

Данные табл. 2 позволяют сделать следующие выводы:

• •    тепловые потери теплопроводов в условиях увлажнения изоляции без учета эффекта испарения ( Q wet ) возрастают на величину около 80 % по сравнению с тепловыми потерями теплопровода, имеющего сухую изоляцию ( Q_dry ) при рассматриваемых в данной работе значениях определяющих параметров (температура, толщина и вид тепловой изоляции);

• •    вклад эффекта испарения влаги на поверхности трубы (рис. 1) в тепловые потери теплопроводов, работающих в условиях увлажнения изоляции, составляет от 10,1 до 35,6 %, что свидетельствует о необходимости учета наличия испарения при проведении численного анализа тепловых режимов теплопроводов, работающих с увлажненной изоляцией.

Учет наличия паровой компоненты в структуре увлажненного слоя тепловой изоляции теплопроводов приводит к снижению эффективной теплопроводности (из-за сравнительно невысоких теплофизических характеристик водяного пара [6]) и, соответственно, к уменьшению общего уровня тепловых потерь. Понижение уровня тепловых потерь составляет до 8,1 % (табл. 2).

Снижение уровня тепловых потерь теплопроводов в условиях увлажнения изоляции с учетом диффузии испаряющейся компоненты ограничено значениями Cst. Максимальные значения относительной объемной концентрации пара в пористой структуре слоя тепловой – 494 – изоляции Сsmt ax приведены табл. 2. Значения Cst сравнительно невелики, однако позволяют заметно уточнить масштабы тепловых потерь теплопроводов в условиях увлажнения изоляции.

На рис. 2 в качестве примера изображены распределения относительных объемных концентраций пара по толщине слоя изоляции в различные моменты времени при Т_in =383 К.

Анализ нестационарности процессов тепломассопереноса для рассматриваемой задачи свидетельствует о том, что время выхода на стационарный режим составляет 2^10 4 с, а для задачи диффузии – 5∙10³ с, что хорошо согласуется с результатами исследований [3].

Результаты численного анализа, приведенные на рис. 2, говорят о том, что выход процесса диффузии пара на стационарный режим произойдет сравнительно быстро, в течение 1,5 ч, что объясняется достаточно высоким значением коэффициента диффузии минеральной ваты (табл. 1). Из анализа рис. 2 видно, что процесс диффузии пара в увлажненной тепловой изоляции теплопроводов является нестационарным, а сопоставление результатов моделирования (рис. 2) с известными данными по диффузии воды и пара в промышленной изоляции [16] свидетельствует об их хорошем качественном согласовании.

Анализ результатов численного моделирования (рис. 2) позволяет сделать вывод о том, что в рамках рассматриваемой задачи нестационарными процессами тепломассопереноса вследствие их малой продолжительности можно пренебречь.

Заключение

На базе совместного решения задач теплопроводности и диффузии проведены моделирование тепловых режимов и анализ тепловых потерь теплопроводов в условиях увлажнения изоляции.

Установлено, что в рассматриваемых условиях тепловые потери теплопровода увеличиваются на 83,6– 88,0 %.

Показано, что нестационарностью процессов тепломассопереноса в увлажненной тепловой изоляции теплопроводов можно обоснованно пренебречь.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 12-08-00201-а и гранта Президента РФ № МК-1652.2013.8.