Численный анализ влияния расстройки параметров на вынужденные колебания системы диск-лопатки турбомашин на основе модели уменьшенного порядка

При изучении колебаний роторов турбомашин известно, что у реальных конструкций при их изготовлении или эксплуатации всегда возникают случайные отклонения между лопатками (по массе, модулю…). Эти отклонения называются расстройкой. Расстройка сильно воздействует на отклик вынужденных колебаний. В зависимости от рабочих условий и уровня расстройки ограничение энергии на несколько лопаток может привести к повышению максимальных амплитуд и напряжений лопаток. Анализ влияния расстройки на вынужденные колебания показан в нескольких работах. В таблице 1 [5, 6, 8, 9] представлен максимальный коэффициент увеличения амплитуды колебаний.

Таблица 1

Год	Автор	Число лопаток N	максимальный отклик с расстройкой отклик без расстройки
1976	Whitehead [ 9 ]	24	1 f 1 + \ N" 1 = 2,23 2 ( V2J
1976	Ewins [ 5 ]	24	1,21
1975	El-Bayoumy and Srinivasan [ 6 ]	24	1,20
1984	Macbain and Whaley [ 8 ]	-	1,20

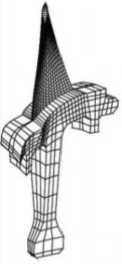
Авторы применяли статистический анализ, чтобы исследовать вынужденные колебания рабочих колес с расстройкой. Но этот метод сложно использовать для конечных элементов системы лопаток (рис. 1а).

В статье представлена методика расчета модели уменьшенного порядка (МУП) для анализа рабочих колес с расстройкой на основе одного сектора методом конечных элементов

(МКЭ) (рис. 1б).

а

б

Рис. 1. Модель конечных элементов рабочих колес: а - полный диск; б - один типичный сектор

Реализация расстройки

Расстройка моделируется путем изменения жесткостей каждой лопатки. Когда матрица жесткости каждой консольной лопатки разлагается на диагональную форму K b , тогда расстройка жесткости каждой консольной лопатки A K b вводится как [ 3 ]

AKb = Bdiag n = 1,..., N

diag A fnk к=1,..., mb

^Kb ^,

где Bdiag - блочно-диагональная матрица; diag - диагональная матрица; mb - число форм n=1,..., N                                                                           к=1,..., mb колебаний консольной лопатки; N - число лопаток; Afk - расстройка параметров, соответствующая k-ной форме колебаний n-ной консольной лопатки, определяемая как ^k >2

A f nk = — - 1 ,

V ^— 7

здесь — n - расстроенная частота к -ной формы колебаний n -ной консольной лопатки и — ^k - настроенная частота k- ной формы n -ной лопатки.

В большинстве опубликованных исследований по расстройке системы диск-лопатки рассмотрены изменения модуля упругости как исходные данные расстроенных лопаток. Если материал каждой лопатки однороден, то расстроенный параметр A f k в уравнении (1) заменяется значением A f n , которое обозначает изменение номинального модуля упругости.

Общая схема моделей уменьшенного порядка

аб

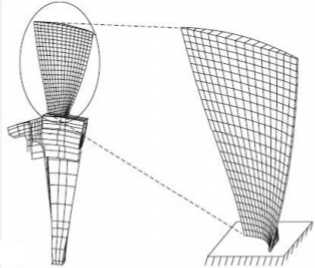
Рис. 2. Компоненты форм одного сектора: а - циклические формы для одного сектора диск-лопатки; б - нормальные формы одной консольной лопатки

Предположим, что степени свободы упорядочены так, чтобы дать блочнодиагональные формы при сборке матриц масс и жесткости всей конструкции. Они представлены в виде [ 3 ]

M =	■ M d 0 "	=	I ® Md    0	, K =	Г K d
	[ 0 M b .		0    I ® M b		L 0

0     I ® K d    0

=

Kb J [ 0    I ® Kb где I - единичная матрица размера N; N - число

секторов, M d , K_d - матрицы масс и

жесткости одного сектора диска; Mb, Kb - матрицы масс и жесткости одной лопатки, символ 0 обозначает оператор Кронекера, определенный в приложении А.

На рисунке 2 изображены два основных компонента форм колебаний для модели конечных элементов одного сектора диск-лопатки. Первая часть включает в себя формы колебаний одной лопатки, защемленной между диском и лопаткой (рис. 2б). Для колес без полки модальная матрица ab N идентичных лопаток является блочно-диагональной и собрана как I ®5b, где 5b - форма колебаний одной консольной лопатки. Вторая часть представляет собой формы колебаний диска, которые являются циклическими формами полной сборки, где к диску присоединены безмассовые лопатки (рис. 2а). Часть форм колебаний диска с лопаткой принадлежит степеням свободы лопатки и обозначается 5d, а часть диска - Sd. После совмещения двух частей компонентов форм колебаний получим перемещения всей структуры в виде [4]

xd xb

5d     Го a +

5 ^d       5 b

b ,

TTTT a0 a1 ... aP I ; an - один вектор обобщенных координат, соответствующих n узловым диаметрам диска; P -максимальное число гармоник или максимальное число узловых диаметров; b - вектор обобщенных координат для всех N лопаток и b = [bT bT... bTN J , где bi - вектор обобщенных координат i-ной лопатки.

Кинетическая энергия системы может быть записана как [ 7 ]

P    PP   PP t=7£ a1 Tan+7 b Tb+b Tab Mb £ 8aa n+- I£ a Tad I Mb^b+- £( a Tad Mb £( 8^ .). (5)

2 n=0         2     =             n 0 =       2 V n 0 = У           =2 n 0

Аналогично энергия деформации системы может быть выражена как

PP

U = 7 £ 4KA + 7 b T a b K b a b b + - b^T 5 b K b £ S aa.

2 n=0             2                  2

PPP

+ ⁷1 У a^T5^d \k ,5^bb + 1У Ta^T5^d Vy(5^da A

2 I n n I b n             ⁿ I b m m J

V n=0        У = 2 n 0

Применяем принцип Гамильтона t2t2

J [ dU - dT ] dt = J dW внеш dt , t ₁ t ₁

где внешняя работа определена как j dWBHemdt = j d [5da + 5bbJT Fdt JdaTadTFdt + j dbTebFdt, t1t1                                                              t1t1

а F - соответственно вектор вынужденной силы степеней свобод всех лопаток при сборке. Из выражений (3 - 8) имеем уравнение в виде матрицы

Id + ^TMb^ [ ^bMb^ T  00 8 Mb8  a                        a ;      b + 0 diag [2^k]0^€b  j, Ib ][ ] [      k=1,..., mjL     J          ][ ] dTb                                       () „         K€d         .   8 Kb8   ,   Г a 1   8'F + (1 + y j)    T                       /                   = 8b Kb8d  Bdiag diag (1 + Af!k) K€b [b]   8^F   , n=1,..., N k=1,..., mb где Id, Kd - соответственно матрицы масс и жесткости диска в размере NmdxNmd, когда все формы с матрицей масс нормированы; md - число форм колебаний диска; Ib, Kb - соответственно матрица масс и жесткости N лопаток в размере NmbxNmb, когда все формы с матрицей масс нормированы; ^ - коэффициент вязкого демпфирования; у - коэффициент демпфирования структуры.

Определение циклических форм колебаний [3, 7]

Матрица, представляющая собой циклические формы колебаний, определена как 3 d = ( F 0 I ) 3 ^d ,                                           (10)

где F - реальная матрица Фурье (см. приложение Б); I - единичная матрица размера N; 3^d - форма колебаний одного сектора в циклических координатах, имеющая блочнодиагональную структуру и определена как

3 ^d = Bdiag 9 ^d ,                                           (11)

k=0,..., P где 3k = 3tc + J9ds - форма колебаний одного сектора, соответствующая k узловых диаметров; 3d c, 3ds - соответственно реальная и мнимая часть 3d и j = V-1.

Из выражений (10) и (11) можно получить форму колебаний в циклических координатах как

3d =[f,030 fc031d,+f s031ds,..., "ft0atc + "ft0C,- fN/203/2]■(12)

Определение возбуждающей силы [7]

Возбуждающие силы - гармонические функции времени, отличающиеся фазой между секторами. Фаза i -ной лопатки определена как

Ф,- ^N" 1) •        О' = U,N)'(13)

где C - порядок энергии возбуждений.

Вектор внешней возбуждающей силы представлен в виде

F = {fe^1 =^2 ... fjN }T NeCec+1 0 f,(14)

где e_{c + 1} - (С+1)-й столбец матрицы Фурье в приложении Б; f - вектор вынужденной силы одной лопатки.

Из выражений (9) и (14) имеем

F = {FT: Ft} = {0... 0 FC 0...0 M Ft}T,(15)

( f 0 ® S ) ( ■ + 1 ® f )

( f c ® S d ₌ + f ‘ ® S i /, ) ( e_c + i ® f )