Численный метод для модели Эйлера движения переохлажденных капель в условиях обледенения

Моделирование нарастания льда на поверхности тела изучали в разных исследовательских центрах разных стран, например, в NASA (США), ONERA (Франция), DRA (Великобритания) [1]. Процесс моделирования нарастания льда можно разбить на три этапа:

• •    В условиях обледенения, объёмная доля переохлажденных капель очень мала, поэтому можно рассмотреть поле воздуха, и поле водности отдельно, пренебрегая влиянием капель на. течение воздуха. На первом этапе осуществляется моделирование обтекания летательного аппарата, (в дальнейшем - ЛА) сухим воздухом. Движение воздуха, описывается системой уравнений Рейнольдса. Первый шаг является достаточно стандартным и не требует дополнительного описания.

• •    На втором этапе проводится моделирование движения переохлажденных капель в локальном поле газодинамических параметров, рассчитанном на. первом этапе.

• •    На третьем этапе проводится моделирование термодинамического процесса нарастания льда на поверхности ЛА. Так как наросший лед изменяет геометрию ЛА, цикл расчета может повторяться.

2.    Модель Эйлера движения капель

В данной работе рассматривается вторая задача. При моделировании движения капель применяется два подхода. В программе LEWICE [2] и IGLOO2D (ONERA) [3] применяется подход Лагранжа. При таком подходе непосредственно рассчитывается движение капель. В программе FENSAP-ICE [4] используется подход Эйлера, рассматривается плотность капель и уравнения (будем назвать их уравнения водности^ напоминают систему уравнений Эйлера. С практической точки зрения, второй подход имеет существенные преимущества. Прежде всего это совместимость с солвером движения воздуха, в котором обычно используется подход Эйлера. Использование одних и тех же расчетных сеток на первых двух этапах существенно сокращает время подготовки расчета, упрощает портирование данных при переходе ко второму этапу, позволяет упростить расчет сложных геометрий. Кроме того, подход Эйлера требует существенно меньших затрат вычислительных ресурсов, особенно для больших ЗП-задач.

Систему уравнений водности можно рассматривать как уравнения газа без давления. Система уравнений движения капель является слабо гиперболической, что может приводить к проблемам с устойчивостью метода решения. Существуют походы, основанные на регуляризации системы уравнений водности путем добавления в нее фиктивных членов [5,6]. В данной работе представлен метод решения оригинальной модели Эйлера движения капель и показано, что предлагаемый метод достаточно устойчив и эффективен.

Основные принципы описания движения переохлажденных капель с подходом Эйлера изложены в работе [8]. По законам сохранения массы и импульса формируется система уравнений водности:

^дР + ^d(p^u j ) = 0

dt дх j ’

^ + dCpuiuj) = FD1 + ғОв„ dt dxj где p = pwа - водность или абсолютная влажность, а — обёмная доля капель, pw — плотность воды, Ui — скороеть капли, Fai ~ сила сопротивления от потока воздуха, Fg ві. сила тяжести и плавучести:

0.75C_B Re _a p                  ^p

Fa =-------,2----PVVai - Ui), FGBi = (1--)pgi, pwd                           pw где p — молекулярная вязкость. uai — г-компонента скорости воздуха, d — средний диаметр капли. Cd ~ коэффициент сопротивления. pa — плотноеть воздуха, gi— ускорение свободного падения.

Число Re a вычисляется по следующей формуле:

Re = ^ к

Р

- ^U | .

Для определения Cd используем эмпирическую формулу [8]:

( ^(1 + 0.15Rea. 6 ⁸⁷, Re a <  1000, t 0.4, Re a >= 1000.

Для определения свойств системы уравнений водности рассмотрим её двумерный ана- гог:

dU дҒ ЭН dt дх ду

где

( р А / pit \        / pv \        /     0

pu I , Г = I pu² I , Н = I puv I ,Q = I F _D x + F _GB x pv)      \puv/      \pv²/       FDr+ + F _G By

Перепишем систему: эи эи эи_

Hi + Jx dx + Jy дХ = Q, т дғ т дн где Jx = "g^, Jy = "g^J ~ матрицы Якооиаи. Для лтооого единичного вектора 11 = (пх,ПуД . рассмотрим матрицу А = JxHx + Jyny;

А =

—и(Ү.п)

—v(V.n)

Пх           Hy ипх + (Үлі)     UHy vnx     VHy+ (Ү.іД

Она имеет три одинаковых собственных значений A 1 = A 2 = A 3 = V.n. Система (2) является слабо гиперболической.

3.    Численный метод

Численный метод строится в рамках конечно-объемного подхода, конкретнное описание которого можно найти во многих источниках, например [12]. Для простоты рассмотрим фиксированный объем V в одномерном потоке, кото рому присваивается номер (г). Численная схема для системы водности будет иметь вид п

Ui+1 = U — V №+1/2 — F.-1/2] + TnQi, где тп — шаг по времени, Д±1/2 — потоки сквозь грани ячейки. Здача определения заначе-нии этих потоков называется задачей Римана о распаде произвольного разрыва. Для решении задачи Римана используем метод типа Годунова для уравнений газодинамики [7,11]. Конкретно, рассмотрим локальную одномерную задачу Римана:

U (x,t = 0) = ^

^U L , ^x< ^X i +1 / 2 , Ur, X >  Xi +1 / 2 .

Поскольку система (2) имеет только одну характеристику (три характеристики совпадают), возможные конфигурации постановки задачи показаны на рис. 1.

По положению левой и правой характеристик мы предлагаем следующую схему для определения решения:

ul >  ur :

ul :

^Ui +1 / 2 = I

^Ui +1 / 2 = *

Ul, ос ли ( plul + prur ) >  0,

Ur, лргой случай,

Ul, если ul >  0,

Обратим внимание на случай столкновения потоков. В таком случае, критерием для выбора решения является сумма импульсов потоков. Если эта сумма больше нуля, то по закону сохранения импульса, импульс образующего потока после удара также больше нуля, из чего следует, что его характеристика направлена вправо. Поэтому мы возмьем Ui+1/2 = Ul-

Для вычисления потока сквозь грани ячейки используется формула

^Fi +1 / 2 = ^{F (U} i +1 / 2 )•

В данной работе, рассмотрим два типа схем: схема первого порядка Годунова (Godunov), схема второго порядка TVD (Kolgan, vanLeer). Сравнение этих схем будет представлено в следующей главе.

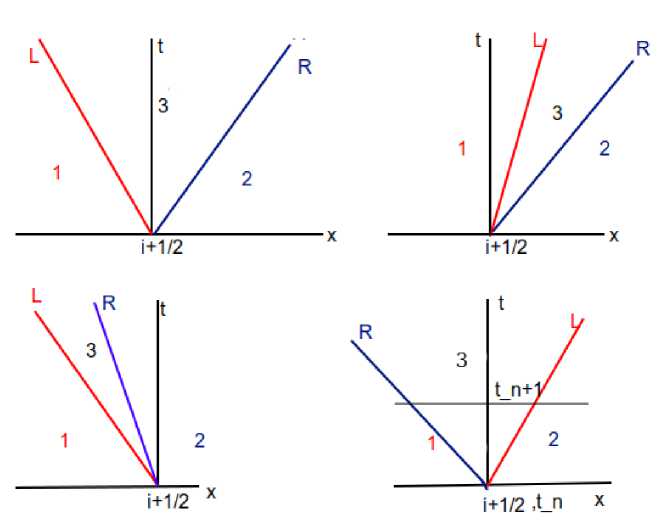
Рис. 1. Постановка, задачи Римана.

4.    Модификации модели Эйлера движения капель и их численный метод

Система, уравнений (1) очень похожа, на. систему уравнений движения невязкого газа. Эйлера, если не учитывается однин аспект: у неё нет статического давления. Как показано выше, она. не является гиперболической.

С попыткой превратить систему (1) в гиперболическую обычно дабавляется некое «давление» в левой [6] или в обеих [5] частях уравнений. Это давление определяется по формуле Pd = Cp^k , где С - некоторый коэффицент, к = 1.0, 2.0, ... В этой статье используется формулу pd = Cp с коэффициентом порядка C ~ 0.001, как предполагается в работе [6]. Это давление называется давлением частиц. Оно прямо пропорционально водности. В итоге, мы получим ещё две модификации модели движения капель:

' Эр + Ә(ри , ) = ₀ dt dx j ’

Ә^ г) , Э⁽ри р и , + p d ^ ij )   _{r r}

1 = ^ Di ^{+ F} GBi ot          ox j

' dp + d (pv j ) = 0

• _< dt      dx j        ,

  
  

* d(pu i ) d(pu i H j ⁺ p d ^ ij ) = эр д _F

_ dt ⁺ dx j          ^{9x 4 + Di +}

Эти системы гиперболические, для решения их задачи Римана, можно использовать метод Роу [7]. Сравнение метода. Годунова, для оригинальной системы и метода. Роу для модификаций будет представлено в следующей главе.

С давлением частиц p d = Cp, эти системы похожи на систему уравнений изотермического газа [7]:

U + f (и )х = 0, где в одномерном случае

и =

f p),F =f 2

V pu        pu ²

pu

+ pa2

,

а - ненулевая константная скорость распространения звука. Для Якоби, пусть U 1 = p,U 2 = ри

определения матрицы

Следовательно

A(U )

дҒ ди

^U =(U 2) '^Ғ = (и 2 /„1"+ а 2 и,) •

0           1    =

— (U 2 /U 1 )² + а² 2 u 2 /ui_

а2

-

и2

2и "

Матрица Якоби А имеет два собственных числа

Ai = и — а, А2 = и + а и два правые собственных вектора

К = ( 1 ) , K2 = ( 1   • и — а у       у и + а}

Соответственно, в приближении Роу имеем:

U +1 / 2 = 2( Ul + Ur ) — 2R₈ign^)R ^-1 (U R

-

Ul ) ,

где R — матрица, столбцами которой являются собственные векторы, Л — диагональная матрица, диагональ которой состоит из собственных чисел. Тогда, поток сквозь грани ячейки определяется по формуле

^Ғ і +1 / 2 = ^{Ғ (и} { +1 / 2)

ИЛИ

^Ғ і +1 / 2 = 2^(F L ^{+ F}R^{) —} 2^Ғ|Л|Ғ 1 ^(UR ^{— U} L )-

По постановке Роу величина и, появляющаяся в R, Л, вычисляется следующей формулой:

_и = ul Vpl + ur ypR

P R

•

Однако при решении реальных задач движения переохлажденных капель в расчете может появляться зона, куда капли не попадают. В этой зоне нет капель, то есть р = 0. В таком случае, чтобы избежать ошибки деления на ноль, для вычисления средней скорости Роу используется формула:

_и = ul + U R

•

5.    Численные результаты5.1.    Безразмерные одномерные задачи

Рассмотрим простейший вид системы (1) — безразмерные одномерные уравнения движений капель:

да   д(аи) _

. дt дт '

д (аи)    д (аи2')        ,        .

⁺ д =     ■ ^{— и)}'

где а — объёмная доля, д — коэффициент сопротивления. и _а — скорость воздуха.

Постановка задачи Римана:

I, ж < 0, ), ж > 0.

(а,«)(х,0) = { (“Д)

( (“г, "г,

Точное решение этой задачи представлено в статье [9]. Это решение — либо дельта-шок, либо вакуум.

В случае дельта-шока "/ > "г

(“/, u l(ж,t)), ж < ^(t),

(“, ")(ж, t)

< (ш(^5(ж - £(<)),  ^(t), где

(Ю)

(И)

„(t) = v- " г ) ₍₁ _ .-„,_

д

Л») =  + / ^ + , .„г - х .-„_ у V “/ + V“r      /

^(t) — дельта функция,

^(t) = /0 ^ds, иі(ж, t) = "a + ("/ — "а)е^, иг(ж, t) = "а + ("г — "а)е^.

В случае вакуума "/ < "г

(а, ")(ж, t) = <

(а / , иф жД)), ж <  X i (t), (0,"(ж,t)), Xi(t) < ж < ^(t), (“г, u г(ж,t)), ж>Х2^),

где	, ^(ж — "at) "(ж,t) = "a +e#zt — 1 , Xi(t)= "at + ( " a —    • ' " 1) ,                             (12) ^. X2(t)= "at + ( " а - " г ) <е " — 11 . ^

Конкретные постановки задач показаны в табл. 1. Другие параметры расчетов пред-

ставлены ниже:

^ = 0.2, "а = 1.0, Аж = 10-2, At = 10-3, t = 1.0.

Таблица!

Одномерные задачи

	“/	"/	“г	"г
Дельта — шок	0.008	1.5	0.003	0.5
Вакуум	0.008	0.5	0.003	1.5

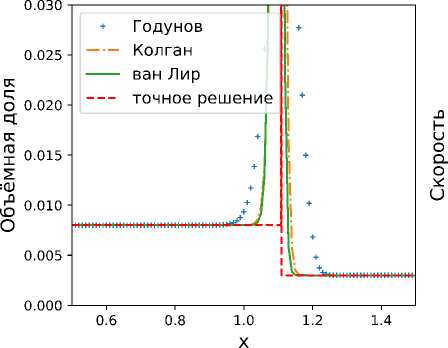
Первая задача представляет случай образования дельта-шока при столкновении потоков. Вторая задача — это случай, когда два потока отделяются друг от дргуга, вследствие образуется вакуум.

Сравнение реконструкций Годунова, Колгана и ван Лира

Полученные результаты в момент времени t = 1 представлены на рис. 2 и 3. Видно, что разработаный метод дает приемлемые результаты, при этом схема ван Лира дает более точные результаты чем схемы Колгана и Годунова.

0.8

1.4

1.2

1.0

0.6

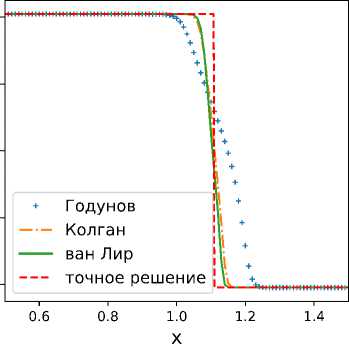
Рис. 2. Образование дельта-шока.

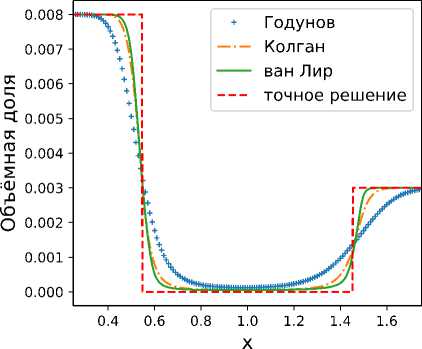
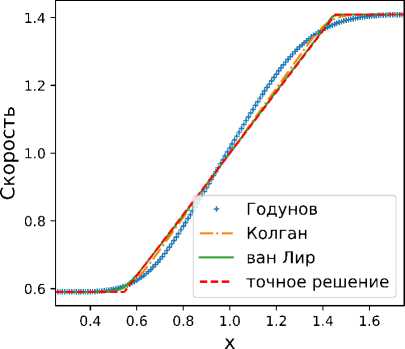
Рис. 3. Образование вакуума.

• 5.2.    Двумерные задачи

Задача свободного падения капли

Рассмотрим втекание капель в расчетную область под действием силы тяжести, пренебрегая силой аэродинамического сопротивления в неподвижным воздухе. Начальные параметры расчёта:

d = 16 місм, Vd = (10.0, 0.0) м/с, р = 0.01 I //з i³, д = 9.8 м/сЛ

На рис. 4 представлено поле плотности капель и результат сравнения траектории потока, с траекторией тела, брошенного горизонтально со скоростью п: ж = nt,у = у о + gt²/2. Результат показывает совпадение этих траекторий. Это значит, что гравитационный член в уравнении движения капли правильно работает.

Влияние ветра

Далее рассмотрим, как ведет себя поток капель в гравитационном поле, когда ветер дует вверх. Начальные параметры:

d = 1, 6 мм, Vd = (80.0, 0.0) м/с, р = 0.55 г/м³, д = 9.8 м/с², Р = (0.0, 5.0) м/с.

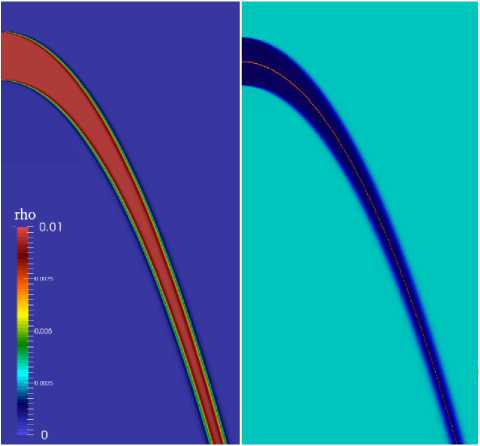
Рис. 4. Свободное падение потока, капель

Здесь мы увидим накопление капель из-за. противодействия на. них силы ветра, и силы гравитации (рис. 5). Когда, концентрация капель достаточна, большая, они падают вниз (рис. 6).

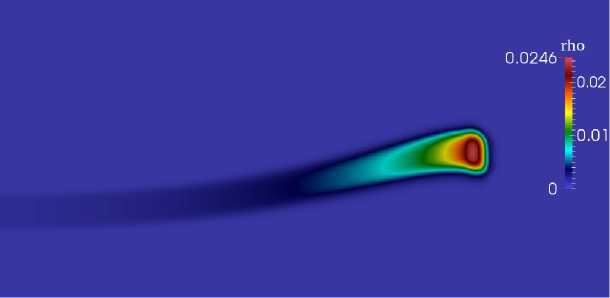
Рис. 5. Поток капель под действием ветра, и гравитации

Рис. 6. Поток капель под действием ветра, и гравитации

Результаты этих двух тестов показывают, что в разработанной программе все силы, действующие на. капли, физичны.

Обтекание цилиндра

Рассмотрим обтекание цилиндра потока капель диаметра d = 20 мкм, водность (LWC) р = 0.54 г/м³. Начальные параметры:

V_a ^ = (90.0,0.0) м/с, р = 100000.0 Па, Т = 268.3 K.

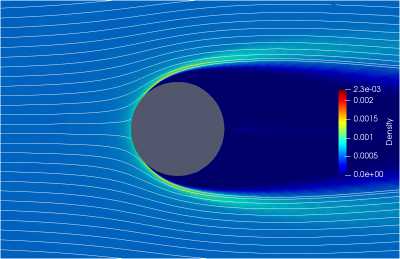
Рис. 7. Поле водности обтекания цилиндра

Для вычисления течения воздуха используется модель турбулентности Спаларта-Алмараса. На рис. 7 представлено поле водности и траектории движения капель. Видно, что поток капель отрывается от поверхности цилиндра, образуется «сухая зона» за ним, в которой водность очень мала.

Дальше проведено сравнение скорости сходимости решения при использовании оригинальной системы уравнений водности (1) методом Годунова, и модифицированных систем (5), (6) методом Роу. Для этого рассматривается коэффициент захвата капель на поверх ности:

Р =

^p w V ^

p^V^

где p_to, Vr,n есть водность и нормальная скорость капель на поверхности, p^,V^ — параметры набегатощего потока капель.

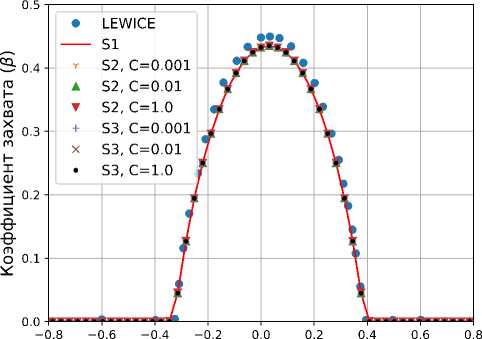
s/c

Рис. 8. Локальный коэффициент захвата

На рис. 8 показано, что численные результаты всех систем уравнений (S1 — система (1), S2 — система (5), S3 — система (6) при коэффициентах давления С = 0.001, С = 0.01, С = 1.0 практически совпадают. Это объясняется тем, что в систему (6) добавление давления частиц в обеих частях устраняет изменения в результате, а в системе (5) это давление маленькое по значению и оно очень слабо влияет на результат. Также видно, что полученные результаты мало отличаются друг от друга и от результата LEWICE [10] — двумерной программы моделирования обледенения в NASA.

Дальше на рис. (9) представлена сходимость суммы коэффициента захвата на всей поверхности цилиндра по числу итерации техники локального шага по времени. Скорости сходимости решений разных методов не сильно отличаются.

1.6 -г

0.0 -_ о

1.4 -

1.2 -

1.0 -

ГО

0.8 -

0.6 -

0.4-

0.2 -

52, С=0.001

52, С=0.01

52, С=1.0

53, С=0.001

53, С=0.01

S3, С=1.0

число итерации

Рис. 9. Сходимость решений по итерации

6.    Заключение

Вычислительные результаты показывают, что разработанный метод типа Годунова, основанный на решении задачи Римана, является достаточно простым и позволяет получать приемлемые результаты при решении системы уравнений водности.

Методы, основанные на искусственном добавлении давления в исходные уравнения водности (1), приводят к незначительному увеличению скорости сходимости решения. При этом, добавление давления в систему и использование метода Роу для модификаций системы (5) и (6) усложняют математическую модель и код солвера. Поэтому автор предлагает использовать разработанный метод типа Годунова для решения оригинальной системы уравнений водности.