Численный метод исследования стационарных режимов в технологических печах

Для высокотемпературного нагрева нефти и нефтепродуктов в процессе их переработки в ректификационных установках применяют трубчатые печи. Печи работают следующим образом [1]: мазут и газ сжигают в горелках, расположенных в камере радиации. Продукты сгорания из камеры радиации поступают в камеру конвекции, затем направляются в газосборник и по дымовой трубе уходят в атмосферу. В камере конвекции расположены конвекционные трубы, воспринимающие тепло при соприкосновении дымовых газов с поверхностью нагрева путем конвекции. Нагреваемый продукт в печи последовательно проходит через конвекционные и радиантные трубы, поглощая тепло. Радиантная поверхность воспринимает большую часть тепла, выделяемого при сгорании топлива (рис. 1).

Горение жидкого топлива всегда протекает в паровой фазе, причем испарение обеспечивается подводом тепла из зоны горения паров. Топливо всегда сжигается в распыленном виде.

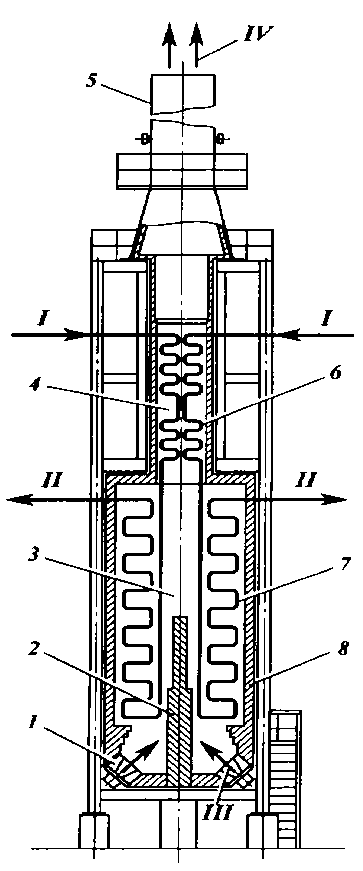
Рис. 1. Схема трубчатой печи: 1 – горелка; 2 – настильная стенка; 3 – камера радиации (топочная камера); 4 – камера конвекции; 5 – дымовая труба; 6 – змеевик конвекционных труб; 7 – змеевик радиантных труб; 8 – футеровка. Потоки: I – вход сырья; II – выход сырья; III – топливо и воздух; IV – дымовые газы

Крайним случаем горения капель является диффузионное горение, когда скорость сгорания паров очень велика по отношению к скорости диффузии паров и окислителя в зоне горения, толщина которой становится исчезающе малой. К такому режиму может приближаться горение сравнительно круглых капель. Диффузионная теория горения развита Г.А. Варшавским [2].

В математических методах анализа процесса горения имеются некоторые расхождения у разных авторов, но для стационарного сферического горения используется единый подход. Для упро-щения анализ проводится при следующих предположениях:

• 1.    Жидкая капля имеет сферическую форму.

• 2.    Влиянием конвекции пренебрегают, пламя рассматривают как сферическую поверхность, концентрическую с каплей.

• 3.    Пламя считают разновидностью диффузионного пламени, которое образуется в результате реакции между парами горючего и воздухом, реагирующими в стехиометрическом соотношении.

• 4.    Рассматривают стационарное состояние при постоянном диаметре капли, хотя реально диаметр жидкой капли уменьшается по мере горения, однако это изменение происходит медленно по сравнению с изменением скорости диффузии и прочими факторами.

• 5.    Температура капли одинакова по всему объему.

• 6.    Давление в течение всего процесса горения считается постоянным.

• 7.    Влияние излучения рассматривают отдельно.

Исходя из законов механики сплошных сред, можно получить следующие уравнения не- стационарного горения:

(

др др ди

7п = -и1й-Р1Й’

дх дх х м_-иТГт'

ди _ ди дТ_п КТ „ др д1 ^и д1 д gi р дГ

дТп           ди

"дМ1-^-

^дТ п . ^хЯ

^U д1 C_vt

-

r^l

С.. 'К(

-

Т п ) + К 1 (Т_С ²

^{- Т} п )’

^д-^Т - _^№д-^Т- + ^К 2 (Т п - Т 1 ) - Q(Т п ,Т 1 )’

дТ2      дТ2

-£- = -w -i^- + К₂ (Тп - Т ² ) - Q(Тп, Т_с ² ).

Здесь x(l,t) - концентрация горючего вещества, p(l,t), u (l,t), T_n(l,t) - плотность, скорость и температура дымовых газов; T c ^(l,t), Fc^(l,t) ^- температура нисходящего и восходящего потоков нагреваемого сырья; t, l - временная и пространственная координаты.

Начальные условия

p ⁽ l,0) = p o ,x ⁽ l,0) = X o ,u ⁽ l,0) = U o ,T_n ⁽ l,0 ⁾ = T_nQ,TKl,0) = 7’_c¹_o,T_c²(Z,0) = T c0 .

Граничные условия

P ( 0, t ) = a , , x ( 0, t ) = a 2 , u (0, t ) = a 3 , T n (0, t ) = a 4 , T_c '( L , t ) = a 5 , T_c 2 (0, t ) = T_c '(0, t ).

Здесь L – длина печи.

Стационарную модель, которая следует из (1), рассмотрим более подробно:

- 9 ^p -p⁹^ = 0. 9l 9l

9x

^-un^- ^-r⁹-^- 9l 9l

X

7 = ⁰ -

^R T9 p

p 9l

= 0,

9u   9 T x Q(T)

(1-^9Ги^ + ^-^ + ^^

9T1

W^r+K2(T„-

-» ^9T- + K 2 (T_n

-T c ¹)-Q(T_n, T c ¹) = 0,

Tc2) - Q(Tn,Tc2) = 0.

Второе, пятое и шестое уравнения содержат пространственные производные только одной неизвестной функции

Приведем первое, третье и четвертое уравнения к виду, содержащему производную только от одной искомой функции dp/dt , du/dl и dT_n/dl . Для этого применим теорию о неявных функциях к системе.

9u

(1 y)T" 91

9p 9u u9l + p9i = 0'

9u   9T RT 9p u^T + R-^ + —^7 = 0'

91      91 p 91

„ 9Ti ₌ 91

— ^_q + ^Q4Tl — K_1№ + T_c² C ^ t C_v ^p

^2т п ) = Ф-

В этом случае где

9p Дг 9u

9й = Т'9й

Д 2 9t

д'

= д'

д =

u RT p 0

p

u

(1 —y)T,

R

RT

^—u3 ^{+ up}_^ ^{— uR(1 —}_Y^^T _a =

—u³ + yRuT_n = u(yRT_n — u²)'

—u

д , = |0

V

^{p u} (1 — ^

^R I= ^R PV' Д 2 = ^-ul

u Rb.

P 0

R

-и

^-Ru V'

Дз —

и

ТТ р о

р 0

и 0 — и²ф.

(1-Y)Tn ф

Таким образом, будем иметь:

Эр Д2      Трф э Д и^- и

Эи Д2        Тиф           Тф(10)

Э1 Д      и ( у ТТ_п - и²)      уТТ_п - и²'

ЭТ_п Д₃       и²фиф

Д                   и       J'1

Тем самым система (4) приведена к следующему виду:

э ^Р^-с^ + пС^^{- к}1⁽т= ^{+ т}=^{- 2Тп)} )

• 91drV

di V ( ^Х П I 5(^тп⁾          , т2 чт»

9Т “(-С^^т^^ ^ 1 ⁽¹ = + ^т = ^- 2 ^т))

• -^ " ------YRT - ц2-------------■

ди₌-«^^ di                yRT -и²

дТ= К2       ,1

Й-»^)"^

дТ=2     К2        ,1

ir--w(Tn-T=)-wQ(Tn-T=).

р (0) = а , , x (0) = а ₂, и (0) = а„ T (0) = а ₄, T ( L ) = а ₅, Т_Е ² (0) = T (0). (12)

На рис. 2-5 изображены результаты расчетов стационарных режимов при различных начальных условиях для плотности p(l), концентрации x(l), скорости u(l) и температуры дымовых газов T_n(l). При этом за начальные условия приняты р(0) =720 кг/м ³ , x(0) =0,47, u(0) =5 м/с, T „ (0) =450 °C, T c (L) =270 °C. Затем начальные данные изменялись с шагом ±5 % при постоянных значениях остальных параметров.

Предлагаемый метод анализа стационарных режимов технологических печей позволяет еще на стации проектирования ректификационных установок обеспечить высокое качество разделения многокомпонентных смесей в нефтепереработке и нефтехимии.

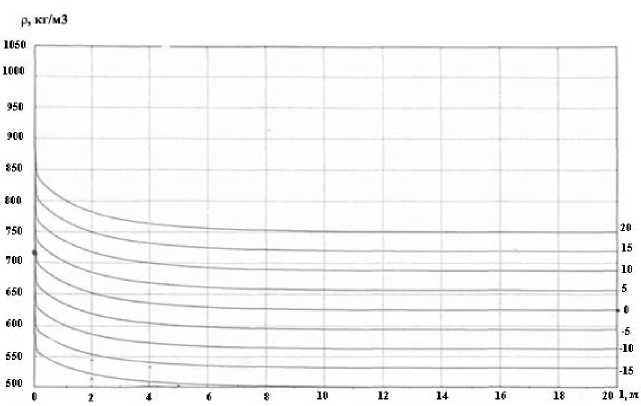
Рис. 2. Графики распределения плотности дымовых газов по длине объекта

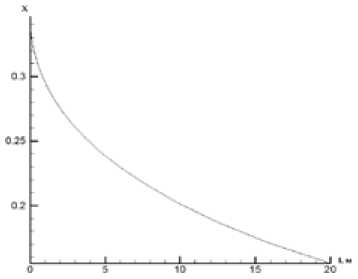
Рис. 3. Графики изменения концентрации по длине объекта

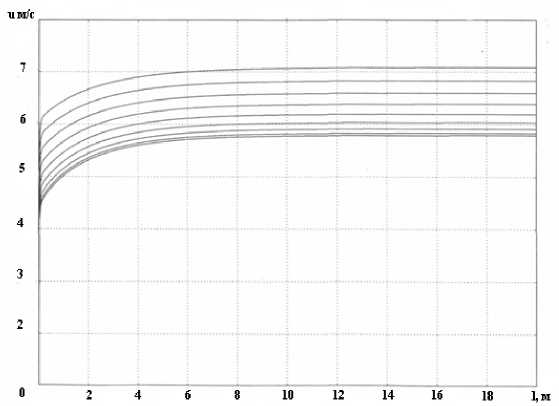
Рис. 4. Графики изменения скорости дымовых газов по длине объекта

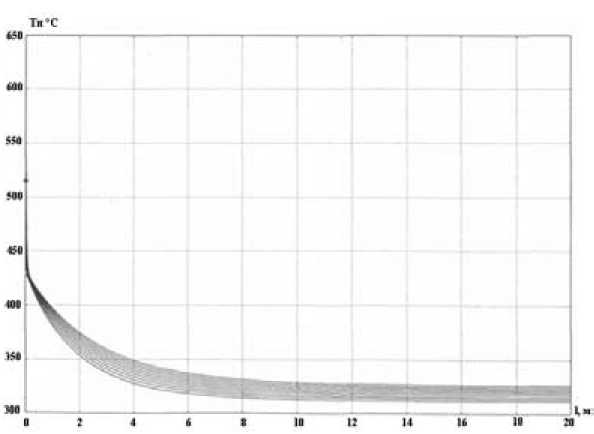
Рис. 5. Графики изменения температуры дымовых газов по длине объекта

In article we propose mathematical models for stationary and dynamic processes of technological furnaces as object with distributed parameters. This mathematical model is based on the laws of conservation of energy, mass and impulse and includes differential equations in private derivatives. Computational investigation of stationary modes of tubular furnaces is conducted. Formulated boundary-value problem for calculation concentration of combustible substance, density, speed, temperature of the flue gas and temperature of the heated raw materials going on division in rectificative column. Results of calculation technological parameters are presented. The proposed method can be used at automation rectificative plant in petroleum-refining and petrochemical industry.