Численный метод порогового разделения секрета над группой точек эллиптической кривой
Автор: Афонин Михаил Сергеевич, Бабенко Михаил Григорьевич, Гладков Андрей Владимирович, Ляхов Павел Алексеевич, Червяков Николай Иванович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 1 т.11, 2013 года.
Бесплатный доступ
В работе представлен способ разделения секрета на базе несовершенной пороговой схемы Миньотта и схемы распределения ключей Месси-Омуры. Объединение пороговой и эллиптической криптографии имеет преимущество в параллельной обработке частей секрета, пролонгации, верификации, изменения числа пользователей и энтропии частей секрета по сравнению с существующими аналогами. Предложенная схема может быть использована для построения систем защищенной передачи, хранения, обработки и презентации данных в компьютерных сетях.
Криптосистема на точках эллиптической кривой, система остаточных классов, схемы разделения секрета
Короткий адрес: https://sciup.org/140191607
IDR: 140191607 | УДК: 621.391
Текст научной статьи Численный метод порогового разделения секрета над группой точек эллиптической кривой
С развитием инфокоммуникационных технологий возникают новые задачи, связанные с защищенным хранением, передачей, обработкой и презентацией данных. При шифровании, позволяющем с обеспечением защиты хранить и передавать информацию, теряется структура данных, что приводит к невозможности обработки данных в зашифрованном виде без предварительного дешифрования и, следовательно, к раскрытию вероятным злоумышленником секрета. Использование протоколов конфиденциальных вычислений требует каналы передачи данных с высокой пропускной способностью. Задержка приема и передачи в компьютерной сети составляет единицы миллисекунд, операция с плавающей точкой занимает несколько наносекунд. Такие задержки неприемлемы для обработки больших объемов данных.
Одним из вариантов решения обозначенных актуальных и перспективных задач защиты информационных технологий выступает распараллеливание обработки на уровне элементарных операций: сложение, вычитание, умножение. В криптографии есть направление, посвященное разделению секрета на части, которое развивает схемы с распределенной обработкой данных. Частным случаем данных схем являются порого- вые схемы разделения секрета, которые делятся на две группы: совершенные и несовершенные. В совершенной схеме энтропия частного секрета равна энтропии разделяемой информации, когда в несовершенной – энтропия частного секрета меньше энтропии общего секрета.
Процесс разделения секрета на практике сопровождается верификацией передаваемых по сети данных, пролонгацией системы защиты посредством обновления секрета или только его частей, изменением числа пользователей. Причем совершенные схемы для решения дополнительных к разделению секрета задач используют алгоритмы ассиметричной криптографии над конечным полем, а несовершенные схемы – свойства алгебраической структуры, над которой построены схема.
Данная особенность привела к следующему предположению: возможна реализация порогового разделения секрета на базе несовершенной схемы с энтропией частного секрета не меньше энтропии общего ключа, обеспеченной алгоритмами ассиметричной криптографии, с сохранением относительно невысокой сложности алгоритмов решения дополнительных задач пороговой системы. Другими словами, использование асимметричной криптографии в совершенных пороговых схемах продиктовано необходимостью расширения функционала системы защиты данных, а в несовершенных схемах – необходимостью обеспечения высокой энтропии частного секрета. Но поскольку в несовершенных схемах уже имеется возможность решения дополнительных задач посредством несложных алгоритмов, то объединение асимметричной криптографии с пороговым несовершенным разделением секрета должно иметь больший эффект по сравнению с совершенной схемой.
Представленная работа посвящена развитию пороговых схем разделения секрета на базе Китайской теоремы об остатках, которая позволила бы решить задачи конфиденциальной обработки, передачи, хранения и презентации данных.
Постановка задачи
Модулярная несовершенная схема на базе Китайской теоремы об остатках, предложенная Миньоттом (М. Mignotte) [1], по способу разделения и восстановления секрета эквивалентна способу кодирования информации в непозиционной системе счисления – системе остаточных классов (СОК) [2]. Данное свойство модулярной пороговой схемы позволяет использовать механизмы коррекции ошибок в СОК для верификации данных [3], механизмы параллельной обработки информации для пролонгации по принципу «блуждающих ключей» [4], механизмы масштабирования для изменения числа пользователей и порога схемы разделения секрета [5]. Пороговая схема разделения секрета Миньотта использует специальные последовательности положительных целых чисел
Pa
<-<Р„,
названные (Ли) - последовательность Миньотта, таких, что gcd^^H 1 для всех 1 <
i < j < n
и
P^i-P^Pa-P, >
где
n>2,2
При реализации порогового разделения по схеме Миньотта остаются нерешенными следующие задачи:
-
- обеспечение безопасной передачи частей секрета по открытой компьютерной сети;
-
- в случае объединения частных секретов пользователями, число которых меньше порога, обеспечение высокой энтропии секрета при подборе недостающих частей;
-
- сокрытие от пользователей их истинных частных секретов для сведения к нулю возможности проведения внутренней атаки.
Решение данных задач должно внести в схему Миньотта дополнительные свойства: защита от внутренней атаки, увеличенная энтропия частного секрета, защита частных секретов от несанкционированного доступа.
Защита информации от несанкционированного доступа при передаче и хранении обеспечивается механизмами шифрования и электронной подписи. Анализ известных схем шифрования показал, что симметричное шифрование не подходит для обозначенной модификации, поскольку параллельная обработка частных секретов будет сопряжена с их раскрытием пользователям. Асимметричные экспоненциальные алгоритмы RSA и ЭльГамаля удовлетворяют требованиям к модификации пороговой схемы, что объясняется вычислениями над алгебраической структурой изоморфной алгебре пороговой схемы Миньотта.
Однако RSA и схемы ЭльГамаля обладают высокой вычислительной сложностью. С данной позиции привлекательными являются криптографические алгоритмы на базе эллиптических кривых. Таким образом, можно сформулировать задачу исследования: разработка системы пространственного разделения секрета на базе несовершенной пороговой схемы и шифрования над группой точек эллиптической кривой с обеспечением верификации, пролонгации, динамики пользователей и энтропии частного секрета равного или больше энтропии секрета разделяемого.
Принцип построения пороговой схемы на точках эллиптической кривой
Предлагаемая криптографическая схема получена объединением схемы распределения ключей Месси-Омуры (Massey-Omura) [8] и пороговой схемы Миньотта.
Для построения пороговой схемы Минь-отта потребуется n попарно взаимно простых чисел Pa
рог схемы разделения секрета, и диапазон изменения секрета, определяемый разностью Г t-2t X
Па -Па , будет достаточно большим.
I -=0 /=1 7.
Тогда частные секреты s,. = л mod p,, i = 1 + n. Восстановление секрета может производиться с помощью ортогональных базисов, полиадической системы счисления или позиционных ха- рактеристик [6]. Диапазон представления чисел а = Па, Базовой операцией эллиптической криптографии является умножение точки Q на скаляр: V-kQ, причем по известнымГиб сложно найти k. Данное свойство используется для построения алгоритмов шифрования, электронной подписи, распределения ключей, передачи с забыванием [7] и т.д.
Рассмотрим протокол взаимодействия участников порогового разделения секрета. Функционирование предложенной схемы имеет циклический характер, а каждую итерацию цикла можно разбить на три этапа: разделение, хране- ние и восстановление секрета.
На этапе разделения секрета главный сервер выбирает эллиптическую кривую s(z,). где p – простое число, секретную точку G на E^Zp^ большого простого порядка N, образующую циклическую подгруппу группы точек эллиптической кривой, и публикует свой открытый ключ. Пользователи также публикуют свои от- крытыеключи для обмена сообщениями с сервером. Каждому i-му пользователю сервер ставит в соответствие модуль p^ i = X + n. Взаимно простые числа сервер генерирует или выбирает из списка простых чисел определенной разрядности d. Затем на главном сервере производится поиск точки Q = kG = (x,y) такой, что часть вектора х фиксирована и соответствует разме-t-2 t щаемым данным, а такжеПа-^Па
/=0 /=1
Если точка найдена, то переходим к следующему этапу, иначе производится выбор новой точки G или эллиптической кривой.
На следующем шаге главный сервер разделяет скаляр k :
kv = к mod pv;
k2 = к mod p2;
k„ ее к mod pn и вычисляет частные секреты:
'A, = kxG; A^ = GG.
пороговой схемы, где C' 7 – число сочетаний без повторений из n элементов по / + У:
R^r^G;
R2 = r2P2G;
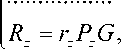
где P„, h = l + Z – h -ый набор модулей, вычеты по которым были объединены для восстановления секрета к, и rh rh, h = 1 + Z – ранг, соответствующий h -му набору модулей для выбранного k .
Для восстановления секрета пользователи, решившие объединить частные секреты, вычисляют скалярное произведение PjAj, i = \ + n и отправляют его результат серверу, используя секретный ключ сервера. Вычисление пользователями скалярного произведения рхА; обусловлено случайным характером образования набора P,„h = X + Z из возможных комбинаций модулей при восстановлении секрета и необходимостью верификации принимаемых сервером данных от пользователей.
Сервер вычисляет скалярные произведе-
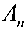
ния Rj=
PpPp
Pi Ph
Pi A, где
Pi
< n, а h – индекс соответствующего на- которые рассылает пользователям, используя их открытые ключи вместе с модулями, которые пользователи должны хранить в секрете. Использование для внедрения данных , нахождение которой требует дополнительных вычислений, а не G, обусловлено необходимостью исключить передачу пользователю координат точки, которая содержит информацию обо всем секрете, даже закрытую с помощью сложной задачи дискретного логарифмирования над группой точек эллиптической кривой.
Секрет восстанавливается только с помощью метода ортогональных базисов, поскольку вычисления в подгруппе точек эллиптической кривой производятся по модулю N , а восстановление числа из вычетов с помощью полиадической системы счисления или основанных на ней позиционных характеристиках содержит вычисления по модулям P„P2-P^ что в предлагаемой криптографической системе невозможно. Поскольку восстановить секрет могут t и более пользователей, сервер по выбранному k вычисляет ранги для z-ic комбинаций модулей /=0
бора модулей. Затем сервер в зашифрованном виде передает каждому i-му абоненту пару ^S,,RhVieI,h-X + Z.
Пользователи могут произвести обмен сообщениями S j и восстановить секрет:
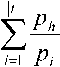
Pi
Ph k_G-rhPhG = kG = Q.
Pi
Длясокращенияобъема передаваемойинфор-мацииисложностивычисленийнасторонеполь-зователя сервер может произвести вычитание двух точек эллиптической кривой fc ->'ЛА для случайного if g I и передать пользователям сообщения VS1>l)..\Sli-rhPhG\.\Slw\ Поскольку точки образуют конечную группу по модулю, результат сложения полученных сообщений будет равен секрету.
Следующий за восстановлением этап подразумевает перераспределение модулей P\,Pn-Pn актуальной разрядности d между пользователями, генерацию значения k , проведение всех вышеописанных этапов вычислений и обмена информацией.
Для того чтобы секрет можно было восстановить методом ортогональных базисов, требуется выполнение условия:
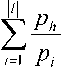
Pi
Ph kjG-rhPhG Pi Pi, Pi где-- Pi Ph Pi = B, — ортогональный базис. log, ££,.£, 1=1 +1 = dtp +1)+и -1, откуда d < Jlog^Ad+2^ и +1 Нарис. 1представленазависимость d = f^ для параметров эллиптической криптосистемы, рекомендуемых различными криптографическими стандартами. дули разрядностью d <--------= 3,25 ; то есть d = 3. Выбираем модулиPa = 5, p, = 6, A = 7, при этом p3 = 7 (2G = (12285,23540): px = 5), (5G = (10931,12316): p2 = б), (3G = (19662,23546): p3 =7). Затем сервер для выбранного k и наборов модулей UaL {a^aL Ьа at {a,a,a} производит вычисления рангов rj = 4, r, = 2, r3 = 3, r4 = 7, на основании которых вычисляет Rx =4-30-G = 120G = (4395,21450), A = 2 ■ 35 • G = 70G = (2568,23364), R3 =3-42-G = 126G = (20688,6550), A =7-210-G-1470G = (27107,30386). Предположим, что второй и третий пользователи решили объединить свои частные секреты. Сервер получит от пользователей следующие данные: от второго получает результат скалярного произведения Рис. 1. Зависимость разрядности модулей от числа пользователей системы защиты данных 6 ■ (10931,12316) = (12376,14398), а от третьего — 7 • (19662,23546) = (29055,10742). Тогда сервер вычисляет -4 =-^- рхр2 =6245-1-42 = 262290, что по модулю N равно 262290mod32117 = 5354,H Pl 32117 Рз РзРз р2р3 =13109-6-42 = Ръ Рассмотрим численный пример. Пусть сервер для построения криптографической системы выбрал эллиптическую кривую E(Z^\.y2 = x3-3x = 119. Выбираем точку G = (22112,9542), которая является генератором подгруппы и имеет порядок ^ = 32117 (разрядность N равна 15 бит). Для построения пороговой схемы «2-из-3» потребуются мо- = 3303468, что по модулю N равно 3303468 mod32117 = 27534. Затем сервер производит скалярное умножение 8Э =5354-(12376,14398)= (3302,17760), А = 27534 ■ (29055,10742) = (9529,18553). Для проверки правильности расчетов и полученных от пользователя данных на этапе восстановления сервер не обязан, но может произвести следующие вычисления. 1. Вычислить ортогональные базисы B^i, В, = 36. 2. Получить результаты скалярных произведений 7-(10931,12316)= (3302,17760), 36 • (19662,23546) = (9529.18553). Сравнить полученные результаты и сделать вывод о целостности данных и правильности вычислений. Сервер отправляет пользователям в зашифрованном виде: второму пользователю {(3302,17760), (20688,6550)1, третьему пользователю {(9529,18552), (20688,6550)}. Теперь пользователи могут обменяться точками эллиптической кривой и произвести самостоятельно восстановление секрета, вычислив (3302,17760)+ (9529,18553)- (20688,6550) = = (13614,14202), и получить секретные данные из координаты x полученной точки эллиптической кривой. Какбылосказаноранее,серверможетнепере-даватькоординатыточки rh PhG каждомупользо-вателю, а «спрятать» ее посредством вычитания к, -^ для случайного Zy G /. Предполо-жим,что серверслучайновыбрал длявычитания точку второго пользователя. Тогда после вычисления S, и S3 сервер производит вычитание (3302,17760)-(20688,6550) = (13626,20747) и в зашифрованном виде передает второму пользователю точку (13626,20747), а третьему – точку (9529,18553). Пользователи, в свою очередь, обмениваются точками и восстанавливают секрет: (13626,20747) + (9529,18553) = (13614,14202). Пример практического применения разработанной пороговой схемы Использование порогового разделения изображений, равно как и видеоданных, сопряженно с необходимостью зашумления картинки, целью которого является сокрытие структуры оригинального изображения в частных секретах [13]. Данный эффект наблюдали авторы при использовании классической схемы Миньотта. Для экспериментального подтверждения отсутствия данного недостатка в предлагаемой схеме было произведено разделение и восстановление изображения. Пороговое разделение секрета большого размера требует предварительного деления секрета на блоки приемлемого размера. Размер блока должен быть меньше разрядности модуля, поскольку блок секрета встраивается в координату x. Также блок секрета должен быть меньше порядка N для обеспечения высокой вероятности наличия в группе подходящей точки для встраивания секрета. Для решения задачи разделения секрета была выбрана эллиптическая кривая E^Z): у2 = x3 + ax + b с параметрами [14]: p = 01FF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 77 = = 2521 -1, 01FF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFC, b = 0051 953EB961 8E1C9A1F 929A21A0 B68540EE A2DA725B 99B315F3 B8B48991 8EF109E1 56193951 EC7E937B 1652C0BD 3BB1BF07 3573DF88 3D2C34F1 EF451FD4 6B503F00, G = 04 00C6858E 06B70404 E9CD9E3E CB662395 B4429C64 8139053F B521F828 AF606B4D 3DBAA14B 5E77EFE7 5928FE1D C127A2FF A8DE3348 B3C1856A 429BF97E 7E31C2E5 BD660118 39296A78 9A3BC004 5C8A5FB4 2C7D1BD9 98F54449 579B4468 17AFBD17 273E662C 97EE7299 5EF42640 C550B901 3FAD0761 353C7086 A272C240 88BE9476 9FD16650, N = 01FF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFA 51868783 BF2F966B 7FCC0148 F709A5D0 3BB5C9B8 899C47AE BB6FB71E 91386409. Разрядность выбранного модуля эллиптической кривой и порядка группы равна 521 бит. Один разделяемый блок был выбран разрядностью 512 бит. Для схемы Миньотта «3-из-5» разрядность одного модуля равна 85 бит. Тогда разрядность в битах скаляра k лежит в диапазоне 170 < [log2 ^] + l < 255. Выбранные модули пороговой схемы px =19342813113834066795298819, p, =19342813113834066795298861, p3 =19342813113834066795298889, p, =19342813113834066795298993, p, =19342813113834066795299063 являются простыми числами. На рис. 2 представлены этапы разделения и восстановления тестового изображения. На этапе разделения изображения на приемлемые блоки сервер производит выбор размера одного блока и формирование массива блоков. На этапе порогового разделения блоков изображения сервер получает частные секреты в соответствии с предложен- ным численным методом: выполняется поиск k, вычисление к;, Ai и Rj, i = 1 + n и распространение частей секрета между пользователями. На рис. 2 на этапе восстановления секрета пользователи под номерами 1, 2 и 3 решили восстановить секрет. Взаимодействуя с сервером и между собой, пользователи получают всю необходимую для восстановления информацию и собирают секрет. Для реализации данного разделения была разработана компьютерная программа для платформы .NET Framework 4.5. Для обработки больших чисел использовалась структура BigInteger пространства имен System.Numerics. Блоки изоб- ражения для внедрения в точку эллиптической кривой конвертировались в строку string, а затем в его эквивалент типа BigInteger. На этапе восстановления секрета производилось обратное преобразование из BigInteger в string, а затем в изображение. Компьютерное моделирование показало, что из частных секретов невозможно выделить структурные фреймы оригинального изображения, что объясняется не только разделением блоков по 64 байта, но и вычислениями над группой точек эллиптической кривой, элементы которой невозможно сравнивать между собой, как числа в классической схеме Миньотта. Пользователь № 1 IM^J^^^ MR^ Xj^ > "Ч^^У1^^®^ I [ользовагель № 2 (ользовагель № 3 Е^^ЫИРП .Пользователь № 4 vПользователь № 5 BBBiajs^G^ М^5Ж><ЭН Этап разделения изображения на приемлемые блоки Эган порогового разделения блоков изображения Этап восстановления секрета Рис. 2. Практическое применение разработанной пороговой схемы Представленная пороговая схема разделения секрета должна обладать всеми преимуществами схемы Миньотта. Рассмотрим изменение числа пользователей, верификацию и пролонгацию предложенной пороговой схемы. Изменение числа пользователей Число пользователей при выбранном порядке группы точек эллиптической кривой влияет на разрядность модулей схемы Минь-отта. В классическом варианте подобная зависимость с ограничением на диапазон изменения секрета приводит к нецелесообразности использования пороговой схемы, поскольку для модулей малой разрядности успех проведения внутренней атаки очень высок. Предложенная пороговая схема может оперировать с модулями малой разрядности, поскольку главный секрет размещен в точке эллиптической кривой. Кроме того, с ростом разрядности выбираемых модулей растет число доступных простых чисел 7Р , где л(х) – функция распределения простых чисел от 1 до x, которое должно соответствовать допустимому числу пользователей системы п< л(2а'). Таким образом, для пороговой схемы, построенной на точках эллиптической кривой, в зависимости от порядка используемой группы точек имеется ограничение на максимальное количество пользователей: для порядка разрядности 128 бит – максимум 15 пользователей с модулями схемы Миньотта разрядностью не более 7 бит, для 256 бит – максимум 27 пользователей с модулями схемы Миньотта разрядностью не более 8 бит, для 512 бит – максимум 50 пользователей с модулями схемы Миньотта разрядностью не более 9 бит. По этой причине корректировка числа пользователей возможна в начале сеанса разделения секрета, которое сопровождается генерацией новых модулей схемы Миньотта. Другой вариант подразумевает создание пороговой схемы с фик- сированным порогом t, но с числом n, которое можно увеличивать до некоторого значения . Причем значение ^max ’ зависимое от разрядности модулей схемы Миньотта, следует определить по статистическим данным использования системы защиты информации. Пролонгация пороговой схемы Предложенная пороговая схема имеет несколько секретных параметров, которые следует обновлять для снижения вероятности успеха внутренней атаки. Все секретные параметры системы могут быть обновлены на этапе разделения секрета. Но поскольку период между разделением и восстановлением секрета может быть недопустимо большим, то для высокой криптостойкости важно проводить пролонгацию на этапе хранения. Ax , A2 ... An могут быть вычислены пользователями системы по полученным от сервера а доп а стар а нов дополнениям Ax At 9 которые сер- (ЛДОП HOB 1 1 • 1 . / = 1+и, в зашифрованном виде. Обновление общего ключа производится после нахождения скаляра к такого, что новый секрет представим в виде 5нов ^нов^" "^ ^стар * Предложенная пороговая схема позволяет произвести данное обновление параллельно и независимо на компьютерах пользователей системы. Верификация и защитаот мошенничества В пороговых схемах главный сервер, распределяющий секрет, является доверенной стороной. Однако секрет может быть сформирован пользователями системы без третьей стороны. Также этап восстановления секрета начинается после обмена частями секрета пользователями системы числом равным или более t или пользователями одной из авторизуемых частными секретами групп. Поскольку частные секреты могут быть искажены как по объективным причинам (технические сбои, помехи), так и в результате умышленных действий одного или нескольких пользователей, разработанная пороговая схема нуждается в механизме обеспечения корректности стадий разделения и восстановления секрета. Выделяют два вида мошенничества в пороговых схемах, при которых: - некоторым пользователям известен секрет, и они пытаются «подсунуть» ложный секрет другим пользователям системы [10]; - пользователям, участвующим в жульничестве, неизвестен секрет [11]. Обобщением данных моделей злоумышленника будет вариант,когда группа неавторизованных пользователей объединяется с группой честных пользователей с целью восстановления секрета таким образом, чтобы честные пользователи сформировали ложный секрет,а мошенники – настоящий секрет. Применение Китайской теоремы об остатках в криптографических схемах дает возможность использования хорошо разработанного аппарата коррекции ошибок в системе остаточных классов (СОК)для верификации критических данных [2]. Избыточности помехоустойчивого кода можно поставить в соответствие пользователей,число которых превышает достаточное для восстановления числа t, то есть (»-0- Чем больше разность (и-/), тем больше ошибок или неправильных частей секрета можно обнаружить. Однако данный подход не применим для случая, когдатолько t пользователей восстанавливаютсекрет или мошенников, участвующих в восстановлении секрета,больше, чем допускают корректирующие свойства СОК.С другой стороны,в предложенной модификации пороговой схемы величины всех начальных, промежуточных и конечных результатов вычислений процесса коррекции ошибок в СОК скрыты и не могут использоваться для сравнения с эталонами. Поскольку значение вычетов по одному или произведению модулей не представляется возможным определить в процессе криптографических преоб-разований,следовательно,в пороговую схему необходимо внести дополнительную информацию о сек-рете,использование которой злоумышленниками не приведет к уменьшению энтропии ключа.Для решения данной задачи можно использовать хэш-код сек-рета,полученный по алгоритму ГОСТ Р 34.11-94.В данном случае каждый пользователь может сравнить хэш-код секрета, предложенный сервером, с хэш-ко-дом, полученным из восстановленного секрета. Хэш-код общего секрета позволяет только обнаружить факт подмены секрета. Для идентификации мошенников потребуется вычисление хэш-кода для каждой части секрета. Заключение Предложенная схема эллиптической пороговой схемы разделения секрета обладает преимуществами несовершенной схемы Миньотта в параллельной обработке частей секрета, пролонгации, верификации, изменения числа пользователей, при этом энтропия части секрета не меньше энтропии ключа. Разработанная схема может быть использована в задачах передачи, хранения, обработки и презентации данных, требующих защиты от несанкционированного доступа. Работа выполнена при поддержке гранта РФФИ 12-07-00482.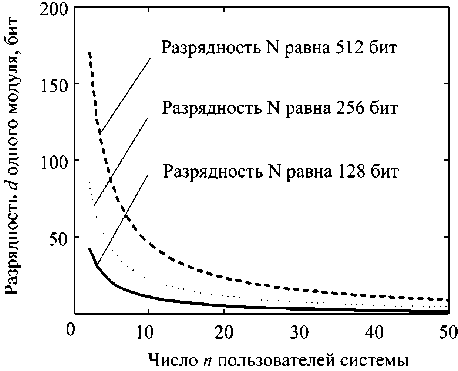

Список литературы Численный метод порогового разделения секрета над группой точек эллиптической кривой
- Mignotte M. How to share a secret//Cryptography-Proceedings of the Work-shop on Cryptography, Burg Feuerstein. 1982, Vol. 149 of Lecture Notes in Computer Science. Springer-Verlag, 1983. -P. 371-375.
- Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. М.: Сов. радио, 1968. -440 с 3-4.
- Steinfeld R., Pieprzyk J. Lattice-Based Threshold Changeability for Standard Shamir Secret-Sharing Schemes//IEEE Transactions on Information Theory. Vol. 53, Iss. 7, 2007. -P. 2542-2559.
- Червяков Н.И., Сахнюк П.А., Шапошников А.В., Макоха А.Н. Нейрокомпьютеры в остаточных классах. М.: Радиотехника, 2003. -272 с.
- Болотов А.А., Гашков С.Б., Фролов А.Б. Элементарное введение в эллиптическую криптографию: Протоколы криптографии на эллиптических кривых. М.: КомКнига, 2006. -280 с.
- Method and apparatus for maintaining the privacy of digital messages conveyed by public transmission//Massey J.L., Omura J.K. Patent US 4,567,600.
- Применение искусственных нейронных сетей и системы остаточных классов в криптографии. М.: ФИЗМАТЛИТ, 2012. -280 с.
- Carpentieri M., Santis A.D., Vaccaro U. Size ofshares and probability of cheating in threshold schemes//In Advances in Cryptology -EUROCRYPT '93. Ser. Lecture Notes in Computer Science. T. Helleseth, Ed. Vol. 765. Springer-Verlag, 1994. -P. 118-125.
- Ogata W., Kurosawa K., Stinson D. Optimum secret sharing scheme secure against cheating//SIAM Journal on Discrete Mathematics. Vol. 20, No. 1, 2006. -P. 79-95.
- Pasaila D., Alexa V., Iftene S. Cheating Detection and Cheater Identification in CRT-based Secret Sharing Schemes//IACR Cryptology ePrint Archive, 2009. Rep. 2009:426. -P. 1-8.
- Upmanyu M., Namboodiri A.M., Srinathan K., Jawahar C.V. Efficient privacy preserving video surveillance//IEEE 12th International Conference on Computer Vision, 2009. -P. 1639-1646.
- SEC 2: Recommended Elliptic Curve Domain Parameters. Standards For Efficient
- Червяков Н.И., Евдокимов А.А. Нейросетевой блок локализации ошибок криптографического нейропроцессора//Нейрокомпьютеры: разработка, применение. № 10, 2004. -С. 54-67.


