Численный метод решения некоторых обратных задач теплопроводности с неизвестными начальными условиями

В прикладных задачах, связанных с исследованием нестационарных тепловых процессов, часто возникает ситуация, когда требуемые величины могут быть измерены только на части границы. Математические модели таких процессов содержат граничные условия, известные только на некоторой части границы и неизвестные на других ее участках. Как правило, для решения этих задач требуется знать начальное условие. Вместе с этим существует целый ряд прикладных исследований, при проведении которых невозможно определить начальные условия. К таким задачам, например, относится исследование электромагнитных и тепловых характеристик работающих двигателей, а также задачи геофизики, связанные с нагревом и охлаждением земной коры. Математические модели таких задач имеют вид обратных граничных задач с неизвестными начальными данными.

Проблеме разработки и исследованию методов решения обратных граничных задач посвящены работы многих исследователей. Так, в работе [1] изложены наиболее распространенные методы решения обратных граничных задач тепломассопереноса, в работе [2] рассмотрены итерационные ре-гуляризирующие алгоритмы ньютоновского типа, в работах [3, 4] рассмотрены методы проекционной регуляризации. Методам решения обратной задачи теплопроводности с неподвижной границей, основанным на применении преобразований Лапласа, посвящены работы [5, 6].

В статье рассмотрена принципиальная возможность построения численного метода решения для обратных граничных задач с неизвестными начальными условиями и предложен новый метод решения такого рода задач. С целью оценки эффективности предложенного метода был проведен вычислительный эксперимент, результаты которого также представлены в данной работе.

Моделирование и компьютерные технологии

Постановка задачи

Пусть x е ( 0, £ ) . Обозначим Q T = ( 0, £ ) x ( 0, T ) для T >  0 . Пусть функции a ( x , t ) , b ( x , t ) , c ( x , t ) е C ( Q_T ) . Предположим, что a ( x , t ) е [ A , a 1 ] , b ( x , t ) е [ b ₀, b 1 ] и c ( x , t ) е [ c ₀, c 1 ] , где A , a 1 , b₀, b 1 , c ₀, c 1 = const >  0 . Оператор L определим следующим образом

Lu = auxx + bux + cu ,   (x, t )е QT .(1)

Пусть функция u(x, t)е C4,2 ( Qt ) является решением параболического уравнения ut = Lu (x, t) + f (x, t) (x, t )е Qt(2)

и удовлетворяет граничным условиям u (0, t ) = P (t), ux (0, t ) = g (t), t е[0, t ].

Требуется найти функцию u(x, t) , удовлетворяющую (2), (3) в области QT , а затем, используя полученные результаты, найти граничную функцию u (£,t) = ф(t),     t е[0,T].(4)

Предположим, что при некоторых f (x, t) = f0(x, t), p(t) = p0(t) и g (t) = g0(t) существует функция u0(x,t), удовлетворяющая (2), (3) и известно, что ф(t) е H2,1+в (0,T), где в е (0,1), тогда из результатов, представленных в работах [7] и [8] следует единственность решения задачи (2)-(4) в некоторой области QT с QT. Предположим также, что существуют константы Ф, в, R такие, что max|u(x,t)| <Фeв(x+t),    {maxutt |,max|u„|,max\uxx„} < R.                                    (5)

Q T                           Q T        Q T        Q T

Для решения поставленной задачи предложен метод дискретной регуляризации. Идея метода состоит в следующем. Решение исходной задачи сводим к решению уравнения

Lu + a u = f ,                                                                            (6)

с граничными условиями (3), где a - некоторый параметр регуляризации. Далее в области Q_T вводим конечно-разностную сетку, состоящую из узлов ( x i , t k ) , i = 1, N_x + 1, k = 1, N_t + 1 и заменяем уравнение (6) в каждом узле сетки ( x_i , t_k ) его конечномерным аналогом. Затем, используя явные конечно-разностные схемы, получаем значения искомой функции на новом пространственном слое в точке ( x i _{+ 1}, t_k ) .

Одномерный метод дискретной регуляризации

Рассмотрим конечно-разностную сетку G в прямоугольнике Q_T ,

G Ч

( ^xi , t k ) : ^x = ⁽ i ^- 1) h x ,

t = ( k — 1) h_t ,

h_x = £ / N_x ; h t = T / N_t ;   i = 1, N_x + 1; k = 1, N_t + 1,

где h_x и h_t – шаги сетки по переменным x и t соответственно. Рассмотрим множество дискретных функций V_h = { v ( x i , t_k ) = v_ik } , заданных на G . Следуя подходу, предложенному Самарским в работе [9], конечно-разностный аналог частных производных по x и по t в каждой точке G определен следующим образом:

,i , k = v i +y---- / ,1 , i = 1, n , k = 1, n + 1;

x      xt hx i, k    vi, k+1    vi, k vt   =------i------- ht

i = 1, N x + 1, k = 1, N t .

i, k _ vi+1, k   2 vi, k + vi-1, k vxx =           , 2

h

i = 2, N x , k = 1, N t + 1

Используя формулу Тейлора, получаем, что при любых u(x, t) е C4,2 (QT) конечно разностные аналоги (8) аппроксимируют частные производные с точностью O (hx) для дx, и O (h2) для д2 при h ^ 0, а дt аппроксимируется с точностью O (ht) при ht ^ 0 .

Обозначим значения функции f е C(QT) в соответствующих точках (xi, tk )е G как fik, значения коэффициентов оператора L в этих же точках обозначим ai,k, bi,k, ci,k , а значения функции u (x, t) е C4,2 (QT) в точке (xi, tk )е G обозначим как uik .Частным производным д2x, дx, дt сопоставим конечно-разностные аналоги, определенные формулами (8). Тогда конечно разностный аналог уравнения (2) при i = 2, Nx +1, k = 1, Nt имеет вид

1 /               х    a i , N_t +1                              A b i , N_t +1 (              А                 г                 /лх

T"(vi,k+1 - vi,k ) =     2   (v i+1,k — 2vi,k + vi—1,k ) +   ,----( vi+1,k — vi,k ) + ci,k vi,k + fi,k, ht                   hxh где йi k - дискретная функция. При i = 2, Nx +1, k = Nt +1 уравнения (2) имеет вид

1 /              X ai, Nt +1 V            a .V

3 (vi,Nt +1 vi,N ) =         y( vi+1,N +1 2vi,N +1 + vi-1,N +1) + tt         t    tt

t

, bi,Nt +1 V                                                      . ai,Nt

+ —;---Y( vi+1, N+1 — vi, N +1) + Y ci, N +1 vi, N +1 +4fi, N+1 + "T2-(1 — y)( vi+1, N - 2 vi, N + vi-1, N ) + t      t         tt       t                   t      tt xh

+ bi;NL (1 - Y)(vi+1,Nt - vi,Nt ) + (1 - Y)ci,Nt vi,Nt + (1 - Y)f-,Nt , hx а условиям (3) соответствуют следующие соотношения:

v1,k = Pk, v2,k - v1,k = hxgk,     k = 1, Nt + 1, где vi,k – дискретные функции, соответствующие конечно-разностным аппроксимациям в точке (xi,tk) е G функции u(x,t) е C4,2 (QT), удовлетворяющей (2), (3).

Известно, что предложенная схема неустойчива, поэтому мы добавим в (9), (10) слагаемое, содержащее параметр регуляризации а> 0, и выразим vi+1k из уравнений (9), (10) при i = 2, Nx +1 и k = 1, Nt +1. Тогда при i = 2, Nx +1, k = 1, Nt получим:

ai,k vi+1, k    2         ,    , ai, k + bi, khx

v i , k

ai,k ai, k + bi, khx

v i - 1, k

₊       hx"       ₍ v

^{( a}i , k ⁺ b i , k h x ) h t   i , k ^{+ 1}

^- v i , k ^{) +}

h 2 b i, k               h 2 ^ci, k         ,      h x ²«                 h x²

v i k v i k ⁺ v ,- k f i ^ai , k ⁺ b , k h x ,      ^ai , k ⁺ b , k h x ,      ^ai , k ⁺ b , k h x   ,      ^ai , k ⁺ b i , k h x

1+a,k- h2ci,k -       hx ai,k + b,khx   (ai,k + b,khx )ht

v i , k

—

a i , k

a i , k

+ Ь к hx i , k x

v -1, k ⁺

h 2                a h 2              h 2

-----:—г-^Vi k +1-- :—— v k--x——

(ai, k + bi, khx ) ht   ,       ai, k + bi, khx   ,     ai, k + bi, khx а при i = 2, Nx +1 и k = Nt +1 имеем:

Моделирование и компьютерные технологии vi+1, Nt +1 = /

( a i , N t +1

^hx ²

⁺ h x b i, N t +1 ) h t Y

⁽ v i , N t +1

^— v i,N t ) ⁺

a i, N t ^{+ 1}

_a + hb     ( 2 v, Nt + ¹

a i , N_t +1 ⁺ h x b i , N t +1

—

v i —1, N t +1 ) ⁺

h x b i , N t +1

a i , N t +1 ⁺ h x b i , N t +1

^hx c i , N +1                        h 2

-----TTu vi , Nt +1 ^—  ---- TTu a i , N_t +1 ⁺ h x b i , N_t +1             a i , N_t +1 ⁺ h x b i , N_t +1

—

^hx ²

( a i , N_t +1 ⁺ h x b i , N_t +1 ) Y

(1 — Y )

a i , N t                                            b i , N t

2   ⁽ v i +1, N t   ² v i , N t ⁺ v i —1, N t ) ⁺ ,     ⁽ v i +1, N t    vi , N t )

h x                               h x

—

—

h ²

( a i , N_t +1 ⁺ hb i , N_t +1 ) Y

^{(1 —} Y ) [ c i , N_t v i , N t

⁺ fi , N t ⁺] ^—

a h ²        v

( a i , N_t +1 ⁺ hbi , N_t +1 ) y *, ‘

где vi,k – дискретные функции, полученные из конечно-разностных уравнений (12), (13) при условии (11). Уравнения (12), (13) эквивалентны добавлению слагаемого aU в (10), (11). Метод дискретной регуляризации заключается в следующем. На первом этапе, используя (11), определим v1,k , v2,k как v1, k = Pk,   v2, k = Pk + hgk,     k = 1, Nt + 1.                                                       (14)

Затем, используя (12) и (13), находим v_{i , k} в остальных узлах сетки.

Алгоритмические особенности метода

Оценим уклонение функций v_{i , k} от u_{i , k} в области Q_T . С этой целью введем в рассмотрение функции s_{i , k} , w_i , определяемые формулой:

s i , k = ^vi , k ^{— u}i , k , w i = max I v i , k ^{— u}i , k I, i = 1, ^Nx ⁺ 1, ^k = 1, ^Nt ⁺ 1,

k где vi,k удовлетворяет (12), (13) с условиями (14), а ui,k удовлетворяет (2), (3). Естественно пола- гать, что для любого i = 1, Nx имеет место неравенство wi < wi+1. Учитывая (14), получаем сле- дующие оценки:

w 1 <8 , w ₂ <8 (1 + h ) + O ( h ) <8 + Rh.

Подставив (12) в (2), мы получаем при i = 2, Nx и k = 1, Nt si+1, k

a h 2

+----x^^u,k = ai, k + bi, khx ,

.   a i , k ^— h^{2(1 +} c i , k )           h¹

1 +---- ai, k+ bi, kh        (ai, k+ bi, kh )t

s i , k

—

ai,k ai, k+ bi, kh

s i —1, k

+

h x ²

⁺ ^--------- ;----, , , si k +1 +

⁽ a i , k ⁺ b i , k h x ) h t   ,        a i , k

a h ²             a h ²

~Tin:r+ k ⁺ TTlTui, k ⁺ O ( h^{2 +} ht ) . ⁺ b i , k h x         a i , k ⁺ bi , k h x           ^V         ’

Если a_ik — h 2 (1 + c_ik ) >  0 при всех i = 3, N_x + 1 и k = 1, N_t , то, выполняя соответствующие

преобразования и учитывая, что w i <  w i _{+ 1} и a i _k , b i _k , c i _k >  0 при всех i = 3, N_x и k = 1, N_t , из по-

следнего неравенства имеем:

a hx si+1, k +      7T tT ui, k < ai, k + bi, khx

+ 2 h x - + ^{a h}x -) w + ^a h x- ф e ^e ( ^{x +} t ) + R^h 2 + h_t ).

Aht    A i A                x t

C другой стороны, s i _{+ 1} k +

a h 2

x     ui k ai, k + bi, khx   ,

> max | s i +1, k|

—

a h 2       I I

—x - max | u i , k | >  w +1

A i , k

—

^a h x ф e P( ^{x +} t ) A .

Отсюда и из (16) следует, что wi+1

+ 2h x- + ^ h ^) w + ^{2 a} h x - Ф e ^{e ( x +} t ) + R (h_x ² + h_t ), i = 2, N_x .

Aht    A i A                 x t           x

» 2 h ² a h ²

Обозначим C = 3 +---+--- , тогда последнее неравенство примет вид

A т A wi+]< Cw, + 2ahx Фee(x+t) + Rh2 + h V i = 2, N . i+1 i a                       \ x t )7          7 x

Оценим Wn _{+ 1}, используя (15) и (17), получаем

W N x +1 <  C N x

1 ( 8 (1 + h x ) + Rh x ) +

V

^{2 a} h x _ф e ₽( x + 1 )

A

A N_x -2

+ R ( h x + h t ) £ C

7 m =0

- m <

< C N x ^{- 1}

(

8 (1 + h x ) +

V

^A p Ф e^{x +} t ) + R ( h x + h t + h x ) .

Выберем h_x , h_t и

2 h ²

так, что Ah <  1 и —— < 1, а параметр а выберем таким, что ^t           Ah_t

^ ^ ф ф _е ^{e ( x +} t > < 8 , тогда A

C <  5 и (18) примет вид

w . +1 <  5 N x

-1

< 2 . 5 N x

-1

Согласуем величины Nx и ht с уровнем погрешности 8 так, чтобы гарантированно было выполнено условие wN +1 < VM8 для некоторого M > 0. Для этого выберем Nx таким, что при некотором H > 3 для величины M > 0 такой, что M > 48 • 52H, имеет место соотношение

N_x <  1 + log₅ —;------ . Отсюда следует, что, для соблюдения условия w_{N + 1} < V M 8 дос

2 .(8 + 2R^Aht)

таточно выбрать величины h t , h_x и а из следующих условий:

8 VM г; ,2 Ah,A

ht <---т —S"-V8 , h2 < —L a<—5—— .

t 4 AR ² V 2-5 ^H       7 x 2        2 Н 2 Ф e ^{e ( x +} t )

Предложенный алгоритм послужил основой для разработки программного комплекса [10]. С целью проверки достоверности полученных результатов и оценки эффективности предложенной схемы был осуществлен вычислительный эксперимент. Эксперимент проводился для серии тестовых функций. В каждой серии проводилось по несколько повторных расчетов для каждой функции.

Вычислительный эксперимент

Основной целью вычислительного эксперимента являлась проверка принципиальной возможности построения регуляризованных решений обратных задач с неизвестными начальными условиями методом дискретной регуляризации. Объектами вычислительного эксперимента являлись построение во всей области Q_T численного решения задачи (2)–(4) с последующим вычислением соответствующей граничной функции (4). С целью получения экспериментальных оценок погрешностей были вычислены величины отклонения найденных граничных функций от тестовых значений.

На начальном этапе эксперимента была решена следующая прямая задача:

Lu = f, u (0, t) = p(t), u (I, t) = ф(t), u (x,0) = q(x), x e (0, ^), t g (0, T),                                (20)

решение которой использовалось при оценке эффективности метода дискретной регуляризации. Вычислительный эксперимент проводился для серии тестовых функций, различных с точки зрения монотонности и непрерывности самой функции и ее производной. В каждой серии проводилось по несколько повторных расчетов для каждой функции. Во всех тестах мы полагаем t = 1, а T = 1,5 . Для численной реализации метода выбирается равномерная сетка G , заданная формулой (7)

Моделирование и компьютерные технологии с параметрами ht, hx и а , удовлетворяющими (19). Основные этапы вычислительного эксперимента состоят в следующем:

• 1.    Для тестовой функции решаем прямую задачу (20) методом конечных разностей. Получаем функцию u_test ( x , t ) .

• 2.    Моделируем значение g ₈ в каждой точке t k = ( к - 1 ) h_t по формуле g ₈ ( t k ) = g ( t_k ) + e ₈ ( t_k ), где e ₈ ( t_k ) равномерно распределена на интервале [ g ( t_k ) -8 ; g ( t_k ) + 8 ] .

• 3.    Решаем задачу (2)–(4) методом дискретной регуляризации. Получаем регуляризованное решение и а ( x , t ) во всей области Q T , затем вычисляем граничную функцию и 8а ( I , t ).

  4. Вычисляем величины

  
  

||и 8а ( £ , t ) - ф ( t )|| , где ф ( t ) - тестовая функция.

Результаты вычислительного эксперимента для некоторых тестовых функций проиллюстрированы на нижеприведенных рисунках. Одномерные графики демонстрируют результаты вычислений граничной функции и (1, t ) = ф ( t ), являющиеся решением задачи (2)-(4). Двумерные поверхности, названные "Exact solution" изображают графики функций u ( x , t ) , полученной на основе тестовых функций и являющейся решением прямой задачи (20), а поверхности, названные "Regularized solution" соответствуют регуляризованному решению и 8а ( x , t ) задачи (2), (3), полученному во всей области Q_T методом дискретной регуляризации при неизвестных начальных условиях. Ось абсцисс соответствует значениям пространственной переменной временной x е [0,1], ось ординат - переменной t е [0; 1,5], а ось аппликат связана со значениями функций и ( x , t ) и и 8а ( x , t ).

На всех рисунках используются одинаковые обозначения. Величина погрешности исходных данных, при которой проводились расчеты, обозначена 8. Величина а соответствует величине параметра регуляризации, в методе дискретной регуляризации. Обозначение u (1, t ) соответствует точному значению граничной функции и (1, t ) = ф ( t ), а и 8а - граничной функции, найденной из численного решения и ( x , t ) задачи (2)-(3) в точках ( £ , t ) , полученного методом дискретной регуляризации.

Пример 1. В этой серии экспериментов в качестве тестовые функции использовались непрерывные гладкие функции с одним экстремумом.

На рис. 1, a изображены результаты численного решения обратной задачи (2)–(4) для тестовой функции и ( 1, t ) = t ( e ^- t - e ^{- 1} ) . На рис. 2 изображена поверхность, соответствующая численному решению задачи (2), (3), полученному методом дискретной регуляризации при неизвестных начальных данных, а также поверхность "Exact solution", соответствующая решению прямой задачи (20).

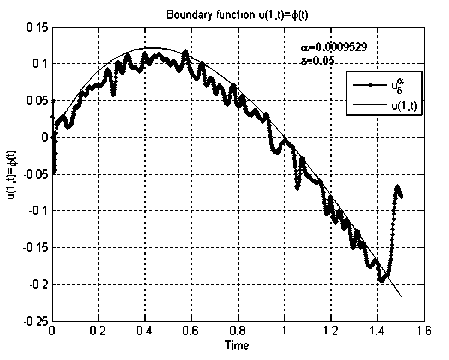
a)                                                                       б)

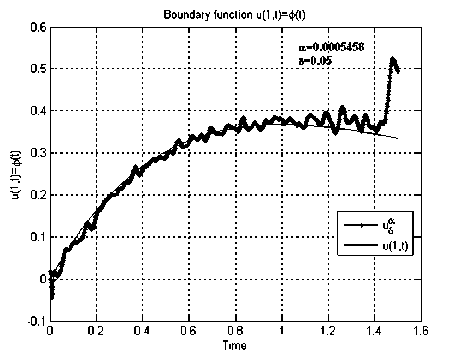
Рис. 1. Граничные функции, полученные в результате численного решения обратной задачи (2)–(4) для тестовых функций из примеров 1, 2

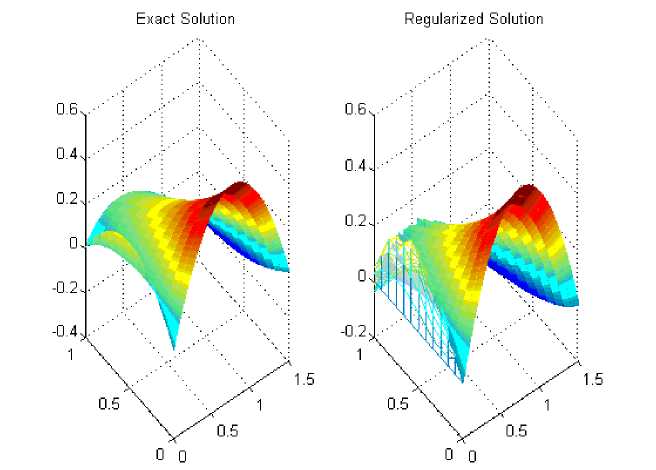
Рис. 2. Результаты численного решения обратной задачи (2), (3) во всей области Q_T , полученные для тестовой функции из примера 1

Пример 2. В проведенной серии экспериментов рассматривались непрерывные функции с разрывными производными.

На рис. 1, б представлены графики численного решения обратной граничной задачи (2)–(4)

для тестовой функции и ( 1, t ) =

^1 ( e - 1 ) - 1, t >  о,

. Рис. 3 иллюстрирует результаты численного

0,

t = 0.

решения задачи (2), (3) во всей области Q_T . Этому решению соответствует поверхность "Regularized solution", а поверхность "Exact solution" соответствует решению задачи (20) для этой же тестовой функции.

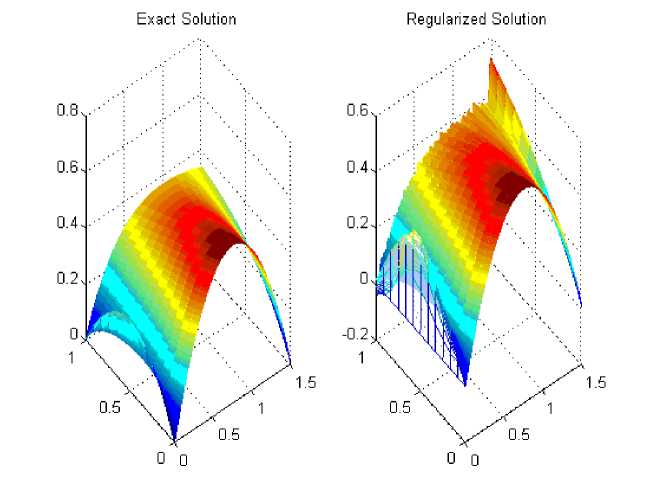
Рис. 3. Результаты численного решения обратной задачи (2), (3) во всей области Q_T , полученные для тестовой функции из примера 2

Моделирование и компьютерные технологии

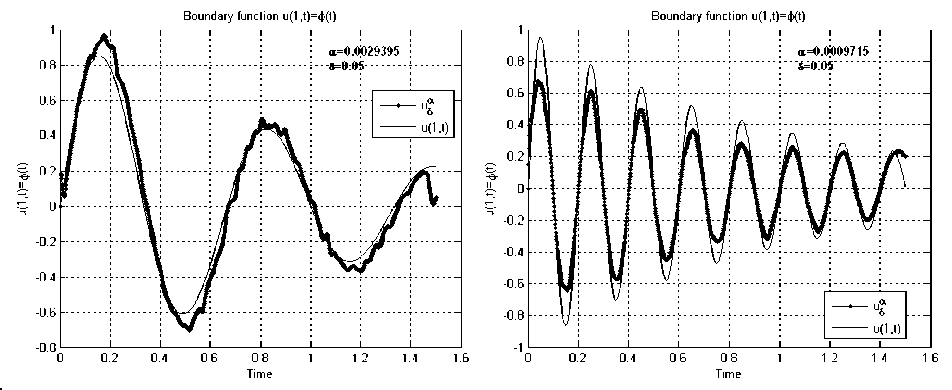
Пример 3. В этой серии в качестве тестовых функций рассматривались непрерывные гладкие функции с несколькими экстремумами. На рис. 4, a изображены результаты численного решения обратной граничной задачи (2)-(5) для тестовой функции и (1, t ) = te - t sin(3 n t ). Рис. 5 иллюстрирует результаты численного решения задачи (2), (3), полученному во всей области Q_T методом дискретной регуляризации.

a)

б)

Рис. 4. Граничные функции, полученные в результате численного решения обратной задачи (2)–(4) для тестовых функций из примеров 3, 4

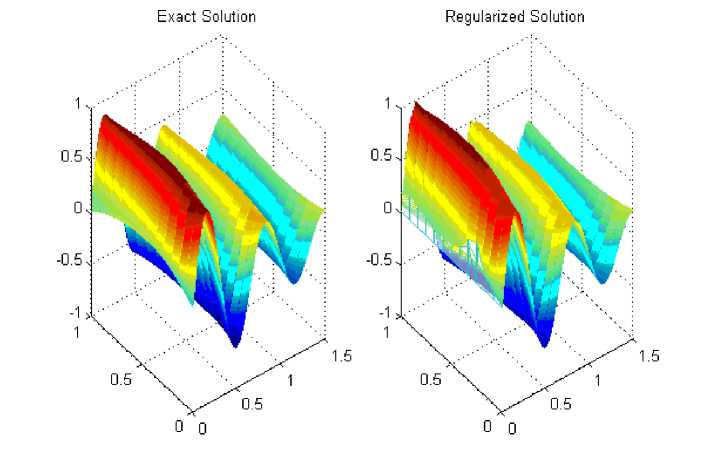
Рис. 5. Результаты численного решения обратной задачи (2), (3) во всей области Q_T , полученные для тестовой функции из примера 3

Пример 4. В этой серии в качестве тестовых функций рассматривались непрерывные гладкие осциллирующие функции с несколькими экстремумами. На рис. 4, б изображены результаты численного решения обратной граничной задачи (2)–(5) для тестовой функции и(1, t) = e-t sin(10nt). Рис. 6 иллюстрирует результаты численного решения задачи (2), (3), полу ченному во всей области QT методом дискретной регуляризации.

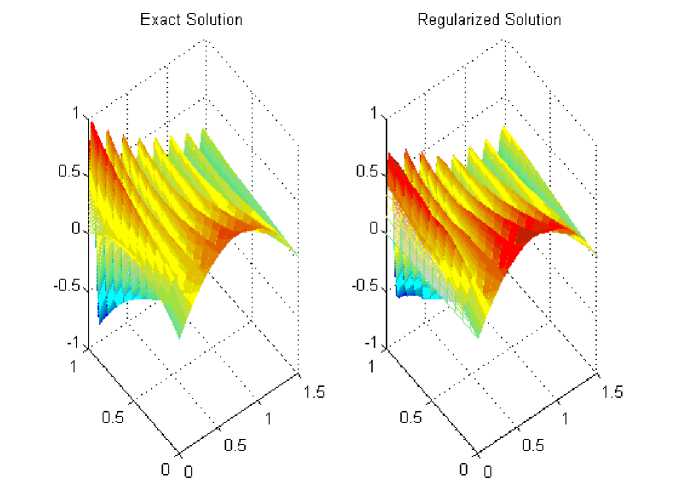
Рис. 6. Результаты численного решения обратной задачи (2), (3) во всей области Q_T , полученные для тестовой функции из примера 4

С целью получения экспериментальных оценок погрешностей численного решения задачи (2)-(4) в каждой серии экспериментов были найдены величины || u ^ ( A t ) -ф ( t )|| Средние значения этих величин, полученных в каждой серии эксперимента, представлены в таблице.

Экспериментальные оценки погрешностей

Тестовая функция		Величина 5	u ъ (^t ) -ф ( t ) C
u ( 1, t ) = t ( e ~ t - e 1)		0,01	0,0204
		0,03	0,0708
		0,05	0,1506
u ( 1, t ) = •	1 ( e t - 1 ) - 1, t >  0, 0,             t = 0.	0,01	0,0211
		0,03	0,0698
		0,05	0,2131
u (1, t ) = te t sin(3 n t )		0,01	0,0230
		0,05	0,0712
		0,1	0,2278
u (1, t ) = e ~t sin(10 n t )		0,01	0,0203
		0,05	0,1903
		0,1	0,2307

На основании полученных результатов эксперимента можно сделать следующие выводы. Метод дискретной регуляризации, предложенный в статье, позволяет получать регуляризованные решения при неизвестных начальных данных с удовлетворительной точностью. Более того, с помощью этого метода становиться возможным не только найти граничную функцию, но и построить приближенное решение обратной граничной задачи во всей области устойчивости при неизвестных начальных данных. Эти особенности метода дискретной регуляризации являются несомненным преимуществом предложенного метода дискретной регуляризации.

Моделирование и компьютерные технологии

Заключение

В статье предложен метод решения обратных задач с неизвестными начальными данными. Метод дискретной регуляризации, предложенный в статье, позволяет получать регуляризованные решения во всей области при неизвестных начальных условиях, а также находить неизвестные граничные функции. Применение этого метода позволило впервые получить решение обратных задач при неизвестных начальных условиях. Экспериментальные оценки погрешности полученных решений свидетельствуют о достаточной устойчивости численных решений.