Численный метод установления соответствия между начальными точками локально асимптотически эквивалентных систем

При проведении численного моделирования химических процессов зачастую приходится сталкиваться с проблемой решения жестких по части компонент нелинейных систем обыкновенных дифференциальных уравнений. Решение задачи Коши для таких систем требует применения особых методов, но даже использование специализированных методик не дает приемлемого сокращения временных затрат при проведении численного эксперимента. В данном случае удобно использовать систему, локально асимптотически эквивалентную исследуемой. В качестве такой системы можно использовать линейное 1

приближение. Такой подход изложен в работах [1-4], где приведены достаточные условия асимптотической эквивалентности для систем обыкновенных дифференциальных уравнений. Рассмотрим нелинейную систему обыкновенных дифференциальных уравнений f x 1 = —k 1 x 1 — 2k₂x 1 ²

^x 2 ^x 3

- x4

= k1x1 + k2x12

= k1x1

= 2k2x12

.

Здесь t > 0; x ^ - концентрации веществ С₂Н₆, С₂Н₄, Н₂, СН₄ соответственно, x ^ >  0, (1 = 1,4); k 1 > 0, k₂ > 0 - константы скоростей химических реакций. Система (1) соответствует кинетической модели брутто-реакции пиролиза этана [3, 5, 6]. Рассмотрим задачу Коши с начальными данными x 1 (0) = 1, x₂(0) = 0, x₃(0) = 0, x₄(0) = 0 для системы (1).

В векторной форме данная система имеет вид:

x = Ax + P(x),

где х = colon(x1, x2,x3,x4).

2k2x1

А =

/—k 1   0  0  0\              /-Zk₂x2\

(k1  0  0  01-    р(х)=( k2X12  )■

\ 0    0  0  0/              \ 2k2x12 /

2k₂x 1

Ее линейное приближение имеет вид:

к У 1 = -к 1 У 1

I ^у 2 = ^к 1 У 1

I Уз = к1У1  ■

V ^У 4 = ⁰

Локальная покомпонентная асимптотическая эквивалентность для систем (1) и (2) показана в [3].

Ставится задача о нахождении начальных данных для системы (2) через известные начальные данные системы (1).

В работе [4] построено отображение, устанавливающее соотношение между начальными точками исследуемой системы и ее линейного приближения:

+ ю

y<0>=x<0> + J Y(-s)P(x(s))ds, 0

где x(t) = x(t:0,x(0)), y(t) = Y(t)y(0), Y(t) приближения.

–

фундаментальная матрица линейного

Для системы (2) она имеет вид:

y(t) =

( o~kit 1-е-^к1 1 - e~^k1t

0  0

)

Отображение (3) в координатной форме имеет следующий вид:

п + ^ю

У^ = А^+^\ y_ij⁽-s)P j (x⁽s))ds,i = 14,               (4)

J = 1 о где yij(t) - элементы фундаментальной матрицы Y(t) системы (2).

Представим отображение (3) в виде п b                       п +ю y^ = x(0) + ^Jyij(-s)Pj(x(s))ds + ^J yij(-s)Pj(x(s'))ds, J = 1 0                            J = 1 b где b определяется из условия [4]:

,     ¹ i (2^kc^co\

^kl'ny—)

при этом c₀ из формулы (3.8) из работы [4].

Таким образом, п b у?0 = x(0 + ^J yij(-s)Pj(x(s))ds.                      (5)

J = 1 о

Для численного решения системы (1) применялся (4,2)-метод [7; 8], для вычисления интеграла из выражения (4) использовался метод Симпсона [9; 10].

Расчет начальных точек для системы линейного приближения проведен для различных значений констант скоростей химических реакций к1 и к2, которые соответствуют протеканию реакции пиролиза этана при различных температурах и рассчитаны из уравнения Аррениуса [5]. Результаты, рассчитанные с точностью £ = 0.001, представлены в таблице.

Таблица

Расчет начальных точек для решений системы линейного приближения

Т,К	800	900	1000	1200
к 1	0.503	32.832	928.979	139822
к 2	0.073	6.625	244.927	55056.8
У0	0.777	0.875	0.790	0.989
У °	0.169	0.091	0.150	0.005
У0	0.115	0.058	0.090	0.000
У0	0.121	0.069	0.118	0.010

На рисунке приведены графики решений систем (1) и (2), между начальными значениями которых установлено соотношение в соответствии с формулой (4), при значениях к 1 и к₂, соответствующих температуре Т = 1000 К.

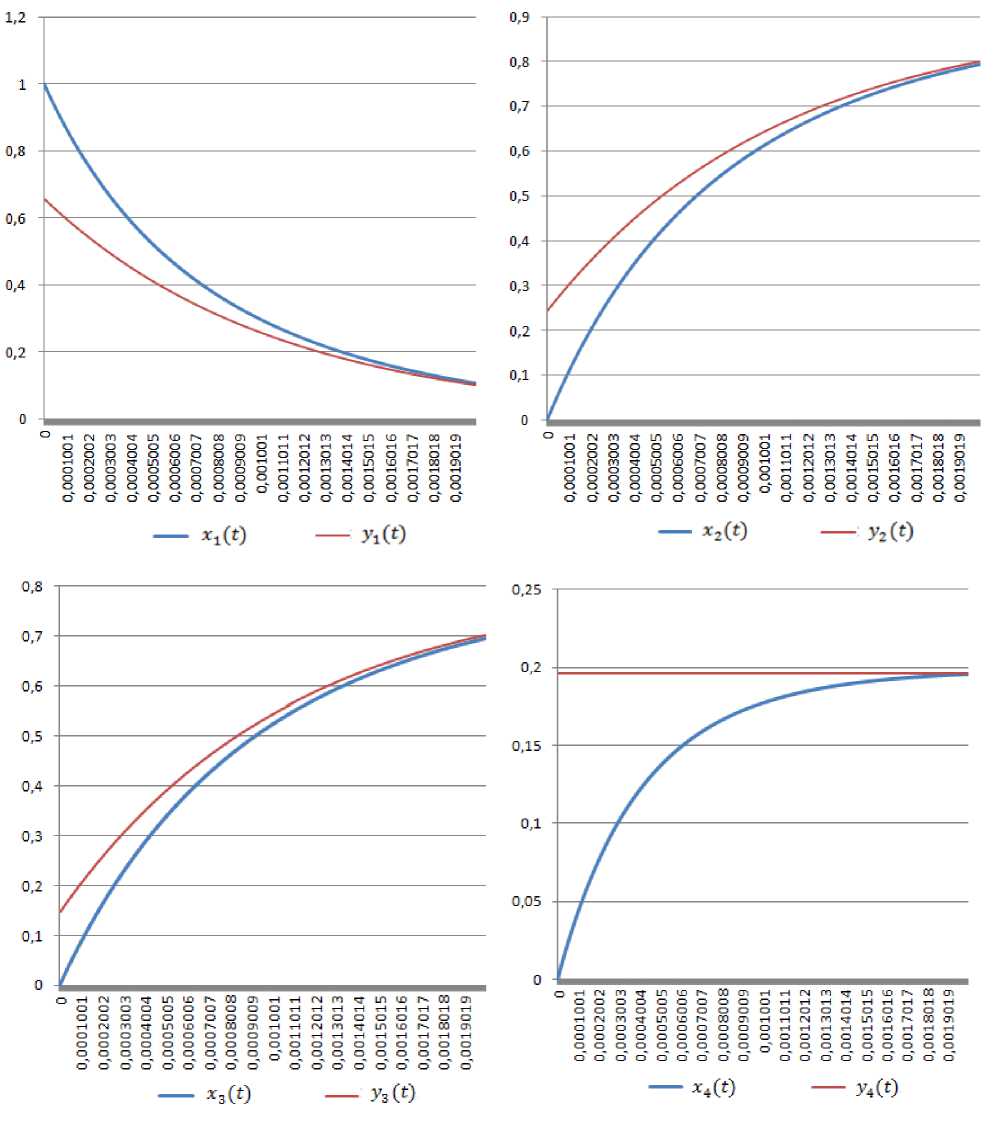
Рис. Графики решений Xi(t) и yi(t), между начальными значениями которых установлено взаимно-однозначное соответствие.

Таким образом, по начальным точкам нелинейной системы обыкновенных дифференциальных уравнений были рассчитаны начальные точки ее линейного приближения, которые обеспечивают локальную покомпонентную асимптотическую эквивалентность систем согласно формуле (4).

Из численного эксперимента видно, что поведение решений системы (1), начиная с момента времени равного 0,002 с, мало отличается от поведения решений системы (2). Это обуславливается достаточно большими значениями констант скоростей химических реакций при температуре 1000 К, а, следовательно, и высокой скоростью протекания стадий химического превращения.

Данная методика позволяет при проведении расчетов использовать вместо численного решения жесткой системы аналитическое решение ее линейного приближения, что значительно сокращает требования к вычислительным мощностям и повышает точность расчетов.