Что дает обращение к японской философии при описании местных сообществ?

Как известно, тиреоидные гормоны оказывают существенное влияние на гемодинамические параметры организма, в частности, на скорость кровотока, артериальное давление, общее периферическое сопротивление кровеносных сосудов [1, 3, 7]. Уменьшение периферического сопротивления сосудов обусловлено воздействием гормона трийодтиронина на гладкую мускулатуру сосудов и приводит к снижению артериального давления, повышению объема циркулирующей крови и эритроцитарной массы, скорости кровотока и увеличению фракции сердечного выброса. Изменения параметров гемодинамики щитовидной железы при гипер- и гипотиреозе, а также под влиянием тиреостатической или заместительной терапии могут использоваться, наряду с анализом клинической картины, исследованием гормонального тиреоидного статуса и рефлексометрией в качестве дополнительных критериев оценки функциональных нарушений щитовидной железы при тиреоидной патологии [2, 4-6, 8, 9].

Однако, несмотря на то, что механизмы изменений гемодинамики при тиреоидной патологии известны, до настоящего времени нет единого подхода к количественной оценке этих изменений. Так, гемодинамические уравнения, описывающие состояние кровотока и повторяющие известные уравнения гидродинамики, составлены для идеальной жидкости, каковой кровь, как известно, не является. Основополагающим соотношением, используемым для описания кровообращения, а также для построения соответствующих моделей, является формула Хагена – Пуазейля, которая устанавливает зависимость объемной скорости течения жидкости от диаметра цилиндрической трубки, а также от их гидродинамического сопротивления:

πR4Δp 8ηl где Q – объем жидкости, протекающей через сосуд за единицу времени, R – радиус трубки, Δp – разность давлений на концах трубки, l – длина трубки, η – вязкость жидкости.

Вместе с тем, существуют ограничения, а также условия применимости уравнений гидродинамики в живых системах, поэтому их произвольное применение может привести к искажениям при описании физиологических процессов в системе кровообращения. Показательным примером является работа, опубликованная врачами Бирмингемской больницы (Великобритания) и больницы С. Мота при Мичиганском университете (США). Статья вышла под названием «Закон Хагена - Пуазейля - факт или вымысел» [10]. В работе указывается, что формула Хагена - Пуазейля, устанавливающая зависимость объемной скорости кровотока от диаметра кровеносного сосуда, не дает реальной картины происходящего. В частности, из этой формулы следует, что при увеличении диаметра сосуда вдвое объемная скорость кровотока увеличивается в 16 раз. Однако эксперимент, проведенный врачами с использованием инфузионных капельниц, показал, что при увеличении диаметра канюли с 1 мм до 2 мм, т.е. вдвое, объемная скорость истечения раствора увеличивается в 6 раз, а не в 16, как это должно быть. Здесь же сказано, что формула, полученная Ж.М. Пуазейлем около 200 лет назад, была слепо внедрена в клиническую практику без экспериментальной проверки. Статья заканчивается фразой: «Сколько еще других "законов" мы используем в клинической практике, которые никогда не были подтверждены?».

Цель исследования. Целью работы является изучение особенностей течения жидкостей в прямолинейных трубках, проверка корректности формулы Хагена - Пуазейля, а также условий её применимости. При этом ставились следующие задачи:

• -    провести измерения объемной скорости течения жидкости по магистралям при постоянной разности давлений на ее концах в зависимости от длины магистрали; повторить измерения для магистралей различного сечения;

• -    провести теоретический расчет указанных зависимостей для магистралей заданной длины и сечения с использованием формулы Хагена - Пуазейля;

• -    провести сравнительный анализ экспериментальных и расчетных данных, проверить справедливость следствий из формулы Хагена – Пуазейля, установить условия и границы её применимости при описания кровообращения.

Материалы и методы исследования. Для проведения измерений использовалась лабораторная установка, состоящая из емкости с водой, соединяющейся с мерной емкостью для сбора воды с помощью полихлорвинилового шланга. Время прохождения жидкости через магистраль измерялось секундомером. Разность давлений на концах магистрали в ходе эксперимента поддерживалась постоянной с помощью клапанного устройства, контролирующего уровень воды в емкости.

Для эксперимента использовалась обезгаженная вода, поскольку в обычной воде содержится значительное количество растворенного газа, который при прохождении через трубку выходит в свободное состояние, образуя на стенках большое количество пузырьков, искажая наблюдаемую картину и вызывая большой разброс измеряемых данных.

После калибровки магистралей, сборки установки, промывки системы этиловым спиртом и заполнения ее обезгаженной водой приступали к измерениям. Пуск воды осуществлялся с помощью затворного клапана с одновременным включением секундомера. После прохождения заданного объема воды секундомер выключался. Исходная длина магистрали варьировалась от 3 до 0,2 метров. В эксперименте использовались трубки диаметром 1,5 мм и 3 мм. Объемная скорость тока воды определялась делением объема прошедшей через систему жидкости в миллилитрах на время ее прохождения в секундах. Измерения для каждой длины шланга проводились по 5 раз, а среднее значение объемной скорости течения жидкости определялось статистической обработкой данных отдельных измерений с использованием критерия Стьюдента для малой выборки при надежности 95%.

При определении интервалов значений длины шланга исходили из того, что изучаемые закономерности должны были охватывать значения числа Рейнольдса, соответствующие как турбулентному, так и ламинарному потоку жидкости с тем, чтобы было возможно определить границы, при которых выполняется соотношение Хагена - Пуазейля. Для большей корректности измерений магистрали подбирались строго прямыми, без изгибов, которые могли бы исказить полученные результаты.

Результаты и их обсуждение. В таблицах 1 и 2 приводятся экспериментальные и расчетные данные для трубок сечением 3 и 1,5 мм соответственно.

Таблица 1

Основные параметры течения жидкости по горизонтальной трубке диаметром 3,0 мм

l , м	l d	Re	Q 3 , мл/с
			Эксп.	Расч.
3,00	1000	1147	2,7±0,1	2,6
2,80	933	1190	2,8±0,1	2,8
2,60	867	1232	2,9±0,1	3,0
2,40	800	1275	3,0±0,1	3,3

2,20	733	1360	3,3±0,1	3,6
2,00	667	1445	3,5±0,1	3,9
1,80	600	1615	3,9±0,2	4,4
1,60	533	1742	4,4±0,2	4,9
1,40	467	1912	4,9±0,2	5,6
1,20	400	2125	5,5±0,2	6,6
1,00	333	2380	6,0±0,2	7,9
0,80	267	2847	6,6±0,2	9,9
0,60	200	3272	7,7±0,3	13,2
0,40	133	3867	9,1±0,3	19,7
0,20	67	4717	9,9±0,4	39,5

Таблица 2

Основные параметры течения жидкости по горизонтальной трубке диаметром 1,5 мм

l , м	l d	Re	Q 1,5 , мл/с
			Эксп.	Расч.
3,00	2000	102	0,17±0,01	0,17
2,80	1867	144	0,17±0,01	0,18
2,60	1733	153	0,18±0,01	0,19
2,40	1600	161	0,19±0,01	0,2
2,20	1467	178	0,21±0,01	0,22
2,00	1333	195	0,23±0,01	0,24
1,80	1200	255	0,26±0,01	0,27
1,60	1067	297	0,30±0,02	0,31
1,40	933	331	0,36±0,02	0,35
1,20	800	374	0,43±0,02	0,41
1,00	667	416	0,52±0,03	0,49
0,80	533	493	0,64±0,04	0,61
0,60	400	586	0,79±0,05	0,82
0,40	267	646	0,99±0,06	1,22
0,20	133	850	1,30±0,08	2,45

В первых колонках таблиц указаны длины трубок l в метрах; во вторых колонках – отношения длин трубок к их диаметрам _d ^l ; в третьих колонках – соответствующие им значения числа Рейнольдса Re ; в четвертых колонках – экспериментальные данные объемной скорости течения жидкости для трубок разной длины в мл/с: Q ₃ – для трубок диаметром 3 мм и Q _1,5 - для трубок диаметром 1,5 мм; в пятых колонках – соответствующие им значения объемной скорости течения жидкости, рассчитанные по формуле Пуазейля. Числа Рейнольдса рассчитывались по формуле

Re = ^{ρυ d} ,                                                  (2)

η где ρ - плотность жидкости, υ - линейная скорость течения жидкости, η - ее вязкость, d - диаметр трубки.

Как видно из таблицы 1, экспериментальные и расчетные данные объемной скорости течения жидкости для трубок диаметром 3 мм находятся в удовлетворительном согласии для значений числа Рейнольдса, не превышающих критическое Re = 2300. То же можно сказать и о данных, приведенных в таблице 2 для трубок диаметром 1,5 мм, для которых число Рейнольдса во всех случаях не достигает критического значения. Исключение составляют данные, полученные для трубок малых длин (0,2 – 0,4 м), при которых поток жидкости еще не успевает установиться.

Критерий l ≥ 500 , о котором говорится в работе [10], связан с критерием Рейнольдса, однако не может d быть объективным показателем характера движения жидкости, а, следовательно, и условием применимости формулы Хагена - Пуазейля. Об этом свидетельствуют то, что расчетные значения объемной скорости течения жидкости, полученные по этой формуле для случаев, когда l p 500 , также дают удовлетворительное согласие с d экспериментальными данными. Так, для трубки диаметром d = 3 мм и длиной l = 1,4 м ( l = 467 ) объемная d скорость течения жидкости, полученная экспериментально, составляя 4,9 мл/с, согласуется с расчетным значе- нием 5,6 мл/с. Аналогичное имеет место для трубки того же диаметра длиной 1,2 м (— = 400), при которых экс-d периментальное и расчетное значение составляют 5,5 и 6,6 мл/с соответственно.

Важным следствием формулы Хагена - Пуазейля является то, что при изменении диаметра трубки в 2 раза объемная скорость течения жидкости изменяется в 16 раз. Однако, авторы работы [10] указывают на обнаруженное ими нарушение этого критерия, приводя данные о том, что на самом деле Q при изменении d в 2 раза изменяется в 6 раз, а не в 16 раз, как это следует из формулы Хагена - Пуазейля. Эти данные находятся в полном противоречии с полученными нами экспериментальными данными. Как следует из таблицы 3, отношение ^{Q 3} для значений числа Рейнольдса, не превышающих критического, лежит в интервалах значений приблизи- Q 1,5

тельно от 13 до 16, что для условий эксперимента, в котором использовалась реальная жидкость, является результатом, находящимся в удовлетворительном согласии со следствием из формулы Хагена – Пуазейля.

Таблица 3

Сравнительный анализ параметров течения жидкости для трубок различных диаметров

l, м	d = 3 мм		d = 1,5 мм		Q 3 Q 1,5
	Q 3 , мл/с	Re	Q 1,5 , мл/с	Re
3,00	2,7±0,1	1147	0,17±0,01	102	15,9
2,80	2,8±0,1	1190	0,17±0,01	144	16,5
2,60	2,9±0,1	1232	0,18±0,01	153	15,8
2,40	3,0±0,1	1275	0,19±0,01	161	15,8
2,20	3,3±0,1	1360	0,21±0,01	178	15,7
2,00	3,5±0,1	1445	0,23±0,01	195	15,2
1,80	3,9±0,2	1615	0,26±0,01	255	15,0
1,60	4,4±0,2	1742	0,30±0,02	297	14,7
1,40	4,9±0,2	1912	0,36±0,02	331	13,6
1,20	5,5±0,2	2125	0,43±0,02	374	12,8
1,00	6,0±0,2	2380	0,52±0,03	416	11,5
0,80	6,6±0,2	2847	0,64±0,04	493	10,3
0,60	7,7±0,3	3272	0,79±0,05	586	9,7
0,40	9,1±0,3	3867	0,99±0,06	646	9,2
0,20	9,9±0,4	4717	1,30±0,08	850	7,6

На наш взгляд, результаты, приведенные в работе [10], были получены с нарушением условий, для которых была получена формула Хагена – Пуазейля, которая справедлива для жестких, прямых, горизонтальных трубок, ламинарного потока, гомогенной жидкости, смачиваемых поверхностей сосудов (трубок). Нарушение любого из этих условий может привести к расхождениям между экспериментальными и расчетными данными. Покажем это на следующем примере.

Оценим время истечения жидкости из расположенного вертикально сосуда цилиндрической формы диаметром D через канюлю диаметром d . Пусть и , - скорость понижения уровня жидкости в сосуде, и ₂ - скорость истечения жидкости через канюлю, соединенную с сосудом через отверстие в его дне. Считая жидкость идеальной, для нее можно записать уравнение Бернулли в следующем виде:

+ P gh =                                                   (3)

где р - плотность жидкости, h - ее высота в сосуде в данный момент времени, g - ускорение свободного паде- ния.

Решая (3) совместно с условием неразрывности струи и,5, = и252, где 5, и 52 - площади поперечного сече ния сосуда и канюли соответственно, можно определить и,:

^и ,

S 2 2 gh

V ⁵ 12 - ⁵ 2 2

Переходя в (4) от сечений S ₁ и S ₂ к диаметрам D и d , получим:

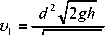
' D ⁴ - d ⁴

Учитывая, что d ⁴ pp D ⁴ , (5) можно переписать:

^и 1

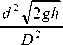
Вводя в (6) вместо h переменную координату уровня жидкости y , можно записать выражение для пони- жения уровня жидкости dy за малый промежуток времени dt :

dy =

D ²

dt .

Выражение (7) представляет собой дифференциальное уравнение с разделяющимися переменными, после решения которого получим время истечения жидкости из сосуда через канюлю:

1 2 h ( D ⁴ - d ⁴)' gd ⁴

которое при условии d ⁴ pp D ⁴ окончательно запишется:

t =

f D ) ² ^L I d J V g

Из (9) следует, что при увеличении диаметра канюли в 2 раза время истечения жидкости из сосуда уменьшится в 4 раза; соответственно в 4 раза увеличится объемная скорость истечения жидкости.

Таким образом, нельзя утверждать, что критерий справедливости формулы Хагена-Пуазейля — > 500 одно- d значен и соблюдается для трубок всех диаметров. Ведь в эксперименте, проводившемся в [10], канюли и пакет с жидкостью располагались не горизонтально, а разность давлений на концах трубки не поддерживалась постоянной.

Выводы.

• 1.    Несмотря на указанные противоречия, нельзя согласиться с выводами в [10], о том, что формула Хагена -Пуазейля ошибочна. Корректнее будет говорить о границах и условиях применимости формулы Хагена - Пуа-зейля.

• 2.    Модели, связывающие параметры движения жидкостей по цилиндрическим трубкам, справедливы для жестких трубок, ламинарного потока, гомогенной жидкости, смачиваемых поверхностей трубок. Все эти свойства не соответствуют системе кровообращения, в которой кровеносные сосуды являются эластическими структурами с турбулентными пульсирующими потоками негомогенной крови. Тем не менее, уравнение Хагена – Пуазейля может использоваться в гемодинамике как приближенное отображение реальности. В частности, существуют показатели кровообращения, полученные на основе этих уравнений.

• 3.    Объективным критерием применимости формулы Хагена - Пуазейля следует считать не значения величины _d ^l , на которую указывается в [10], а значения числа Рейнольдса, устанавливающего границу между ламинарным и турбулентным потоками жидкости. При значениях числа Рейнольдса, меньших его критического значения, формула Хагена – Пуазейля дает удовлетворительное согласие с экспериментом, что делает ее применение для описания кровообращения допустимым.

• 4.    Полученные данные могут быть полезными при оценке показателей кровообращения щитовидной железы при тиреоидной патологии. Кроме того, изучение кровотока в динамике на фоне проводимой заместительной и тиреостатической терапии при гипо- и гипертиреозе будет способствовать улучшению диагностики, назначению адекватной терапии и контролю её эффективности.