Чувствительность функционала эффективности процесса биологической очистки сточных вод к параметрам модели динамики концентраций биогенов
Автор: Е. С. Жменя, Н. С. Бузало
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1 (92) т. 18, 2018 года.
Бесплатный доступ
Статья посвящена вопросу анализа чувствительности функционала качества воды к параметрам модели искусственной водной экосистемы биологической очистки сточных вод, сформулированной в виде начальнокраевой задачи для системы уравнений реакции конвекции-диффузии, описывающей динамику биогенов. Использование многомерных нестационарных моделей водных экосистем с подробным описанием биохимических реакций осложняется большим числом параметров, значение которых необходимо получать экспериментально. Для упрощения процесса обеспечения данных была исследована чувствительность функционала качества очистки к параметрам модели.
Анализ чувствительности, много-параметрическая модель, теория малых возмуще- ний, сопряжённые уравнения, экосистема, очистка сточных вод, оптимизационная модель, управление экологическими системами, аэротенк-вытеснитель, функционал
Короткий адрес: https://sciup.org/142211874
IDR: 142211874 | УДК: 519.6 | DOI: 10.23947/1992-5980-2018-18-1-85-91
Текст научной статьи Чувствительность функционала эффективности процесса биологической очистки сточных вод к параметрам модели динамики концентраций биогенов
Введение. Рассматривается задача оптимального управления процессом биологической очистки сточных вод на основе математической модели, описывающей динамику концентраций биогенов в очистном сооружении. При решении задач управления экологическими системами на основе сложных многомерных и нестационарных моделей с подробным описанием биохимических реакций возникают сложности, связанные с большим числом параметров, значение которых необходимо получать экспериментально [1]. Для упрощения процесса обеспечения входных данных многопараметрической модели авторами исследуется чувствительность выбранной значимой скалярной характеристики (функционала качества очистки сточных вод, формирующего ограничение на переменную состояния в задаче оптимального управления) к параметрам модели. Путём этого исследования параметры можно разделить на наиболее значимые, для определения которых рекомендовано проведение натурных экспериментов, и наименее значимые, значения которых могут быть взяты приближённо.
Наиболее простым способом оценки чувствительности функционала к изменениям параметров многопараметрической модели является метод стохастического анализа (как линейного, так и нелинейного) [2–4]. Кроме этого, возможно применить метод, основанный на теории малых возмущений и сопряжённых уравнений [2, 5–7]. С вычислительной точки зрения этот алгоритм имеет преимущества по сравнению с прямыми методами, так как вместо многократного решения уравнений для множества параметров модели при расчёте компонентов градиента функционала предполагается одноразовое решение прямой и сопряжённой задач и вычисление интегралов, характеризующих оценку влияния изменения параметров к функционалу.
Данный подход реализован авторами в настоящей работе. Применение алгоритма оценки чувствительности, сформулированного ниже, возможно для любых процессов, связанных с массопереносом реагирующих веществ, таких как решение обратных источниковых задач динамики и кинетики газовых примесей и аэрозолей в атмосфере, моделирование биологических процессов в живых организмах, управление процессами массопереноса в аппаратах химических технологий и т. д. Возможно применять данный подход и для других классов задач.
Описание метода и алгоритма. Рассматривается задача, описывающая распространение и массоперенос неконсервативных примесей, представляющая собой краевую задачу для полулинейной системы уравнений реак-ции-конвекции-диффузии:
д S — + д t
div (и • S )-AS = Q (S, X),
где S — вектор концентраций примесей, S = {Si-}, i = 1, M ; Q (S, X) — вектор-функция, описывающая источники и реакции между примесями; и — вектор скорости течения среды; X — вектор параметров X = {Xl}, l = 1, L, где
3 д I д ... ]
L
число параметров; A — оператор диффузионного переноса: A... = ^ — II k + kx )—I, где i=1 дxi (v -/ дxi)
( x 1 ,x 2 ,x3) ^ ( x , y , z ) — пространственные координаты, k + k x — сумма коэффициентов молекулярной и турбулентной диффузии (в направлении x i ) соответственно.
Пусть имеется некоторый интересующий нас функционал:
J = { Р, S), где знак {,) обозначает скалярное произведение в области Txfi (T: {te[t0, T]}, fi — пространственная расчётная область), т. е. (г, h = J r (x) h (x)dfidt, здесь r(x), h(x) — некоторые произвольные функции, заданные в обла-Txfi сти Txfi; р = {pi} — вектор функция, i-й элемент которой равен 1 в значимых по веществу i зонах fii и равен 0 в остальной области, т. е.:
-
1 при x e fi i x T , 0 при x й fi i x T .
Вдали от точек бифуркации решения системы (1) малые изменения параметров порождают возмущённую задачу, решение которой можно представить в виде ряда:
, l д S ( t , Х )
S (t, Х) = S (t, х) + £ 5Х(1), где дХ(1) — вариации параметров, дХ = Х-Х = {дХ( 1)}.
Функция чувствительности по l- му параметру
д S ( t , х ) дХ ( 11
, является решением системы уравнений модели
( t , х ) :
(1), линеаризованной относительно невозмущённой траектории S = S
, , =х =х дs (t, х) ^(s(t,х),Х^ ' ' =-Q .
дХ ( 1 1 дХ ( 11
Оператор
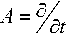
. * ГдQ/ ■
+ div -Л- % S
задаёт систему уравнений линейного приближения, где запись [ ■ ] обозначает матрицы частных производных правой части системы. Первая вариация функционала определяется по формуле:
3J1 =(5S, р) = (®,5Q), I = i^L, (4)
где ю — решение задачи с оператором A , сопряжённым к A .
Определение вариации функционала (4) в рамках прямого подхода предполагает расчёт функций чувствительности, а для многопараметрической модели — многократное решение начальной задачи для системы уравнений (3). Использование решения сопряжённой задачи A* позволяет вместо многократного решения уравнений линейного приближения для множества параметров основной задачи при расчёте компонентов градиента функционала J реализовать подход, который предполагает одноразовое решение прямой и сопряжённой задачи и нахождения скалярного произведения:
д J
дХ 1
д Q
Ю,--т дх( 11
1 = 1, L .
Алгоритм оценки чувствительности функционала к изменениям параметров моделей при помощи теории малых возмущений и сопряжённых уравнений предполагает выполнение следующих этапов:
-
1. линеаризация полулинейной системы уравнений реакции-конвекции-диффузии (1);
-
2. формулировка задачи, сопряжённой к линеаризованной;
-
3. нахождение решения прямых и сопряжённых задач;
-
4. вычисление скалярного произведения (5) для каждого параметра Х 1 , 1 = 1, L ;
-
5. оценка полученных компонент градиента функционала. Чем больше соответствующая компонента, тем большее влияние оказывает изменение параметра Х 1 на функционал.
Информатика, вычислительная техника и управление
Постановка задачи управления биологической очисткой сточных вод и результаты численных экспериментов. Определим влияние вариации различных параметров модели экосистемы аэротенка-вытеснителя на функционал, характеризующий эффективность процесса очистки сточных вод от загрязняющих веществ. Под аэротенком-вытеснителем здесь понимается элемент очистного сооружения, в котором воды, загрязнённые аммонийным азотом ( N ), являющимся наиболее опасным для организма человека веществом, смешиваются с активным илом ( A ), а также аэрируются кислородом ( OX ), необходимым для протекания биохимических реакций. В ходе прохождения «смеси» по аэротенку происходит очищение сточных вод от загрязняющего вещества в процессе наращивания биомассы активного ила [8, 9]. Схема аэротенка-вытеснителя изобра-
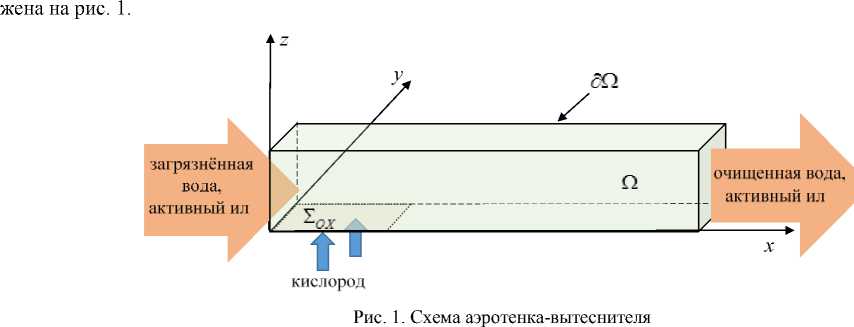
Fig. 1. Scheme of aeration tank
Сформулируем задачу оптимального управления аэрацией элемента очистного сооружения.
Управлением является мощность источника кислорода F OX ( t ) . Функция цели задачи обеспечивает минимизацию затрат на поступление кислорода в водную систему аэротенка-вытеснителя в течении периода времени T:
T
/Е .Fox (t) dt ^ min, t 0
где Et — затраты, необходимые для подачи кислорода объёмом FOX (t) на единицу площади источника в мо- мент времени t = 10, T .
Переменными состояния задачи являются концентрации N, A и OX: —N, —A, —OX . Оптимизационная модель включает в себя следующее ограничение на переменную состояния:
( p N ( x ) , SN SN , PDK ) — 0 , x 5 Q ,
где SN PDK — предельно допустимая концентрация аммонийного азота; pN ( x ) — функция типа (2), характеризующая значимую область (соответствует зонам водозабора из сооружения).
Управление удовлетворяет ограничению на знак:
Fox (t )> 0, t=t^.
Решение задачи оптимизации должно удовлетворять краевой задаче, описывающей массоперенос и трансформацию неконсервативных примесей (уравнениям состояния):
^ + div (u ■ Sa )-AS a =
—Ф A — A 2
- l A S A ,
^ + div (u ■ — n ) —ASN =5 N-a dt
d — OX - + div ( u ■ — OX ) — A — OX
H m S N у 2 KN + S N + -N- NN in
KN
■
K OX
S OX
— —A —
OX
—
t = t 0, T , x eQ ,
----H m-N 2 - a , t = t 0 , T , x eQ , K, + - v + - N
NN in KN
—
H m — OX
OX + OX
— a , t = 1 0 , T , x eQ ;
d S. . _ _ —— _
= 0, i = { A , N , OX } , x edQ , t = t 0 , T , x £S OX ;
^ — - = OX — k ox F ox ( t ) , t — 1 0 , T , x . ^ OX ; d N
- i — -“ , i = { A,N , OX } , x eQ , t — 1 0 .
В вышеприведенных уравнениях ц m — максимальная скорость роста активного ила; K i , i = { A, N , OX } — константы полунасыщения; Kl” , i = { A, N , OX } — константы ингибирования роста активного ила; ф A — коэффициент внутривидовой конкуренции; lA — скорость отмирания; 5 N — скорость выделения аммонийного азота в процессе жизнедеятельности активного ила; kOX — коэффициент, равный отношению скорости растворения кислорода к коэффициенту диффузии в направлении нормали N . Задача состоит в оценке чувствительности функционала из ограничения (6) к параметрам модели.
Для реализации изложенного выше алгоритма необходимо сформулировать задачу нахождения вектора ю ( t ) = ( - A ( t ) , - N ( t ) , - O x ( t ) ) T , то есть сопряжённую к краевой задаче [10], являющейся линейным приближением к задаче (7)-(12).
Сопряжённая задача имеет вид:
d - A
—
d t
div - A + А S A
—
—P m-N -2 K -OX^ "2фA-A — lA K n + S n + S^ OX + OX
S A —
—
з N
—
P m - N ----2 -- X K, , + SM + -N—
<г* J. I p m S OX I c*
S x / + ---- S — 0,
N I I OX .
v K OX + S OX J
d S N
—
d t
div Sn + АSn —
—
P m S OX S A
—
—
P m - A
v
---I
Ц„ -n-ox- 1 + N m N OX A in
K
nm ( K OX + S OX ) Km
----2
S N
IA
P -N-. 1 + —N " m N Ainm
KN
+---T
----2
S N
*
S
----2
S N
= P n ,
S A —
( K ox + S ox )
---O ^ — div - OX + А - o X — d t
P m - N - A
P m - N - ox - A
K in ( K OX + S OX )
Km
-., / ----- \2
"TZ in - ( K OX + S OX ) K
s a —
P m - A , P m - Ox - A
( K OX + - OX ) ( K OX + - OX )
*
SOX
— 0;
Информатика, вычислительная техника и управление
uNS * + = 0, i = { A,N , OX } , x eSQ , t = t 0, T , x C^ox,
N I NJ^ О OX
S * = 0, i = { A, N , OX } , x eQ , t = 1 0.
В системе (13)-(17) S i , i = { A, N , OX } — среднее значение концентрации, полученное при решении системы (7)-(12) с невозмущёнными параметрами.
Далее определим чувствительность функционала из ограничения (6) к изменениям следующих параметров X l : K i , i = { N , OX } ; K™ ; 5 N ; 1 a ; ф A ; ц m . Результаты вычисления скалярных произведений (5) сведены в таблицу 1.
Таблица 1
Table 1
Чувствительность функционала эффективности процесса биологической очистки
Efficiency functional sensitivity of biological purification
|
Коэффициенты |
дJ/ 7 = 17 /ЭХ l ’ 1 1,7 |
Коэффициенты |
d J/ z = 1 у / ЭХ l ’ 1 1,7 |
|
K OX |
1,75 |
1 a |
-2,01 |
|
K n |
0,96 |
Ф A |
-1,69 |
|
ц m |
0,87 |
5 N |
-0,0001 |
|
in K N |
0,003 |
Обсуждение и заключения. Анализ чувствительности функционала показал, что параметры, характеризующие константу полунасыщения по кислороду ( KOX ), константу полунасыщения по аммонийному азоту ( K N ), максимальную скорость роста активного ила ( ц m ), скорость отмирания активного ила ( lA ) и коэффициент внутривидовой конкуренции ( ф A ) оказывают наибольшее влияние на вариацию функционала эффективности очистки сточных вод и их значения следует определять экспериментально. В тоже время изменения параметров, характеризующих константу ингибирования роста активного ила ( K N ) и скорость выделения аммонийного азота в процессе жизнедеятельности активного ила ( 5 N ) практически не влияют на изменение функционала, характеризующего эффективность очистки сточных вод, и, следовательно, при расчетах можно использовать средние значения этих параметров.


