Чувствительность функционала эффективности процесса биологической очистки сточных вод к параметрам модели динамики концентраций биогенов

Введение. Рассматривается задача оптимального управления процессом биологической очистки сточных вод на основе математической модели, описывающей динамику концентраций биогенов в очистном сооружении. При решении задач управления экологическими системами на основе сложных многомерных и нестационарных моделей с подробным описанием биохимических реакций возникают сложности, связанные с большим числом параметров, значение которых необходимо получать экспериментально [1]. Для упрощения процесса обеспечения входных данных многопараметрической модели авторами исследуется чувствительность выбранной значимой скалярной характеристики (функционала качества очистки сточных вод, формирующего ограничение на переменную состояния в задаче оптимального управления) к параметрам модели. Путём этого исследования параметры можно разделить на наиболее значимые, для определения которых рекомендовано проведение натурных экспериментов, и наименее значимые, значения которых могут быть взяты приближённо.

Наиболее простым способом оценки чувствительности функционала к изменениям параметров многопараметрической модели является метод стохастического анализа (как линейного, так и нелинейного) [2–4]. Кроме этого, возможно применить метод, основанный на теории малых возмущений и сопряжённых уравнений [2, 5–7]. С вычислительной точки зрения этот алгоритм имеет преимущества по сравнению с прямыми методами, так как вместо многократного решения уравнений для множества параметров модели при расчёте компонентов градиента функционала предполагается одноразовое решение прямой и сопряжённой задач и вычисление интегралов, характеризующих оценку влияния изменения параметров к функционалу.

Данный подход реализован авторами в настоящей работе. Применение алгоритма оценки чувствительности, сформулированного ниже, возможно для любых процессов, связанных с массопереносом реагирующих веществ, таких как решение обратных источниковых задач динамики и кинетики газовых примесей и аэрозолей в атмосфере, моделирование биологических процессов в живых организмах, управление процессами массопереноса в аппаратах химических технологий и т. д. Возможно применять данный подход и для других классов задач.

Описание метода и алгоритма. Рассматривается задача, описывающая распространение и массоперенос неконсервативных примесей, представляющая собой краевую задачу для полулинейной системы уравнений реак-ции-конвекции-диффузии:

д S — + д t

div (и • S )-AS = Q (S, X),

где S — вектор концентраций примесей, S = {Si-}, i = 1, M ; Q (S, X) — вектор-функция, описывающая источники и реакции между примесями; и — вектор скорости течения среды; X — вектор параметров X = {Xl}, l = 1, L, где

3 ^д I               ^д ... ]

L

число параметров; A — оператор диффузионного переноса:   A... = ^ — II k + kx )—I, где i=1 дxi (v -/ дxi)

( x 1 ,x 2 ,x₃) ^ ( x , y , z ) — пространственные координаты, k + k x — сумма коэффициентов молекулярной и турбулентной диффузии (в направлении x i ) соответственно.

Пусть имеется некоторый интересующий нас функционал:

J = { Р, S), где знак {,) обозначает скалярное произведение в области Txfi (T: {te[t0, T]}, fi — пространственная расчётная область), т. е. (г, h = J r (x) h (x)dfidt, здесь r(x), h(x) — некоторые произвольные функции, заданные в обла-Txfi сти Txfi; р = {pi} — вектор функция, i-й элемент которой равен 1 в значимых по веществу i зонах fii и равен 0 в остальной области, т. е.:

• 1    при x e fi i x T , 0 при x й fi i x T .

  
  

Вдали от точек бифуркации решения системы (1) малые изменения параметров порождают возмущённую задачу, решение которой можно представить в виде ряда:

, l д S ( t , Х )

S (t, Х) = S (t, х) + £          5Х(1), где дХ(1) — вариации параметров, дХ = Х-Х = {дХ( 1)}.

Функция чувствительности по l- му параметру

д S ( t , х ) дХ ^{( 11}

, является решением системы уравнений модели

⁽ t , ^{х )} :

(1), линеаризованной относительно невозмущённой траектории S = S

, , =х =х дs (t, х) ^(s(t,х),Х^   '    ' =-Q .

дХ ^{( 1 1}       дХ ^{( 11}

Оператор

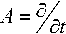
.        * ГдQ/ ■

^{+ div -Л-} % S

задаёт систему уравнений линейного приближения, где запись [ ■ ] обозначает матрицы частных производных правой части системы. Первая вариация функционала определяется по формуле:

3J1 =(5S, р) = (®,5Q), I = i^L,                                              (4)

где ю — решение задачи с оператором A , сопряжённым к A .

Определение вариации функционала (4) в рамках прямого подхода предполагает расчёт функций чувствительности, а для многопараметрической модели — многократное решение начальной задачи для системы уравнений (3). Использование решения сопряжённой задачи A* позволяет вместо многократного решения уравнений линейного приближения для множества параметров основной задачи при расчёте компонентов градиента функционала J реализовать подход, который предполагает одноразовое решение прямой и сопряжённой задачи и нахождения скалярного произведения:

д J

дХ 1

д Q

Ю,--т дх( 11

1 = 1, L .

Алгоритм оценки чувствительности функционала к изменениям параметров моделей при помощи теории малых возмущений и сопряжённых уравнений предполагает выполнение следующих этапов:

• 1.    линеаризация полулинейной системы уравнений реакции-конвекции-диффузии (1);

• 2.    формулировка задачи, сопряжённой к линеаризованной;

• 3.    нахождение решения прямых и сопряжённых задач;

• 4.    вычисление скалярного произведения (5) для каждого параметра Х ¹ , 1 = 1, L ;

• 5.    оценка полученных компонент градиента функционала. Чем больше соответствующая компонента, тем большее влияние оказывает изменение параметра Х 1 на функционал.

  Информатика, вычислительная техника и управление

  
  

Постановка задачи управления биологической очисткой сточных вод и результаты численных экспериментов. Определим влияние вариации различных параметров модели экосистемы аэротенка-вытеснителя на функционал, характеризующий эффективность процесса очистки сточных вод от загрязняющих веществ. Под аэротенком-вытеснителем здесь понимается элемент очистного сооружения, в котором воды, загрязнённые аммонийным азотом ( N ), являющимся наиболее опасным для организма человека веществом, смешиваются с активным илом ( A ), а также аэрируются кислородом ( OX ), необходимым для протекания биохимических реакций. В ходе прохождения «смеси» по аэротенку происходит очищение сточных вод от загрязняющего вещества в процессе наращивания биомассы активного ила [8, 9]. Схема аэротенка-вытеснителя изобра-

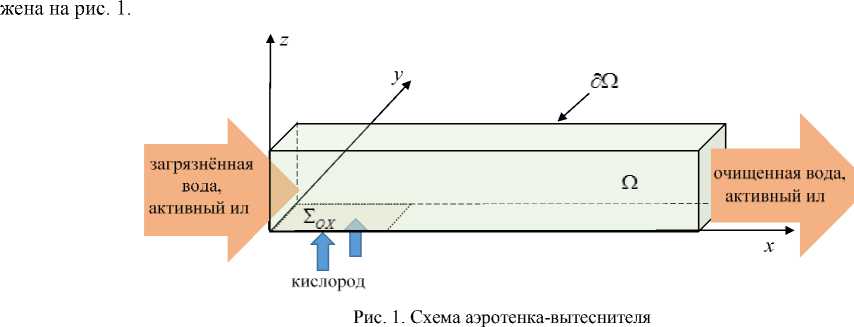
Fig. 1. Scheme of aeration tank

Сформулируем задачу оптимального управления аэрацией элемента очистного сооружения.

Управлением является мощность источника кислорода F OX ( t ) . Функция цели задачи обеспечивает минимизацию затрат на поступление кислорода в водную систему аэротенка-вытеснителя в течении периода времени T:

T

/Е .Fox (t) dt ^ min, t 0

где Et — затраты, необходимые для подачи кислорода объёмом FOX (t) на единицу площади источника в мо- мент времени t = 10, T .

Переменными состояния задачи являются концентрации N, A и OX: —N,  —A, —OX . Оптимизационная модель включает в себя следующее ограничение на переменную состояния:

( p N ⁽ x ) , ^SN ^SN , PDK ) — ⁰ , x ^{5 Q} ,

где S_{N PDK} — предельно допустимая концентрация аммонийного азота; p_N ( x ) — функция типа (2), характеризующая значимую область (соответствует зонам водозабора из сооружения).

Управление удовлетворяет ограничению на знак:

Fox (t )> 0, t=t^.

Решение задачи оптимизации должно удовлетворять краевой задаче, описывающей массоперенос и трансформацию неконсервативных примесей (уравнениям состояния):

^ + div (u ■ Sa )-AS a =

—Ф A — A ²

- l A ^S A ,

^ + div (u ■ — n ) —ASN =5 N-a dt

^{d — OX} - + div ( u ■ ^— OX ) ^{— A —} OX

H m S N у ² K_N + S _N + -N- NN in

KN

■

^K OX

S OX

— ^—A ^—

OX

—

t = t ₀, T , x eQ ,

----^{H m-N}   2 - a , t = t 0 , T ,   x eQ , K, + - v + ^{- N}

NN in K_N

—

H m ^— OX

OX ⁺ OX

— a , t = 1 0 , T , x eQ ;

d S.          .                 _ _      ——      _

= 0, i = { A , N , OX } , x edQ , t = t ₀ , T , x £S _OX ;

^ — - = OX — k ox F ox ( t ) , t — 1 0 , T , x . ^ OX ; d N

- i — -“ , i = { A,N , OX } , x eQ , t — 1 ₀ .

В вышеприведенных уравнениях ц m — максимальная скорость роста активного ила; K i , i = { A, N , OX } — константы полунасыщения; K^l” , i = { A, N , OX } — константы ингибирования роста активного ила; ф A — коэффициент внутривидовой конкуренции; l_A — скорость отмирания; 5 N — скорость выделения аммонийного азота в процессе жизнедеятельности активного ила; k_OX — коэффициент, равный отношению скорости растворения кислорода к коэффициенту диффузии в направлении нормали N . Задача состоит в оценке чувствительности функционала из ограничения (6) к параметрам модели.

Для реализации изложенного выше алгоритма необходимо сформулировать задачу нахождения вектора ю ( t ) = ( - A ( t ) , - N ( t ) , - O _x ( t ) ) T , то есть сопряжённую к краевой задаче [10], являющейся линейным приближением к задаче (7)-(12).

Сопряжённая задача имеет вид:

d - A

—

d t

div - A + А S A

—

—^P m^-N -2 K ^-OX^ "^2фA-A — lA K n + S n + S^ O^{X +} O^X

S A —

—

з N

—

P m - N ----2 -- X K, , + S_M + -N—

<г* J. I    ^p m S ^OX    I c*

S x / +         ---- S — 0,

^N I                     I ^OX .

v ^K OX ⁺ S OX J

d S N

—

d t

div Sn + АSn —

—

^P m ^S OX ^S A

—

—

P m - A

v

---I

Ц„ -n-ox-  1 + N m N OX A        in

K

nm ( ^K OX + ^S OX ) Km

----2

S N

IA

P -N-. 1 + —N " m N Ainm

KN

+---T

----2

S N

*

S

----2

S N

= P n ,

S A —

( K ox + S ox )

---O ^ ^{— div -} OX + ^{А -} o X ^— d t

P m - N - A

P m - N - ox - A

_K in ( K OX ⁺ S OX )

Km

-.,     /          ----- \2

"TZ in ^- ( K OX ⁺ S OX ) K

s a —

P m - A    ,    P m - Ox - A

⁽ K ^{OX + - OX} ) ( K OX ^{+ -} OX )

*

SOX

— 0;

Информатика, вычислительная техника и управление

u_NS * +    = 0, i = { A,N , OX } , x eSQ , t = t ₀, T , x C^_ox,

N I     NJ^                                            О             OX

S * = 0, i = { A, N , OX } , x eQ , t = 1 ₀.

В системе (13)-(17) S i , i = { A, N , OX } — среднее значение концентрации, полученное при решении системы (7)-(12) с невозмущёнными параметрами.

Далее определим чувствительность функционала из ограничения (6) к изменениям следующих параметров X _l : K i , i = { N , OX } ; K™ ; 5 N ; 1 a ; ф A ; ц m . Результаты вычисления скалярных произведений (5) сведены в таблицу 1.

Таблица 1

Table 1

Чувствительность функционала эффективности процесса биологической очистки

Efficiency functional sensitivity of biological purification

Коэффициенты	дJ/   7 = 17 /ЭХ l ’ 1   1,7	Коэффициенты	d J/    z = 1 у / ЭХ l ’ 1   1,7
K OX	1,75	1 a	-2,01
K n	0,96	Ф A	-1,69
ц m	0,87	5 N	-0,0001
in K N	0,003

Обсуждение и заключения. Анализ чувствительности функционала показал, что параметры, характеризующие константу полунасыщения по кислороду ( K_OX ), константу полунасыщения по аммонийному азоту ( K N ), максимальную скорость роста активного ила ( ц m ), скорость отмирания активного ила ( l_A ) и коэффициент внутривидовой конкуренции ( ф A ) оказывают наибольшее влияние на вариацию функционала эффективности очистки сточных вод и их значения следует определять экспериментально. В тоже время изменения параметров, характеризующих константу ингибирования роста активного ила ( K N ) и скорость выделения аммонийного азота в процессе жизнедеятельности активного ила ( 5 N ) практически не влияют на изменение функционала, характеризующего эффективность очистки сточных вод, и, следовательно, при расчетах можно использовать средние значения этих параметров.