Чувствительные элементы датчиков на дисперсионных линиях задержки

Первые работы по исследованию чувствительных элементов (ЧЭ) датчиков на поверхностных акустических волнах (ПАВ) были начаты в 1958 - 1960 гг. Наиболее технологичными оказались устройства, изготовленные на пьезоэлектрических монокристаллах (кварца, ниобата лития, танталата лития, германата висмута, лангаситов и т. д.) [1, 2].

Чувствительный элемент датчика на ПАВ представляет собой тонкую отполированную пластинку (например, кварцевую), на которую нанесены две системы встречно-штыревых преобразователей (ВШП), одна из которых работает в качестве передающего элемента — генератора ПАВ, а вторая является принимающим элементом — преобразователем ПАВ в выходное напряжение. Измеряемыми величинами ЧЭ являются: резонансная частота, на которую в процессе измерений настраивается частота подаваемого на резонатор напряжения, сдвиг фазы входного сигнала относительно выходного (время задержки), различные параметры сжатого сигнала в случае использования согласованной фильтрации. Датчики с такими ЧЭ способны измерять температуру, давление, механическую нагрузку, перемещения и передавать информацию как по проводам, так и беспроводным способом.

Существенным недостатком резонансных ЧЭ является их узкополосность (девиация частоты не превышает 0.1 %) и соответственно низкая помехозащищенность. Для повышения помехозащищенности в данной работе предлагается использовать специальные топологические решения на основе принципов согласованной фильтрации. В качестве наиболее простой реализации исследуется ЧЭ, реализующий в номинальном (невозмущенном) режиме сжатие линейно-частотно-моду-лированного (ЛЧМ) сигнала.

НОВЫЙ ПОДХОД К РАЗРАБОТКЕ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ НА ПАВ

Существующие в настоящее время ЧЭ на дисперсионных линиях задержки (ДЛЗ), т. е. реализующие метод согласованной фильтрации, в качестве информационной величины используют время задержки [1, 3]. Такой ЧЭ представляет собой дисперсионную линию задержки [3] и состоит из ВШП и расположенных на пьезоплате c одной стороны от ВШП дисперсионных отражающих структур в виде системы канавок с переменным периодом. В качестве информационного сигнала используется время задержки.

По сравнению с резонаторами и линиями задержки чувствительный элемент деформации с дисперсионными структурами имеет бóльшую чувствительность. Недостатком этих ЧЭ применительно к измерению деформаций является малая девиация частоты информационного сигнала и, как следствие, низкая чувствительность и точность, не превышающая 1 % в диапазоне действия внешних воздействующих факторов (ВВФ). Причиной этого является необходимость обеспечения постоянства распределения деформации по всей длине топологии датчика.

Предлагаемый новый подход к разработке чувствительных элементов на ПАВ заключается в создании ЧЭ, состоящего, как и прежде, из пьезоплаты, на поверхности которой сформированы не менее одного встречно-штыревого преобразователя и не менее одной дисперсионной отражающей структуры, но с каждой из двух сторон от ВШП. Информационный сигнал используется в форме частотно-модулированного зондирующего сигнала, обеспечивающей максимальное значение отклика по амплитуде чувствительного элемента деформации с дисперсионными структурами.

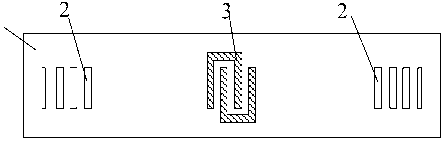
Рис. 1. Чувствительный элемент деформации с дисперсионными структурами

Расположение дисперсионных отражающих структур с двух сторон от ВШП позволяет реализовать при воздействии ВВФ нелинейную модуляцию импульсной переходной функции фильтра, например синусоидальную. Сущность предлагаемого подхода поясняется схемой на рис. 1, где приведены структура чувствительного элемента деформации с дисперсионными структурами. При деформации пьезоплаты 1 изменяется скорость распространения ПАВ, геометрический размер штырей (электродов) ВШП 3, расстояния между электродами, ширина и период следования канавок отражающих дисперсионных структур 2. В соответствии с этим изменяется время задержки отраженного сигнала и частотные свойства отражающих дисперсионных структур 2. Отражающие дисперсионные структуры 2 выполнены в виде периодической системы канавок с переменным периодом.

При поступлении зондирующего электрического сигнала от внешнего источника на ВШП 3 под действием пьезоэлектрического эффекта формируется ПАВ. Сформированная ВШП 3 ПАВ распространяется в двух направлениях от ВШП 3. Дойдя до отражающих дисперсионных структур 2 ПАВ отражается и возвращается на ВШП 3.

В качестве зондирующего сигнала при использовании дисперсионных структур наиболее часто используются частотно-модулированные сигналы, структура которых соответствует топологии отражающих дисперсионных структур 2 [1]. При изменении топологии отражающих дисперсионных структур 2 будет изменяться и структура соответствующих частотно-модулированных сигналов. Наиболее часто используются ЛЧМ-сигналы [1]. Взаимодействие зондирующего электрического ЛЧМ-сигнала с дисперсионными отражающими структурами подробно изложено в [1].

В случае, если деформация чувствительного элемента деформации с дисперсионными структурами в области расположения ВШП 3 и отражающих дисперсионных структур 2 происходит по нелинейному закону, то будет изменяться форма частотно-модулированного зондирующего сигнала, обеспечивающая максимальное значение от- клика по амплитуде чувствительного элемента деформации с дисперсионными структурами. При этом форма нелинейно-частотной модуляции для каждой деформации чувствительного элемента будет однозначной функцией деформации.

Другими словами, наличие ВВФ приводит к рассогласованию согласованного в номинальном режиме фильтра, реализованного на ДЛЗ. В статье предлагается согласованную фильтрацию восстанавливать выбором формы зондирующего сигнала, наиболее точно соответствующей форме импульсной переходной функции ДЛЗ, находящейся под воздействием ВВФ. Далее на основе градуировочной зависимости (форма—деформация) изменению формы предлагается соотносить величину деформации.

Требуемая форма сигнала может быть реализована двумя способами:

• 1)    формирование требуемого профиля мембраны для обеспечения расчетного распределения фазовых сдвигов;

• 2)    программное формирование зондирующего частотно-модулированного сигнала, соответствующего физически реализуемому фазовому сдвигу на мембране простейшей (например, плоской) формы.

В первом случае необходимо рассчитать профиль мембраны таким образом, чтобы реализовался требуемый закон изменения фазового сдвига, а сжатый линейно-частотно-модулированный сигнал имел наибольшую чувствительность к деформации.

Во втором случае для известных распределений деформации мембраны и скоростей ПАВ требуется подобрать такую форму частотно-модули-рованного сигнала, чтобы при фиксированной топологии отражающих структур и ВШП обеспечить наибольшую чувствительность сжатого сигнала к деформации и, в частности к атмосферному давлению.

МОДЕЛИРОВАНИЕ ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА ДАТЧИКА ДАВЛЕНИЯ

Основная форма конструктивного исполнения датчиков на ПАВ — бесконтактные (дистанционные) пассивные датчики. Это определяется с одной стороны высокими частотами (сотни и тысячи МГц), что облегчает решение проблемы приема и передачи радиосигналов, а с другой — высокой стоимостью аппаратуры обработки сигналов ПАВ-датчика. Однако в случае пассивных дистанционных датчиков оба указанные свойства не снижают экономической эффективности, т. к. приемопередатчики необходимы для любых дистанционных приложений, а сложность обработки компенсируется дешевизной процессоров.

Деформация поверхности мембраны приводит к изменению скорости распространения ПАВ и изменению линейных расстояний между элементами топологии ДЛЗ — ВШП и отражающих структур (ОС), что приводит к изменению импульсной переходной функции эквивалентного согласованного фильтра, используемого в качестве модели ДЛЗ, образованного ВШП и ОС.

Искажение импульсной переходной функции фильтра, вызванное деформацией, может быть смоделировано учетом дополнительного фазового сдвига, на который в математической модели должны быть наложены естественные ограничения:

• 1)    максимальные дополнительные изменения фазы, вызванные деформацией, не превышают 1 % от текущего номинального (неискаженного деформацией) значения фазы ПАВ;

• 2)    изменение фазы в направлении распространения ПАВ является монотонно возрастающей функцией времени и естественной координаты (пройденного ПАВ расстояния).

Далее математическая модель устройства определяется выбранной топологией ДЛЗ, срезом и типом материала мембраны.

Рассмотрим модель чувствительного элемента на ДЛЗ с односторонним расположением ОС относительно ВШП и реализуем в номинальном режиме линейно-частотно-модулированный (ЛЧМ) сигнал.

Импульсная переходная функция может быть представлена в виде y1(t)=cos(ω1t+k1t2), (1)

где ω ₁ — начальное значение круговой частоты, ω ₁ = 2 π f ₁; k ₁ — скорость изменения круговой

ω 2 - ω 1

частоты, k = 21, ω = 2π f ; (ω – ω ) — де-Tm виация круговой частоты; Tm — время существования сворачиваемых функций; f1 , f2 — начальные значения частот модуляции.

Согласованный с (1) ЛЧМ-сигнал:

y ₂( t ) = cos( ω ₂ t - k ₁ t ²).                  (2)

Сжатый выходной сигнал датчика:

t

S ( t ) = ∫ y ₁( t - τ ) y ₂( τ )d τ =

t

= ∫ cos[ ω ₁( t - τ ) + k ₁( t - τ )²] ×

× cos( ω ₂ τ - k ₁ τ ² +∆ ϕ ( τ ))d τ ,        (3)

где ∆ ϕ — дополнительное изменение фазы, вызванное деформацией мембраны.

Для двустороннего (относительно ВШП) расположения ОС может быть реализовано изменение дополнительной фазы (возмущающего сигнала) во времени, соответствующее синусоидальному закону

∆ ϕ ( τ ) = Fim ⋅ sin( k_s τ ^d ),                (4)

где Fim = 0.01( ωτ - k τ ²) ; k = ^{m 1} ; Fim 1 — максимальная величина набега ^m фазы; d = 2;

T_m = ^{4 ⋅ 103} = 4.619 ⋅ 10 ^{- 6}с; k ₁ = ^{ω 2}

-

^ω 1

; ω ₂ = 2 π f ₂;

т m

ω 1 = 2 π f 1 ; f 02 = 466МГц; f 01 = 400МГц.

На рис. 2 показана зависимость амплитуды сжатого сигнала от показателя степени дополнительного набега фазы (возмущающего сигнала), вызванного гармонической деформацией (4) при Fim1 = 24π (двенадцать периодов). Как следует из рис. 2, при значениях показателя степени d, находящихся в пределах d < 1.0, амплитуда сжатого сигнала уменьшается примерно в 8 раз.

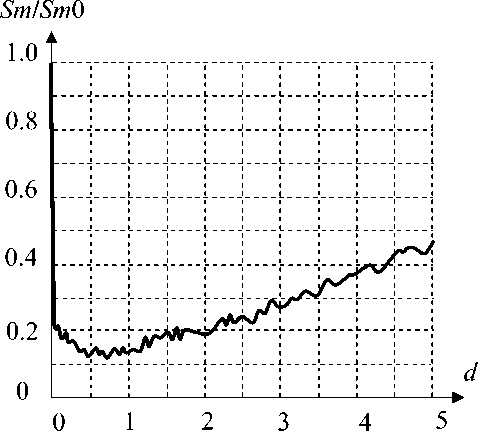
Рис. 2. Влияние показателя степени при формировании фазы возмущающего сигнала по синусоидальному закону.

Sm , Sm 0 — амплитуда возмущенного и невозмущенного сигналов соответственно; d — - показатель степени в формуле (4)

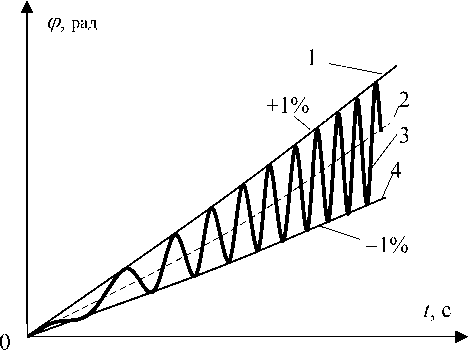
Рис. 4. Схема суммирования фаз.

1 — верхняя граница; 2 — номинальное значение; 3 — схема изменения фазы под действием синусоидального возмущения; 4 — нижняя граница

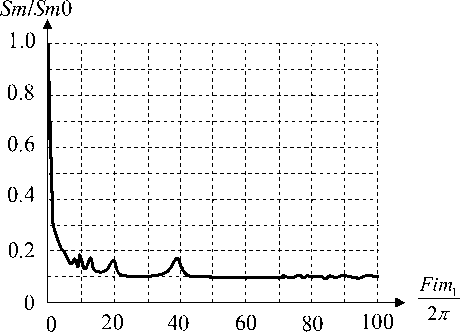
Рис. 3. Изменение амплитуды сжатого сигнала в зависимости от количества периодов.

Fim 1 — - максимальное изменение фазы возмущающего сигнала в формуле (4)

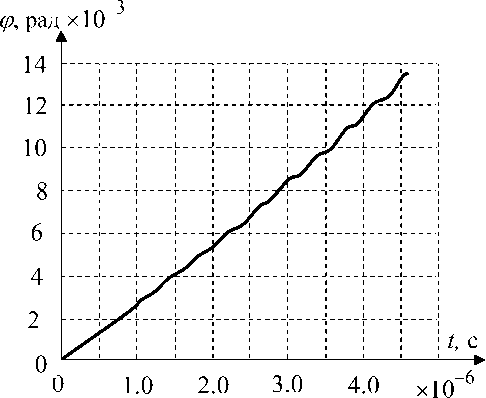
Рис. 5. Изменение суммарной фазы при 12-пери-одном изменении фазы возмущающего сигнала. ϕ — суммарная фаза; t — время

На рис. 3 при d = 1 приведена зависимость амплитуды сжатого сигнала от количества периодов, на которые синусоидально изменяется фаза возмущающего сигнала. Из рис. 3 следует, что при количестве периодов изменения фазы возмущающего сигнала, превышающем 42 периода, амплитуда сжатого сигнала остается на уровне 0.1 от номинального значения.

Все графики нормированы к максимальному значению амплитуды невозмущенного сжатого сигнала. Таким образом, периодическая модуляция фазы оказалась более эффективной, чем сте-пеннáя модуляция.

На рис. 4 показана схема изменения значений фазы при формировании фазы возмущающего сигнала по синусоидальному закону: 1 — верхняя граница (соответствует растяжению); 2 — номинальное значение (соответствует ЛЧМ); 3 — схема изменения фазы под действием синусоидального возмущения; 4 — нижняя граница.

На рис. 5 приведен график изменения суммарной фазы при изменении фазы возмущающего сигнала по синусоидальному закону (4) с параметрами: Fim 1 = 12 ⋅ 2 π = 75.3982 и d =1.

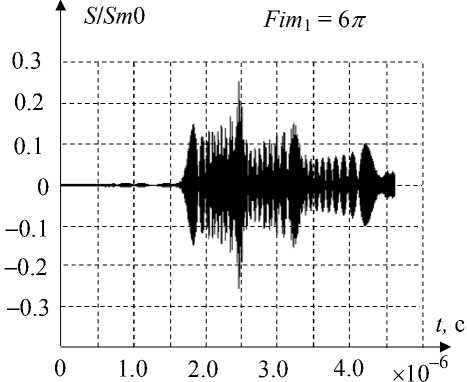
На рис. 6 показано изменение формы сжатого сигнала при различных значениях набега фазы (возмущающего сигнала) Fim 1 = 6 π (а) и Fim 1 = = 24 π (б), вызванного гармонической деформацией ( d =1) по закону (4). При снижении уровня ( Fim ) дополнительного изменения фазы ∆ ϕ до 0.1 % форма сигнала изменяется, но его уровень все-таки не превосходит (1/3) уровня невозмущенного сигнала (рис. 7).

ЗАКЛЮЧЕНИЕ

Основная область применения чувствительных элементов на основе дисперсионных линий задержки — бесконтактные (дистанционные) пассивные датчики. Топологические решения чувствительного элемента деформации, в частности давления, на основе дисперсионных линий задержки имеют высокую чувствительность к измеряемому параметру. В конструкции чувствительного элемента могут быть использованы как области постоянной деформации, так и области

а

Рис. 6. Зависимость формы сжатого сигнала от набега фазы возмущающего сигнала

S / Sm 0

Fim 1 = 24 п

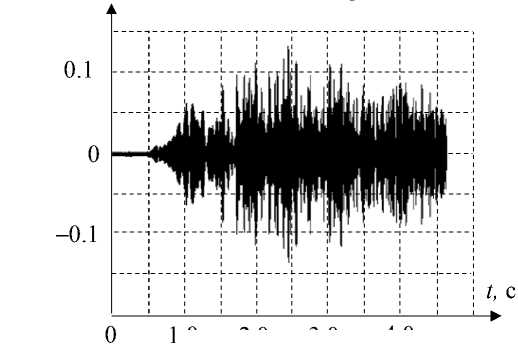
б

1.0    2.0    3.0

4.0       –6

x 10

S / Sm 0

Fim = 0.005; Fim 1 = 24 п

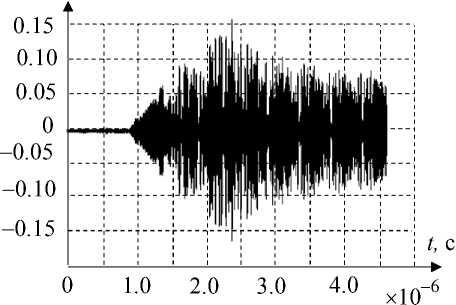
а

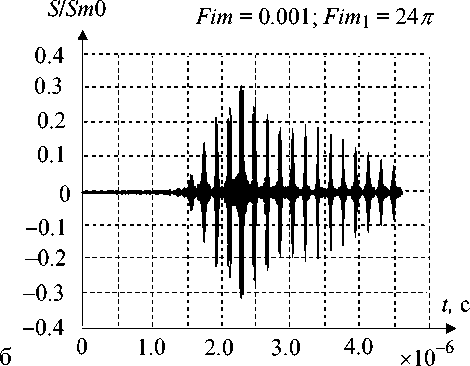
Рис. 7. Сжатый сигнал при 0.5 %-й (а) и 0.1 %-й (б) амплитудах фазы возмущающего сигнала

существенно изменяемой деформации. Применение частотной модуляции значительно увеличивает помехоустойчивость датчиков на поверхностных акустических волнах.