Цифровая модель геодинамических процессов в литосфере Земли

В научной литературе описаны существующие на настоящий момент времени глобальные модели земной коры – CRUST 5.1 и CRUST 2.0 [1; 2], представляющие собой распределенные по сетке данные соответственно с осреднением 5 °х 5 ° и 2 °х 2 ° , содержащие информацию о скоростях продольных и поперечных волн, о плотности во всех слоях земной коры, включая подкоровый, а также о глубинах раздела земной коры, включая границу Мохоровичича (Мохо). Принципиально отличается от них разработанная в 2013 году модель CRUST 1.0, представляющая собой уже 9-уровневую систему данных с осреднением по сетке 1 °х 1 ° [3].

Информация, представленная в этой модели, позволила выполнить количественные оценки таких важных распределенных параметров земной коры, как температура, вязкость, упругие модули напряжения, деформации, смещения для различных глубинных уровней земной коры [4; 5].

Полученная в результате проведенных исследований обширная числовая информация по характеристикам литосферных геодеформационных процессов дала нам возможность вплотную подойти к реализации задачи построения принципиально новой цифровой модели литосферы Земли, включающей в себя не только данные предыдущих моделей, но и рассчитанные авторами характеристики литосферных геоде-формационных процессов.

Развитие информационных систем в области геофизических исследований требует разработки новых подходов, стандартов и инструментария для представления знаний в области геодинамических процессов. Пока же создание целостного образа геодинамики Земли не находило реального воплощения в эффективной цифровой модели, включающей системные данные не только о геодинамических характеристиках, но и о связях между ними, описанные с помощью современных математических моделей. Создание цифровой модели видится в реализации таких современных концепций, как Industry 4.0 [6], рекурсивная декомпозиция данных [7], «цифровой двойник» [8].

Поскольку новую цифровую модель литосферы, представляющую собой современную базу данных (БД), необходимо наполнить самой разнообразной информацией о характеристиках литосферных геодеформационных процессов для различных глубинных слоев литосферы, с одной стороны, а с другой стороны, привязать эту информацию к конкретным географическим координатам, нами на настоящем этапе для построения БД была применена технология оперативной аналитической обработки данных OLAP (OnLine Analytical Processing).

Как известно, основой OLAP-технологии является построение многомерного представления данных, когда они даются не в форме реляционных таблиц, а в виде упорядоченных многомерных массивов двух видов [9]:

• 1)    гиперкубов (все хранимые в БД ячейки должны иметь одинаковую мерность, т. е. находиться в максимально полном базисе измерений);

• 2)    поликубов (каждая переменная хранится с собственным набором измерений, и все связанные с этим сложности обработки перекладываются на внутренние механизмы системы).

Гиперкубическая форма представления данных

В настоящей работе представлена гиперкубическая форма многомерных массивов данных. Предположим, что задана некоторая схема представления БД RD = = { R 1 ,R ₂, k , R k } , где R i - отношения, определенные на множестве атрибутов Л = = { L 1 ,L 2 , к , L n } (табл. 1). В фигурных скобках в таблице уточнены области определения некоторых атрибутов.

Для атрибутов установим следующие зависимости:

DEP = { L 2 L з L 16 ^ A, L 4 L 5Аб ^ A, L 6 L 7Ае ^ A, L 8 L 9Ае ^ A, AoAiАе ^ А, £ 12 £ 13 £ 16 ^ £ 1 , £ 14 £ 15 £ 16 ^ L } .                           ⁽¹⁾

Зависимости (1) соответствуют следующим отношениям:

• 1)    координаты ячейки R 1 { L 2 ,L 3 ,L 16 ,L 1 } ;

• 2)    экспериментальные характеристики литосферных геодеформационных процессов R 2 { L 4 , L 5 , L 16 , L 1 } ;

• 3)    расчетные характеристики литосферных геодеформационных процессов R 3 { L 6 , L 7 , L 16 , L i } ;

• 4)    нормальные геодинамические напряжения R 4 { L 8 ,L 9 ,L 16 ,L 1 } ;

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

• 5)    сдвиговые геодинамические напряжения R 5 { L 10 ,L 11 ,L 16 ,L 1 } ;

• 6)    смещения в геологической среде R ₆ { L ₁₂, L ₁₃, L ₁₆, L 1 } ;

• 7)    величина геодинамического риска R 7 { L 14 ,L 15 ,L ₁₆, L 1 } .

  Схема представления БД

  
  

Таблица 1

Обозначение атрибута	Содержание атрибута
L 1	Порядковый номер ячейки
L 2	Порядковый номер координаты
L 3	Наименование координаты {долгота, широта, глубина}
L 4	Порядковый номер экспериментальной характеристики литосферных геодеформационных процессов
L 5	Наименование экспериментальной характеристики литосферных геодеформационных процессов {плотность, скорость продольных волн, скорость поперечных волн}
L 6	Порядковый номер расчетной характеристики литосферных геодеформационных процессов
L 7	Наименование расчетной характеристики литосферных геодеформационных процессов {давление, объемный модуль упругости, модуль сдвига, температура, вязкость}
L 8	Порядковый номер компоненты нормальных напряжений
L 9	Наименование компоненты нормальных напряжений {σ x , σ y , σ z , σ r }
L 10	Порядковый номер компоненты сдвиговых напряжений
L 11	Наименование компоненты сдвиговых напряжений {τ xz , τ yz , τ xy , τ z }
L 12	Порядковый номер составляющей вектора смещений
L 13	Наименование составляющей вектора смещений { ux , uy , uz , ur }
L 14	Порядковый номер вида геодинамического риска
L 15	Наименование вида оценки геодинамического риска {вероятностная, энергетическая, нечеткая}
L 16	Количественное значение параметра атрибута

Гиперкуб определяется в виде совокупности измерений { D 1 ,D 2 , к ,D h } (где D s -множество имен атрибутов; s = 1, 2, …, h ) и множества имен атрибутов M , которые называются мерами. Значения D_s являются значениями координат гиперкуба, значения M располагаются в его рабочей области.

Для того чтобы в одной ячейке гиперкуба было не более одного значения атрибута меры, предполагается выполнение функциональной зависимости

D 1 , D 2 , K , D h → M .                             (2)

где D 1 = { R 1 .L 1 } , D 2 = { R 2 .L 5 } - измерения; M = { R 2 .L ₁₆ } - мера, или

{R1.L1 }x{R3 .L7 (R3 .L16 )},

где D 1 = { R 1 . L 1 } , D 2 = { R 3 . L 7 } - измерения; M = { R 3 .L 16 } - мера.

После того как сформирована схема гиперкуба с установлением иерархий в измерениях и присоединением мер к атрибутам измерений, воспользуемся простейшим методом решения задачи формирования гиперкуба по множеству отношений при отсутствии логических ограничений F (т. е. F = Ø), а именно: выполним операцию естественного соединения отношений для формирования промежуточного представления

БД:

TJ = R V ] Ф R2 [V ] Фк Ф Rk [V],                (5)

Затем значения координат формируются в виде проекций по соответствующим атрибутам: TJ[Ds ], с необходимой сортировкой кортежей каждого измерения в соответствии с иерархией. Завершается построение гиперкуба присваиванием значений мер M в его рабочей области, т. е. для каждого кортежа t∈ TJ на пересечении значе- ний координат t[Ds ] (где s = 1, h) ставится значение t[Lj ], Ri.Lj е M.

Описанная технология применена при построении БД характеристик литосферных геодеформационных процессов. Приведем фрагмент блока описаний переменных программы построения БД, реализованной на языке программирования Borland Delphi 7.0 (рис. 1).

type atom = record

• V alue1: real;

• V alue2: real;

• V alue3: real;

• V alue4: real;

• V alue5: real;

end;

molecula = record

Long: real;

Lat: real;

Depth: integer;

Around: array [1..8] of atom;

end;

var Pole: array [1..21] of byte;

Mode, Mode1: byte;

Litosphere: array [1..360, 1..180, 0..80] of molecula;

Plate: array [1..64800] of molecula;

A: molecula;

Z, Depth1, Depth2, X1, X2, Y1, Y2, XCount, YCount, ZCount: integer;

DepthFile: string[4];

Count, PointCoord, StartCoord, FinCoord: longint;

Longitude, Latitude, Long1, Long2, Lat1, Lat2: real;

Рис. 1. Фрагмент блока описания переменных программы построения БД

При описании переменных определены два типа данных: и . Оба типа определены как записи, но в первом случае запись структурно состоит из пяти вещественных полей, во втором случае – из двух, одно поле целочисленное, а другое само является записью типа .

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Графически элемент массива , являющийся объявленным типом данных , представлен на рис. 2.

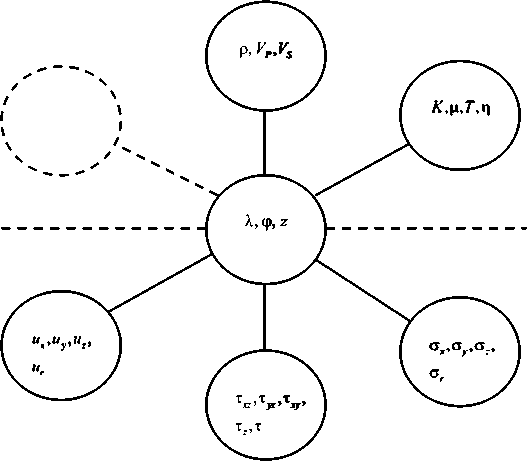
Рис. 2. Графическое представление элемента массива :

λ – географическая долгота; φ – географическая широта; z – глубина;

ρ – плотность вещества; V_p – скорость продольных волн; V_s – скорость поперечных волн; K – объемный модуль упругости; μ – модуль сдвига;

T – температура; η – вязкость; σ _x – x -компонента нормальных напряжений; σ _y – y -компонента нормальных напряжений; σ _z – z -компонента нормальных напряжений; σ _r – радиальные нормальные напряжения; τ _xz – сдвиговые напряжения в плоскости XZ ; τ _yz – сдвиговые напряжения в плоскости YZ ; τ _xy – сдвиговые напряжения в плоскости XY ; τ _z – вертикальные нормальные напряжения; τ – величина вектора полных напряжений; u_x – x -составляющая вектора смещений; u_y – y -составляющая вектора смещений; u_z – z -составляющая вектора смещений;

u_r – радиальная составляющая вектора смещений

Сам же массив представляет собой структурированную информацию о литосфере Земли, послойно размещенную в многомерной базе данных о характеристиках литосферных геодеформационных процессов.

Тип данных так назван потому, что он напоминает по своей структуре молекулу, состоящую из атомов. В такой «молекуле» имеется центральный «атом», содержащий информацию о координатах отдельной элементарной ячейки (элементарного объема литосферы), и ряд «второстепенных атомов», содержащих структурированную информацию о характеристиках литосферных геодеформационных процессов.

Возможности гиперкубического представления данных

Согласно структуре «молекулы» (см. рис. 2), в ней может быть определено до восьми «второстепенных атомов» (один такой «атом» показан пунктирной окружностью, к двум другим, пока не существующим «атомам», указаны связи в виде пунктирных линий). При построении БД участвуют только пять таких «второстепенных атомов». Это означает, что внутри БД предусмотрены дополнительные вычисления, позволяющие на основе имеющейся в БД информации выполнять расчеты и заполнять полученными данными «пустые» слои в БД.

Подобная структурная организация БД позволяет назвать ее символически «молекулярной базой данных».

Для работы с созданной базой данных о характеристиках литосферных геоде-формационных процессов (имеющей объем 1,67 Гб) разработана на языке программирования Borland Delphi 7.0 программа DMGRLE (Digital Model Geodynamic Risk Litosphere of the Earth – Цифровая модель оценки геодинамического риска в литосфере Земли), представляющая собой систему выборки и обработки информации из БД характеристик литосферных геодеформационных процессов.

В программе предусмотрены такие виды манипулирования данными, как «Срез» (Slice), «Отображение страницы» (Page Display), «Нарезка на кубики и ломтики» (Slice and Dice), «Вращение, пивотинг» (Rotate, Pivot).

«Срез» (Slice) – это созданное пользователем подмножество гиперкуба, получившееся в результате фиксации значения одного или более измерений.

Текущее представление среза многомерной информации называется «Отображением страницы» (Page Display). Измерения, расположенные по горизонтали (поперек дисплея), определяют измерения в столбцах таблицы.

Строки таблиц измерений определяются измерениями, расположенными по вертикали (вдоль дисплея). Выбор элемента измерения страницы позволяет определить, какая именно страница отображается в данный момент. Страница во многом напоминает обычную электронную таблицу и может быть интегрирована практически с любой программой электронных таблиц, где пользователь может в дальнейшем вносить изменения в каждую ячейку.

«Нарезка на кубики и ломтики» (Slice and Dice) – термин, использующийся для описания функции сложного анализа данных, обеспечиваемой средствами OLAP выборки данных (продольные и поперечные, плоскостные и объемные срезы) из многомерного куба с заданными значениями и заданным взаимным расположением измерений, при котором пользователь обычно использует операции вращения куба данных и детализации (либо агрегирования) данных. Такая возможность предоставляется пользователю при реализации как точечной, так и объемной выборки из массива данных БД характеристик литосферных геодеформационных процессов.

Изменение порядка представления измерений, применяемое при двухмерном представлении данных, называется «Вращением, пивотингом» (Rotate, Pivot). Эта операция обеспечивает возможность визуализации данных в форме, наиболее комфортной для их восприятия. Операция вращения может заключаться в перестановке местами строк и столбцов таблицы либо перемещении интересующих измерений в столбцы или строки создаваемого отчета, что позволяет придавать ему желаемый вид.

Выводы

• 1.    В статье представлена принципиально новая, не имеющая аналогов ни в отечественной, ни в зарубежной практике геофизических исследований, цифровая модель литосферы Земли, представляющая собой компьютерную базу данных характеристик литосферных геодеформационных процессов.

• 2.    При построении БД использована технология оперативной аналитической обработки данных OLAP с применением гиперкубического представления данных.

• 3.    Для работы с БД характеристик литосферных геодеформационных процессов разработана специализированная программа DMGRLE – Digital Model Geodynamic Risk Litosphere of the Earth (Цифровая модель оценки геодинамического риска в литосфере Земли), позволяющая не только формировать самые разнообразные запросы к БД, но и на более детальном и качественном уровне реализовывать различные модели оценки геодинамического риска.

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»