Цифровая обработка сигналов на графах

В современном обществе практически вся информация находится в цифровом пространстве. Цифровые данные окружают нас повсюду, и каждый аспект человеческой жизни может быть записан: внутриклеточные процессы, действия и запросы в интернете, финансовые транзакции, путешествия, приложения для отслеживания здоровья и др. Сложность таких сетей означает, что данные теперь хранятся на нестандартных и сложных конструкциях, не всегда поддающихся классическим статистическим методам обработки данных.

Представление сигналов в виде графа позволяет моделировать подобные данные со сложными взаимодействиями между ними. Например, пользователи приложений могут быть смоделированы как вершины, их запросы и обращения к тем или иным услугам, вкладкам, помощи, внутренним или внешним ресурсам – как ребра графа. Обработка сигналов на графах позволяет добавить определенные атрибуты к таким вершинам и моделировать их как сигналы на графах. При обработке цифровых сигналов их можно фильтровать, семплировать, то есть управлять начальной выборкой при известной цели, и это одна из наиболее сложных задач; их можно очищать от шума, изучать их структуру, моделировать процессы, происходящие внутри данных или при выходе из структуры графа. Обработка сигналов на графах плотно связана со многими теоретическими и практическими областями исследований; с ее помощью можно разработать новые инструменты и подходы к решению существующих проблем. Основой цифровой обработки сигналов стали работы Оппенгейма [6] и других авторов.

Цифровая обработка сигналов на графах

Попова Татьяна Михайловна кандидат физико-математических наук, доцент, доцент кафедры прикладной математики, Тихоокеанский государственный университет, город Хабаровск. Сфера научных интересов: математическое моделирование физических, гидрологических процессов, обработка и анализ данных. Автор более 60 опубликованных научных работ.

Сигналом на графе назовем множество значений, принадлежащее множеству вершин, которые связаны взвешенными ребрами. Сами сигналы могут брать свое начало в различных областях, но в отличие от классической обработки сигналов, лежащий в основе граф несет в себе определенную информацию о них. Разные типы графов позволяют моделировать разные типы связей, которые эти узлы представляют. В основном цифровая обработка сигналов изучает: сигналы и их представление; системы, обрабатывающие сигналы (фильтры); преобразование сигналов; семплирование сигналов. Фильтр – это система, избирательно меняющая форму сигнала (амплитудно-частотную или фазово-частотную характеристики). Цифровой фильтр – это определенная аппаратная или программная реализацию алгоритма фильтрации. В цифровых фильтрах используются оцифрованные отсчеты аналоговых сигналов или хранящиеся в памяти числа.

Обработка дискретных сигналов данных со сложной структурой

Опираясь на концепцию теории алгебраических и спектральных графов, ряд авторов предложили новую структуру обработки дискретных сигналов для представления и анализа наборов данных со сложной структурой [7–9]. Они расширили традиционную теорию дискретной обработки сигналов до структурированных наборов данных, рассматривая их как сигналы, представленные графами так, что выборки сигналов указываются вершинами графа, а отношения между ними представлены взвешенными ребрами. Были определены понятия сигналов и фильтров на графах, а также понятия спектра и преобразования Фурье для сигналов на графах. Вопросы расширения идей и концептов стандартной обработки сигналов на графы могут быть разделены на категории стационарности и локализации.

Стационарность обычного сигнала во времени проверяется либо влиянием сдвига на статистические характеристики сигнала, либо путем наблюдения за самим сигналом в разные промежутки времени. Также можно определять стационарность, основываясь на спектральных свойствах оператора сдвига на вершинах [4]. Для решения проблем с существующими операторами сдвига было предложено использовать другой оператор [3]. Важная проблема семплирования – выборка значимых значений, по которой можно восстановить всю структуру с минимальными погрешностями – следует из той же проблемы классической обработки сигналов. Но на графах не проходит обычная модель семплиро-вания, необходимо определить методы отбора наиболее информативных вершин.

N - 1

s(z ) = ^snz — n ■                                       (1)

n = 0

Фильтром назовем систему, преобразующую исходный сигнал, который можно записать аналогично (1):

N - 1

h(z ) = Zhnz—n ■

n = 0

Так, выходной сигнал s _eux фильтра h , примененного к входящему s _exod , s eux ( ^z ) = h ( z ) s exod ( z )

с фильтром h _cdeu2 ( z ) = z ¹ , который называется сдвигом. Фильтр h представим как матрицу H . Это позволит переписать (3) в матричном виде:

^S eux = H "  ^S exod ^{.                                           (4)}

Сдвиг – это основной элемент цифровой обработки сигналов, позволяющий составлять более сложные фильтры. Различные типы применения некоторых фильтров рассмотрены в работах [1; 2].

Рассмотрим граф G = ( V , E ) , где V = { 0,1, . , N - 1 } - множество вершин, определяющие выборки сигналов s = [ s ₀ s 1 . s_N - 1 ]^Г e C ^N , а E - множество ребер между смежными вершинами (то есть соединенными ребром) с матрицей смежности, определяющей матрицей сдвига

" 0 0 0 — 0 1 " 1 0 0  —  0 0 0 10 — 0 0 .                  • A c = : : \  \ \ 0 0 0 —  1  0 0 0 0 — 0 10 а операцию сдвига – произведением

" N - 1 ^s 0 . ^s N - 2 ]

A c •[ ^s 0 ^s 1 . ^s N - 1 J .

Применение фильтра является умножением каждой выборки сигнала на коэффициент h_n = { h n : n = 0, . , N - 1 } . В системе на графе это можно представить выражением

N - 1

Seux  ^ hnL Sexod, n=0

где L = D - A - лапласиан графа; D - диагональная матрица степеней вершин графа (количество связей с остальными вершинами графа); L ⁿ – спектральное представление Лапласиана,

Цифровая обработка сигналов на графах

N - 1

Ln = U Л U-1 =^Anunu;1,

n = 0

где    U = [ u 0 u1... u_{N - 1} ]    - ортонормированная матрица собственных векторов;

Л = diag [ 2 0 2 1 . 2 _N 1 ] - диагональная матрица собственных значений лапласиана.

Подставляя в соотношение (5), получим

N - 1

seux =^hn UЛ n U-1 sexoa = U h (Л)U-1 sexod, n=0 где

N - 1 h ( л ) = ^ Л n , n = 0

h ( Л ) - передаточная функция системы на графе.

В работе [12] даны теоретические объяснения, когда и почему спектральное представление оператора Лапласа можно рассматривать как значимое преобразование Фурье для достаточно гладких сигналов.

Использование фильтров в спектральной области достаточно прямолинейно и выполняется в три этапа:

• 1.    Вычисление преобразования Фурье на графе входящего сигнала Fs = U ¹ s .

• 2.    Умножение результата на передаточную функцию Fs = h ( Л ) F s .

• 3.    Получение выходного сигнала путем вычисления обратного преобразования Фурье s = UFs.

Проектирование фильтров это один из основных этапов моделирования сигналов на графах. Могут быть использованы уже известные фильтры, адаптированные или специально созданные для графов [5].

Рассмотрим применение различных фильтров на сенсорном и кластерном графах. На Рисунках 1, 2 смоделированы начальный и искаженный сигналы. Использованы следующие фильтры: теплового ядра, алгоритм Таубина и произведение (свертка) этих фильтров. Применение таких фильтров для спирального графа рассматривалось в работе [1].

Представим граф, в котором каждая вершина имеет температуру, а тепло может переходить только по ребрам между вершинами. Распространение тепла на таком графе будет следовать закону Ньютона – Рихмана и должно быть пропорционально весу ребра и разнице температур между вершинами. Пусть snt) - температура вершины n во время t, тогда теплопередачу на графе можно выразить уравнением j (t)        N-1

ds^ = - k £ a nm ( s n ) - s < t ) ) = n = 0

—J

⁽ t ⁾_Х"¹д k D nn s n   / A;

5 ( t ) nm m

которое в матричной форме уравнение примет вид

n = 0

ds^ = - k L s ⁽ t ) . dt

При замене параметров t и k в один tf = kt, это уравнение можно переписать как ds(t')

—

dt '

L s ⁽ t ') .

Тепловое ядро H _t – это фундаментальное решение уравнения теплообмена. Оно определяется квадратной матрицей H t = e - L t . Тепловое ядро можно рассматривать как многочлен лапласиана, значит, его можно использовать как фильтр низких частот [10; 11].

Рисунок 1. Сигнал s и шум y на сенсорном графе: а – изначальный сигнал на графе; б – искаженный сигнал

Рисунок 2. Сигнал s и шум y на кластерном графе: а – изначальный сигнал на графе;

б – искаженный сигнал

Алгоритм Таубина представляет собой итерационный алгоритм вида

• ^s p + 1 = s p ^{- а} L ^s p = ( E ^{- а} L ) s p ,

который можно использовать в качестве простого, но эффективного фильтра сигналов на графах [14]. Так как минимумом квадратичной формы является константа, чтобы избежать получения только постоянного сигнала в результате стоит использовать его пооче редно с sp+2 =(E + eL)s p+1"

Компактная форма этого алгоритма называется алгоритмом Таубина:

Цифровая обработка сигналов на графах sp+2 =( E - aL)(E + pL) Sp.

Передаточная функция данного фильтра имеет вид

h( A ) = (1 + (6 n - 6 n ) An - 6 n6 n^n )P , где p – количество итераций.

Применение описанных фильтров на графах разной структуры

Рассмотрим применение описанных фильтров на графах разной структуры: стандартном сенсорном графе и кластерном. Количество вершин – 120. Введем определенный сигнал s и шум y , искажающий данный сигнал. Значения выборок на всех графах будут одинаковы, как и их искажение, различия на данном этапе будут только в связях, так как шум изменил значения некоторых выборок сигнала, и теперь некоторые вершины графов имеют другие цвета (см. Рисунок 1).

Рассмотрим каждый сигнал на графе в отдельности, применив каждый фильтр, чтобы очистить их от шумов, и проанализируем их эффект. Выберем значения коэффициентов таким образом: α = 0,4, β = 0,2, t = 0,2; количество итераций p = 25. Получим следующий результат (см. Рисунки 3, 4). Для критерия эффективности применения того или иного фильтра была использована метрика расхождения между исходным и очищенным сигналом типа евклидова расстояния между соответствующими вершинами (разности в цвете).

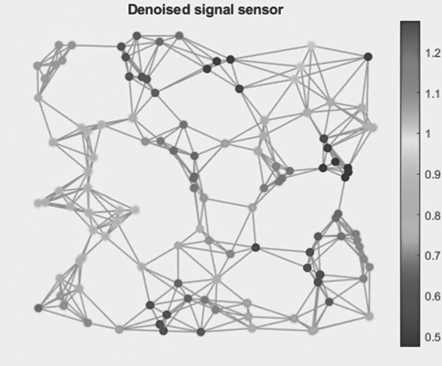
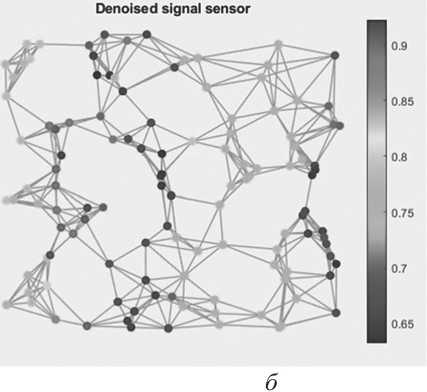
Рисунок 3. Результат применения фильтра теплового ядра ( а ), фильтра с алгоритмом Таубина ( б )

Фильтр теплового ядра очистил сигнал недостаточно хорошо – большинство выборок приблизилось к своим изначальным значениям совсем немного, а некоторые даже отдалились. Можно заметить, что в целом сигнал стал более однородным – преобладают низкие частоты. Алгоритм Таубина дал заметно более хороший результат по сравнению с тепловым ядром. Из явных ошибок данного фильтра можно выделить только увеличение частоты некоторых выборок, предположительно, из-за большого значения β. Евклидово расстояние D ( s _вход, s _вых) = 0,089.

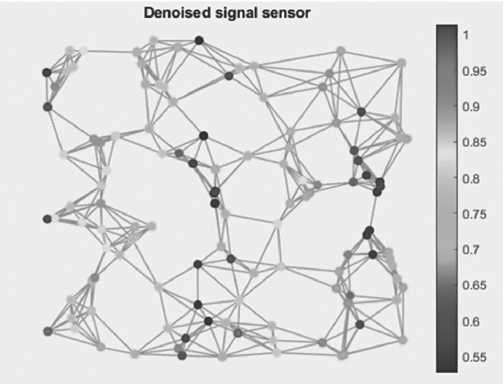
Рисунок 4. Результат применения свертки фильтров

Произведение фильтров дало схожий результат с тепловым ядром. В местах, где преобладали высокие частоты, фильтр сильно увеличил значения выборок, но в основном значения стали меньше. При данных параметрах использование произведения фильтров не оправдано. Евклидово расстояние D ( s _вход, s _вых) = 0,141.

Далее рассмотрим результаты работ фильтров на кластерном графе (см. Рисунки 5, 6).

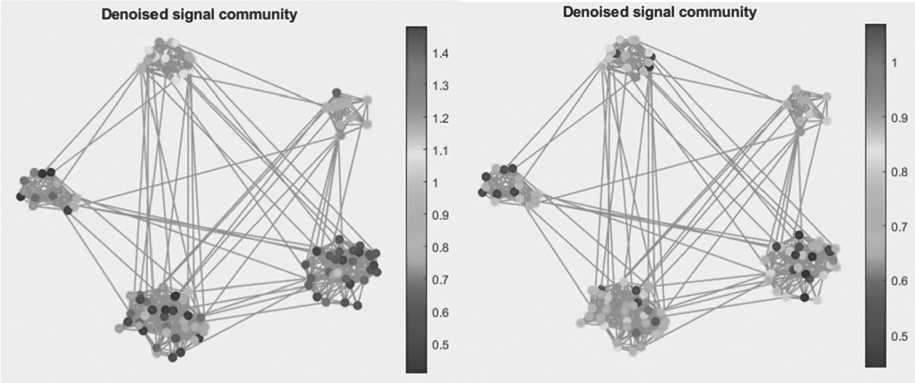
Рисунок 5. Результат применения фильтра теплового ядра ( а ), фильтра с алгоритмом Таубина ( б )

Фильтр Таубина на кластерном графе показал очень хороший результат, так как значения большинства выборок сильно приблизились к изначальным. Евклидово расстояние D ( s _вход, s _вых) = 0,037, но произведение фильтров работает неудовлетворительно – практически все значения выборок исказились еще больше по сравнению с результатом шума. Но стоит обратить внимание на то, каким образом фильтр распределил значения: в рамках каждого кластера все значения схожи между собой, что позволяет выделить свойство сортировки данного фильтра на данном графе, и это может привести к различным применениям данного фильтра, несмотря на то, что шум не был очищен.

Цифровая обработка сигналов на графах

Рисунок 6. Результат применения произведения фильтров

В работе [1] показано, что на спиральном графе тепловое ядро показывает относительно низкую эффективность, а фильтр алгоритма Таубина справился достаточно хорошо, несмотря на то, что в некоторых местах с высокими частотами он сильно снизил значения выборок. Произведение фильтров выявило наименьшую из всех метрику расхождений, следовательно, дало наилучший результат из всех рассматриваемых моделей.

Заключение

Таким образом, можно сделать вывод, что применение того или иного фильтра зависит от вида графа, описывающего процесс и дает широкие возможности по компоновке разных типов фильтров. В итоге наилучшим фильтром при отсечении шумов оказался фильтр, основанный на алгоритме Таубина: он показал отличный или хороший результат для всех рассматриваемых типов графов. Фильтр теплового ядра в данных экспериментах, напротив, дал наихудший результат, поэтому стоит провести более подробные исследования по нахождению подходящего применения этого типа фильтра.

Новый тип фильтра, представленный в данной работе и работе [1], показал смешанные результаты. Так, на сенсорном графе результат был подобен результату теплового ядра, на спиральном новый фильтр дал наилучший результат из всех рассматриваемых, а на кластерном, несмотря на наихудший результат очистки, было выявлено свойство сортировки, которое может быть полезно в определенных приложениях.