Цифровое и широтно-импульсное управление космическим роботом при сближении с геостационарным спутником

Информационные спутники (связи, метеорологического наблюдения Земли) на геостационарной орбите (ГСО) имеют потребную длительность службы до 25 лет при наличии технического обслуживания с помощью космических роботов-манипуляторов (КРМ), в частности дозаправки топливом их электроре-активных двигательных установок (ЭРДУ). Ограничения на допустимую массу затрат топлива при выведении крупногабаритного космического аппарата (КА) на ГСО приводят к проблеме «до-выведения» КА от переходной орбиты до геостационарной с помощью бортовой ЭРДУ[1]. В статье [2] представлены суть проблемы и бюджеты вывода КРМ массой m ® 3000 кг на ГСО при его запуске с указанным «до-выведением». В системе управления движением (СУД) КРМ

применяются следующие приводы: ЭРДУ с тягой P = 0.58 Н, двигательная установка малой тяги (ДУМТ) на основе 8 реактивных двигателей (РД) с широтно-импульсной модуляцией (ШИМ) тяги P^m = 0.5 Н каждого РД (рис. 1) и силовой гироскопический кластер (СГК) по схеме 2 Scissored Pair Ensemble ( 2-SPE ) на основе четырёх гиродинов (ГД) с собственным кинетическим моментом (КМ) h _g = 30 Нмс, рис. 2.

Данная статья посвящена проблемам наведения и управления пространственным движением КРМ при его сближении с геостационарным спутником (целью) с расстояния 5 км до дальности 50 м для последующей визуальной инспекции его технического состояния.

МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Для описания движения КА применяются геоцентрическая I _е ( O _e X i Y i Z i ) и солнечно-эклиптическая I _s инерциальные системы координат (ИСК), обозначения { • } = col0, [ • ] = lineQ, 0*,[*] и ° ,~ для векторов, матриц и кватернионов, i = 1,2,.. m = 1 ^ m. Используются орбитальные системы координат (ОСК) O_r x ^o y ^o z ^o КРМ с полюсом O_r и цели O_t x _t ^o y _t ^o z _t ^o с полюсом O_t . Вектор тяги РДУ направлен по оси O _ry связанной с корпусом КРМ системы координат (ССК) O_r xyz , а для инспекции цели на борту КРМ применяется телескоп с осью визирования параллельной этой же оси. Если КРМ считать твёрдым телом массой m , то модель

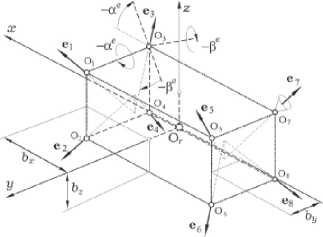
Рис. 1. Схема ДУМТ на основе восьми РД

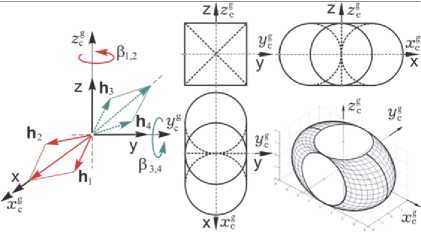
Рис. 2. Схема 2-SPE СГК на основе четырех ГД

его движения в ИСК I _е в проекции на оси ССК O r xyz имеет вид

г * + m x r = v ; m ( v * ■ m x v ) = P ^e + F ^d;

Л = Л о ю/2; J m + m x G = Mg + Me + Td, где кватернион Λ представляет ориентацию КРМ в ИСК, вектор G =J ω + H , где H – вектор КМ СГК, используются векторы тяги Pe и момента Me двигательной установки, момента Mg = —H* СГК, векторы внешних возмущений Fd, Td и символ (•) локальной производной.

При законе углового наведения робота, заданного кватернионом Л p ( t ) , погрешность ориентации его ССК O_r xyz определяется кватернионом Е = ( e ₀, е ) = Л p ° Л при e = {e i } , которому соответствуют матрица ошибки ориентации C ^e = I ₃ — 2[ e x ] Q e , где Q _e = I ₃ e ₀ + [ e x ] , вектор модифицированных параметров Родри-га a ^e = { a ■ } = e / (l + e ₀) = e ^etg( Ф ^e/4) с ортом e ^e оси Эйлера и углом Ф ^e собственного поворота, а также вектор угловой погрешности 5ф = {5ф _/ } = {4 о e } .

На рис. 1 орты e _p , p = 1 ^ 8 по осям сопел РД и параметры b b задают вектор р _p точки O _p приложения вектора тяги p -го РД. ШИМ тяги p ( t ) представляется моделью P p (t ) = Р ' PWM( t — T ^ , t s , T m ,V pr ) V t G [ t s , t s + 1 )

при периоде T U и запаздывании T ^u . Здесь P ^m представляет тягу, одинаковую для всех РД, t_s = sT®, s G N₀ = [0,1,2,...) и функции

PWM( t,t s , T m ,V ps ) =

' sign ^v ps    t ^{G [} t s ,t s ^{+ T} ps ⁾ ,

0     ... t ^{G [} t s ^{+ T} ps ^, t s + i );

T (t ) = ps m

^

sat ^{( T}:^, | ^v ps |)

^|V ps ^| - ^T m ^{; |v} ps ^| > ^T m .

Вектор тяги РД p _p ⁽ t ) = ^— p_p ⁽ t ) e _p , векторы тяги P ^e и момента M ^e ДУМТ формируются как P ^e = s p p ( t ) и M ^e = s [ p p X ] p p ( t ).

Столбец Н ( в ) = h _g h = S h _p ( P _p ) представляет вектор КМ СГК, где | h _p | = 1 , p = 1 ^ 4 . При цифровом управлении скоростями ГД

U К. t ) = {u ^gk ( t )}, u ^gk ( t ) = u ^gk V t G [ t_k , t k + 1 ) в моменты t k = kT_u с периодом T_u , k g N₀, вектор M ^g = { M i ⁸} управляющего момента СГК представляется соотношениями M k ( t ) = — h g A h ( P ( t ) u k ( t ) ; в ( t ) = u k ( t ) , где столбец в = {P } и матрица Якоби A h ( р ) = d h ( p ) /dp . ^Р

Предполагается, что СУД КРМ имеет бесплат-форменную инерциальную навигационную систему (БИНС) с инерциальным измерительным модулем гироскопов и акселерометров, которая корректируется сигналами спутников ГЛОНАСС/ GPS, а при дальности менее 500 м координаты траекторного и углового движения КРМ относительно цели определяются также оптико-электронными камерами наблюдения и лидарами [3].

Задача состоит в синтезе законов наведения и управления пространственным движением КРМ при изменении его дальности до цели с 5000 м до 50 м, а также в нелинейном анализе динамики СУД КРМ при таком сближении на основе компьютерной имитации.

АЛГОРИТМЫ НАВЕДЕНИЯ И УПРАВЛЕНИЯ

В начальный момент времени t i в ИСК известны векторы расположения и скорости поступательного движения КРМ г _г ( t i ) , v _r ( t i ) и цели r _t ( t i ) , v _t ( t _i). При введении опорной круговой орбиты радиуса r r ( t i ) = const в плоскости земного экватора удобно использовать цилиндрическую систему координат (ЦСК) [4]. Здесь координатами являются значения радиали r и угла u её отклонения от произвольного направления в плоскости опорной орбиты, а также смещения z в направлении, ортогональном этой плоскости.

Пусть w^r , w t и w z представляют радиальную, трансверсальную и боковую компоненты вектора управляющего ускорения КРМ, а µ – гравитационный параметр Земли. Движение КРМ при его сближении с целью (рис. 3) в центральном гравитационном поле на интервале времени t g [ t i , t f ] описывается уравнениями

2 2 r r — ru +ц / r = w ;

t 3 z ru + 2 ru = w ; z + ц z / r = w при известных краевых условиях по орбитальным переменным ЦСК. Здесь на основе аналитических соотношений [4] выполняются прогноз положения rp (t) и скорости vf (t) цели на интервале времени t е [ti, tf ] и аналитический расчет векторов rt (tf), vt (tf). Синтез закона наведения КРМ в его поступательном движении выполняется на основе параметризации его сближения в виде векторных сплайнов времени t е [ti, tf] с тремя участками постоянного управляющего ускорения для радиали r(t), угла u(t) и отклонения z(t), где ускорение отсутствует на среднем участке. Такой закон наведения определяет векторы rf (t), vf (t) и wf (t), где аналитически вычисляются моменты времени переключения ускорения wr (t), и позволяет далее вычислять разности между расположениями цели и КРМ Дг(t) = rt (t) — rr (t), их скоростями Av(t) = vt (t) - vr (t) и разности p  pp  p  pp

Дг (t) = r (t) — rr (t), ДV (t) = Vt (t) — Vr (t).

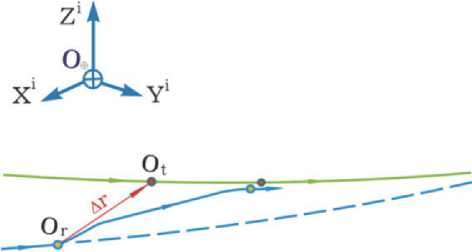
Рис. 3. Схема сближения КРМ с целью

Закон углового наведения КРМ в ИСК определяется программными значениями кватерниона Л ^f ( t ) , векторов угловой скорости to ^p ( t ) = { to f ( t )} и углового ускорения 8 ^f ( t ) = { 8 f ( t )} .

В дискретном алгоритме управления ДУМТ используется вектор δ ∆ r _s = ∆ r _s ^p - ∆ r _s рассогласования между программной разностью A r S = A r ^f ( t_s ) и измеренной разностью A r s = A r ( t_s ) расположений цели и робота, причём значения вектора δ∆ r _s формируются в ССК робота с периодом Т Ц в моменты времени t_s , s е N₀. В этом упрощенном алгоритме сначала вычисляется командный вектор I S импульса тяги ДУМТ на интервале времени t е [ t_s , t_s + 1 ) по формулам

g : + 1 = k b g : — k b Ь Д г s ;

P s = k : ( g : — k p ^);         (2)

Is = TU m (Os wp + ps), а затем для его реализации с помощью ШИМ тяги всех 8 РД вычисляются длительности τps ≤τm их включения по явным соотношениям.

В алгоритме цифрового управления ориентацией КРМ с периодом Tu определяются векторы углового рассогласования εk = -δφk и угловой скорости ωk для вычисления потребного управляющего момента СГК M® в виде а1  = к^ р^ + к^ p gfpg + к6

• ^g k +1 k b ^g k ^{+ k}c ^e k ; ¹¹¹k k u ^(g k ^{+ k}p ^e k ⁾ ;       (3)

м *=ю,х Gk+j(o: ep+[о: ю p х]ю,+inj, k       k       k           k К        k К      k       k где вектор Gk = Jtok + Hk, а затем вектор Mg распределяется между ГД по явным соотношениям и формируется вектор цифрового управ-

■ ления uk(t) = e (t) СГК Vt е [tk, tk+j) .

НЕЛИНЕЙНЫЙ АНАЛИЗ ДИНАМИКИ СИСТЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ

Компьютерный анализ выполнялся для модели (1) при указанных законах наведения и управления (2), (3). В стратегии сближения КРМ с целью от 5 км до дальности 50 м предусмотрено два этапа :

• 1)    подход КРМ с применением ЭРДУ и СГК на расстояние 500 м вслед за целью вдоль её орбиты, близкой к геостационарной;

• 2)    сближение КРМ с целью до дальности 50 м с помощью ДУМТ и СГК, подготовка КРМ к инспекции цели с номинальной точкой стояния Ω g = 76 град ВД на ГСО с номинальным радиусом r_g = 42164172.93 м.

При стандартных обозначениях перигея r_p , апогея r_a , наклонения i и долготы восходящего узла Ω орбиты были приняты начальные параметры орбит цели r_f = r g , r a = r g + 1000 м, i = 0 , ^ = ^ _g +24.46 угл. сек и робота r_f = r g - 500 м, r a = r_g + 2000 м, i = -20 угл. сек, Q = Q _g при нулевых значениях аргументов перигея и моментов времени их прохождения. При имитации сближения робота с массой m = 3000 кг и тензором инерции J = diag(3248,2348,3640) кгм² применялись период ШИМ тяги РД в составе ДУМТ Т Ц; = 4 с при запаздывании T Z:_u = 0.25 с, период цифрового управления ГД в составе СГК Т_и = 0.25 с и отсчет времени от значения t = 1 0 = 0 .

В начале этапа 1 на полуинтервале времени t ∈ [0, 70) с выполняются обработка измерений БИНС, прогноз движения цели и синтез закона наведения робота для достижения дальности 500 м до цели. Далее следуют:

• (i)    первый пространственный поворотный маневр (ПМ-1) КРМ V t е [70,170) на угол 26 град и угловая стабилизация V t е [170,270) с;

• (ii)    разгонный импульс тяги ЭРДУ V t е [270,4498) с, ПМ-2 V t е [5660,5860) с на угол 156 град, тормозной импульс тяги ЭРДУ V t е [5960,10168) с и, наконец,

  
  
  

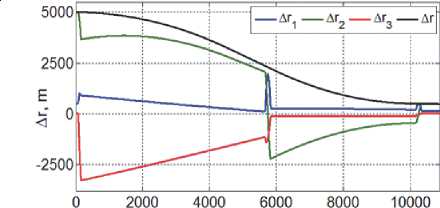
  t,S

  
  
  

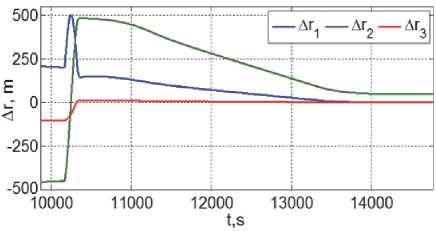
  Рис. 7. Расположение цели в ССК КРМ

  
  

  Рис. 4. Расположение цели в ССК КРМ

  
  
  

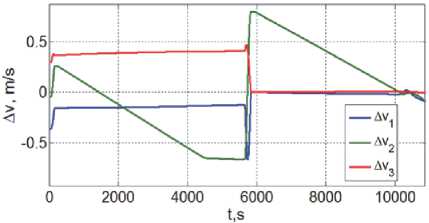
  Рис. 5. Разность скоростей цели и КРМ в ССК

  
  
  

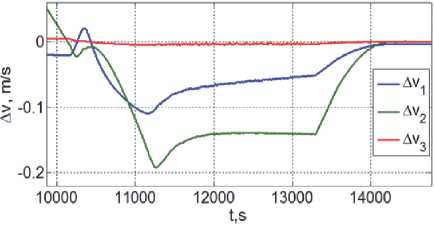
  Рис. 8. Разность скоростей цели и КРМ в ССК

  
  
  

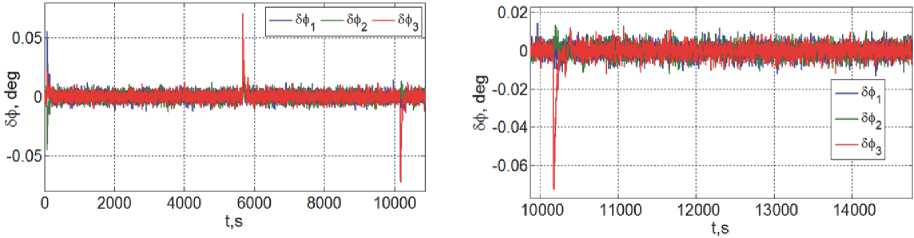
  Рис. 9. Погрешности угловой стабилизации КРМ

  
  

  Рис. 6. Погрешности угловой стабилизации КРМ

  
  

• (iii)    поворотный маневр ПМ-3 V t е [10168,10368) с на угол 138,7 град.

Этап 2 сближения КРМ с целью от расстояния 500 м до дальности 50 м имитировался на интервале времени t е [10368,14468] с, когда координаты пространственного движения КРМ относительно геостационарного спутника определяются бортовыми электронными приборами.

Полученные результаты приведены на рис. 4 – 9 с малым перекрытием по времени, где цветом выделены изменения переменных по рысканию (синий, ось x ), крену (зеленый, ось y ) и тангажу (красный цвет, ось z ), а модуль расстояния на рис. 4 представлен черным цветом.

ЗАКЛЮЧЕНИЕ

Кратко представлены методы наведения, цифрового и широтно-импульсного управления пространственным движением робота при его сближении с геостационарным спутником, а также численные результаты, демонстрирующие эффективность разработанных алгоритмов.