Цифровое и широтно-импульсное управление ориентацией спутника землеобзора

В системах управления ориентацией (СУО) малых информационных спутников традиционно применяются электромеханические приводы в виде кластера реактивных двигателей-маховиков (ДМ) с разгрузкой накопленного кинетического момента (КМ) магнитным приводом (МП). Известная минимально-избыточная схема General Electric ( GE ) обладает возможностью управлять ориентацией космического аппарата (КА) при отказе любого одного маховика. При требовании малых финансовых затрат в таких СУО применяются инерциальная система определения углового положения (СОУП) с солнечно-магнитной системой (СМС) коррекции, цифровое управление ДМ и широтно-импульсное управление магнитным приводом [1] - [5].

В статье рассматриваются задачи калибровки и юстировки СОУП с СМС коррекции, дискретной фильтрации измерений, полетной идентификации и компенсации моментов сил сухого трения по осям вращения ДМ, синтеза алгоритмов цифрового и широтно-импульсного управления, а также задача анализа динамики СУО спутника землеобзора.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ

В системе координат O xyz , связанной с корпусом КА (ССК), оси вращения четырёх ДМ по схеме GE располагаются на конусе с углом полу-раствора у [1]. Далее используются стандартные обозначения col0 = { • } , lineQ = [ • ] , ( • ) t , [ a x ] и о ,~ для векторов, матриц и кватернионов. Вводятся орбитальная система координат (ОСК), кватернион Л ⁰ и углы ориентации

Сомов Евгений Иванович, ведущий научный сотрудник отдела «Динамика и управление движением».

ССК относительно ОСК по крену ф1, рысканию ф2 и тангажу ф3, которые используются при формировании матриц элементарных поворотов [фi ]i в последовательности 312 при индексах осей i = 1,2,3 = 1 ^ 3 = x, y, z. Кватернион ориентации КА в инерциальной системе координат (ИСК) представляется как Л = Л 0 о Л0, где Л 0 - кватернион ориентации ОСК в ИСК. Модель углового движения КА учитывает упругость его конструкции и имеет вид

Л = Л о _ю/2 ; A ⁰{< b , q , Q } = { F “ , F ^q, F ⁿ } ,(1) F “ =- [ ю x ] G + M ^m + M ^d ;

F q =- A q ( V q q + W q q ) ;				F n = M - M f
	J	D q	A "
A 0 =	D t q	Α q	0	;
	_ J r A ‘	0	J r 1 4 .

	" C у	C У	C У	C у
A =	S у	- S у	0	0
	_ 0	0	S у	- S у

Здесь G = J o + H , столбцы H = { H i } и h = ^{{ h} p = J r ^ p ^} , p = ¹ ^ ⁴ , представляют КМ кластера и КМ отдельных ДМ, которые связаны соотношением H = A h , где матрица A составлена из ортов осей вращения ДМ в ССК;

A q = diag{ ц ₇ }; V q = diag{|Q j };

W q = diag{( Q j )²}; M ^m = { m™};

^M = ^{ m p ^} ; M ^f = ^{ m p ^} ;

C у = cos у , S y = sin у ;

вектор механического момента МП Mm = {m™} = -L x B, где вектор электромаг- нитного момента L = {li} с ограниченными компонентами | li |< lm и вектор индукции магнитного поля Земли B = b B с ортом b определены в ССК; векторы-столбцы M = {mp } и Mf = {mp } представляют управляющие моменты и моменты сил сухого трения по осям вращения ДМ, а вектор Md - возмущающие моменты. Ресурсы каждого ДМ по управляющему и кинетическому моментам ограничены, что представляется соотношениями | mp(t) |< mm,| hp(t) |< hm.

Проблемы обработки сигналов в инерциальной СОУП связаны с интегрированием кинематических уравнений по информации только о векторе дискретных приращений квазикоординат, получаемого инерциальным измерительным модулем (ИИМ) при наличии шумов измерений, с калибровкой и юстировкой – идентификацией и компенсацией погрешности взаимной угловой установки систем координат ИИМ и СМС на основе ее сигналов с периодом T_o . Угловое движение маневрирующего спутника земле-обзора осуществляется на последовательности временных интервалов выполнения маршрутов и поворотных маневров (ПМ) с переменным направлением вектора ω , модуль которого может достигать 1 град/сек.

В алгоритмах СОУП привлекается информация о значениях вектора приращений квазикоординат в промежуточных точках с периодом T , кратным периоду дискретности ^q

To , используются методы полиномиальной аппроксимации и выполняется численное интегрирование кинематического уравнения для вектора модифицированных параметров Родрига ст = e tg(0/4) (далее просто вектора Родрига), который связан с кватернионом Λ прямыми ст = Х/(1 + X 0) (Л^ст) и обратными X = 2ст /(1 + ст2) ; X 0 = (1 -ст2)/(1 + ст2) (ст > Л) соотношениями. Кинематические уравнения для вектора σ имеют вид

ст = F ст = ^4(1 + ст2>to +1стхto +1 ст<ст, to> ;

to = F “ = 4[(1 - ст ² ) ст - 2 ( ст х ст ) +

2ст < ст,ст >]/(1 + ст2)2.

Вводятся виртуальный базис A , вычисляемый на основе обработки информации от СМС коррекции, и виртуальный базис ИИМ G , вычисляемый на основе информации от интегрирующих гироскопов. Пусть измерительная информация обрабатывается в ИИМ и в результате от него в моменты времени t_s с периодом T q <  T o , t s _{+ 1} = t s + T q , поступают значения вектора приращений квазикоординат i m° S , s е N₀ , а от СМС - значения кватерниона Л m k = Л m ( t k ) , t k +1 = t k ⁺ T o , k е No с периодом T o :

i' = [s' " to m(r>dT Int (ts, Tq, to m (t)) + 5J ; ts togm( t) ^ (1 + m) S A (to (t) + bg);                (2)

л m k = л k о л k .

Здесь to m ( t ) представляет измеряемый вектор угловой скорости КА в базисе G с учетом неизвестных вариаций вектора b ^g = b ^g( t ) дрейфа ИИМ по угловой скорости, ортогональная матрица S ^Л ( t ) описывает погрешности взаимной угловой установки систем координат ИИМ и СМС, скалярная функция m = m ( t ) представляет неизвестную масштабного коэффициента ИБ, учтены гауссовские шумы 5 n с СКО ст ^ь и Л k с СКО ст ^а в выходных сигналах ИИМ и СМС коррекции соответственно. Предполагается малая вариация масштабного коэффициента ИИМ, например | m ( t ) | < 0.01 , когда справедливо 1 - m ² = 1 .

ПОСТАНОВКА ЗАДАЧИ И ПОДХОД К ЕЕ РЕШЕНИЮ

Пусть дискретное измерение ориентации КА с помощью ИИМ, как и измерение угловых скоростей вращения ДМ ^ ps = ^p (ts), выполняется с периодом Tq , калибровка ИММ по сигналам СМС – с периодом To , формирование цифрового управления ДМ – с периодом T ≥ T , а период uq широтно-импульсного управления МП Tum > Tu . Задача состоит в синтезе алгоритмов дискретной фильтрации, цифрового управления кластером ДМ с идентификацией и компенсацией моментов сил сухого трения по осям их вращения, а также алгоритмов широтно-импульсного управления МП при разгрузке кластера ДМ.

Момент сил сухого трения скачком изменяет свое значение при смене направления вращения каждого ДМ, что приводит к проблеме обеспечения требуемой точности стабилизации движения спутника в процессе сканирующей съемки. Для полетной идентификации момента сил сухого трения по оси вращения каждого ДМ предлагается дискретный наблюдатель Луенбергера с периодом Tq . Полученная оценка используется для компенсации этого коварного момента при формировании цифрового управления ДМ. Предлагаются дискретные алгоритмы оригинальной компенсационной схемы для формирования широтно-импульсного управления МП при разгрузке кластера ДМ. Здесь векторные командные сигналы посылаются одновременно как на кластер ДМ, так и на МП, причем эти сигналы равны по импульсу момента на временном периоде m широтно-импульсной модуляции Tu , но имеют противоположные знаки.

КАЛИБРОВКА СОУП

Решение задачи фильтрации измерений, полетной юстировки и калибровки СОУП достигается с помощью двух алгоритмов.

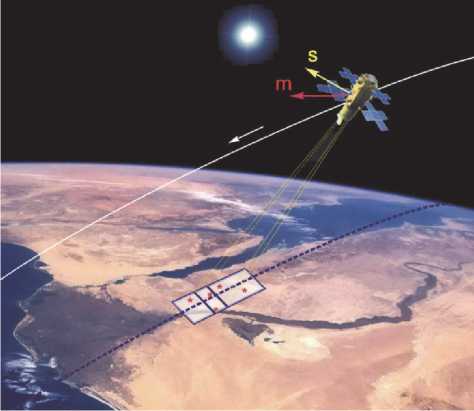
Рис. 1. Схема юстировки СМС

Первый алгоритм реализует юстировку СМС относительно телескопа. Здесь в процессе регулярного наведения бортового телескопа на наземные реперы (рис. 1) для фиксированных моментов времени t_k вычисляются «расчетные» значения орта s направления на Солнце и орта m вектора индукции магнитного поля Земли, а также значения этих же ортов, полученные на основе физических сигналов солнечного и магнитного датчиков. Далее для моментов времени t_k на основе классического алгоритма TRIAD вычисляются угловые положения «расчетного» и «измеренного» базисов в ИСК, выполняется статистическая обработка и получается оценка постоянного кватерниона, представляющего рассогласование их взаимного углового положения.

Второй алгоритм обеспечивает калибровку ИИМ в составе СОУП в отношении дрейфа и масштабного коэффициента, а также юстировку углового положения систем координат, связанных с ИИМ и СМС. Здесь формируются оценки bk, SA и mik, постоянные на периоде To. Полетная идентификация дрейфа ИИМ bg выполняется с периодом To с помощью дискретного нелинейного наблюдателя Луенбергера. Юстировка СОУП и определение оценки П погрешности m масштабного коэффициента выполняются off-line на основе сопоставления значений вектора угловой скорости, которые восстанавливаются автономно по сигналам ИИМ и СМС в одинаковые моменты времени. При аппроксимации значений вектора g to im 5 по методу наименьших квадратов полино-мом5-го порядка ig.to(т) для т = t - kTo е [0,To]

возникает временное запаздывание относительно моментов времени t _k , которое учитывается на основе явных аналитических соотношений.

УПРАВЛЕНИЕ КЛАСТЕРОМ ДМ

Для кластера четырех ДМ принципиальная проблема заключается в распределении векторов

• его кинетического Н и управляющего M = -Н моментов в ССК между избыточным числом ДМ. При некоторых упрощениях эта проблема состоит в одновременном решении двух уравнений

A h = Н V Н е R3, h е R4;

AM = - M ^r = Н ; V M ^r е R ³, M е R ⁴.

Используемый авторский подход к разрешению уравнений (3) основан на применении скалярной функции настройки кластера и позволяет однозначно распределять векторы Н и M ^r = - Н между четырьмя ДМ по явным аналитическим соотношениям.

Введем нормированный вектор КМ кластера h = { x , y , z } = Н / h m = Ah , где x = X j + x ₂ , x , = C y ( h + h 2 ) , x 2 = C Y ( h 3 + h 4 ) ; h = { h_p } , где h p = h _p /h^m и | h_p | < 1 . Распределение этого вектора между четырьмя ДМ выполняется по закону f = x - x + p( x x -1) = 0 , p 12   12

2      2 1/2

где x i = x 1 / q y ; x 2 = x 2 / q_z , q . = ⁽⁴ C y^{- s )} , s = y,z , на основе соотношений

• (i)    q = q y + q_z ; 0 < p < 1 ;

A = ( q / p )(1 - (1 - 4 p [( q y - q_z )( x /2) +

p ( q y q_z - ( x /2)²)]/ q ²)^1/2);

x 1 = ( x + A ) / 2 , x ₂ = ⁽ x ^{- A )} / 2 ;

• (ii)    распределение КМ между ДМ в каждой из двух пар по очевидным явным формулам;

• (iii)    вычисление вектора M ^r по явной формуле M = { m } = ({ A , a f ) ^{- 1}{ - M ^r, - h^mSat( ф p , Ц р f , )} с положительными параметрами ф_p , ц_р и компонентами строки a f = [ a p ] в виде

• 2    C _?    ,                  C ( h ₃ + h ₄)

a f 12 = ^ [2 C y² ± 5 y² h 2 ( h 1 - h 2 )][1 + p ^{Л 3   4}1 ;

q y                                   q_z

• 2    c                   c ( h + h )

a f 3 4 =     [2 C Y² + 5 h 4 ( h 3 - h 4 )][1 + p^^^] .

• q.                                  q y

ИДЕНТИФИКАЦИЯ МОМЕНТА СИЛ СУХОГО ТРЕНИЯ

Для простоты рассмотрим только один ДМ, при этом индекс p не используется. Простейшая модель движения ДМ представляется в нормированном виде Q(t) = a(t) - af(t), где управляющее ускорение a(t) = m(t)/ Jr., ускорение a f( t) = a О Sign(f( t) e [-aО, a О] отра -жает влияние момента сил сухого трения и при известном моменте инерции ДМ Jr параметр a О = m О / Jr = const.

В предположении a ^f ( t ) = a ^f ( t s ) = a ^f = const V t e [ t s , t s _{+ 1} ) для получения оценки a s значения a^f применяется дискретный идентификатор Луенбергера

Я s +1 = П s + ( a s - a ^ S ) T + g f 5Q s ;

a f+i = a f + g p 5Q s ;                     (4)

8^f s +1 = ^f s +1 ^-f s +1

с периодом T q , где постоянные параметры g f и g 2 определяются по явным аналитическим соотношениям. Дискретная оценка момента сил сухого трения получается в виде m ^f ( t_s ) = m s = J _r a s .

ШИРОТНО-ИМПУЛЬСНОЕ УПРАВЛЕНИЕ

Компенсационная схема разгрузки кластера ДМ основана на следующих положениях. Вычисляются модуль Im и орт em вектора потребного импульса механического момента МП в ССК, назначается его вариация AIm на m периоде Tu широтно-импульсного управления МП и рассчитывается постоянная команда Mcu = {mk} =AImem / TUm компенсации им -пульса механического момента МП, которая поступает на кластер ДМ только при включении МП. В моменты времени tr, r e N0 вычисляется орт br = Br IBr и определяется взаимная ориентация ортов br и em в ССК; если | (br,em) | > cos(n/3), то на очередном периоде дискретности МП не включается, иначе вычисляются вектор L = {l.} = AIm(br хem)/Br потребного электромагнитного момента МП, длительности тi = Tumli /1m (если тi > T™ , то тi =: TUmтi/mаx{тi} ) включения МП и знаки компонентов li электромагнитных моментов по каналам.

ЦИФРОВОЕ УПРАВЛЕНИЕ

Пусть задано программное угловое движение КА Л p (t), to p(t), to p(t) в ИСК. Кватерниону рассогласования Е = (e0, e) = Лp ° Л соответствует вектор параметров Эйлера E = {e0, e} и матрица погрешности Ce = 13 - 2[ex]Qe, где Qe = 13e0 + [ex]. Выполняется фильтрация значений вектора £l = -2e0lel рассогласования с периодом Tp и формируются значения вектора £k, k e N0, которые используются в дискретном законе управления

• g k +1 = Bg k + C £ k ; m k = Kg k + P £ k ;

M k = to k x G k + J ( C ek (» P + [ C ek to К x ] to k + m k ).

Здесь Cek = Ce (tk ) , Gk = Jtok + Hk и при обозначениях du = 2/Tu, a = (duтх-1)/(duт1+1) элементы диагональных матриц K , B , C и P вычисляются в виде

b = (duт2- 1Иduт2+ 1);

p = (1 - b ) /(1 - a ) ; c = p ( b - a )

с параметрами т₁ , ^т ₂ и k . Далее вектор M\ + M k ^u с помощью явного закона распределения КМ между 4 ДМ «пересчитывается» в вектор-столбец M _k = { m_pk } управляющих моментов ДМ, которые при добавлении к ним компенсации m_k моментов сил трения фиксируются на полуинтервале цифрового управления с периодом T_u .

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Представленные выше алгоритмы цифрового управления кластером ДМ и широтно-импульсного управления МП были верифицированы на примере малого спутника землеобзора (рис. 2), который располагается на круговой солнечносинхронной орбите с высотой полёта 1200 км, наклонением 100.58 град и долготой восходящего узла 271.35 град. При компьютерной имитации работы СУО применялись такие периоды дискретности: Tq = 1/32 с; To = 1 с; Tp = 1/8 с; Tu = 1/4 с и T™ = 16 с. Схема General Electric минимально-избыточного кластера ДМ представлена на рис. 3. Рис. 4 отображает на карте три маршрута сканирующей съемки с двумя ПМ между ними по крену на углы 30 град. Рис. 5 и рис. 6 представляют программное угловое движение КА в ОСК и компоненты вектора угловой скорости при отсчете времени от начала первого маршрута.

Рис. 2. Малый спутник землеобзора

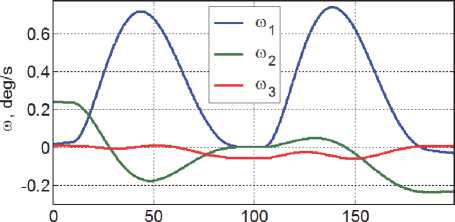
t, s

Рис. 6. Программные угловые скорости

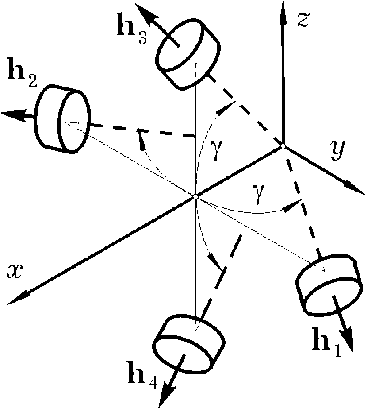
Рис. 3. Схема GE кластера ДМ

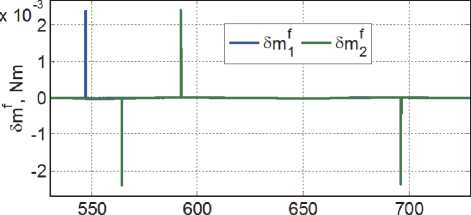
t,S

Рис. 7. Ошибки в оценке моментов трения

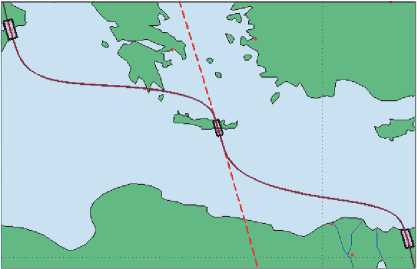
Рис. 4. Отображение маршрутов на карте

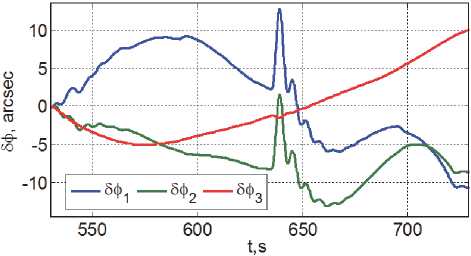
Рис. 8. Ошибки угловой стабилизации

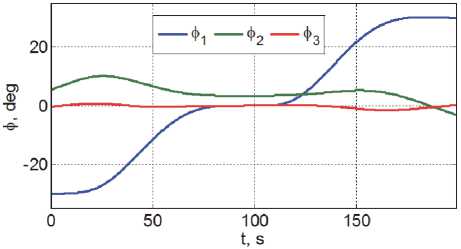
Рис. 5. Программные углы ориентации

вания по углам 5ф i ( t ) и угловым скоростям 8ю i ( t ) при реализации программы углового движения КА, когда измерения СОУП с СМС коррекции используются в расчете вектора рассогласования, который после дискретной фильтрации с периодом T_p применяется для формирования с периодом T_u вектора цифрового управления ДМ с компенсацией моментов сил сухого трения по осям вращения ДМ. Нетрудно убедиться, что кратковременные ошибки в оценке моментов сил сухого трения (см. рис 6) практически не проявляются в рассогласованиях по углам и угловым скоростям движения спутника в процессе выполнения маршрутов сканирующей съемки.

На рис. 10 - 12 представлены компоненты электромагнитного момента МП при широтноимпульсном управлении и соответствующего

На рис. 6 представлены погрешности f ...f        f

δ m_i = m_i - m_i идентификации моментов сил сухого трения для первого и второго ДМ в составе первой пары реактивных двигателей-маховиков.

На рис. 7 и рис. 8 приведены рассогласо- механического момента магнитного привода, а также ошибки угловой стабилизации КА при разгрузке кластера ДМ от накопленного КМ. Последний рисунок демонстрирует эффективность применения предложенной компенсационной схемы.

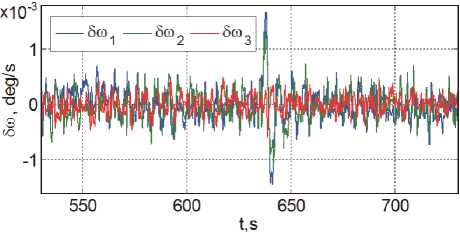
Рис. 9. Ошибки стабилизации скорости

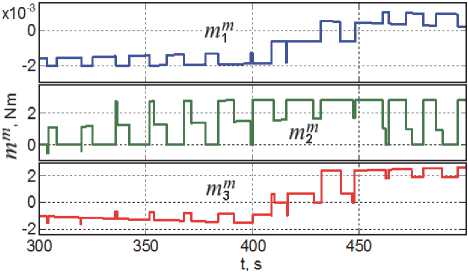
Рис. 11. Механический момент разгрузки

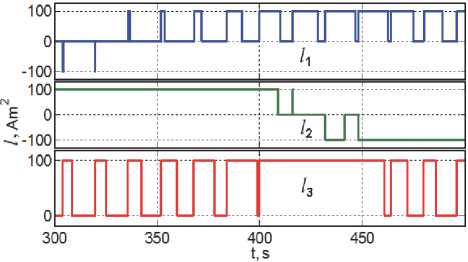
Рис. 10. Электромагнитный момент

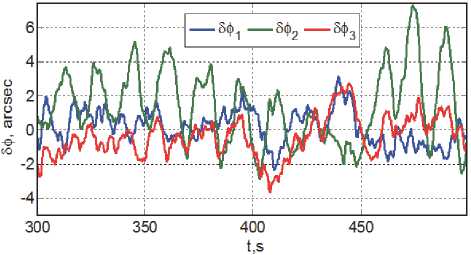
Рис. 12. Ошибки угловой стабилизации

ЗАКЛЮЧЕНИЕ

Кратко представлены решения задач полетной калибровки и юстировки СОУП, идентификации и компенсации моментов сил сухого трения по осям вращения реактивных двигателей-маховиков, синтеза алгоритмов цифрового и широтно-импульсного управления, а также результаты анализа динамики СУО спутника землеобзора при сканирующей съемке и поворотных маневрах.