Цифровое моделирование многолучевого канала связи
Автор: Мишин Д.В., Тяжев А.И.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.17, 2019 года.
Бесплатный доступ
Рассматриваются цифровые математические модели многолучевого канала радиосвязи. В рамках общей гауссовской модели радиоканала описано четырехпараметрическое распределение модуля и фазы комплексного коэффициента передачи радиоканала. Канал с рассеянием характеризуется дискретной многолучевостью, поэтому комплексный коэффициент передачи такого канала представляется в виде суммы конечного числа слагаемых с флуктуирующими коэффициентами передачи и задержками. Сигнал на выходе канала связи представлен через квадратурные компоненты, в которых учтены флуктуации коэффициентов передачи и задержек в канале связи. Эти компоненты в каналах образуются суммированием большого числа слагаемых, когда выполняются требования центральной предельной теоремы теории вероятностей, поэтому их можно считать независимыми нестационарными гауссовскими процессами. Приведены формулы, которые определяют методику моделирования сигнала на выходе многолучевого канала связи. Показано, что, используя четырехпараметрическое распределение амплитуд и фаз принимаемого сигнала, можно осуществить машинное моделирование многолучевого канала с любыми законами замирания сигнала в радиоканале.
Математические модели многолучевого канала, четырехпараметрическое распределение амплитуд и фаз сигнала, цифровое моделирование многолучевого канала
Короткий адрес: https://sciup.org/140255721
IDR: 140255721 | УДК: 621.396.98 | DOI: 10.18469/ikt.2019.17.4.02
Текст научной статьи Цифровое моделирование многолучевого канала связи
Аналитическая модель канала связи позволяет получить достаточно полное представление о свойствах сигналов и помех на входе приемного устройства, дает перечень параметров (в рамках параметрического подхода), определяющих априорную неопределенность ситуации относительно полезного сигнала и мешающих воздействий. Знание модели канала и алгоритмов обработки сигнала позволяет в принципе исследовать качество функционирования системы, количественно определять такие важные характеристики, как вероятность ошибки при приеме дискретных сообщений, среднеквадратические погрешности при оценивании (фильтрации) непрерывных параметров (процессов), время сходимости процесса адаптации и ряд других. Однако чем более подробная аналитическая модель канала используется при таком анализе, тем серьезнее возникают трудности математического характера, не позволяющие достичь приемлемого результата.
Выход из создавшейся ситуации может быть найден при использовании одного из методов математического моделирования, а именно метода статистических испытаний, реализуемого с применением ЭВМ.
Процессы в системах связи обладают рядом специфических свойств, главными из которых являются их статистическая природа и высокая скорость протекания. Эти свойства порождают ряд проблем статистического моделирования на ЭВМ: адекватное описание непрерывных случайных процессов в дискретном времени, разработка максимально экономных моделирующих алгоритмов, стремление к проведению исследований в реальном масштабе времени.
Очень часто на качество работы приемной части цифровой системы связи влияют так называемые глубокие замирания сигнала в многолучевом канале связи. Под замиранием понимаем непрерывное и беспорядочное изменение уровня сигнала. Физической причиной замираний является главным образом изменение параметров среды распространения (неоднородность), многолучевое распространение (за счет любых отражений, порождающих эхо-сигналы), наличие энергоемких (реактивных) элементов в тракте передачи, возможные доплеровские эффекты [1-6].
Модель канала и сигнала на его выходе с использованием квадратурных представлений
Будем рассматривать преобразование сигнала в многолучевом радиоканале, используя представление сигнала на входе канала комплексной функцией t/(z):
й^ = и^еМП. (1)
Действительный сигнал на передаче при этом записывается в виде
m(z) = (/(/) cos[®0Z + 6(z)], (2)
где 17(z) и 0(z) отражают соответственно наличие в сигнале амплитудной и угловой модуляции или учитывают временное рассеяние сигнала, связанное с внесением в него предыскажений при формировании заданной формы спектра сигнала в канале. Процессы t/(z), 9(z) изменяются по сравнению с колебанием частоты ю0, как правило, настолько медленно, что сигнал и^ можно считать узкополосным.
Квадратурные компоненты сигнала U (z) могут быть записаны как
^(Z) = t7(z)cos0(z), Mv(z) = Z7(z)sin 6(z).
Передаточную функцию (ПФ) канала связи можно также записать через квадратурные компоненты [7]:
Я(/, z) = x(/, z) + jy(/, z) =
= 7(Л t)e — модуль ПФ; /, Л ^(/Я) - аргумент ПФ; ^(/Я) = у(/Д) cos(p(/,z), Н/Я) = уС/Я) 8Й1ф(/д) — квадратурные компоненты ПФ, которые являются соответственно четной и нечетной функциями частоты/ Для большинства реальных каналов связи квадратурные компоненты т(/,?) и у(/,?) являются медленно меняющимися (по сравнению с cos cooZ) функциями времени. Поэтому, не нарушая общности, можно записать: х(/,?) = х(?), y(j,t) = y(t), y(/t) = y(0’ ф(Л0=ф(0- Канал с рассеянием будем характеризовать дискретной многолучевостью так, что комплексный коэффициент передачи канала на частоте <в0 может быть записан в виде KU®0,t) = ^7, (0е'М’т', (5) /=1 где у, (?) и т, - флуктуирующий коэффициент передачи и задержки /-го луча, / = 1,2,...,Т. С учетом (1) и (5) сигнал на выходе канала связи может быть представлен как У(?) = ^(?)^(уЮо,?) = Л (6) = ^[/(?)у,(?)е-,[е('-т')-ю"т'], /=1 где у, (?) = %,(?)+ ./>,(?). (7) Здесь х, (?) и у, (?) - квадратурные компоненты комплексного коэффициента передачи /-го луча. Сигнал на выходе канала связи S (?) также может быть представлен через квадратурные компоненты S^ = SxWjSy^, (8) которые для действительного сигнала определяют так: 5 (?) = ^ (?) cos ш0? - 8у (?) sin ю0?. (9) После несложных преобразований (6) получа ем следующее представление выходного сигнала по квадратурным компонентам: L Sx (?) = ^^х, (0[м* (? _ ч) cos®oT + /=1 + г/Д?-т,) sinto0T,]- (]0) -у, (?) [wv (? - tz ) sin ®otz - -г/Д?-т,) COStogT,]}, L sy = sin®oT/ - /=1 -uy(?-T,) cosco0t,] + ^^ + у, (/)[ыт (?-T,) COSCOqT, + + uy(?-t,) sincDgT/^. Формулы (10), (11) определяют методику моделирования сигнала на выходе многолучевого канала связи. Задаваемые достаточно произвольно параметры L, т, определяют характер межсимвольной интерференции на выходе канала, а случайные процессы х, (?) и у, (?) определяют режим замираний сигнала. Число отсчетов сигнала S (?) на длительности тактового интервала Т определяется числом отсчетов сигнала w(?). В некоторых каналах как проводной, так и радиосвязи с медленными изменениями параметров квадратурные компоненты можно считать детерминированными на конечном интервале анализа Та = [0, Г]. где Т - длительность сигнала и (?) на передаче. Общая гауссовская модель Чаще всего, особенно в каналах радиосвязи, канал приходится считать стохастическим с той или иной вероятностной моделью для х и у. Учитывая, что эти компоненты во многих каналах образуются суммированием большого числа слагаемых в условиях, когда выполняются требования Центральной предельной теоремы теории вероятностей, их при данном L можно считать независимыми, в общем случае нестационарными гауссовскими процессами с математическими ожиданиями и корреляционными функциями ™х„ (О’ ШуЛ^’ Kxk{f^Y КуЛ^1\ Исходя из физических соображений и экспериментальных данных можно считать, что коэффициенты корреляции у квадратурных компонент одинаковы ^t 01 ’ ^2 ) =Ryt (^1 ’ ^2 ) = ^ (^| Тг ) • Очень часто [2; 3] коэффициент корреляции аппроксимируется показательным законом (по каждой из переменных): R (aA = R (А?) = е"“Н, А J ’ (12) а > 0, А? = ?2 - ?,. Аппроксимация (12) при гауссовском распределении означает, что процесс является одномерномарковским. Таким образом, общая гауссовская модель описывается следующими параметрами: ^(0, <(0, <(0’ М^лУ Четырехпараметрическое распределение В рамках описания одномерными распределениями вероятностей коэффициента передачи у рассмотренная модель (9) характеризуется двумерной четырехпараметрической плотностью вероятности квадратурных компонент [7]: ^2(чт) = -—77—(13) ^xVPyV) x exp« В этом случае четырехпараметрическое распределение модуля и фазы передаточной функции имеет вид где со8фтЛ.ст2 - зшфщ ст2 <5xC5yJ(32y COS2 ф + ст2 sin2 ф 10 (х) - модифицированная функция Бесселя нулевого порядка; - функция Крампа. Экспериментальные данные в радиоканалах различных диапазонов подтверждают возможность удовлетворительной аппроксимации распределений амплитуд и фаз, как общим четырехпараметрическим законом, так и его частными случаями, к числу которых относятся следующие варианты. 1. Трехпараметрические замирания (тх = 0). 2. Райсовские (обобщенно-релеевские) замирания (ст2 = ст2 = ст2, тх +ту * 0). 3. Подрелеевские замирания (т. = mv = 0). Наиболее глубокие замирания соответствуют случаю одностороннего-нормального распределения (тх = т = 0, ст2 = 0). 4. Релеевские замирания (тх = ту= 0). 5. Канал без замираний (ст2 = ст2 = 0). В подавляющем большинстве реальных каналов связи параметры тх, т , ст2, ст2 можно считать не зависящими от t. Скорость замираний квадратурных компонент х(?), у(?) определяется характером коэффициентов корреляции К^,12У Большую часть каналов, удовлетворительно описываемых моделью (10), (11), можно отнести к категории каналов с медленными (неселективными) замираниями, когда коэффициент корреляции R^t^t^ близок к единице. При моделировании канала связи, основанного на представлении выходного сигнала в виде (10), (11), можно задавать характер межсимвольной интерференции на выходе канала с помощью достаточно произвольного выбора параметров L, г,. Обычно г, берут кратным Т (длительности тактового интервала), в этом случае N характеризует количество отсчетов импульсной характеристики канала. Режим замираний определяется с помощью представления yt (?) и ф4 (?), параметров тх, т , ст2, ст2. Таким образом, используя четырехпараметрическое распределение амплитуд и фаз принимаемого сигнала, легко осуществить цифровое моделирование многолучевого канала на ЭВМ с любым законом замирания. Цифровое моделирование многолучевого канала Для этого необходимо задать начальные значения отсчетов импульсной характеристики канала Go = (g,}, i = 0, N -1, выбрать характер замираний. С этой целью устанавливают значения элементов взаимокорреляционной матрицы лучей Rip i,j = Q,N — \, следующим образом: для общих замираний Rtj —> 1; для селективных замираний -1 < RM< 1. В обоих случаях RH = 1. Далее формируют последовательность коррелированных случайных величин г](и), и = 1,2,... с четьтрехпараметриче-ским законом распределения с параметрами тх, mv, ст2, ст2 и коэффициентом корреляции вида (12) методом скользящего суммирования в виде разностного уравнения: П 00 = ^р.^ + р2^, (17) ^ОО^хОО + б.^О?-!), р2 (и) = а2у^ + Ь2р2 (и -1), где х(и), у (и) - последовательности независимых нормальных случайных величин с параметрами тх, ту, ст2, ст2; а параметры рекуррентного алгоритма ах, а2, Ьх, Ь2, связанные с р, определяются на этапе предварительной подготовки к моделированию аналогично [8-10]. Начальные условия в рекуррентных уравнениях (18), то есть предыдущие значения последовательности р(и) при вычислении первого элемента этой последовательности можно выбрать нулевыми. При этом будет иметь место некоторый переходный процесс, в результате которого начальный участок моделируемого процесса окажется искаженным. Однако после окончания переходного процесса последовательность т](и) становится стационарной. В [8] отражено влияние начальных условий на протяженность переходного процесса. Таким образом, последовательность значений вектора отсчетов импульсной характеристики многолучевого канала с общими замираниями определяется как G„=Gon(«), и = 1,2,... (19) Для канала с селективными замираниями учет взаимной корреляции между отдельными лучами можно сделать в соответствии с [8] методом канонического разложения или методом линейного преобразования. Число отсчетов сигнала S^ из (19) на длительности тактового интервала Топределяется количеством отсчетов сигнала и^. Так, например, при моделировании передачи двоичных сообщений с использованием фазовой модуляции с Аср = ±тг символу «+1» соответствует сигнал и^ = Uo sincooZ, символу «-1» соответствует сигнал w(?) =-t/0 sinco0T где Uo - постоянная амплитуда. Квадратурные компоненты при этом для UQ sin mot определяются как и, (z) = 0, и (z) = [70 и для противоположного сигнала m(z) = —Uo sinto0Z wi(z) = 0, г/ (z) = -£70. Переход к дискретному времени при представлении данного сигнала отсчетами м(СУ) может быть осуществлен в соответствии с теоремой Котельникова с учетом выбранного значения скорости передачи. Так, например, при сигнале ФМ и скорости передачи И = 1600 бит/с для значения F = 400 Гц получаем Az = 1/2Е = 7/4. Таким образом, для приведенного примера полосовому сигналу соответствует 4 отсчета или 2 отсчета на каждую квадратурную компоненту. Заключение Используя описанные выше методики, можно получить выражение для сигнала и (z) и его квадратурных компонент при более сложных видах модуляции. Отметим, что представленные математические модели многолучевого канала радиосвязи являются вполне адекватными для большинства реальных каналов связи и, что самое главное, хорошо приспособлены для проведения статистического имитационного моделирования.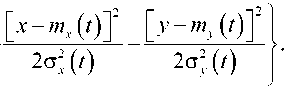
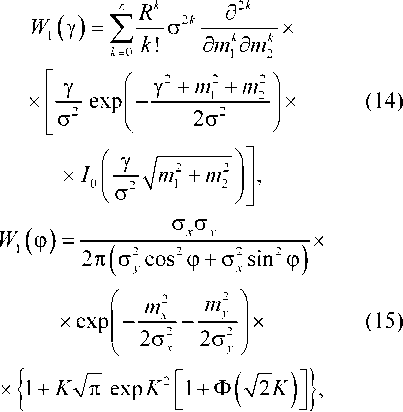
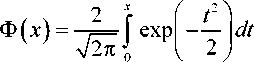
Список литературы Цифровое моделирование многолучевого канала связи
- Кеннеди Р. Каналы связи с замираниями и рассеянием / пер.с англ. М.: Сов. радио, 1973. 304 с.
- Кловский Д.Д. Передача дискретных сообщений по радиоканалам. М.: Радио и связь, 1982. 304 с.
- Карташевский В.Г., Мишин Д.В. Прием кодированных сигналов в каналах с памятью. М.: Радио и связь, 2004. 239 с.
- Мишин Д.В. Методы повышения эффективности обработки сигналов в каналах с памятью: дис. … д-ра техн. наук. Самара, 2004. 386 с.
- Финк Л.М. Теория передачи дискретных сообщений. М.: Связь, 1970. 728 с.
- Мишин Д.В. Итерационная процедура вынесения решения в канале с памятью при совмещении операций демодуляции и декодирования // Физика волновых процессов и радиотехнические системы. 2003. Т. 6. № 4. С. 79-84.
- Кловский Д.Д., Конторович В.Я., Широков С.М. Модели непрерывных каналов связи на основе стохастических дифференциальных уравнений. М.: Радио и связь, 1984. 248 с.
- Быков В.В. Цифровое моделирование в статистической радиотехнике. М.: Сов. радио, 1971. 328 с.
- Иванова В.Г., Тяжев А.И. Цифровая обработка сигналов и сигнальные процессоры. Самара: Офорт, 2008. 264 с.
- Карташевский В.Г. Обработка пространственно-временных сигналов в каналах с памятью. М.: Радио и связь, 2000. 272 с.


