Цифровое управление кластером шести гиродинов при начальной ориентации космического аппарата

до номинального значения h _g их собственного кинетического момента (КМ) лишь для пар ГД.

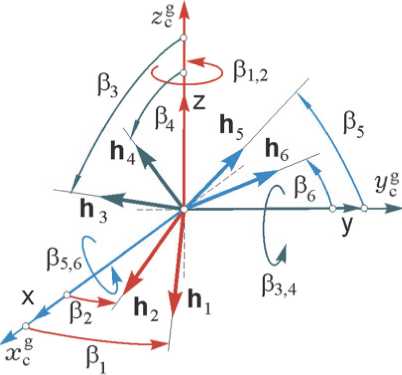
Рис. 1. Отсчет углов ГД в СГК по схеме 3-SPE

После отделения от ракеты-носителя КА начинает кувыркаться – вращаться с вектором угловой скорости ω изменяемого направления в базисе B , связанного с его корпусом. Здесь выделяются следующие режимы начальной ориентации: (i) успокоение (остановка вращения) КА в инерциальном базисе с помощью МП; (ii) накопление измерительной информации, перевод ориентации КА к требуемой и стабилизация его положения c минимизацией усредненного за виток ССО углового рассогласование ϕsp = arccos〈np,s〉 между ортом np к плоскости панелей солнечных батарей (СБ) и ортом s направления на Солнце с помощью МП и одноосного привода панелей СБ, когда выполняется разгон роторов гиродинов и приведение СГК парковое состояние; (iii) включение СГК в кон- тур управления, автономное угловое наведение и управление КА с приведением его ориентации к заданной в орбитальном базисе O и последующей угловой стабилизацией.

В нашей статье [1], публикуемой в этом же номере журнала, аналогичная задача исследована для КА, управляемого минимально-избыточным кластером реактивных двигателей-маховиков, где отсутствует необходимость предварительного разгона их роторов, и, следовательно, длительной ориентации панелей СБ на Солнце для энергетического обеспечения такого разгона.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Инерциальными системами координат (ИСК), используемыми для описания перемещения центра масс и углового движения КА, являются геоцентрическая экваториальная система координат (СК) I _⊕ (O _⊕ X^I_eY_e^IZ_e^I ) и солнечноэклиптическая СК I _s(O_sX_s^IY_s^IZ_s^I) , рис. 2.

Начало ИСК I _⊕ расположено в центре Земли O _⊕ , ось X _e ^I направлена в точку весеннего равноденствия ϒ , а ось Z _e ^I – на Северный полюс мира P _N по оси суточного вращения Земли с угловой скоростью ω _e . ИСК I _s имеет начало в центре Солнца O _s , ее ось X _s ^I также направлена в точку ϒ , а оси Y _s ^I и Z _s ^I получаются поворотом соответствующих осей Y _e ^I , Z _e ^I на угол ε _e относительно оси X ^I _e (X _s ^I ) . Угол ε _e между плоскостями земного экватора X _e ^I O _⊕ Y _e ^I и эклиптики X _s ^I O _s Y _s ^I равен 0.41015234 рад (23.44 град), см. рис. 1. В ИСК I _⊕ орт e _s направления из центра Солнца к центру Земли имеет вид e _s ^I ( t ) = [ -ε _e ] ₁ [ -ρ _s ( t )] ₃ {1,0,0} , где ρ s ( t ) = ρ s ⁰ +ω s ( t - t ₀ ) , ρ s ⁰ =ρ _s ( t 0 ) , t ₀ – некоторый начальный момент времени, ω _s = 0.19965 ⋅ 10^-6

с^-1– средняя угловая скорость обращения Земли вокруг Солнца в плоскости эклиптики за тропический год (365.2422 средних солнечных суток). Здесь и далее используются общепринятые обозначения { ⋅ } = col( ⋅ ) , [ ⋅ ] = line( ⋅ ) , 〈⋅ , ⋅〉 , ( ⋅ )^t , [ a x ] и ° ,~ для векторов, матриц и кватернионов, матрицы [ α ] _i элементарного поворота вокруг i -ой оси на угол α , i = 1,2,3 ≡ 1 ÷ 3 , а также C _α ≡ cos α , S _α ≡ sin α . Астрономическая долгота Солнца λ _s , которая определяется в ИСК I _⊕ как угол между направлением на точку весны ϒ и ортом s = - e _s направления от центра Земли к центру Солнца, вычисляется по формуле λ _s ( t ) =π+ρ _s ( t ) .

Применяется геодезическая Гринвичская система координат (ГСК) G (O _ffi X^eY^eZ^e) , связанная с Землей, которая вращается с угловой скоростью ω _e = 7.2921158 . 10^-6 с^-1. Положение ГСК E относительно ИСК I _⊕ определяется углом ρ e ( t ) =ρ e ⁰ +ω e ( t - t 0 ) , где ρ _e ⁰ =ρ _e ( t ₀ ) – угловое положение Гринвичского меридиана относительно направления на точку ϒ при t = t ₀ и ω _e - модуль вектора M _e = {0,0, W _e } угловой скорости вращения Земли. Преобразование векторов-столбцов расположения r _o и скорости v _o поступательного движения ЦМ O КА из ИСК I _⊕ ( r _o ^I , v _o ^I ) в ГСК G ( r _o ^G , v _o ^G ) выполняется по соотношениям r G = [ Р е ] з r ; V о = ^{- [ m} e ^{x ][} P eL r O + [ P e ]₃ V { , а обратное преобразование – по соотношениям Г О = М Г ; V = [ P e ] 3 ( v : + M. Х ] Г _О ° ) .

Плоскость орбиты КА в ИСК определяют долгота восходящего узла Ω_{^ o} и наклонение i _ο , см рис. 3. Положение центра масс КА на эллиптической орбите с эксцентриситетом e _o определяется вектором r _o ( t ) и истинной аномалией ν _o ( t ) , отсчитываемой от перигелия орбиты π , который находится на угловом расстоянии ω_π от ее восходящего узла в направлении движении ЦМ.

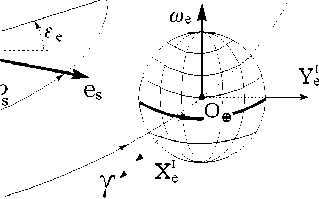
Рис. 2. Инерциальные СК

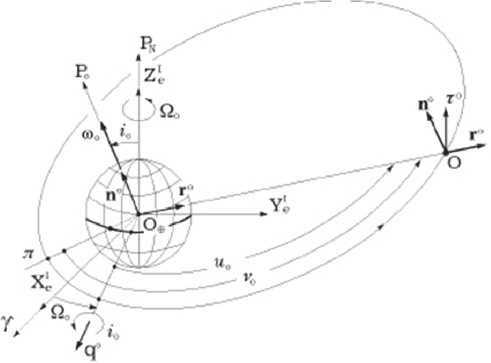
Рис. 3. Орбита КА и орбитальная СК

Орбитальная система координат (ОСК) O (Oxoyozo) с началом в центре масс КА O и ортами o1 ,o2 , o3 имеет следующие направления осей и связанных с ними ортов: ось Oyo и орт o2 совпадают по направлению с ортом r o вектора rο (t); ось Ozo и орт o3 = -no направлены o противоположно орту нормали n к плоскости орбиты; ось Oxo с ортом o1 дополняет ОСК до правой – принадлежит плоскости орбиты, перпендикулярна оси Oyo и направлена в сторону орбитального движения центра масс КА. Вектор угловой скорости ωo орбитального движения ЦМ КА определяется как шо = шо(t)по = vo(t)n0.

Геомагнитная СК M (O ⊕XmYmZm) определяется с помощью вектора магнитного момента M⊕ =M⊕m⊕ магнитного поля Земли (МПЗ) с модулем M⊕ следующим образом: ось O⊕Zm направлена по геомагнитной оси с ортом m⊕ , фиксированным в ГСК, а ось O⊕Xm – по линии пересечения геодезического и геомагнитного экваторов. В простейшем случае МПЗ в точке O представляется магнитным потенциалом ди- поля, когда вектор индукции магнитного поля Земли B = Bb с модулем B = µem M⊕aom /ro3(t), m где µe – магнитная проницаемость вакуума и aom – модуль вектора aom =m⊕ - 3〈m⊕,ro〉ro , который направлен по орту b = aom / aom

Используется связная с корпусом КА система координат (ССК) B (O xyz ) (body) с ортами b _i , направленными по соответствующим осям ССК. Ориентация ССК B в ИСК I _⊕ определяется кватернионом Λ = ( λ₀, λ ) , где λ = { λ _i } , вектором параметров Эйлера Λ = { λ₀, λ } , который представляется в форме Л = { С _ф /2 , e S _ф /2 } с ортом e мгновенной оси Эйлера и углом Φ собственного поворота, а также вектором модифицированных параметров Родрига (МПР) О = { о i } = е tg( Ф / 4) , который связан с кватернионом Л прямыми О = Х / (1 + X ₀ ) и обратными X ₀ = (1 -о ²)/(1 + о ²), Х = 2 о /(1 + о ²) соотношениями.

Связанная с панелями СБ система координат (РСК) P (O^p x ^p y ^p z ^p) определяется так: ось O ^p y ^p и орт p ₂ совпадают по направлению с нормалью n ^p к плоскости фотоэлементов панелей СБ, ось O^p z ^p и орт p ₃ совпадают по направлению соответственно с осью O z и ортом b ₃ ССК, а ось O^p x ^p дополняет РСК до правой ортогональной. Угловое положение панелей СБ относительно ССК определяется углом γ ^p ≡ γ их поворота вокруг оси O z ССК. В парковом положении панелей СБ на корпусе КА угол

γ ^p = 0 , при этом направления осей РСК и ССК совпадают.

При составлении модели движения спутника начало ССК (точка O ) считается полюсом, который совпадает с центром масс КА при не-деформированном состоянии его конструкции. Кинематические соотношения для кватерниона Λ и вектора МПР ^σ имеют соответственно вид

Л = Л о ш/ 2;

о = |(1 - о ²) го + 2 о х го + 2 ( о , го ) а , динамика углового движения КА описывается уравнением

J ( Y )(b = -rox G + M p + M m + M ^g + M ^d . (2)

Здесь G = J ( y ) ®+ H является вектором КМ электромеханической СУО, где столбец H = { Н i } представляют КМ СГК; вектор M ^g = {M _i ^g } управляющего момента СГК формируется в виде М ⁸ =- H , где ( ⋅ )^* – символ локальной производной по времени; to = { to i } - вектор абсолютной угловой скорости КА, представленный в ССК O xyz ; J ( γ ) = J ^o + 2 J ^p( γ ) – тензор инерции КА при произвольном положении панелей СБ, при этом изменяемая часть тензора инерции каждой панели СБ в ССК представляется в виде

J ^P( Y ) =

j p с ; +j^; j^p_x ; c _Y ^ _Y

J? C V 5 _Y j p 5 V ² + j p c ²

где Jpx , Jpy и Jzp – собственные моменты инерции каждой панели в ее центре масс и J xpyd =Jxp -Jyp ; столбец мР = {(jp;($2,ro, -C2,^2)-2jp^2)Y,

- (jp;(C2,^1 -S2,^2) + 2JZPШ2)Y, -2JP y} представляет вектор момента инерционно-гироскопических сил из-за подвижности двух панелей СБ; Mm = {mim} – вектор управляющего механического момента магнитного привода (МП), а вектор Md представляет внешние возмущающие моменты. Вектор управляющего механического момента МП формируется по формуле Mm = {mim} = -L × B, где вектор электромагнитного момента (ЭММ) L = {li} с ограниченными компонентами | li | ≤ lm и вектор индукции магнитного поля Земли B с ортом b определены в ССК.

Вводятся также ортогональная гироскопическая система координат (ГСК) Oxcgycgzcg силового гироскопического кластера, для простоты совпадающая с ССК Oxyz, отсчет углов ГД вp относительно осей их подвеса, см. рис. 1, и обозначения проекций ортов КМ каждого ГД на оси системы координат СГК х1 = С] - cosР]; x2 = C2 - cos в2; y, = S, - sinв1;

y ₂ = S ₂ - sin в ₂ ; x ₃ = S ₃ - sin P ₃ ; x ₄ = S ₄ - sin P ₄ ;

z 3 C з = ГО^ ^; z 4 — C 4 ^{— cos в} 4 ^; y 5 C 5 = ^cosP ₃ ^;

y 6 = C 6 = ^cos 3 ₆ ; z 5 = S 5 = ^sin p 5 ; z 6 = S 6 = ^sin& •

f , j ( P ) - X j2 — X 34 +p (X j2 X 34 — 1);

f , 2 ( P ) - X 56 - X 12 + P (X 5s X 12 - J);

f , 3 ( P ) - ^X 34 - ^X ₅ 6 +P (^X 34 ^X 56 — 1),

Тогда вектор нормированного кинетиче-

ского момента СГК h® — Н ( в ) /К , , где столбец р = { в p } , p = 1 ^ 6 , и градиентная матрица A _h ( Р ) = 5 h / д р представляются в виде

где постоянный параметр p удовлетворяет условию 0 < p < 1. Для представления условий однозначной разрешимости уравнения h(P) = h, где h = {x, y, z} является известным столбцом, относительно синусов и косинусов углов в p всех шести гиродинов, вводятся обозначения p12 = V4 — (x12 ) ; q12 = V4 — (y 12 ) ;

A h ( P ) =

	x		" C 1 + C 2	+ S 3	+ S 4
h =	y	=	S 1 + S 2	+ C 5	+ C 6
	. z .		. C 3 + C 4	+ S 5	+ S 6 .

^- S 1

C i

- ^S 2

C 2

C 3

C 4

0    - S 5

-

S 6

^p 34 = V^{4 — ( z} 34 ⁾ ; q 34 = V^{4 — ( x} 34 ⁾ ;

p 56 = j ^-y ^y lef ; q 56 = ^A- z y^ Ief ;

x12 _ x + A x , _x-Ax . _ =У + A У ; 2    ; x34 2 ; x56 2 У -Ay z + A       z -A z z y12 ~    ; z 34 ; z56 ; 2 2 2 dx = 912 + P34; dy = q56 + P12; dz = q34 + P56^

- ^S 3

- ^S 4

C 5

S

Вектором цифрового управления СГК

и , ( t ) — {и ®, ( t )} ^с периодом T u , u pk ⁽ t ⁾ = u pk V t ^g [ t k , t k + 1 ) , 4 + 1 = tk ⁺ T_u , k g N ₀ , считается вектор P _k - { P _pk } — и g скоростей ГД относительно осей их подвеса с ограниченными по

модулю компонентами | в ( t )| <в m , кусочнонепрерывный управляющий момент СГК фор-

мируется по соотношениям ■

M g ( t ) = - h _g A h ( p ( t ) u g ( t ) ; P ( t ) = u g ( t ) . (3)

Сингулярные состояния этой схемы возникают при таких угловых положениях ГД, когда матрица Грамма G ( p ) = A h ( P ) A h ( P ) теряет полный ранг, т.е. при G = det( G ( p ) = 0 . Важной проблемой управления СГК избыточной структуры является выбор функции распределения вектора КМ СГК между ГД - закона настройки СГК. Наиболее рациональными [2] являются явные законы настройки, когда все характеристики движения ГД получаются по аналитическим соотношениям. При обозначениях

Условия разрешимости векторного уравнения h ( P ( t ) = h ( t ) имеют вид

A _x = d x {1 - [1 - 4 p (( q 12 - p 34 )( x /2)

+ p ( q 12 p 34 - ( x /2) ² ))/ d^}/ P ;

A_y= dy {1 - [1 - 4 p (( q ₅₆ - p_{x 2})( y /2)

^{y y}                                           (3)

+ p ( q 56 P 12 - ( y /2) ² ))/ d^T}/ p ;

A _z = d z {1 - [1 - 4 p (( q 34 - p 56 )( z /2)

+ p ( q 34 p 56 - ( z /2) ² ))/ d^T}/ P

и при введении столбца A = { A _x , A y , A _z } очевидным образом преобразуются к нелинейному векторному уравнению A = Ф ( h , A ) . Получить аналитическое решение этого уравнения для определения углов в*, ГД при парковом состоянии СГК весьма затруднительно, но его

x_j2 = x _j + X ₂ ; X ₃₄ = X ₃ + X ₄ ;

y j2 = y j ⁺ y 2 ;

y 56    y 5 ⁺ y 6 ; ^z 34    ^z 3 ^{+ z} 4 ; ^z 56    ^z 5 ^{+ z} 6 ;

численное решение достигается практически мгновенно по методу простой итерации - при рациональном выборе начального точки достаточно лишь 2-3 итераций для получения результата с приемлемой точностью.

Далее при введении обозначений

X

^X 12

X

; ^X 34

^X 34      ~        y 12

Д-Ж ’ y ¹² = 4 < ’

а₁ =

x + A _x 2

b1 =

2-^. ;

С 1 = a^a i + ^b1 ;

^X 12

V^{4 -} y ²

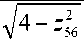
. X

; ^z 34

^Z 34

^^^^^^^.

X ²

^X 34

-

z

_____ 56

V⁴ - y 56

d 1 = V 4 - C 1 / С 1 ;

a ₂ =

z + A _z

■ b = x -A x

’ 2       2

и компоненты явного векторного закона настройки f p ^{( p )} = ^{ f p i , f _{) 2} , f ^} = 0 СГК схемы 3-SPE принимаются в виде [2]

I 2    2 I 2           У + A

c? = Л/a9 + bx ; d9 = Л/4 - c9 /c9; a, =------:

2          2      2      2               2     2    3

^b 3 =

z-A z

c 3 — yj a 3 + b 3 ; d 3 — 4 — c 3 / c 3

вычисление синусов и косинусов углов β _p всех шести ГД выполняется по явным аналитическим соотношениям

1-я пара (ГД 1 и ГД2):

x i =

a₁ - d ₁ b₁

b + da y i = "T"

. _v _ ^a i ^{+ d} i b i

; x 2 =

b - da

’ y 2 = —;—;

b + d₂a₂ x з = ~         ’

2-я пара (ГД3 и ГД4):

z 3 =	a 2 - d 2 b 2        b2	— d 2 a 2	’ z 4	_ a 2	+ d 2 b 2
	~     2      ’ x 4 = пара (ГД5 и ГД6):	2		— d 3 b	2
			a 3
3-я
		y 5 =		2	’
z 5 =	b3 + d 3 a 3        a 3	+ d3b3	; z 6	= b 3"	— d 3 a 3
	-     2      ' y - =	—— 2			• 2

Положение нечетных ( p = 1,3,5) и четных ( p = 2,4,6) ГД в трех парах i = 1 - 3 удобно представить углами a i = ( в ₂ i _{- 1} + в ₂ i )/2 и 5 i = ( в ₂ i _{- 1} - в ₂ i ) / 2 , i = 1 - 3 , которые поясняют применяемое выше наименование «ножничной пары» – угол α _i определяет центральную линию a_i «ножниц», а углы ± δ _i – положения векторов КМ h ₂ i _{- 1} и h ₂ i относительно линии a i в i -ой паре ГД. Парковое состояние СГК, которому соответствует значение вектора его КМ H = Σ h _p = 0 при h p = | h p | = h _g , приведено на рис. 4. Здесь векторы КМ всех 3 пар ГД h i = h ₂ i _{- 1} + h ₂ i с одинаковыми модулями и концами в точках A , B и C принадлежат плоскости P , которая содержит начало O системы координат СГК, причем векторы h _i направлены по линиям a_i .

Детальный топологический анализ сингуляр -ных состояний схемы 3-SPE и проходимости внутренних сингулярных поверхностей данной схемы показывает [2], что все эти поверхности проходи-

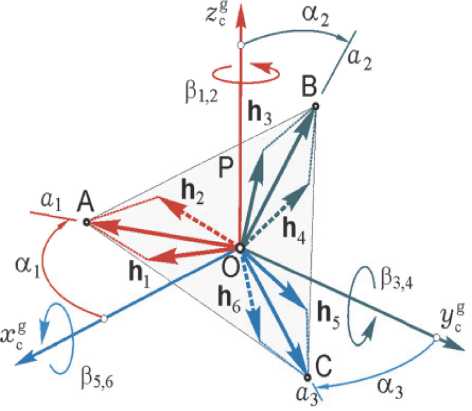
Рис. 4. Парковое состояние СГК мы . При этом наибольшую сложность в исследовании доставляет именно начало ГСК – центра сгустка сингулярных поверхностей, см. рис. 5.

Явный векторный закон настройки СГК принимается в виде

Aр (в) в = -Ф(в) = - sat(фр, црfp (в)), (4) где матрица Лр (в) = дfp (в) / дв   и векторная функция sat(фр,Црfp(в)) = {sat(фр, Црf,,-(в)) , i = 1 - 3 имеет параметры ограничения φρ и усиления µρ . Данный закон настройки обеспечивает отсутствие сингулярных состояний СГК по схеме 3-SPE для всех внутренних точек области S вариации вектора его суммарного кинетического момента. Здесь рационален выбор параметра ρ = 0.65.

При известном значении вектора M ^g управляющего момента СГК вектор цифрового управления всеми шестью ГД u ^g = 0 q рассчитывается так: сначала вычисляется вектор

Р q =- ({А ьф)), Ар ф)) })-1{Мg/h g, Ф (Р )} и затем с учетом условия max | Рqpk | <Рm формируется вектор цифрового управления ГД ■ u д=в q.

Бесплатформенная инерциальная навигационная система (БИНС), корректируемая сигналами навигационных спутников ГЛОНАСС/ GPS и звездных датчиков, измеряет в моменты времени t_{T + 1} = t _l + T _p , l е N ₀ = [0,1,2,3...) как векторы расположения и скорости поступательного движения центра масс КА, так и кватернион его ориентации, которые преобразуются в их значения относительно ИСК I _@ по аналитическим соотношениям.

При определении ортов r ^o = r _o / r_o и v ^o = v _o /v _o положение ортов o ₁ , o ₂ и o ₃ ОСК O в ИСК I _@ вычисляется на борту КА по алгоритму

0 3 = ( r ^o X v ^o )/1 r ^o X v ^o | ; o ₂ = r ^o ; o ₁ = o ₃ X o ₂ .

Пусть в моменты времени t_s с периодом T _q , t s ₊ 1 = t s + T _q , s е N ₀ с помощью магнитометра измеряется вектор индукции МПЗ B = B b , а в моменты времени t_r с периодом T m , t r _{+ 1} = t r + T u ^m, ^r е N ₀ формируется цифровое управление МП, когда значения компонентов вектора ЭММ L = {l i ) фиксируются V t ^е [ t r , t r + 1 ) . Цифровое управление СГК формируется в моменты времени t_k с периодом T _u , t k + , = t k + T , , k е N , .

Задача статьи состоит в (i) анализе процесса успокоение КА в ИСК с помощью МП; (ii) применении авторских алгоритмов автономного наведения и управления ориентацией КА

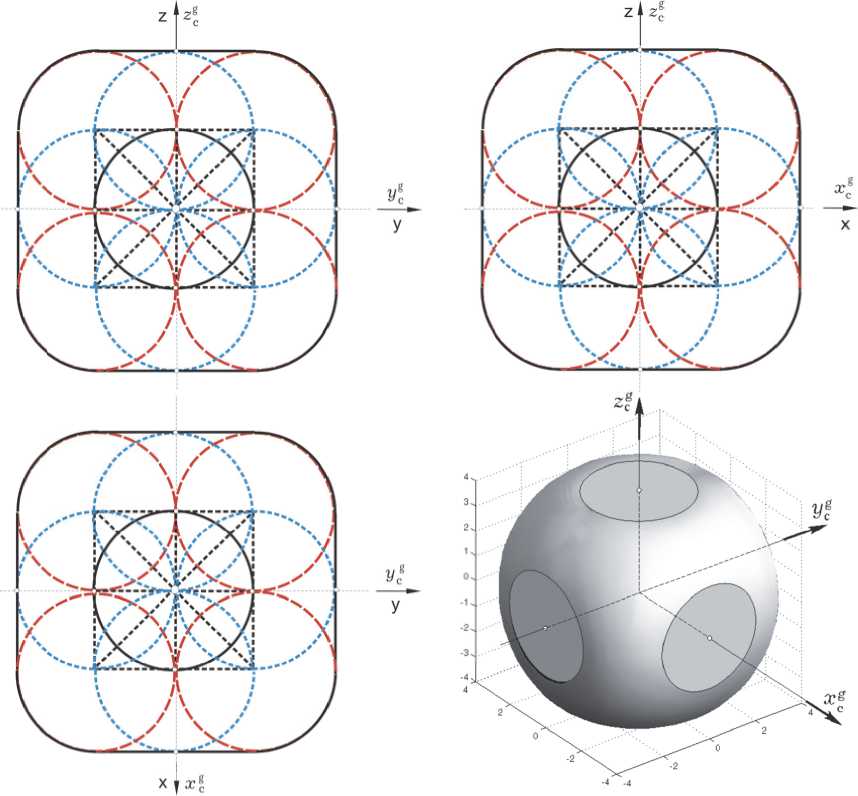
Рис. 5. Множества сингулярных состояний и оболочка области вариации КМ СГК

с помощью МП при переводе его углового положения из произвольного, достигнутого при завершении режима успокоения, в такое угловое положение, при котором орт n p нормали к плоскости панелей СБ направлен на Солнце; (iii) применении авторского метода разгона роторов ГД и приведения СГК в парковое состояние, при котором обеспечивается значение Н = 0 его вектора КМ; (iv) анализе процессов при включении СГК в СУО, автономном угловом наведении и управлении КА с приведением его ориентации к заданной в ОСК и последующей угловой стабилизацией.

АВТОНОМНОЕ УГЛОВОЕ НАВЕДЕНИЕ

Если считать, что СУО при отсутствии внешних возмущений и неподвижных панелях СБ со значением Y p = Y = 0 является сбалансированной по вектору суммарного КМ ( G = J to+ Н = 0 ), то пространственное угловое движение КА описывается уравнениями

Л = Л°ю/2; ю = J-Mg = е = и. (5)

Пусть для формирования вектора управляющего углового ускорения u ≡ ε применяются измерения кватерниона Л ( t ) , которые используются для вычисления вектора МПР а ( t ) , и вектора угловой скорости ю ( t ) . Тогда модель (5) представляется в непрерывной векторной форме

= |(1 - о ²) ю + 2 а х ю +1 ( а , ю ) ст ; ю = u (6) с заданными начальными условиями О ( t _о) = О _о , О ( t _о) = Ю _О при t ₀ = 0 , где при обозначении e ₀ = e ( t _о ) вектор ю ( t ) = { to i ( t )} является произвольным с условием | Ф _о | < 2 п . Будем считать, что вектор u = {u i } ограничен по модулю | u ( t )| = u ( t ) <  u^m , u^m >  о , а вектор ю ( t ) = { ю i ( t } ограничен по модулю | ю ( t )| = ю ( t ) <ю ^т , ю ^т >  0 , естественно Ю о = I Ю о 1 ^О ^т.

Для эталонной модели автономного наведения (6) в нашей статье [1] решена задача формирования нелинейного цифрового управления uk = u(CTk, юk ) (7)

в моменты времени tk с периодом дискретности Tu и ограниченными модулями век- торов управления и угловой скорости. В этой статье замкнутая модель автономного наведения (6), (7) применялась при переходе КА из произвольной ориентации, достигнутой при завершении режима успокоения КА, в орбитальную ориентацию. При этом ориентация ОСК Ox0 У ° z0 в ИСК определялась матрицей Co и кватернионом Л0, а угловое положение ССК в ОСК представлялось углами крена Ф1 , рыскания ф2 и тангажа ф3 в последовательности 312, кватернионом ошибки ориентации Е = (е0, е) = Л0 ° Л с вектором ё = {ei}, которому соответствуют вектор параметров Эйлера E = {е0,ё}, матрица ошибки ориентации ^ё

C ^e ( E ) = 1 3 - 2[ ё x ] Q e где Q _е = 1 3 ^ё 0 + [ ^ё ^ ] , вектор МПР О ^е = е /(1 + е ₀) = е tg( Ф ^е/4) и вектор-столбец погрешности ориентации 5 ф = {5ф i } = { 2 ^ё ₀ ^ё } . Вектор погрешности угловой скорости вычисляется по соотношению З го = го — С ^е го ⁰ , где го ⁰ является измеряемым вектором абсолютной угловой скорости ОСК. Применяемая здесь стратегия автономного углового наведения КА содержит два этапа: (i) угловое наведение КА при его переходе из произвольной ориентации в малую окрестность требуемого углового положения орбитального базиса в назначенное время, когда используется эталонная модель (6), (7) с учетом ограничений и дискретные измерения кватерниона ориентации Л ₀ и вектора го ₀ угловой скорости КА; (ii) автономное угловое наведение КА в малой окрестности перемещения орбитального базиса на основе требования для кватерниона невязки Е k = Л 0 ° Л k = 1 с единичным кватернионом 1 по измерениям кватернионов ориентации Л ⁰ и Л ₀ , а также векторов угловой скорости го 0 и ускорения £ к = ГО 0 ОСК в инерциальном базисе.

В данной статье описанная стратегия ав- тономного углового наведения применяется дважды: 1) при переходе КА от произвольной ориентации, достигнутой при завершении режима успокоения, к требуемой ориентации с наведением панелей СБ на Солнце; 2) после завершения разгона роторов гиродинов при переходе КА от ориентации на Солнце в орбитальную ориентацию.

РЕЖИМ УСПОКОЕНИЯ

Алгоритмы управления магнитным приводом в режиме успокоения КА детально представлены в статье [1]. Здесь применяется сочетание закона управления, оптимального по быстродействию на начальном этапе успокоения, с автоматическим переключением на локально-оп- тимальный закон управления с минимальным принуждением. При этом направление вектора механического момента магнитного привода M = Mт(го) определяется ортом k вектора КМ K = Jro корпуса КА. Пусть в момент времени t0 = 0 известен вектор го0 = го (t0) произвольного направления с модулем | го0 | = го0 < го0 при заданном значении го0. Тогда при тензоре инерции J корпуса КА в этот момент времени становится известным значение вектора КМ K(t0) = K0 = J го0 с модулем К0. Задача успокоения вращательного движения КА состоит в разработке закона управления M = M(ro), который начиная с момента времени t1 обеспечивает выполнение условия го( t) е S т = (го ( t ):| го( t) | t *), где скалярная константа А0го определяет размер множества Sm. Будем считать, что в моменты т времени tr = rT вектор индукции магнитного поля Земли B r = B(tr) = B rb r измеряется магнетометром. При формировании команды Mr =-a Kr для вектора механического момента МП на каждом полуинтервале времени t е [tr, tr+1) с заданным периодом T™ сначала определяется вектор потребной вариации импульса (pulse) управляющего момента

М p = t r ^{+ 1} М ( т ) d т = — a t r ^{+ 1} К ( т ) d т r          ^tr                                        ^tr

= — К _r (1 — ехр( — aT ,^m)) k _r .

Этот вектор представляется в виде M p = b r X ( M p X b r ) + b r ( M p , b r ) и для энергетической экономичности МП назначается вектор M p = M p ^m = b r x ( M p x b r ) с условием ( M p , b r ) = 0 .

Вектор потребной вариации импульса управляющего момента МП M p ^m = -A I m k r с модулем A I “ = К _r (1 — ехр( — aT™)) и ортом k r далее используется для формирования цифрового управления ЭММ L _r = { l ir } МП с периодом T™ . При этом определяется взаимная ориентация ортов b r и k r , если | ( b _r , k _r )| > cos( n /3) , то на текущем периоде дискретности МП не включается, иначе формируется вектор ЭММ L _r = ( A I ™ / T ^Xb _r X k _r )/ B _r с ограниченными компонентами | l_r | <  1 ™ .

Аналогичный алгоритм цифрового управления МП применяется для автоматической разгрузки кластера гиродинов от накопленного кинетического момента.

Режим успокоения (остановки вращения) КА начинается в момент времени 10 = 0 с вектором го0 произвольного направления при его модуле |гоо | = юо < юо и заканчивается в мо- мент времени to = t1* при произвольных значениях кватерниона Л ° и вектора угловой скорости О° е S ю с заданной константой А0.

НАВЕДЕНИЕ НА СОЛНЦЕ

В используемой концепции данного режима предусмотрено три этапа:

• 1)    перевод ориентации корпуса КА к требуемой в ИСК относительно орта s направления на Солнце, когда угол φ ^s _y = arccos 〈 b ₂ , s 〉 = 0 ;

• 2)    угловая стабилизация корпуса КА, накопление измерительной информации и перевод ориентации корпуса КА в такое усредненное за виток ССО угловое положение в ИСК, относительно которого устанавливаются устойчивые нелинейные угловые колебания КА, обусловленные влиянием внешних возмущающих моментов и управляющего момента магнитного привода;

• 3)    продолжение угловой стабилизации корпуса КА с помощью МП и разворот панелей СБ с помощью одноосного шагового привода относительно корпуса КА к такому положению, где будет достигаться минимальное усредненное за виток ССО угловое рассогласование ϕ _s ^p = arccos 〈 n ^p , s 〉 между ортом n ^p в РСК P и ортом ^s направления на Солнце.

Угловое положение орта s относительно плоскости земного экватора в течение года изменяется в диапазоне [-εe,εe] . Для наглядного представления детальной информации о положении орта np относительно орта s вводится подвижная солнечно-эклиптическая система координат O ⊕ xes yes zes с началом в центре Земли O⊕ , где ось O⊕ xes направлена по орту s, ось O⊕ zes совпадает по направлению с осью OsZsI инерциальной солнечно-эклиптической СК Is , а ось O⊕yes дополняет систему до правой ортогональной. Положение орта np относительно орта s в такой СК определяется углом αp2 наклона орта np к плоскости земного экватора (аналог широты) и углом α1p отклонения про-p екции орта n на плоскость земного экватора от оси XIe ИСК I⊕ (аналог долготы). Для любой ССО высотой до 1000 км угловое рассогласование между направлениями из центра Земли O⊕ и из центра масс O спутника на центр Солнца O s не превышает 10 угл. сек. Такое рассогласование в дальнейшем не учитывается.

В парковом положении панелей СБ направления осей РСК и ССК совпадают, при этом орт np =p2 =b2. На основе значений орта s направления на Солнце и орта no нормали к плоскости орбиты в ИСК I⊕ на борту КА определяется орбитальная солнечная система координат (ОССК) S с ортами s1,s2 и s3, которые формируются по соотношениям s2 =s; s3 =(s×no)/|s×no | ; s1 =s2 ×s3. (8) Для вычисления требуемого углового положения ССК B с ортами bi в ИСК I⊕ формируется матрица С = С8 = {[si ]} в виде столбца, составленного из строк [si ] ≡ sit . Целевой кватернион Л8 = (X0,X8) ориентации ССК в ИСК I⊕ определяется по матрице ориентации С8 = {[cij ]} , i, j e 1 ^ 3 на основе явных соотношений

X 0 = (1 + tr C ⁸)^1/2/2;

X 8 = ( C +u+ 2 — c i + 2 i + i )/(4 X 0 ) ;         (9)

i = 1 ^ 3, i + 3 = i .

Для исключения неопределенности типа (0/0) в процессе вычисления λ _i ^s , i = 1 ÷ 3 с помощью соотношений (9) при значении λ ^s ₀ = 0 используется известный алгоритм С. Стенли. Кватернион Е ⁸ = Л ⁸ ° Л = ( е ₀ ⁸ , е ⁸ ) и вектор МПР G ^e8 = { g ^е8} = tg( Ф ^е8 / 4) е ⁸ полностью определяют погрешность ориентации ССК B относительно ОССК S .

На первом этапе выполняется переориентация КА из произвольного углового положения при ti = to = t1* к требуемому положению ССК в ИСК I⊕ , которое определяется целевым кватернионом Л8. Здесь применяется эталонная модель автономного углового наведения [1] и управление ориентацией КА выполняется магнитным приводом, при этом на каждом витке орбитального движения КА, начиная с момента времени ti, определяется среднее значение е 8m                               -т- s eо скалярной части e0 кватерниона углового рассогласования Е8. Длительность этого этапа определяется моментом времени tii, когда удовлетворяется условие е™ ^ 0.9. При рациональном назначении параметра lm МП переходный процесс при любом значении угла фР(t.) = ф е8(t.) < п гарантированно завершается в момент времени начала витка с номером n = 4 . Здесь и далее отсчет номеров n витков ССО выполняется от момента времени очередного прохождения восходящего узла. В результате устанавливаются устойчивые нелинейные угловые колебания КА в окрестности «усредненного» положения орта b2 = np ССК. Разгон роторов в парах ГД начинается в этот же момент времени tii.

На втором этапе, по-прежнему при парковом положении панелей СБ (np = b2 ), начиная с момента времени tii на каждом n ≥ 4 витке ССО в моменты времени tr по значениям ортов b2 (tr) в ИСК I⊕ накапливается сумма Ξ b= Σb2(tr) , вычисляются ее модуль Ξ b=|| Ξ b || и усредненное за виток ССО зна- bm bb m

_{2 n} =Ξ / Ξ . Значение орта b _{2 n} подставляется вместо орта s в соотношения (8) и (9) для формирования очередного значения целевого кватерниона Л = ( X 0 ^m ₊₁Д ^J для следующего витка ССО с номером n + 1 .

Третий этап начинается в момент t = tiii ≥ tii , здесь на каждом n ≥ 4 витке ССО выполняется разворот панелей СБ на угол γ = γsp относительно оси Oz ССК. Этот угол определяет положение орта p2 = np нормали к плоскости панелей СБ, который в ССК представляется в виде столбца pb2(γ) = {-Sγ,Cγ.0} . В момент времени t = tiii известно усредненное на предыдущем витке значение орта b2mn в ИСК I⊕ , который в ССК B имеет представление bmb mb mb mb T m

2 n ^{— { b} 2 nx ’ b 2 ny ’ b 2 nz ^} = ^{Л (} t iii ⁾ ° ^b 2 n ° ^{Л (} t iii ^{) .}

Оптимальное значение угла γ = γps определяется из условия f (Y) —

Нетрудно сообразить, что в общем случае ось O z и орт b ₃ ССК не ортогональны плоскости, которая содержит усредненное на предыдущем витке ССО значение орта b ₂ ^m _n , соответствующее направлению на Солнце. Поэтому такой разворот панелей СБ может лишь свести к минимуму усредненное угловое рассогласование ϕ _s ^p = arccos 〈 n ^p , s 〉 между ортом n ^p к плоскости панелей СБ и ортом s направления на Солнце.

На витках ССО с номерами n ≥ 4 на борту КА рассчитываются очередные значения целевого кватерниона Л ^sm и потребного угла поворота γ ^p панелей СБ, однако их фактический разворот можно выполнять не на каждом витке [3], так как положение орта s относительно плоскости земного экватора изменяется со средней угловой скоростью ≈ 3.91 град/месяц.

РАЗГОН РОТОРОВ И ПРИВЕДЕНИЕ СГК В ПАРКОВОЕ СОСТОЯНИЕ

Для СГК по схеме 3-SPE в плоскости изменения КМ каждой i -ой паре ГД введем линии b_i , ортогональные линиям a_i , рис. 6 a , и будем считать, что направления осей роторов нечетных ( p = 1,3,5) и четных ( p = 2,4,6) ГД в парах i = 1 ÷ 3 зафиксированы в корпусе КА с помощью арретиров по линиям b_i при углах ГД относительно осей их подвеса β _{2 i - 1} = β _{2 i} - π , так как согласно применяемой стратегии отсчета углов гиродинов нечетные ГД в парах всегда перемещаются впереди четных, см. рис. 1 и рис. 6 a .

При последовательном разгоне двух гиророторов в каждой паре ГД с одинаковыми ускорениями в противоположных направлениях вплоть до номинального значения h _g их собственных КМ инерционные возмущающие моменты компенсируются. В результате КМ роторов всех шести ГД принимают значения h _g без влияния их инерционных возмущающих моментов на угловое движение корпуса КА и при отключении арретиров гиродинов СГК готов для приведения его в парковое состояние.

При развороте двух ГД c противоположными векторами КМ в i -ой паре в разные стороны с одинаковыми скоростями относительно осей подвеса создаваемые ими гироскопические моменты складываются, а вектор КМ h _i ( t ) этой пары ГД изменяется вдоль центральной линии a_i , см. рис. 6 b . Поэтому приведение СГК в парковое состояние с условиями Н ( t ) — 0 и М ^g (t ) = — Н * ( t ) — О рационально выполнять указанные развороты ги-родинов во всех трех парах одновременно в следующей последовательности:

• 1)    все шесть ГД разворачиваются в соответствующих направлениях с одинаковыми постоянными угловыми скоростями до значений их углов β ˆ _{2 i - 1} = β ^* _{2 i - 1} -χ , β _{2 i} = β ^* _{2 i} +χ в парах i = 1 ÷ 3 с заданным постоянным углом χ , далее принимается χ = 1 град;

  

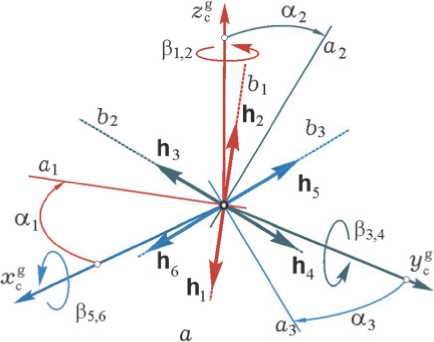
  Рис. 6. Схемы разгона роторов в парах гиродинов ( a ) и приведения СГК в парковое состояние ( b )

  
  
  
  
  

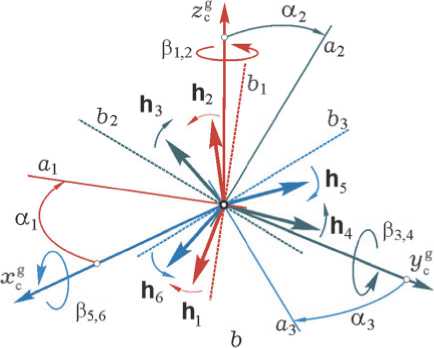
• 2)    задается потребный управляющий гироскопический момент СГК M ^g ≡ 0 и включается закон его настройки, который автоматически приводит СГК точно в парковое состояние.

В статьях [4,5] подробно представлены результаты исследования динамических процессов при разгоне роторов шести гиродинов и последующем приведении СГК в парковое состояние.

В момент времени t = t ₂ рассмариваемый режим заканчивается и СУО переходит в режим приведения ориентации КА к заданной в ОСК с последующей угловой стабилизацией.

ОРБИТАЛЬНАЯ ОРИЕНТАЦИЯ

По измеренным БИНС в момент времени t ₂ значениям векторов расположения r _o и скорости v _o поступательного движения центра масс КА (шесть координат состояния) на его борту по явным аналитическим соотношениям вычисляются сначала значения кватерниона Л ° ( 1 ₂) = Л ° , шести кеплеровых элементов орбиты и вектора угловой скорости ® ° ( 1 ₂) = to ° , а затем прогнозируемые значения постоянного кватерниона Л ° ( t«) = Л ° и вектора угловой скорости ю ° ( t , ) = to ° в инерциальном базисе I _е для момента времени e = 1 2 + T * , подробности представлены в [1].

Приведение углового положения КА к орбитальной ориентации выполняется в два этапа:

• 1)    в момент времени t ₂ ^* СГК включается в контур управления и ∀ t ∈ [ t ₂ ^* , t ₃ ^* ) требуемое изменение ориентации КА реализуется вектором управляющего момента СГК

М X = Ju k + to _k x G _k ,       (11)

где G k = Jto _k + H _k , с использованием дискретных значений вектора u _k эталонной модели автономного углового наведения [1] и распределением вектора M _k ^g между шестью ГД с учетом ограниченности модулей | β _p ( t ) | ≤ β ^m , p = 1 ÷ 6 угловых скоростей вокруг осей подвеса ГД ; здесь t ₃ ^* >  t ₂ ^* является моментом времени, когда выполняется двойное условие

Φe(t3*)≤Φ*e& ω(t3*)≤Δoω с заданным малым углом Φ *e вектора МПР Ge = e/(l + ё0) = e tg^ e/4);

• 2)    в момент времени t = t ₃ при малой погрешности углового положения базиса B относительно базиса O работа эталонной модели автономного углового наведения прекращается и начинается фильтрация значений вектора углового рассогласования £ _l = -5ф _l = - 2 е _{0 l} е _l , l е N ₀ с формированием векторов £ f , k е N ₀ ,

которые используются в законе управления СГК gk+i = Bgk + C £ k;     ink = К (gk + P £ 1); (12)

Mg f f e о e о         ~ k =® k x G k + J(C k £ к + LC kto К XJ®k + m k )

с периодом Tu , где Gfk = Jωfk + Hfk и при обозначениях du = 2/Tu ,a = (duTi-1)/(duTi+1)

элементы диагональных матриц B , P и C вычисляются в виде b = (duT2 -1) /(duT2 +1); p = (1 - b)/(1 - a);

c ≡ p ( b - a ) с настраиваемыми параметрами τ₁ , τ₂ , а также k в диагональной матрицы K .

КОМПТЬЮТЕРНАЯ ИМИТАЦИЯ

Рассматривался КА массой 1000 кг, который выведен на ССО высотой 720 км и долготой восходящего узла 30 град, при раскрытых панелях СБ его тензор инерции J = diag{812, 587, 910} кг м².

Будем считать, что применяемый магнитный привод имеет ограничение 1^m=150 Am² для компонентов вектора ЭММ и период цифрового управления T_u ^m = 4 с, причем МП работает во всех режимах начальной ориентации КА, в том числе при его орбитальном полете в тени Земли; номинальное значение собственного кинетического момента каждого из шести ГД h _g = 10 Нмс, ограничение скорости его поворота р ^m = 10 град/c, а период цифрового управления ГД T _u = 0.25 с.

На рис. 7 представлена угловая скорость КА на всем интервале компьютерной имитации, где цветами выделены компоненты вектора угловой скорости – синим по крену, зеленым по рысканию и красным по тангажу, а черным цветом отмечены изменения модуля этого вектора.

При модуле | ω ₀ | = ω ₀ = 3 град/с вектора начальной угловой скорости режим успокоения КА выполняется на интервале времени t ∈ [0, t ₁ ^* ) , где момент времени t ₁ ^* = 13248 с, когда начинается переход СУО в режим ориентации на Солнце. Соответствующие изменения электромагнитного и механического моментов магнитного привода, а также вектора угловой скорости КА, представлены на рис. 8 и 9.

Режим приведения ориентации панелей СБ космического аппарата на Солнце и последущей длительной стабилизации такого положения КА с разгоном роторов гиродинов и приведением СГК в парковое состояние выполняется на интервале времени t ∈ [ t ₁ ^* , t ₂ ^* ) с, где момент времени t ₂ ^* = 47616 с, когда начинается переход СУО в режим орбитальной ориентации КА. Соответствующие изменения угла φ ^s _y отклонения орта b ₂ от направления на Солнце и угла γ ^p пе-

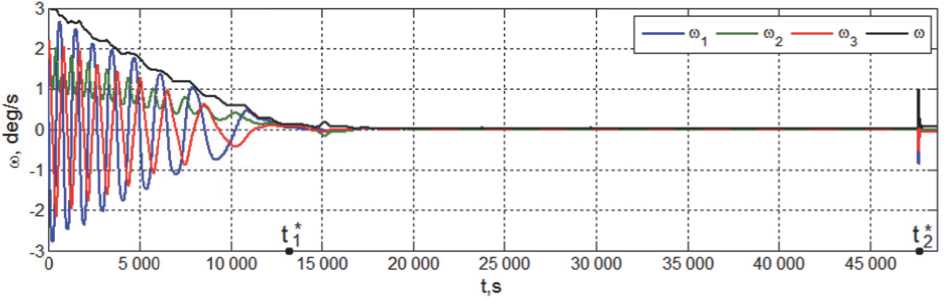
Рис. 7. Угловая скорость КА на всем интервале компьютерной имитации

О 2000     4000     6000     8000     10000    12000    14000    16000    18000

t,s

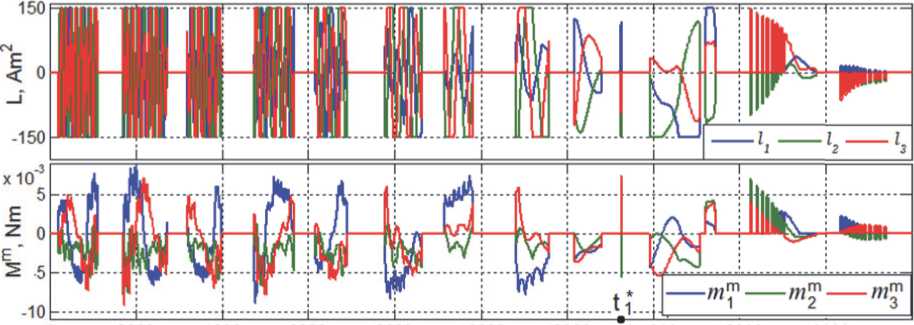
Рис. 8. Электромагнитный и механический моменты магнитного привода при успокоении КА и переходе СУО в режим ориентации на Солнце

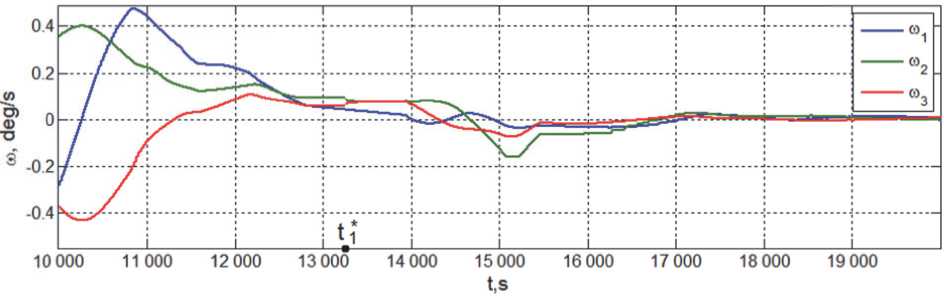
Рис. 9. Угловая скорость при завершении успокоении КА и переходе СУО в режим ориентации на Солнце

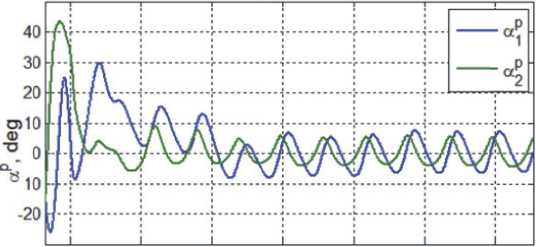
ремещения панелей СБ, а также углов α ₁ ^p и α ₂ ^p ориентации орта n ^p относительно направления на Солнце, представлены на рис. 10 и 11. Картина такой ориентации орта n ^p на интервале времени t ∈ [19000, 47616) с приведена на рис. 12, где красным цветом выделен символ Солнца.

Режим включения СГК в контур управления и приведения КА в орбитальную ориентацию с последующей угловой стабилизацией космического аппарата в ОСК выполняется на интервале времени t ∈ [47616, 48616) с. При этом на начальном интервала времени

**

t ∈ [ t ₂ , t ₃ ) , где

t ₂ ^* = 47616 с и t ₃ ^* = 47724.5 с, используется закон автономного углового наведения с ограничениями ω ^m = 1 град/с, u ^m = 0.15 град/с² и закон управления (11), а ∀ t ≥ t ₃ ^* применяется закон управления (12).

Рис. 13 и 14 представляют общую картину изменения угловых скоростей и углов ориентации КА при его переходе в орбитальную систему координат. Изменения цифровых команд управления гиродинами на начальном и завершающем

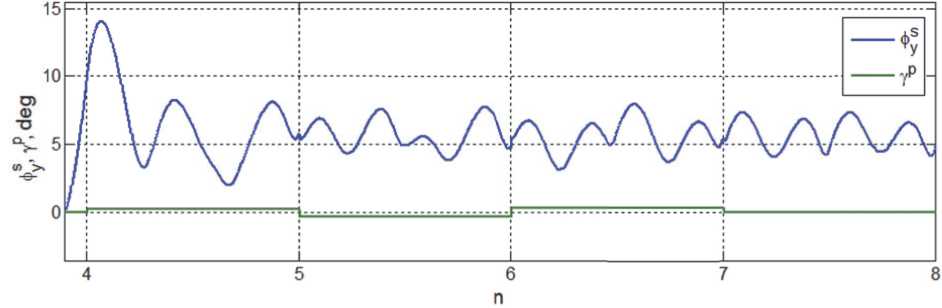
Рис. 10. Угол φ ^s _y отклонения орта b ₂ от направления на Солнце и угол γ ^p перемещения панелей СБ

15 000 20 000 25 000 30 000 35 000 40 000 45 000 t s

Рис. 11. Изменения углов ориентации орта n ^p в ССК

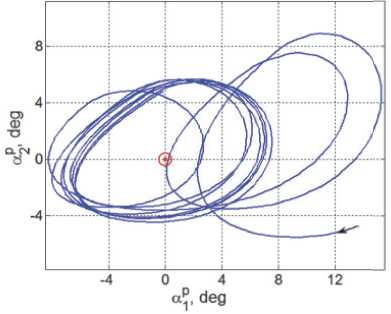
Рис. 12. О риентации орта n ^p в ССК

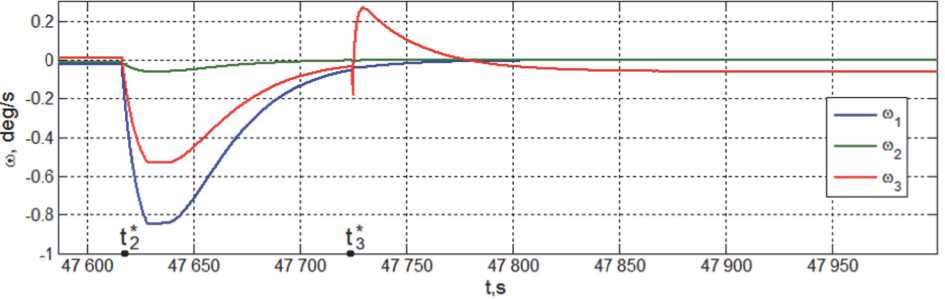
Рис. 13. Угловые скорости КА при переходе в орбитальную ориентацию

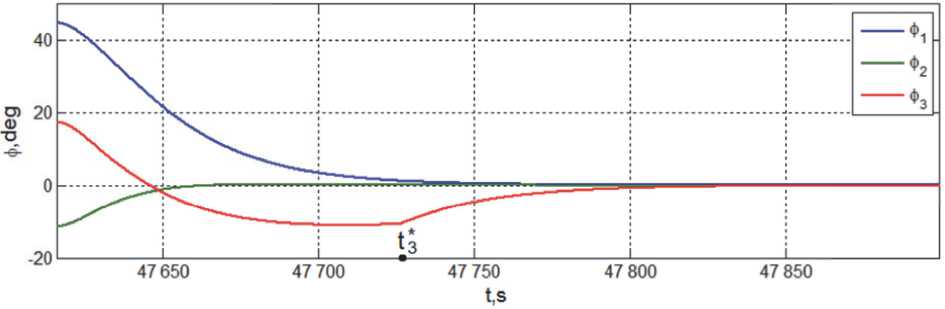
Рис. 14. Углы ориентации КА относительно орбитальной системы координат

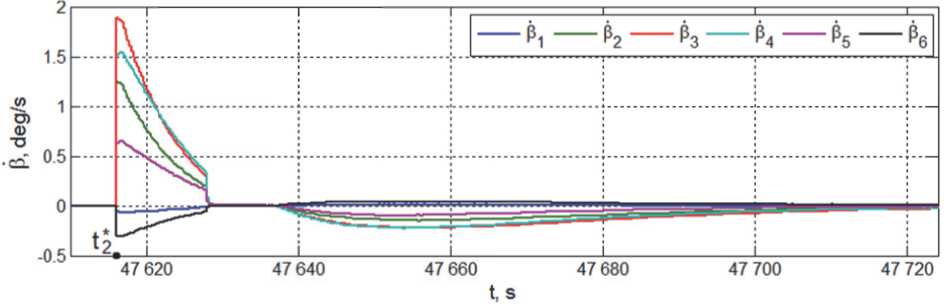
Рис. 15. Угловые скорости гиродинов при начале перехода КА в орбитальную ориентацию

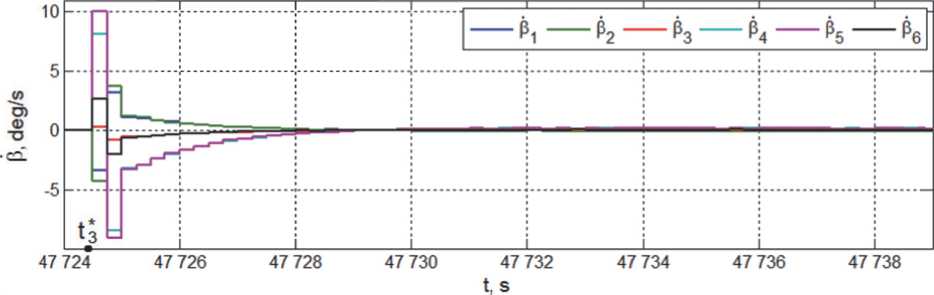
Рис. 16. Угловые скорости гиродинов при завершении перехода КА в орбитальную ориентацию

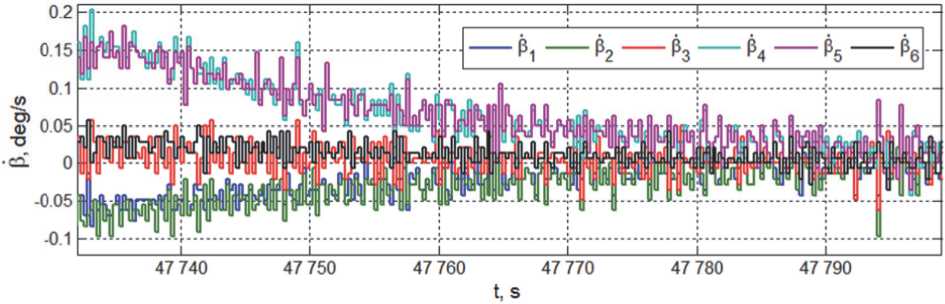
Рис. 17. Угловые скорости гиродинов при стабилизации КА в орбитальной ориентации

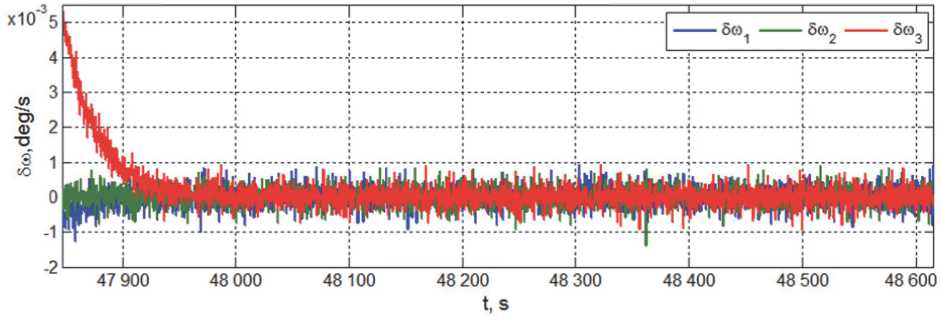
Рис. 18. Погрешности угловых скоростей КА при стабилизации в орбитальной ориентации

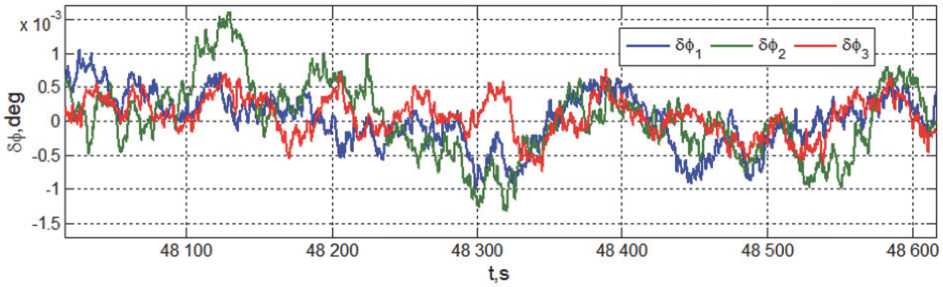
Рис. 19. Погрешности угловой стабилизации КА в орбитальной ориентации

этапах этого режима представлены на рис. 15 и 16, соответственно, а также на рис. 17. Наконец, погрешности установившейся стабилизации КА в орбитальной ориентации по угловым скоростям и углам приведены на рис. 18 и 19.

ЗАКЛЮЧЕНИЕ

Разработана новая стратегия начальной ориентации космического аппарата, оснащенного кластером шести гиродинов, после отделения его от ракеты-носителя с режимами успокоения, ориентации на Солнце, разгона роторов гиродинов и приведения кластера в парковое состояние, включения силового гироскопического кластера в контур цифрового управления космическим аппаратом и приведения его ориентации к заданной в орбитальной системе координат. Представлены численные результаты, демонстрирующие эффективность разработанных алгоритмов, которые могут применяться для информационных спутников и космических роботов.