Цифровой анализ прочностных характеристик радиальных рабочих колес энергетических турбомашин для АПК с учетом упругости вала

Репецкий Олег Владимирович, Хоанг Динь Кыонг; Repetckii O.V., Hoang Dinh Cuong

Научные статьи \ Математика. Естественные науки \ Математика \ Вычислительная математика. Численный анализ

Цифровой анализ прочностных характеристик радиальных рабочих колес энергетических турбомашин для АПК с учетом упругости вала

Автор: Репецкий Олег Владимирович, Хоанг Динь Кыонг

Журнал: Агротехника и энергообеспечение @agrotech-orel

Рубрика: Физическое, математическое, компьютерное и электромоделирование

Статья в выпуске: 4 (33), 2021 года.

Бесплатный доступ

Радиальные рабочие колеса турбомашин - это сложные вращающиеся детали. Вычислительные модели вала с радиальным рабочим колесом и 10-ю лопатками были построены с использованием параметрических моделей уменьшенного порядка. Цифровые модели учитывают влияние различных вариантов для жестких закреплений по кольцу вала и скорость вращения для исследования изменения собственных частот и напряжений турбомашин. В дальнейшем можно с уверенностью предположить, что исследование изменения собственных частот и напряжения турбомашин от скорости вращения и различных вариантов закрепления по кольцу вала являются актуальными на стадиях проектирования и доводки. Эти расчеты позволяются существенно сократить объем дорогостоящих экспериментальных исследований, уменьшить сроки конструирования и значительно снизить требуемые компьютерные ресурсы при проектировании новых конструкций турбомашин для АПК.

Еще

Радиальная лопатка, метод конечных элементов, рабочее колесо, собственная частота, статическое напряжение, турбомашина, форма колебаний

Короткий адрес: https://sciup.org/147235500

IDR: 147235500 | УДК: 519.6:62-135:621.824:620.1.052.3

Digital analysis of strength characteristics of radial impellers of power turbomachine taking into account shaft elasticity

Turbomachine radial impellers are complex rotating machine details. Computational models of a shaft with a radial impeller and 10 blades have been constructed using parametric models of reduced order. The models take into account the effect of different options for rigid fastening along the shaft ring and rotation speed to study changes in eigenfrequency and static stress of turbomachines. In the future, it can be assumed with confidence that the study of changes in eigenfrequency and static stress of turbomachines on the rotation speed and different options for rigid fastening along the shaft ring are relevant at the design and refinement stages. These calculations make it possible to significantly reduce the amount of expensive experimental research and reduce the design time. And they also make it possible to significantly reduce the required computer resources when designing new turbomachines.

Еще

Текст научной статьи Цифровой анализ прочностных характеристик радиальных рабочих колес энергетических турбомашин для АПК с учетом упругости вала

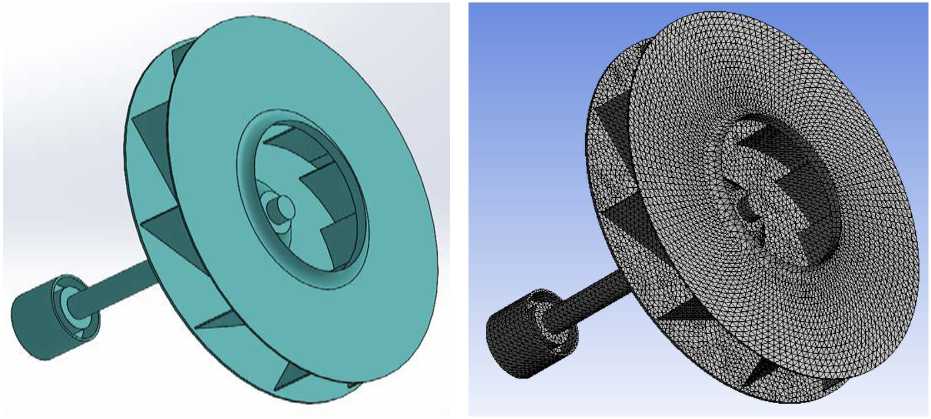
Введение. Для модели вала с радиальным рабочим колесом и 10-ю лопатками (Рис. 1) возникает большой динамический отклик. Собственные частоты резко увеличиваются в эксплуатационном диапазоне вращения. Также отмечается, что в конструкции возникает большая деформация вала. В этой связи, в конструкции модели нужно рассматривать различные варианты для жестких закреплений по кольцу вала. По этому критерию, конструкция модели вала с радиальным рабочим колесом с 10-ю лопатками имела два варианта закрепления по диаметру вала в соответствующих узловых точках конечных элементов [1]. Первый вариант предусматривал что, в кольце 1 применялось жесткое закрепление, а в кольце 2 сохранена свобода перемещений в осевом направлении и оставлено закрепление в остальных осях. А второй вариант – в кольце 1 и 2 применялось жесткое закрепление [2]. Полученные результаты позволяют значительно снизить требуемые компьютерные ресурсы при проектировании новых турбомашин в АПК.

Материалы и методы исследования

Расчеты на прочность и компьютерное моделирование модели радиального рабочего колеса с валом и 10-ю лопатками энергетических турбомашин показана на Pис. 1. Основные механические характеристики имеют вид: материал рабочего колеса – сталь, модуль Юнга – 2,1.105 Мпа, плотность – 7850 кг/м3, коэффициент Пуассона – 0.3. Общий вид модели вала с радиальным рабочим колесом представлен на рисунке 1а. В качестве конечноэлементной модели применяется конечный элемент ТЕТ10 комплексной программы ANSYS

WORKBENCH с общим количеством конечных элементов – 72712 и

138379 узловыми

точками. Количество степеней свободы составляет - 415137 (Рис. 1б).

Рисунок 1 - Модель вала с радиальным рабочим колесом с 10-ю лопатками (а- общий вид; б - конечноэлементная модель)

Расчеты на прочность и компьютерное моделирование технических процессов являются актуальными на стадиях проектирования, доводки и эксплуатации. Метод конечных элементов (МКЭ) является актуальным методом, который обычно используется в технических областях в различных вычислительных программных комплексах, например коммерческих системах, таких как ANSYS WORKBENCH, SOLIDWORKS или инициативных пакетам программ, например BLADIS+ [2,3,4] для решения задач статики, колебаний и расчета ресурса различных технических систем. МКЭ имеет общий алгоритм, который позволяется быстро выполнить расчеты различных вариантов сложных конструкций [3,4,5].

Уравнения движения с использованием МКЭ для анализа прочностных характеристик имеют вид [6,7,8]:

( [ K e ] + [ K g ] + [ K r ] ) - ! » } = { F _o) + { F t } + { F g } • ⁽¹⁾

и для проблемы свободной вибрации:

[ M №M C 1 5 M K E ] + [ K G H K R № = 0 • ⁽²⁾

где { 5 } - вектор смещения, [ K_E ] и [ M ] - матрицы упругой жесткости и массы, соответственно, [ K G ] - матрица геометрической жесткости, зависящая от скорости вращения и температуры, [ K _R ] - дополнительная матрица жесткости (псевдомасс), возникающая в результате вращения, { F } • { F T } • { F G } - векторы, соответствующие силам создается вращением, температурой и давлением газа соответственно. [ C ] - матрица Кориолиса.

Результаты и обсуждение

Первый вариант представлен на Рис. 2. Конструкция модели вала с радиальным рабочим колесом с 10-ю лопатками была закреплена по диаметру вала в соответствующих узловых точках конечных элементов. В кольце 1 применялось жесткое закрепление, а в кольце 2 сохранена свобода перемещений в осевом направлении и оставлено закрепление в остальных осях.

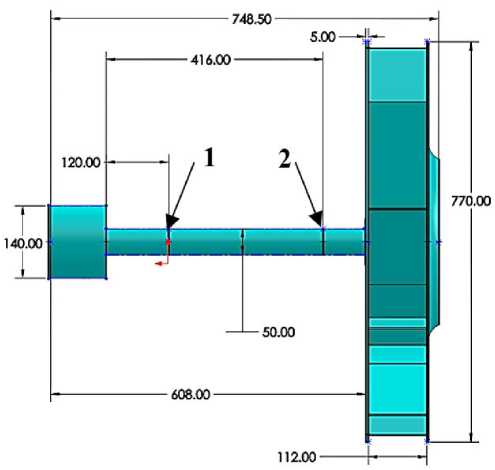
Рисунок 2 - Вид закрепления валы по ограниченным условиям

На Рис. 3 представлены шесть основных форм колебаний для модели вала с радиальным рабочим колесом. Каждая форма колебаний обладает характерной деформацией, по критерию количества узловых диаметров и числа узловых окружностей (n / m), определяющих форму 3 и 4 – 0/0, форму 1 – 1/0, форму 5 – 0/1,форму 18 – 1/1, форму 10 – 2/0.

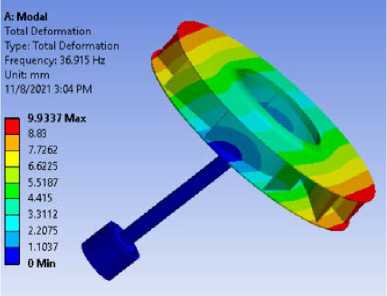
Форма 1

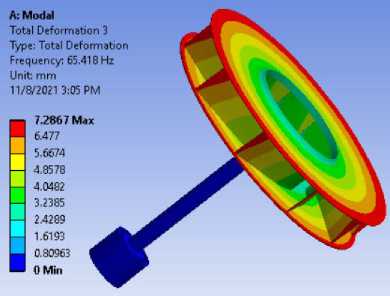
Форма 3

Форма 4

Форма 5

Таблица 1. Значения собственных частот колебаний для модели с учетом вала в комплексной программе ANSYS WORKBENCH.

Форма n / m	Эксперимент, Гц	Собственные частоты с учетом вала, Гц	Отклонение Δf, %	Максимальные значения деформаций, мм
0/0	-	65,418	-	7,2867
0/0	-	81,722	-	6,7255
1/0	44	36,915	16,1	9,9337
0/1	-	228,58	-	6,7904
1/1	-	438,7	-	15,756
2/0	341	341,6	0,17	19,06
5/0		402,36	-	33,694

Форма 10

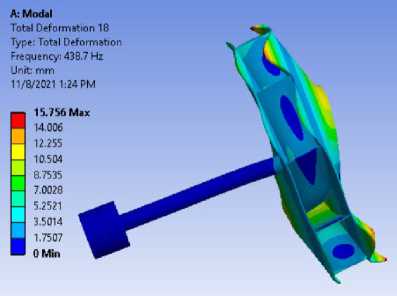
Форма 18

Рисунок 3 - Форма колебаний и собственные частоты модели с учетом вала с радиальным рабочим колесом 10-и лопаток энергетических турбомашин в программе ANSYS WORKBENCH.

Анализ таблицы 1 показал что, значения собственных частот колебаний от эксперимента для формы 1 отклоняется на величину около 16,1%, а для формы 10 на 0,17%.

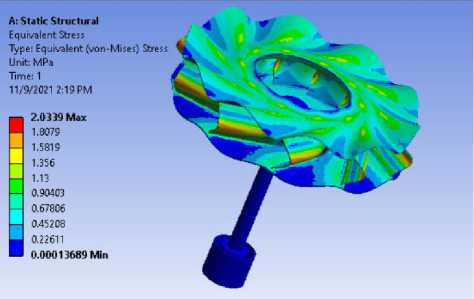
n = 5 (1/s)

Рисунок 4 - Расчеты статического напряжения с учетом вращения вала модели в комплексной программе ANSYS WORKBENCH.

Для анализа прочности и надежности радиальных рабочих колес от напряжений и

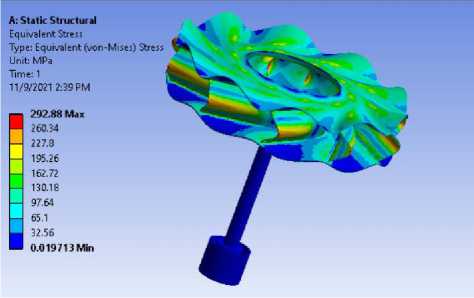
n = 60 (1/s)

собственных частот колебаний для этой модели с валом в проектировании компрессорного колеса, выполнены численные исследования статического напряженно-деформированного состояния (НДС) при оборотах 5 (1/s), 10 (1/s), 15 (1/s), 20 (1/s), 30 (1/s), 40 (1/s), 50 (1/s), 60 (1/s).

На Рис. 4 и в таблице 2 показываны расчеты статического напряжения σ э для этой модели с учетом вращения.

Таблица 2. Значение статического напряжения σ э для этой модели с учетом вращения, МПа

Скорость вращения колеса, 1/s	Эксперимент, Мпа	BLADIS+ (с валом), Мпа	Максимальные статические напряжения модели, Мпа
5	-	-	2,0339
10	-	-	8,1356
15	-	-	18,305
20	32	29,94	32,542
30	-	-	73,220
40	-	-	130,17
50	-	-	203,39
60	-	-	292,88

Расчеты значения собственных частот колебаний для этой модели с учетом вращения представлены в таблице 3.

Таблица 3. Расчеты значения собственных частот колебаний для этой модели с учетом вращения, Гц

Форма	Собственные частоты колебаний, Гц
Форма	0 (1/s)	5 (1/s)	10 (1/s)	15 (1/s)	20 (1/s)	30 (1/s)	40 (1/s)	50 (1/s)	60 (1/s)
1	36,915	37,162	37,887	39,061	40,641	44,809	49,969	55,76	61,901
2	36,924	37,168	37,893	39,068	40,648	44,815	49,975	55,766	61,906
3	65,418	65,432	65,444	65,462	65,487	65,551	65,625	65,702	65,777
4	81,722	81,789	81,99	82,324	82,79	84,112	85,935	88,229	90,959
5	228,58	228,58	228,6	228,62	228,66	228,77	228,92	229,1	229,33
6	228,62	228,61	228,63	228,66	228,7	228,81	228,96	229,14	229,37
7	289,09	288,7	288,59	288,4	288,13	287,37	286,29	284,91	283,21
8	289,38	288,97	288,85	288,66	288,4	287,63	286,56	285,18	283,48
9	339,82	339,98	340,45	341,23	342,31	345,38	349,62	354,98	361,38
10	341,6	341,79	342,39	343,39	344,79	348,71	354,06	360,74	368,63
11	341,64	341,84	342,44	343,44	344,84	348,76	354,12	360,8	368,69
12	402,36	402,77	404,11	406,34	409,43	418,13	429,99	444,73	461,04

Расчеты собственных частот колебаний для модели вала с радиальным рабочим колесом с 10-ю лопатками подобраны в таблице 4 по критерию числа узловых диаметров и узловых окружностей (n / m).

Таблица 4. Значения собственных частот колебаний для модели вала в комплексной программе ANSYS WORKBENCH по критерию числового узлового диаметра на числовой узловой окружности.

Форма n / m	Значения собственных частот колебаний в ANSYS WORKBENCH, Гц
Форма n / m	0 (1/s)	5 (1/s)	10 (1/s)	15 (1/s)	20 (1/s)	30 (1/s)	40 (1/s)	50 (1/s)	60 (1/s)
0/0	81,72	81,78	81,99	82,32	82,79	84,11	85,93	88,22	90,95
1/0	36,91	37,16	37,88	39,06	40,64	44,80	49,96	55,76	61,90
0/1	228,5	228,5	228,6	228,6	228,6	228,7	228,9	229,1	229,3
2/0	341,6	341,7	342,3	343,3	344,7	348,7	354,0	360,7	368,6
5/0	402,3	402,7	404,1	406,3	409,4	418,1	429,9	444,7	461,0

Диаграмма Кэмпбелла показана на рисунке 5, где горизонтальная ось представляет скорость вращения ротора и вертикальная ось обозначает собственную частоту колебаний. Кривые динамические частоты указывают взаимосвязь между собственными частотами и скоростями вращения для каждой формы колебания [9]. В диаграмме анализируется 5-ть значений форм колебаний 1, 4, 5, 10, 12.

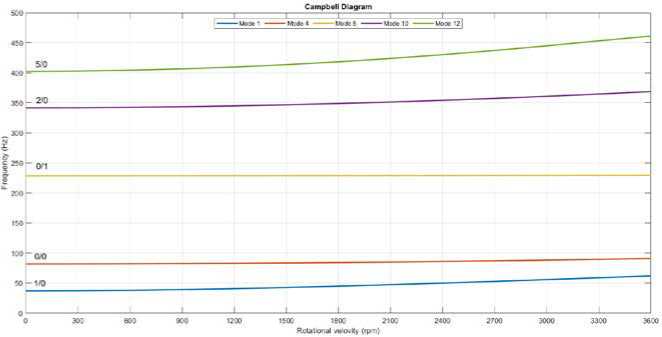
Рисунок 5 - Диаграмма Кэмпбелла для модели вала с радиальным рабочим колесом c 10-ю лопатками.

Второй вариант представлен на Рис. 2. Конструкция модели вала с радиальным рабочим колесом с 10-ю лопатками была закреплена по диаметру вала в соответствующих узловых точках конечных элементов. В зонах на кольцах 1 и 2 применялось жесткое закрепление.

На Рис. 7 представлены 6-ть основных форм колебаний для модели вала с радиальным рабочим колесом. Каждая форма обладает разнообразной характерной деформацией, по критерию количества узловых диаметров и числа узловых окружностей (n/m), определяющийся форму 4 – 0/0, форму 1 – 1/0, форму 7 – 0/1, форму 18 – 1/1, форму 10 – 2/0 и форму 12 – 5/0.

Таблица 5. Значения собственных частот колебаний для модели с учетом вала в комплексной программе ANSYS WORKBENCH.

Форма n / m	Эксперимент, Гц	Собственные частоты c учетом вала, Гц	Отклонение Δf, %	Максимальные значения деформацией, мм
0/0	-	81,991	-	6,7344
1/0	44	39,581	10,04	9,9429
0/1	-	319,62	-	8,3027
1/1	-	479,3	-	24,791
2/0	341	341,61	0,18	19,963
5/0	-	402,36	-	33,702

Таблица 6. Расчеты значения собственных частот колебаний для этой модели с учетом вращения, Гц

Форма	Собственные частоты колебаний, Гц
Форма	0 (1/s)	5 (1/s)	10 (1/s)	15 (1/s)	20 (1/s)	30 (1/s)	40 (1/s)	50 (1/s)	60 (1/s)
1	39,581	39,838	40,574	41,769	43,384	47,678	53,068	59,217	65,779
2	39,596	39,845	40,58	41,775	43,39	47,684	53,073	59,223	65,871
3	65,424	65,438	65,449	65,467	65,492	65,555	65,628	65,705	65,877
4	81,991	82,06	82,263	82,601	83,073	84,41	86,254	88,577	91,342
5	289,03	288,64	288,52	288,33	288,06	287,3	286,22	284,83	283,12
6	289,32	288,91	288,79	288,6	288,34	287,57	286,49	285,11	283,4
7	319,62	319,98	320,13	320,39	320,74	321,73	323,04	324,64	326,44
8	320,06	320,09	320,24	320,5	320,85	321,84	323,17	324,77	326,58
9	341,0	341,16	341,64	342,42	343,52	346,63	350,91	356,32	362,79
10	341,61	341,8	342,4	343,4	344,79	348,71	354,06	360,74	368,63
11	341,64	341,84	342,44	343,45	344,84	348,76	354,12	360,8	368,69
12	402,36	402,77	404,11	406,34	409,43	418,13	429,99	444,73	462,05

Таблица 7. Общие значения собственных частот колебаний для каждого варианта модели в комплексной программе ANSYS WORKBENCH и BLADIS+ [1].

n / m	Эксперимент, Гц	BLADIS+	Собственные частоты модели без учета вала, Гц	Собственные частоты модели с учетом вала (1й вариант), Гц	Собственные частоты модели с учетом вала (2-й вариант), Гц
0/0	_–	_–	80,263	65,418	_–
0/0	_–	_–	122,92	81,722	81,991
1/0	41	_–	41,513	36,915	39,581
1/0	_–	_–	47,963	_–	_–
0/1	_–	_–	356,11	228,58	319,62
1/1	_–	_–	365,33	_–	_–
1/1	_–	_–	425,99	438,7	479,3
2/0	341	349,0	341,62	341,6	341,61
5/0	_–	402,1	402,3	402,36	402,36

Вывод

Таким образом, в данной работе представлены основные формы колебаний и значения статических напряжений для модели вала радиального рабочего колеса c 10-ю лопатками энергетических турбомашин для перекачки воздуха в АПК. Также проводились экспериментальные исследования и сравнивались расчеты с данными эксперимента. Отмечается, что для двух вариантах модели с учетом вала собственные частоты уменьшаются по сравнению к моделью без учета вала для соотношения (n/m) и 0/0, 1/0, 0/1, 1/1. По каждому варианту наблюдаются уменьшение степени деформации вала в конструции и отсутствие значительного отклика собственных частот при вращении модели в диапазоне (45...50) 1/с. В этой связи можно предположить, что учет вала при численном анализе подобных конструкций не дает существенного эффекта и им можно пренебречь. Представленные кривые динамических частот показывают взаимосвязь между собственными частотами и скоростями вращения для каждой формы колебания в диаграмме Кэмпбелла и могут быть использованы в отстройке от резонансных режимов реальных конструкций радиальных рабочих колес в АПК.

Список литературы Цифровой анализ прочностных характеристик радиальных рабочих колес энергетических турбомашин для АПК с учетом упругости вала

Irretier H., Repetskiy O. Analyse der Eigenschwingungen rotierender axialer und radialer Laufräder und Schaufelpakete von Turbomaschinen mittels Hyperelemente, Kondensation und der Methode zyklischer Symmetrie. Kassel: GH Kassel Universität, Institut für Mechanik, 121 S.
Yan Y. J., Cui P. L. and Hao H. N. Vibration mechanism of a mistuned bladed disk // Journal of Sound and Vibration. 2008. Vol. 317.P. 294-307.
Yang M. T. and Griffin J. H. A reduced-order model of mistuning using a subset of nominal system modes // J Eng Gas Turb Power. 2001. Vol. 123. P. 893-900.
Repetckii O., Ryzhikov I. and Nguyen T. Q. Dynamics analysis in the design of turbomachinery using sensitivity coefficients // Journal of Physics: Conference Series. 2018. 012096.
Repetckii O., Ryzhikov I. and Springer H. Numerical analysis of rotating flexible blade-disk-shaft systems // Proceedings of the ASME Turbo Expo. 1999.
Whitehead D.S. Effect of mistuning on the vibration of turbomachine blades induced by wakes // Journal of mechanical engineering science. 1966. №. 1. Р. 15-21.
Castanier M. P., Pierre C. Modeling and Analysis of Mistuned Bladed Disk Vibrations: Status and Engineering Directions // Journal of Propulsion and Powers. 2006. №. 2 (122). Р. 384-396.
Ewins D. J. Vibration characteristics of Bladed disc assemblies // Journal of Mechanical Engineering Science. 1973. №. 5 (12). Р. 165-186.
Campbell W. The protection of Steam Turbine Disk Wheels from Axial Vibrations // Trans. of the ASME 46. 1924. Р. 31-160.

Еще