Цифровые двойники в управлении

Цифровые двойники

С развитием цифрового моделирования появилась возможность создавать модели, отображающие поведение объекта моделирования в реальном масштабе времени.

Некоторые аппаратные средства заменяются их цифровой программной реализацией.

«Цифровой двойник» – это цифровая копия физического объекта или процесса, помогающая оптимизировать эффективность бизнеса. Концепция «цифрового двойника» является частью четвертой промышленной революции, которая призвана помочь предприятиям быстрее обнаруживать физические проблемы, точнее предсказывать их результаты и производить более качественные продукты.

Такая модель должна удовлетворять условиям:

• 1.    Моделирование процессов должно обеспечивать получение результатов в реальном масштабе времени.

• 2.    Моделирующее устройство должно иметь интерфейсные средства, аналогичные объекту моделирования (примером служат виртуальные коммутаторы).

Только при выполнении этих условий модель может рассматриваться как «цифровой двойник».

Если моделируемые процессы протекают в модели с более высокими скоростями, чем в моделируемом объекте, то цифровой двойник способен обеспечить прогнозирование поведения объекта с целью управления. Прогнозирование позволяет компенсировать запаздывания в цепях управления и повысить качество регулирования в системах с обратной связью.

Применяемый при создании цифровых двойников математический аппарат зависит от сложности объекта и степени формализуемости задачи.

Различают два вида моделей, применяемых при создании цифровых двойников. Это модели временных рядов и модели предметной области [1].

• 1.    Модели временных рядов обеспечивают поиск зависимостей будущих значений состояний объекта от истории изменения этих состояний и построение прогноза по этим зависимостям. Эти модели универсальны для различных предметных областей и не зависят от физической природы переменных данного ряда.

• 2.    Модели предметной области используют законы данной предметной области. В них используются математические, логические и вероятностные свойства, присущие конкретной предметной области.

Ниже приводится два примера использования цифровых двойников, основанных на указанных типах моделей.

Цифровая модель запаздывания видеотрафика

Чаще всего технологии потокового вещания используют адаптивную потоковую передачу данных, основанную на НТТР (англ. HAS). Потоковая передача видеотрафика является наиболее значимым сервисом при оказании операторами связи услуг Интернет-TV и YouTube [2; 3].

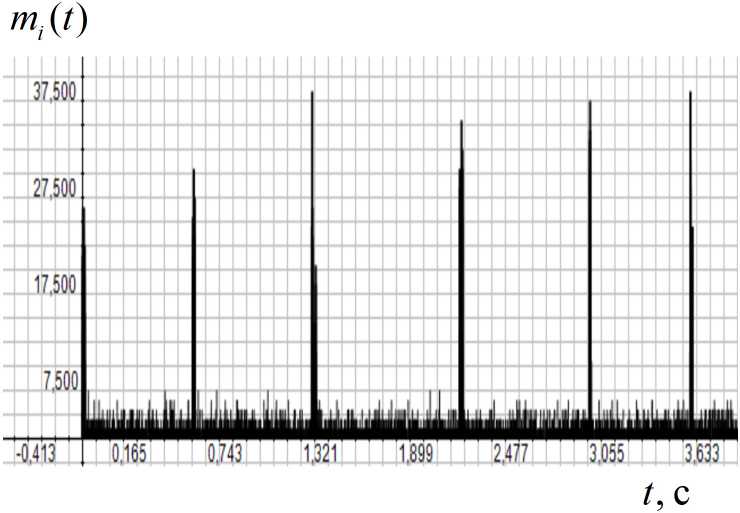
Рисунок 1 Суммарный трафик кодека Н264-10 000 и пуассоновского потока

В настоящее время HAS стал превалирующей формой интернет-трафика.

Имеется множество различных методов управления видеотрафиком. Как правило, все они основаны на буферизации принимаемого видеопотока перед его воспроизведением.

Принимаемые пакеты буферизируются в специальной буферной памяти, из которой непрерывно извлекаются и поступают на воспроизведение в реальном масштабе времени. Основная цель управления состоит в поддержании постоянным в буферной памяти некоторого объема пакетов, который бы обеспечил непрерывное воспроизведение в течение заданного интервала времени (например, в течение 10 с). Управление потоком на сетевом уровне и пользовательское качество восприятия (QoE) непосредственно связаны с буферным уровнем, который является центральным звеном управления ресурсами или возможной оптимизации [4; 5]. Если в процессе воспроизведения объем пакетов в буферной памяти достигнет своего нижнего предела, то возникают перерывы в воспроизведении, называемые «зависаниями».

Существует множество различных способов стабилизации объема пакетов, находящихся в очереди буферной памяти. В их числе следует отметить способ, использующий алгоритм «Кубик» [6]. В соответствии с алгоритмом, сервер увеличивает ступенчато, по кубическому закону, скорость передачи пакетов до тех пор, пока протокол TCP не покажет существенное возрастание ошибочно переданных пакетов. Обнаружив такое возрастание, сервер резко снижает интенсивность передачи, возвращаясь к исходному состоянию.

Недостатком подобного способа управления трафиком являются высокая инерционность и значительные потери пакетов при перегрузках. Ввиду его крайней неэффективности, современные способы основываются на измерении характеристик трафика не на передающей, а на приемной стороне [7]. В их числе, например, способ, основанный на применении алгоритма PANDA [8]. Указанные способы предусматривают передачу видеопакетов отдельными блоками (длительностью воспроизведения, например, 2 с). Между блоками имеются регулируемые временные интервалы (межблоковые интервалы). При уменьшении межблоковых интервалов происходит увеличение средней скорости передачи пакетов.

Предусматривается также возможность ступенчатого изменения скорости поступления информации от передающего кодека сервера в сеть (изменение битрейта).

В соответствии с алгоритмом, на каждом цикле передачи блока измеряется допустимая средняя скорость передачи, ступенчато устанавливается соответствующее значение битрейта и регулируется межблоковый интервал. Указанные регулировки имеют целью поддержания объема пакетов в буферной памяти приемника на заданном уровне.

В процессе управления видеотрафик запрашивается приемником и передается видеокодеком в виде отдельных сегментов, между которыми следуют паузы. Поэтому поток трафика носит явно выраженный пачечный характер и весьма значительно отличается от пуассоновского.

На рисунке 1 показаны суммарный трафик кодека Н264 -10 000 с коэффициентом загрузки р 1 = 0 , 1 и пуассоновского потока с интенсивностью X = 1000 пакетов в секунду при коэффици-

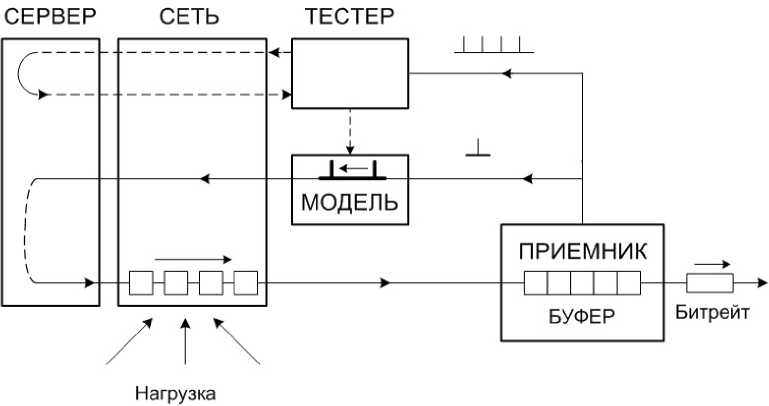
Рисунок 2. Введение прогноза в цепь обратной связи

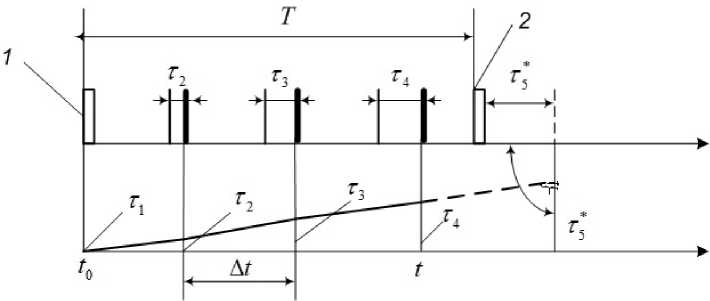
Рисунок 3. Прогнозирование задержки т *

енте загрузки р₂ = 0 , 8 . Потоки имеют одинаковые приоритеты обслуживания.

Ординаты графика показывают числа пакетов, поступающих в течение интервалов т , равных времени передачи пакетов в канале.

Пачечный трафик кодека Н264-10 000 хорошо заметен на фоне равномерного пуассоновского потока. Случайный характер изменения загрузки сети приводит к случайному процессу изменения задержек пакетов видеотрафика и необходимости управления размерами буфера на приемной стороне. Качество регулирования размеров буфера может быть повышено, если в системе управления постоянно учитывать указанные задержки и осуществлять их прогнозирование. Реализация процесса введения сигнала опережения поясняется на рисунке 2. Для определения задержек трафика в сети в нее периодически поступают тестирующие пакеты от тестера (в качестве тестирующих могут быть использованы сигналы запроса пакетов). Пакеты, пройдя по сети до сервера и возвратившись обратно, обеспечивают определение круговых задержек сети.

Получаемая информация обрабатывается, и в результате обработки формируется модель процесса запаздывания. На основании полученной модели производится прогнозирование запаздывания на расчетный момент подачи команды запроса очередного блока видеотрафика. Команда запроса подается с опережением (по отношению к расчетной) на величину спрогнозированного запаздывания.

На рисунке 3 показан процесс прогнозирования и учета задержки в сети. Команды запроса, поступающие циклично от приемника к передатчику, обозначены цифрами 1. Цифрой 2 обозначена команда, поданная в данном цикле с опережением во времени на величину т₅ . T обозначает время цикла без учета коррекции. В процессе функционирования приемник циклически посылает тестовые сигналы. Передатчик после получения сигнала, задержанного сетью, посылает приемнику ответный сигнал. Ответный сигнал также задерживается сетью и поступает в приемник. Таким образом, приемник определяет круговые задержки прохождения тестового сигнала по сети.

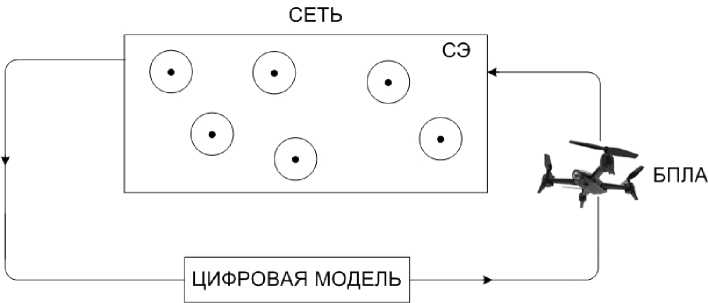
Рисунок 4. Замена аккумуляторов сенсорных элементов БСС с помощью БПЛА

Значения задержек в моменты опроса обозначены буквами т 1 , . ., т₅ . В соответствии с указанными задержками, формируется математическая модель, а на основании выбранной модели производится прогнозирование значения требуемой задержки очередной команды запроса трафика. На рисунке 3 на основании обработки результатов тестов т 1 , ^ , т₅ получается прогнозируемое значение времени задержки т * .

Очередной запрос 1 передается с опережением на время т * (обозначен цифрой 2), в результате чего происходит компенсация сетевых задержек и повышается качество процесса регулирования.

Если же требуемое время компенсации задержки т * окажется настолько большим, что запрос 2 должен поступить раньше, чем закончатся расчеты, то указанный запрос поступит непосредственно сразу же после завершения расчетов.

В качестве модели процесса изменения задержек в сети может быть выбраны вейвлеты или разностные интерполяционные формулы (например, формула Ньютона).

т * = т₀ + u А ⁽1 т₀ + u ⁽ u^ 1 ) А ⁽²⁾ т₀ + . .,

t = tn где и = - - число шагов, начиная от t до t, А t 0

А t - величина шага во времени, а А ⁽ i ) т₀ - разности i -го порядка. Практика показала, что вполне можно ограничиться разностями третьего порядка.

Подзарядка аккумуляторов беспроводных сенсорных сетей (БСС)

Другим примером является процесс управления беспилотным летательным аппаратом при зарядке аккумуляторов БСС. Техническое обслуживание и энергообеспечение элементов БСС представляют особые трудности для пространственно удаленных узлов сети. Эти элементы обычно питаются от автономных источников электроэнергии, нуждающихся в периодической подзарядке [8; 9].

Перспективной технологией подзарядки аккумуляторных батарей, позволяющей значительно увеличить срок службы элементов БСС, в настоящее время является способ подзарядки аккумуляторных батарей в сенсорных сетях при помощи беспилотных летательных аппаратов (БПЛА) [10].

Рассматриваемый в статье способ основан на концепции «цифровых двойников».

В качестве «цифрового двойника» здесь выступает показанная на рисунке 4 цифровая модель беспроводной сети.

Рассмотрим один из примеров алгоритма, реализующего этот способ. Имеется сеть сенсорных элементов СЭ с перезаряжаемыми аккумуляторными батареями. Аккумуляторы заменяются путем доставки и замены на стационарной станции сенсорных узлов c помощью БПЛА. Необходимо определить последовательность замены аккумуляторов с тем, чтобы в процессе замены ни один из аккумуляторов не успевал полностью разрядиться, при этом время, затраченное БПЛА в работе (коэффициент загрузки БПЛА), было бы минимальным.

На центральной базе всегда имеются готовые для замены СЭ с заряженными аккумуляторами. На центральной базе имеется поступающая по сети информация о степени зарядки аккумуляторов всех СЭ: Z ( I ; T ) – уровень заряда аккумулятора СЭ (устройства I ) в момент времени Т ; Z max( I ) – максимальный допустимый уровень заряда аккумулятора устройства I ; Z min( I ) – минимальный допустимый уровень заряда аккумулятора устройства I ; Т – время от начала полного цикла облета и зарядки всех СЭ БПЛА.

Известны координаты X ( I ), Y ( I ) – СЭ (устройств I ), а также координаты центральной базы X B и Y B. Следовательно, известны I L – расстояния от базы до сенсорного устройства I .

Z ( I ; 0) – уровень заряда аккумулятора сенсорного устройства I в момент начала цикла Т = 0.

Степень заряженности аккумулятора будем характеризовать временем, необходимым для его полной разрядки, начиная с момента Т :

TR ( T ; I ) = Z ⁽ I ^; T ) , VR max ( I ) где VR max ( I ) - максимальная скорость разряда аккумулятора устройства I .

Время, необходимое для прилета БПЛА от станции до сенсорного устройства I , определяется:

T ( D ; I ) = L ⁽ D ’ I ’ T ) ,

VD где L(D; I; T) – расстояние от БПЛА до сенсорного элемента I в момент времени Т, а VD – скорость полета БПЛА.

Время, необходимое для обслуживания БПЛА I-го сенсорного устройства, – TO ( D ; I ).

Время полного полета (с возвратом) БПЛА и обслуживания сенсорного устройства I

TPO ( D ; I ) = 2 T ( D ; I ) + TO ( D ; I ).

Перед началом полетов производится моделирование всего полного цикла обслуживания.

• 1.    Текущие значения Z ( I ; T ) располагаются в порядке их возрастания и выбирается элемент с минимальным значением Z ( I ; T ).

• 2.    Моделируется полное время TPO ( D ; I ) полета и обслуживания указанного элемента, а его степень заряженности на модели устанавливается максимальной Z max( I ).

• 3.    Моделируется процесс разрядки аккумуляторов всех остальных СЭ в течение времени TPO ( D ; I ). Затем происходит переход к пункту 1, и процесс повторяется до окончания моделирования подзарядки аккумуляторов всех СЭ.

После окончания цикла моделирования выбирается СЭ с минимальным уровнем остаточного заряда и определяется остаточное время, в течение которого данный СЭ способен работать (все остальные элементы имеют большие остаточные времена). Если из времени прохождения полного цикла вычесть остаточное время, то получим гарантированное допустимое время ожидания полета с начала процесса моделирования. В течение указанного времени БПЛА может находиться на базе. Указанное время ожидания является гарантированным нижним пределом, поскольку при моделировании использовались максимально допустимые скорости разрядки аккумуляторов. БПЛА не производит полет и продолжает ожидать. После окончания промежутка времени ожидания в модель вновь поступают из сети все необходимые данные о состоянии СЭ и цикл моделирования повторяется. Так происходит итерационное повторение циклов моделирования до тех пор, пока разность результатов, полученных между соседними циклами, достигнет установленного предела. После окончания моделирования становится известным номер СЭ, который требуется обслужить первоочередно, и такой элемент обслуживается БПЛА.

После окончания обслуживания указанного СЭ процесс моделирования повторяется сначала и циклически обслуживаются все СЭ.

Высокая скорость цифрового моделирования позволяет произвести оптимизацию последовательности обслуживания сенсорных элементов СЭ с ее привязкой ко времени, обеспечивая минимизацию полетного времени и безусловное отсутствие полной разрядки аккумулятора любого из сенсорных элементов. При этом модель взаимодействует с моделируемой сетью, постоянно получая от нее актуальную информацию о состоянии, что свойственно «цифровым двойникам».

Приведенный нами алгоритм подзарядки или замены элементов питания сенсорных узлов БСС с использованием БПЛА позволяет существенно увеличить время работы как элементов БСС, так и сети в целом.

Заключение

Цифровое моделирование является мощным средством изучения свойств действующих или проектируемых объектов. Если процессы в действующей модели протекают быстрее, чем в реальном объекте, то, снабдив модель интерфейсными средствами, с помощью которых моделируемый объект взаимодействует с внешней средой, мы получаем цифровое устройство со свойствами адекватными моделируемому объекту. Такая модель может быть встроена в реальную систему и называется цифровым двойником. Если быстродействие цифрового двойника выше, чем быстродействие моделируемого объекта, то появляется возможность прогнозирования протекающих в объекте процессов и использования результатов прогнозирования в системах автоматического управления этими процессами.