Цифровые фильтры как программные методы устранения помех в газоанализаторах

На газоаналитические приборы, применяемые на производстве, часто воздействует помеха промышленной электросети с частотой 50 Гц. Учитывая, что информационный сигнал от измерительной ячейки изменяется тоже в низкочастотном диапазоне 1..100 Гц, возникает существенная погрешность, для уменьшения которой применяют всевозможные аналоговые и цифровые фильтры. В настоящее время для борьбы с подобными помехами чаще используются цифровые фильтры, причем, в большинстве случаев при реализации последних можно обойтись и без специализированных сигнальных процессоров. Например, используя универсальный 8-битный микроконтроллер, уже имеющийся в составе газоаналитических приборов, поскольку его ресурсов бывает достаточно для обработки указанного низкочастотного сигнала.

В нашем случае для борьбы с помехами на частоте 50 Гц, был использован заграждающий фильтр 2 порядка, который рассчитывается методом размещения нулей и полюсов [1]. Фильтр осуществляет режекцию сигнала на частоте 50 Гц, а также имеет полосу среза по 5 Гц в каждую сторону, что показано на рисунке 1 [2]:

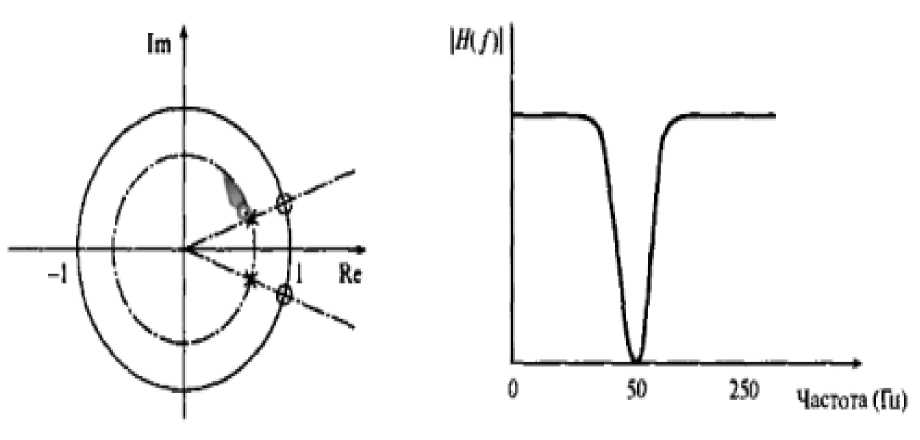
Рисунок 1 - Частотная характеристика и диаграмма нулей и полюсов заграждающего фильтра

Для подавления помехи с частотой 50 Гц пара комплексных нулей была помещена на окружности в точках с угловыми координатами:

φ1,2 = (Fзагр/Fдискр)*360º=(50/1000)* 360º = 18º(2)

Далее, с целью обеспечения полосы ослабления сигнала, полюса были помещены внутри самой окружности (на окружности с r<1). Учитывая ширину среза (Wполосы = 10), воспользовались формулой 3:

r ~ 1 - (Wполосы/Fдискр) * n = 0,9698(3)

Затем, исходя из диаграммы, была рассчитана передаточная функция:

(z-e-^j^z-e^1»0)

H(z) ==

1 — 1.9022 «z-1 + z-2

Схема заграждающего представлена на рисунке 2:

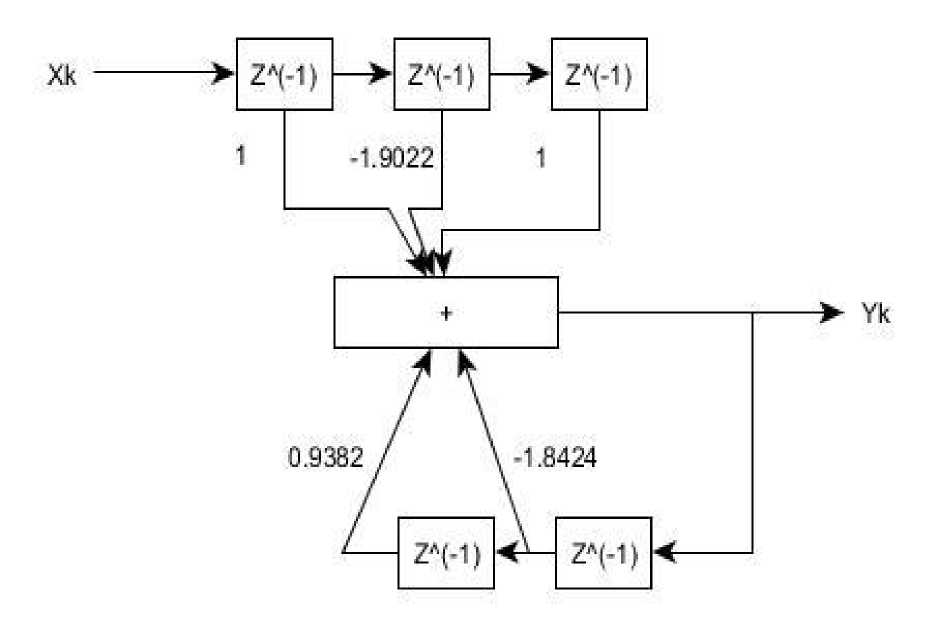
Рисунок 2 – Схема заграждающего фильтра

Полученная функция 4 была преобразована в разностное уравнение, которое было использовано при программировании:

y(n) = x n – 1,9022*x n-1 + x n-2 + 1,8424*y n-1 – 0,9382*y n-2      (5)

Расчёт фильтра Баттерворта 2 порядка был осуществлён методом билинейного z-преобразования. Для этого был определён нормированный аналоговый фильтр-прототип нижних частот 1 порядка с передаточной функцией:

H(S) = 1/(S+1)         (6)

Затем была проведена деформация критичных частот (0,05 и 100 Гц):

ω p1 ` = tg(ω p1 *T/2) = 0,00016

ω p2 ` = tg(ω p2 *T/2) = 0,3249             (7)

ω²= ω p1 ` * ω p2 ` = 0,000052

W = ω p2 ` - ω p1 ` = 0,32474

Порядок фильтра был удвоен из-за применения преобразования «фильтр нижних частот в полосовой фильтр» [3]:

s2 + coO2

s =                       (8)

Z - 1

Применив подстановку s =      [4] и соответствующие замены W и

2 ω0 было получено:

W *(z-i)*(z + 1)

H(z) =                                       =

0,2451 — 0,2451 »z"2

Схема полосового фильтра Баттерворта представлена на рисунке 3:

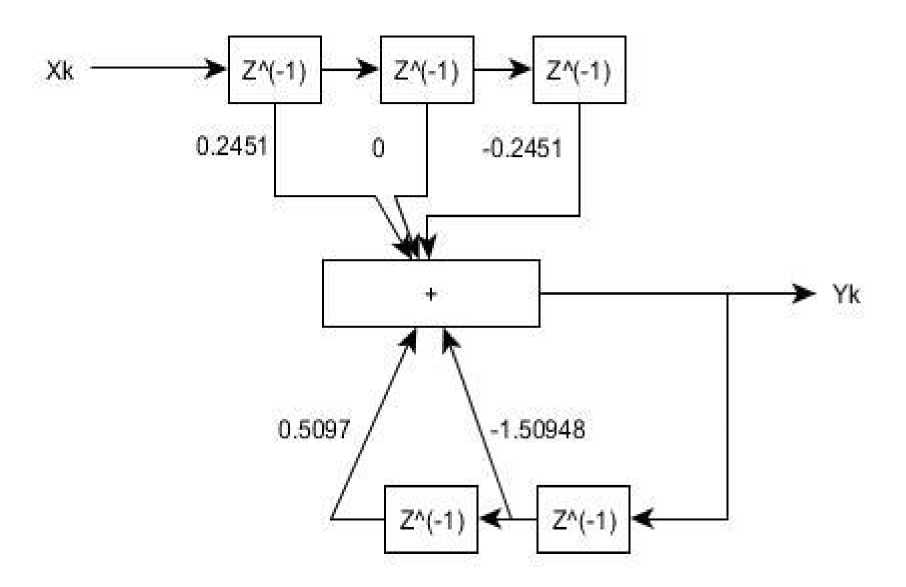
Рисунок 3 – Схема фильтра Баттерворта

Полученной передаточной функции 9 соответствует разностное уравнение:

y(n) = 0,2451*x n – 0,2451*x n-2 + 1,50948*y n-1 – 0,5097*y n-2   (10)

Для реализации фильтрации был описан массив значений дискретного входного сигнала (в данном случае с частотой Fдискр = 1000 Гц). Так же был введён массив передаточных функций (с помощью полученных уравнений), которые были рассчитаны выше и длины импульсной характеристики. После этого и была начата обработка исходного сигнала: обнулился массив входных значений, получили новые значения для этого массива, затем поэтапно вычислены значения выходного сигнала, записаны предыдущие значения входного сигнала и выводим значение выходного сигнала. Такая процедура описывает работу обоих фильтров. Схема алгоритма изображена на рисунке 4:

Рисунок 4 – Блок-схема алгоритма фильтрации

Для проверки полученных уравнений и алгоритмов проведено моделирование в системе Matlab, которая широко используется при построении математических моделей, а также позволяет обрабатывать большие массивы чисел, что актуально при фильтрации сигналов [5]. Был задан исходный сигнал (гармонический сигнал с частотой 100Гц), который был подвергнут зашумлению высокочастотными помехами, а так же помехой с частотой 50 Гц. После чего, полученный результат был подвергнут обработке рассчитанными выше фильтрами, результат работы которых можно пронаблюдать на рисунках 5 и 6, где приведены соответственно: исходный зашумлённый сигнал и сигнал, обработанный цифровыми фильтрами.

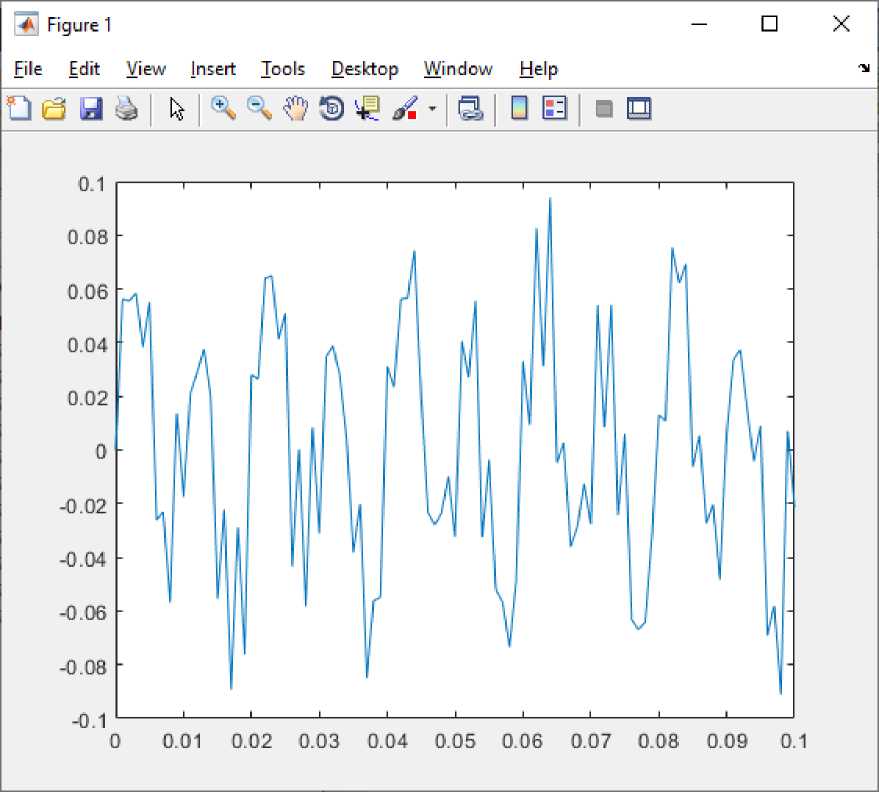
Рисунок 5 - Исходный сигнал (с шумом)

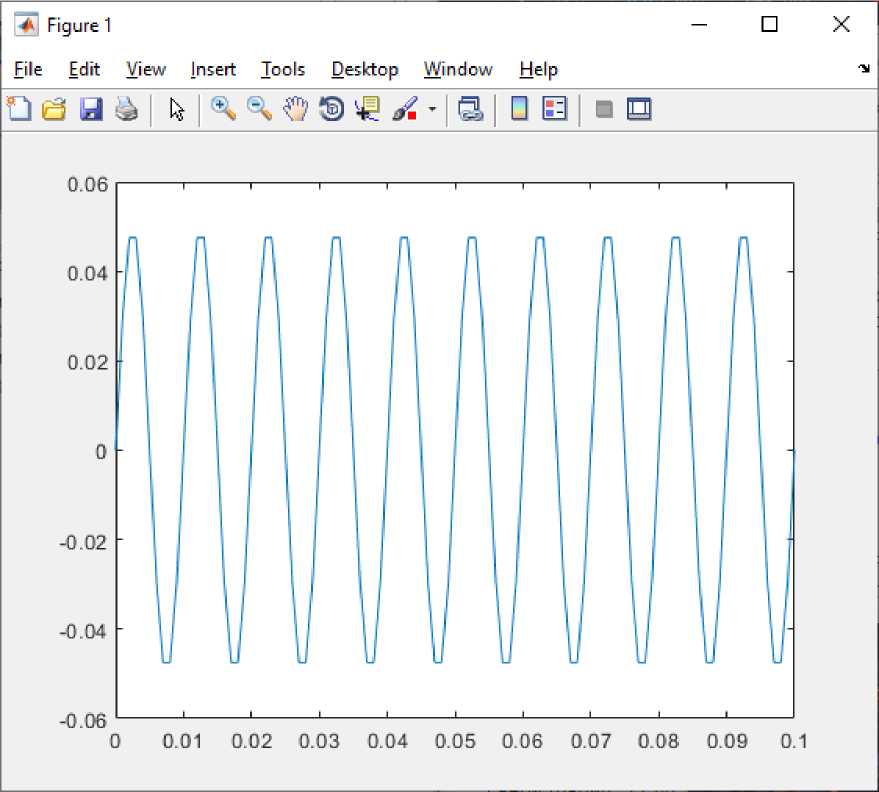
Рисунок 6 – Сигнал после применения фильтров

На рисунках видно, насколько сильно помехи влияют на передаваемый сигнал, и как изменяется сигнал после фильтрации. В итоге получили форму сигнала близкую к идеальной, то есть той, которая и была передана. Благодаря этому разработанные фильтры можно применить не только в газоанализаторах для устранения помех от сети питания и высокочастотных шумов, но и в других приборах, где нужно обрабатывать низкочастотные сигналы.

Планируется использовать разработанные программные средства после аппаратного тестирования и заводских испытаний в газоанализаторах, выпускаемых ФГУП «СПО «Аналитприбор».