Цифровые макроголограммы дисплейного типа

С появлением первых цифровых голограмм, полученных АЛоманом с сотрудниками [1], цифровая голография является предметом постоянного интереса и исследований. Большинство работ в этой области направлены на создание оптических пространственных фильтров, голографических оптических элементов для формирования лазерных пучков, проверки качества изготовления оптических поверхностей. Совсем недавно появились новые примеры применения цифровых голограмм, такие, как гибридная оптико-цифровая фильтрация и корреляция изображений и оптические нейроподобные сети. Наши исследования сконцентрированы на применении цифровых голограмм для визуализации информации: задача, которая вызывает в последнее время дополнительный интерес исследователей в связи с появившейся проблемой виртуальной реальности. В настоящее время имеются два сходящихся направления в исследовании цифровых голограмм для задачи визуализации информации. Первый метод направлен на использование только горизонтального параллакса на изображении. Этот метод подобен методу, используемому в радужной голографии. Недавно был продемонстрирован прототип компьютерного голографического дисплея, созданного на основе данного метода [2,3]. В наших экспериментах мы используем другой метод, который основан на идее синтеза субголограммы, состоящей из большого числа элементарных голограмм, воспроизводящих проекции отображаемого объекта на различные плоскости наблюдения. Мы называем такие голограммы цифровыми макроголограммами (ЦМ) для отображения информации или дисплейными голограммами. Первые эксперименты с такими голограммами, предназначенными для визуализации информации, и в частности демонстрации цифрового голографического кино, были описаны нами в конце 70-х годов [4,5,6]. В этой работе мы представляем результаты экспериментов с цифровыми макроголограммами дисплейного типа, способными восстанавливать для наблюдателя 3-мерные объекты в телесном угле ±90 градусов.

2.    Синтез и запись цифровых макроголограмм

Процесс синтеза голограмм с помощью компьютера можно разделить на 3 этапа. На первом этапе должна быть выбрана математическая модель объекта, а также геометрия его освещения и наблюдения и описаны его оптические характеристики. На втором этапе рассчитывается амплитудное и фазовое распределение световой волны, рассеянной объектом, на плоскость наблюдения. На третьей, последней стадии синтеза голограммы, полученное распределение амплитуд и фаз сначала кодируется в распределение действительных положительных чисел, а затем записывается на некоторый пространственный световой модулятор для создания голограммы, пригодной для наблюдения.

В наших экспериментах были выбраны следующая математическая модель и геометрия освещения и наблюдения:

• •    В качестве объектов были взяты две простые центрально-симметричные геометрические фигуры: куб и цепь, состоящая из пяти колец.

• •    Объект освещался диффузным светом, при этом предполагалось, что объект расположен в центре полусферы, а наблюдатель находится на поверхности этой полусферы, как показано на рис.1.

• •    Направления наблюдения задавались в сферической системе координат (p=R, ф ,0), центр которой совпадал с центром симметрии объекта. Таким образом, каждое направление наблюдения задавалось парой угловых координат (ср, 0), обычно называемых "широтой" и "долготой", соответственно.

Рис.1. Схематическая иллюстрация модели, использованной для вычисления проекций объекта, где у и 0 обозначают широту и долготу, соответственно, для данной проекции, а

Р обозначает фрагмент полусферы, соответствующий заданной широте ф и долготе 9.

Радиус полусферы или расстояние до точки наблюдения выбиралось достаточно большим по сравнению с размерами объекта, что давало возможность рассматривать объект как находящийся в дальней зоне дифракции при расчете волнового поля, рассеянного объектом на поверхность наблюдения, и тем самым позволяло упростить выполнение необходимых вычислений. На рис.1 приведен один такой фрагмент для некоторой широты ф и долготы 0 в виде заштрихованной поверхности Р. С целью дальнейшего упрощения поверхность наблюдения разбивалась на отдельные фрагменты, которые можно было считать плоскими. Для каждого такого плоского фрагмента Р(х, у)

отдельно рассчитывалось (с использованием БПФ) распределение амплитуды и фазы волнового поля, рассеянного объектом.

Для расчета проекций объекта были использованы методы компьютерной графики как наиболее подходящие для подобного рода вычислений [7,8]. Число направлений наблюдения, т.е. число проекций, необходимых для синтеза цифровой дисплейной макроголограммы, было выбрано как компромисс между требуемым качеством изображения, восстанавливаемого такой голограммой, и сложностью ее вычисления. Основываясь на предварительных экспериментах, мы выбрали наиболее подходящий интервал разбиения полусферы на фрагменты, позволяющий наблюдать плавное изменение положения объекта при изменении положения наблюдателя. Шаг дискретизации по обеим угловым координатам ф и О был выбран равным и составил 6 угловых градусов. Благодаря центральной симметрии объектов, их проекции, соответствующие широте ф=0°, совпадали с проекциями, соответствующими широте Ф=180°. Поэтому расчет проекции для ф=180° не производился. То же самое было сделано и по другой угловой координате - долготе 0. Для того чтобы получить симметрию на всем интервале наблюдения, мы сдвинули начальную точку системы координат по обеим угловым координатам на 3°. Поэтому мы использовали только 30x30 проекций объекта для синтеза ЦМ, заданные следующими угловыми координатами направлений наблюдения (Ф1=3+6ц Oj=3+6j), где 1=0,1, 2,...29 и j=0,l, 2,...29. На 2а, За и 4а приведены три примера 2-мерных проекций объекта "цепь", рассчитанные для направлений наблюдения, соответствующих следующим угловым координатам: (ф=45°, 0=45°); (ф=135°, 0=45°) и (ф=87°, 0=87°.), соответственно. Полная макроголограмма составлялась затем из таких фрагментарных или элементарных голограмм согласно расположению фрагментов на поверхности наблюдения. Если физический размер записанной элементарной голограммы превышает размер зрачка наблюдателя, который приблизительно равен 5x5 мм², то такое представление голограммы, состоящей из многих частей, адекватно естественному процессу визуального наблюдения.

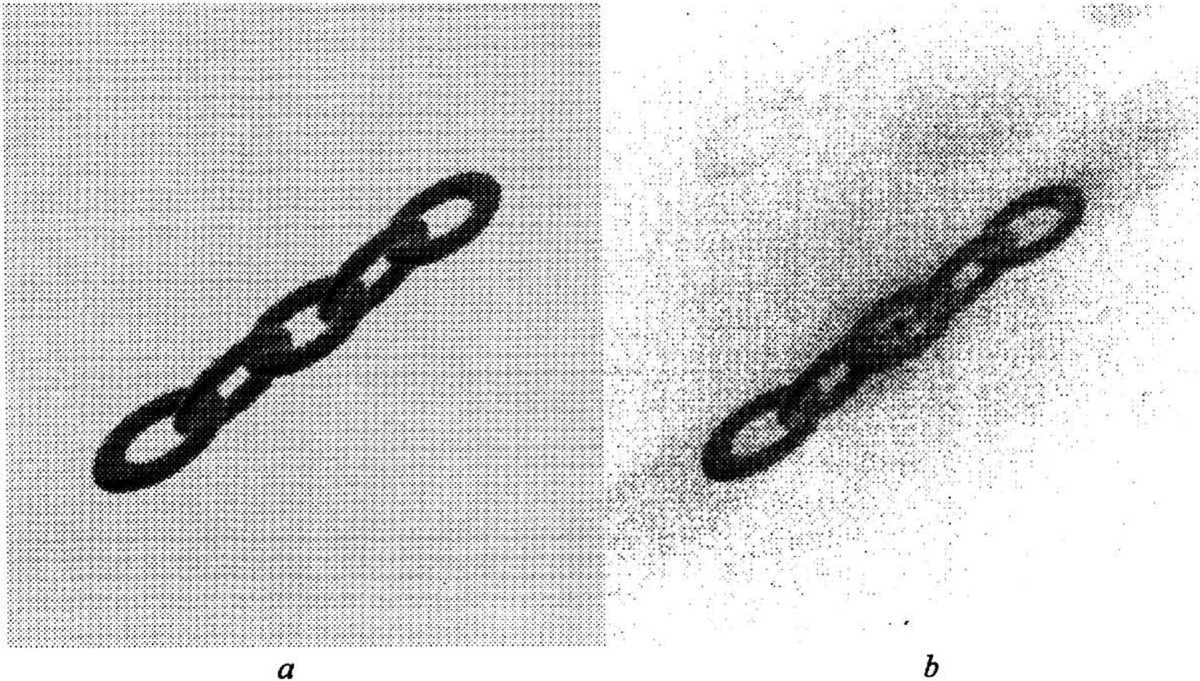
Рис 2. Проекция объекта, вычисленная для направления наблюдения, соответствующего широте ф = 45° и долготе 0 = 45:

а - 2D проекция, использованная для синтеза соответствующей элементарной голограммы; b - изображение, восстановленное с синтезированной элементарной голограммы.

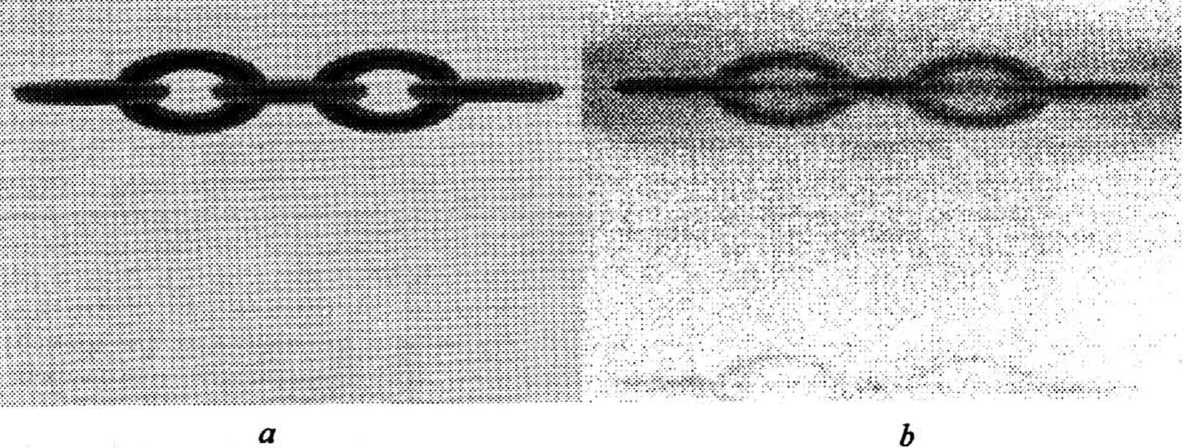
Рис 3. Проекция объекта, вычисленная для направления наблюдения, соответствующего широте ф = 87° и долготе 3 = 87:

а - 2D проекция, использованная для синтеза соответствующей элементарной голограммы b - изображение, восстановленное с синтезированной элементарной голограммы.

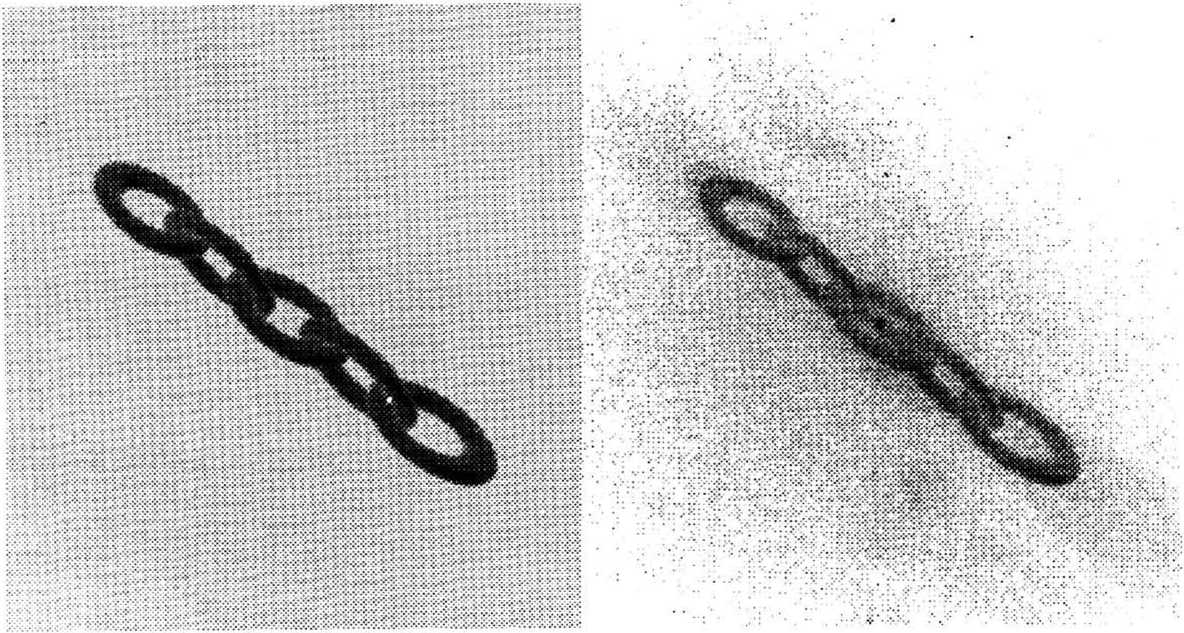
b

Рис 4. Проекция объекта, вычисленная для направления наблюдения, соответствующего широте ф = 135° и долготе 3 = 45:

а - 2D проекция, использованная для синтеза соответствующей элементарной голограммы; b - изображение, восстановленное с синтезированной элементарной голограммы.

Для кодирования цифровой голограммы мы использовали метод киноформа [9]. Согласно этому методу только распределение фазы рассеянной волны должно быть зарегистрировано на записывающей среде. Поскольку амплитудное распределение рассеянной волны не используется при таком способе записи голограммы, то неизбежные искажения в виде спекл-шума могут появиться на восстановленном изображении [10]. Для уменьшения этих искажений фаза волнового поля, имитирующая диффузное освещение объекта, вычислялась для каждой отдельной элементарной голограммы итерационным методом [11].

Синтезированная таким образом цифровая голограмма записывалась на фотографическую пленку с помощью лазерного записывающего устройства. После фотохимического проявления и отбеливания по специальной методике [12] получалась фазовая макроголограмма-киноформ, пригодная для непосредственного наблюдения.

3.    Экспериментальные результаты

В наших экспериментах были синтезированы составные цифровые макроголограммы для двух объектов: куба и цепи. Каждая голограмма состояла из 900 элементарных голограмм размером 256x256 отсчетов, которые соответствовали 30x30 ракурсам наблюдения в телесном угле ±90 градусов. Для удобства наблюдения при записи каждая элементарная голограмма повторялась 7x7 раз по горизонтали и по вертикали, и таким образом субголограмма, соответствующая одному ракурсу наблюдения, содержала 1792х 1792 отсчетов. При расчетах одного элементарного киноформа использовались 20 итераций. Голограмма была записана на фотопленку с шагом и апертурой дискретизации, равными 12,5 мкм. Размер одной элементарной голограммы был равен 3,2x3,2 мм2, а размер одной субголограммы (после 7-кратного повторения элементарной голограммы) равнялся 22,4x22,4 мм2, а величина полной макроголограммы составила 672x672 мм2. Полученные макроголограммы способны воспроизводить объекты с достаточно высоким качеством при освещении их точечным источником квазимонохроматического света. Они могут непосредственно рассматриваться из различных положений одним или одновременно несколькими наблюдателями и при смещении глаз наблюдателя по поверхности голограммы имитировать перемещение 3-мерного объекта в пространстве. На рис.26, 36, 46 приведены результаты оптического восстановления изображений проекций 3-мерного объекта с такой макроголограммы для заданных ракурсов наблюдения; соответствующие проекции синтезированного 3-мерного объекта представлены на рис.2а, За, 4а.

4.    Заключение

Мы синтезировали на ЭВМ две цифровые дисплейные макроголограммы. Каждая из дисплейных цифровых голограмм имеет размер 672x672 мм2 и содержит 2,8 Гбайт данных. Синтезированные дисплейные голограммы способны воспроизводить 3-мерные объекты в произвольном телесном угле. Создание высококачественных дисплейных макроголограмм требует от оптических сред и записывающих устройств величины разрешения порядка 108. В настоящее время не существует пространственных временных модуляторов и записывающих устройств, которые бы удовлетворяли этому требованию, за исключением фотографической пленки как среды для записи и оптикомеханических сканеров как записывающих устройств. Однако последние слишком медленны для записи голограмм в реальном времени. Мы полагаем, что быстро развивающаяся технология пространственно-временных модуляторов позволит разрешить эту проблему в ближайшем будущем.

Эта работа была поддержана Российским фондом фундаментальных исследований и Министерством науки и технической политики России.