Цифровые подходы к совершенствованию менеджмента сервисного обслуживания

Наличие очередей в системах массового обслуживания заставляет проводить исследования для определения показателей их эффективной эксплуатации, с целью существенного сокращения среднего времени ожидания при определенной длине очереди. Полученные данные можно использовать для повышения эффективности системы путем определения необходимой интенсивности обслуживания [1].

Часто такие результаты используют для совершенствования менеджмента обслуживания для минимизации его стоимостных характеристик. При этом сокращаются затраты, обусловленные потерями, вызванными задержками в предоставлении запрашиваемых услуг. К числу основных элементов моделей массового обслуживания относят посещение клиентом сервисного устройства (часто называемых "заявкой обслуживания") и продолжительность выполняемых работ ( часто называемых «сервисом» или "обслуживанием системой") [2]. Клиенты, стоящие в очередь, образуют некоторый источник. При посещении сервисного устройства, клиент может сразу же попасть на обслуживание или встать в очередь, если устройство занято. Завершив необходимый цикл работ по обслуживанию, устройство сразу же автоматически принимает очередного для его обслуживания или находится в состоянии простоя до появления нового клиента.

Цель и методы исследования

Между отдельными посещениями клиентов в сервисную структуру образуется некоторый интервал, который в целом влияет на продолжительность общего обслуживания, то есть собственно времени выполнения заявленных услуг. Структура сервиса, как правило, включает не одно выполняющее работы устройство, а несколько которые работают параллельно (например, операторы телефонной связи). Кроме того, эти устройства иногда располагают последовательно (например, обслуживание на предприятии питания включает последовательно ряд работ от поставки продуктов до их приготовления и подачи посетителю).

На рисунке 1 изображена одна из наиболее распространенных стоимостных моделей затрат на обслуживания, где общие затраты на обслуживание зависят от изменения его уровня.

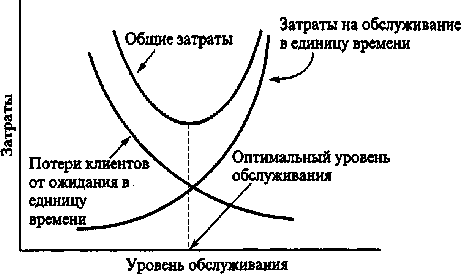
Рисунок 1 – Анализ стоимости при работе системы обслуживания

Она свидетельствует о том, что общие затраты, включая обусловленные задержками в выполнении заявленных сервисных услуг, уменьшаются до некоторого предела с возрастанием уровня обслуживания. Применение такого рода моделей достаточно условно, поскольку возникают определенные трудности оценки потерь в единицу времени, связанные с задержками в выполнении сервисных услуг.

Очередь поступающих запросов на сервисное обслуживание, может иметь конечную или бесконечную совокупность. Источник конечной мощности ограничивает число запросов, поступающих на обслуживание (например, в таксопарке, располагающем N машинами, общее количество возможных заявок на их обслуживание не может превышать N ). В то же время, например, звонки, поступающие на станцию скорой помощи, к сожалению, можно считать источником бесконечной мощности.

Особенностью систем массового обслуживания является то, что появление заявок происходит случайно. Как правило, поступление клиента или завершение сервиса мало зависит от того времени, когда завершилось обслуживание предыдущего клиента.

Указанные обстоятельства позволяют считать, что последовательные поступления клиентов, а также время их обслуживания случайны. Этот факт дает основание для количественного описания при моделировании систем массового обслуживания использовать экспоненциальное распределение с плотностью вероятности в виде

f(t) = Ле ^{-л 1} ,t> 0, где M{t} = 1/A (математическое ожидание).

В общем случае обычно изучаются системы массового обслуживания со входным потоком клиентов и выходным потоком обслуженных клиентов экспоненциально распределенными случайными величинами.

Модельные представления такого рода базируются на известных уравнениях Колмогорова [3].

Для исследования изменений вероятностных характеристик в непрерывном времени используются эти уравнения, выступая предельным случаем дискретного марковского процесса при переходе к непрерывному времени. Пусть заданы интенсивности д_лп , перехода системы из состояния п в состояние п'. При достаточно малых интервалах времени dt вероятность возникновения события перехода из одного состояния в другое для простейшего потока событий пропорциональна длине интервала: P 1 (dt) = Adt, где λ – интенсивность потока, один из элементов матрицы перехода J. Тогда имеем:

P ( t + dt ) — p ( t )                  o ( dt )

---------------= (J  — E ) P +--, dt                        dt где   Е – единичная матрица.

Переходя к пределу, получаем дифференциальное уравнение Колмогорова для условных вероятностей J, при P(0) = P₀ :

P) = ( J^T — E ) P .

dt

Основная часть

Рассмотрим следующую задачу. Пусть в некотором районе города работают две автомойки. Каждое из сервисных предприятий располагает двумя боксами, причем по имеющейся статистике обращения на обслуживание составляют для каждой примерно половину. Это вытекает из того факта, что заказы обеим автомойкам поступают с одинаковой интенсивностью, равной 28 посещениям в смену. Среднее время выполнения одной заявки составляет 30 минуты. Эти заявки поступают по закону Пуассона, а продолжительность обслуживания соответствует экспоненциальному закону. Недавно обе автомойки объединили под руководством одного владельца, который заинтересован в создании единой администрации для сокращения времени обслуживания клиентов. Возникла необходимость анализа целесообразности этого объединения.

Используя теорию массового обслуживания, автомойки можно считать сервисными устройствами, которые оказывают определенную услугу клиентам. Каждая мойка может быть представлена моделью с λ = 28 посещениями в смену и g = 420/(2^30)= 7 интенсивностью работы бокса автомойки. Объединение служб автомоек приведет к модели с A = 2 • 28 = 56 посещений в смену и μ = 7 интенсивностью работы автомойки в час.

Те же расчеты справедливы для задачи в случае, когда в многоканальной системе имеется s сервисных устройств для выполнения запросов клиентов.

Одним из случаев системы массового обслуживания является система включающая очередь. Для такого варианта многоканальной системы рассматривают количество клиентов, запрашивающих сервис, рассчитанный на п>0 в общем случае заявок (рис. 2). При этом, когда количество заявок больше числа каналов, то следующий клиент ожидает очереди на обслуживание. В случае превышения числа заявок в системе числа s+ n, клиент покидает систему.

X X X X XX XX

P 2ц Зц (S —1}ц зц зц зц Зц

Рисунок 2 – Схема обслуживания в многоканальной системе с очередью

Для такой системы уравнения Колмогорова могут быть записаны в виде:

dP0

• -= =-AP₀ + ^P i , dt

dPk

= A^P k—i ^— (Л + ky}^P k + ^(k + l)^^P k+i , к at

= 1,2, -,s;

dPk

—- = —A^P k—i ^{- (}A + s^^)P k + s^^P k+i , i dt

= s + 1,2, .„, s + n — 1;

^dP s+n   ~            „

= ^P s+n-1 ^{— s}^^P s+n ^.

По сравнению с ранее рассматриваемой системой без очереди уравнения необходимо дополнить следующими условиями:

• 1)    общее число клиентов в очереди:

_       ^s+1

^{U   (}s — 1)!(s — ^)

• 2)    предполагаемое число клиентов в сер-

• висе:

fi = v+ ^;

• 3)    ожидаемое время выполнения заявки:

t = л;

• 4)    фактической время обслуживания:

  и

  
  

  ^^^^^»

  
  

T=-x

Целесообразной мерой для сравнения двух вариантов предлагаемой услуги является примерное время ожидания от момента приезда клиента до момента начала обслуживания автомобиля, которое можно обозначить Wq. Проведенные расчеты показывают, что время ожидания обслуживания автомобиля оказывается 0.53 часа (примерно 32 минуты) для модели обслуживания с двумя автомойками и 0.24 часа (примерно 14 минут) для модели обслуживания в объединенном варианте. Значительное уменьшение (более чем на 50%) расчетного времени рассмотренной сервисной системы подтверждает целесообразность объединения двух автомоек.

Расчет функционирования многоканальной системы c очередью можно осуществить в пакете прикладных программ Mathcad. Одна из таких программ приведена на рис. 3.

На рисунке 3 приведен характерный график изменения вероятности простоя (z i,1 ) и вероятности отказа системы (z i,n+s+1 ) в процессе сервисного обслуживания для ранее определенных параметров n=0, s=2, λ= 28 и μ=7.

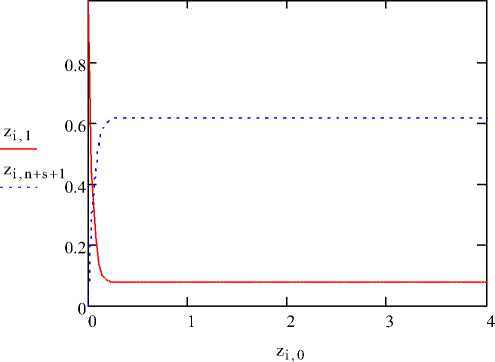
Рисунок 3 – Динамика изменения системы массового обслуживания для назначенных управляющих решений (n, λ, μ)

Выводы

Анализ расчетных данных говорит о том, что при достаточно малых вероятностях простоя (z i,1 ) вероятности отказа системы (z i,n+s+1 ) достаточно значимы. Это свидетельствует о необходимости совершенствования системы, например, путем ее объединения с родственным сервисом.