Циклические группы в колокольном звоне

Method ringing, known as scientific ringing, is the practice of ringing the series of bells as a series of permutations. A permutation f: 1, 2, ..., n → 1, 2, ..., n, where the do- main numbers represent positions and the range numbers represent bells. f (1) would ring the bell first and bell f(n) last. The number of bells n has n! possible changes.

Figure 1. Pain Bob Minimus Permutation

The bell ringer cannot choose to ring permutations in any order because some of the bells continue to ring up to 2 seconds. Therefore, no bell must be rung twice in a row. These permutations can all be played until it eventually returns to the original pattern of bells.

A common permutation pattern for four bells is the Plain Bob Minimus permutation (Figure 1). The Plain Bob pattern switches the first two bells then the second set of bells. They would start the bell ringing with 1234. The first bell would go to the second position and third would go to the fourth; therefore, the next bell combination would be 2143. The next bell switch would be the two middle bells. Therefore, the bell 2143 would turn to 2413. The bell ringers would repeat this pattern of switching the first two and second two, followed by switching the middle until about 1/3 of the way through the permutations. At the pattern 1324, we cannot switch the middle two. If we switched the middle two, we would get back to 1234. Therefore, the bell ringers figured out to switch the last two bells every 8 combinations. Then after 24 moves (4!) we get back to the bell combination of 1234. Since we made rotations of the bells and generated every combination of the set and are now back at the beginning, we can say that the bell ringing pattern is cyclic.

Figure 2. Permutation of 4 bells

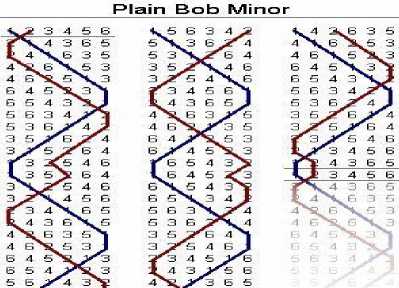
Figure 3. Permutation of 6 bells

There are other ways to cover all of the permutations without using the Bob Minimus method (Figure 2). Bob Minimus method is used because it is easy for bell ringers to accomplish because they do not have sheet music. Another common permutation method is following the last bell and moving it over one space to the left each ring then after it is on the left moving it back over to the right (Figure 3).

You can create a cyclic group with any number of bells. However, the more bells you add the longer the cycle will take. Assuming that each bell ring takes 2 seconds,

Someone can complete a set of three bells in 12 seconds. If we have 9 bells it could take up to 8 days and 10 hours.

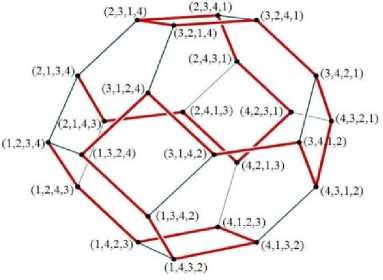
Figure 4. Hamiltonian graph of the permutation 4 bells

The bell permutations can be expressed as a Hamiltonian graph. A Hamiltonian path is an undirected or directed graph that visits each vertex exactly once. The Hamiltonian circuit can be drawn as a simple circuit that has a circular path back to the original vertex. Hamiltonian circuits for the symmetric group

S n mod cyclic groups Z n correspond to the change ringing principles on n bells.

Conclusion

Human minds are designed for pattern recognition and we can find algebraic structures in common objects and things around us. Cyclic groups are the simplest groups that have an object that can generate the whole set. The object can generate the set by addition, multiplication, or rotations. Cyclic groups are not only common in pure mathematics, but also in patterns, shapes, music, and chaos. Cyclic groups are an imperative part of number theory used with the Chinese remainder theorem and Fermat’s theorem. Knowing if a group is cyclic could help determine if there can be a way to write a group as a simple circuit. This circuit could simplify the process of generation to discover the most efficient way to generate the object for use of future applications in mathematics and elsewhere. As we know the human life direct and indirect have close relationship with mathematics, here we mentioned the application of cyclic group in Bell Ringing which is match important in our life.