Code Formal Verification of Operation System

Published Online December 2010 in MECS

With the increasing pressure on non-function attributes (security, safety and reliability) requirements of operation system, high–confidence operation system is becoming more important. In manufacturing, defense, traffic, aviation, space flight, critical infrastructure control, automotive systems, medical service, assisted living and other key application domain, there have been lots of tremendous losses caused by the system failure which the core control software design flaws brought about. As accidents caused by software error or failure are becoming more and more, people come to realize that the system under the condition of high complexity, conventional software engineering methods and software design, evaluation method cannot solve embedded software reliability and safety design problems in depth. This calls for end-to-end guarantees of systems functionality, from applications down to hardware.

While high–confidence certification is increasingly required at higher system levels, the operating system is generally confident to be correct. The correctness of the computer system can only be as good as that of the underlying Operation System (OS) kernel. The kernel, defined as the part of the system executing in the most privileged mode of the processor, has unlimited hardware access. Therefore, any fault in the kernel’s implementation has the potential to undermine the correct

Manuscript received; revised ; accepted. corresponding author ： Yu Zhang.

operation of the rest of the system. Worse still, numerous fixes, distributed by their vendors, may introduce new errors or render other system components inoperative.

The only real solution to establish trustworthiness is formal verification. There are many kinds of verification work, which focuses on high level design. There exists the gap between design and implementation. In a sense, implementation is more important than design. Proving the implementation correctness is approach to build high-confidence OS. It’s about explicit and strict mathematical proofs of the correctness of a system. This has, until recently, been considered to be an intractable proposition — the OS layer was too large and complex to poorly scale formal methods. However, there is a renewed tendency towards smaller OS kernels means that the size of the program to be verified is only around 10,000 loc [1, 2]. It is possible to use formal verification instead of traditional methods for this area. The combination of low-level, complex property, roughly 10,000 loc is still considered intractable in industry. In this paper we research on formal verification of this smaller OS kernel in system implementation level, which is a weak link in the trustworthy of OS kernel and is related to system eventually correctness.

The next section provides an overview of OS verification and its application to kernels. Section 3 gives a more detailed two different formal verification methods for C program. Section 4 present a case study to the verification of real-world C systems code derived from an implementation of µ C / OS - II , which not only provides an opportunity to validate the models against realistic code, but also allows us to compare and contrast the two methods in practice. Section 5 summarizes our work and prospect.

• II.    OS verification

To get an impression of the current industry best practice, we look through the software assurance standard: RTCA/DO-178B and Common Criteria. RTCA/DO-178B [3] is an industry-accepted guidance for satisfying airworthiness requirements which provides guidelines for the production of software for airborne systems and equipment. Systems are categorized by DO-178B as meeting safety assurance levels A through E based on their criticality in supporting safe aircraft flight. Systems are categorized by DO-178B as meeting safety assurance levels A through E based on their criticality in supporting safe aircraft flight. The level A is catastrophic failure protection and level E is minimal failure protection. Software/System assurance levels are shown in Fig.1.

⟡ Level A: Catastrophic Failure Protection

⟡ Level B: Hazardous/Severe Failure Protection

⟡ Level C: Major Failure Protection

⟡ Level D: Minor Failure Protection

⟡ Level E: Minimal Failure Protection

• Figure 1. Software/System assurance levels.

And Common Criteria [4] is the other standard for software verification that is mutually recognized by a large number of countries. It textual research software level from the methodological perspective and the software artefacts are: the software requirements, the functional specification, the high-level design of the system, the low-level design, and finally the implementation. There are seven levels of assurance (EAL 1–7) in the standard, which generate partitions by the treatment of each software artefact. None of currently commercially available OS kernels has been formally verified. Three popular ones including Trusted Solaris, Windows NT, and SELinux have been certified to Common Criteria EAL 4, but this level does not require any formal modeling and is not designed for systems deployed in potentially hostile situations.

Formal verification makes sure that software fulfils its specification. It’s believed that OS formal verified completely is high-confidence. Formal verification of OS code has so far been considered prohibitively expensive, or even impossible. In recent years, this view has been changing and there are some verification projects that target realistic amounts of system code. Here we review two main projects.

The Verisoft [5] project is a large-scale effort to demonstrate the pervasive formal verification of a whole computer system from the hardware up to application software. It is a long-term research project funded by the German Federal Ministry of Education and Research (BMBF). The main goal of the project is the pervasive formal verification of computer systems. The project focused on implementation correctness. The main code verification technology used in this project was developed by Schirmer [6]. The tool is a generic environment in the theorem provided by Isabelle [7] for the verification of sequential, imperative programs that can be instantiated to a number of different languages. The tool set includes a Floyd–Hoare–style logic for program verification. These semantic levels are connected to each other by equivalence proofs. The verification environment also integrates with tools such as software model checkers that can automatically discharge certain kinds of proof obligations, thereby reduce the manual proof effort.

Recently, NICTA from Australia has made an OS verification project named L4.verified [8, 9]. The project is providing a mathematical, machine-checked proof of the functional correctness of the seL4 microkernel with respect to a high level, formal description of its expected behavior. And the aim is to produce a truly trustworthy, high-performance operating system kernel. The seL4 kernel design was integrated tightly with two teams: NICTA OS group and L4.verified group. So that while the design was mainly driven by the NICTA OS group, the concurrent verification effort in L4.verified provided continuous, early feedback that was taken into account by the design group. They think starting the verification directly from the C source without any higher-level specification should be expected to be a difficult and long process. In contrast to the OS approach, the traditional formal methods would take the design ideas, formalize them into a specification first and then analyze that specification. Based on this, C-level implementation verification only needs to verify functional correctness.

Formal verification can reduce the larger gap between user requirements and implementation and hence gain increasing confidence in system correctness. It makes others convince that the implementation of software fulfils its specification. Therefore, system correctness is described by means of a formal method, then the standard procedure through certain validation rules of these formalization specifications and relevant code verification, judge whether the program in accordance with the procedure specification indicated by the way of implementation.

In the program verification field, predicate abstract method [10] presented by Graf is a kind of program oriented model abstract methods, which abstract program into finite state machine model based on a set of limited quantity predicate and then can use model-checking tool to verify. Combined with CEGAR ( Counter-Example Guided Abstraction Refinement ) method [11], model establishment and verification methods based on predicate abstract can verify software source code automatically. PCC (Proof - Carrying code) [12] and FPCC (Foundational Proof - Carrying code) [13] based on logical method, through carrying the proof of source codes, provides a mechanism that guarantee the safety of code before run. Due to lack of type expression ability the, PCC itself will only verify program’s simple attributes such as type safe. CAP [14] makes the program in the most general attributes can be verified by improving PCC expression. It is program verification method based on Hoare logic style in the assembly level.

• III.    verification method

Takes theorem proving and model-checking as the main technical methods to resolve the key techniques of verifying OS microkernel. The details are as follows.

• A.    Theorem Proving

We adopt program correctness validation technology based on Hoare logic [15] to establish the axiom semantics of C program. And then, use Coq as an interactive theorem proving tool to prove program correctness.

Hoare logic provides a formal system for reasoning about program correctness. Hoare logic is based on the idea of a specification as a contract between the implementation of a function and its clients. The specification is made up of a pre-condition and a postcondition. The pre-condition is a predicate describing the condition the function relies on for correct operation; the client must fulfill this condition. The post-condition is a predicate describing the condition the function establishes after correctly running; the client can rely on this condition being true after the call to the function. Hoare logic uses Hoare Triples to reason about program correctness. A Hoare Triple is of the form [P]S[Q] or {P}S{Q}, where P is the pre-condition, Q is the postcondition, and S is the statement(s) that implement the function.

Definition 1(termination): if each input a that makes P(a) true, program S will terminate, said the program S is terminated to P. Use Sterminate to stand for it.

Definition 2(partially correct): if S is executed in a store initially satisfying P and it terminates, then the final store satisfies Q. Use [P]S[Q] to stand for it. Partially correct form: [P]S[Q] iff ( ∀ a)(P(a)and(Sterminate)) → Q

Definition 3(totally correct): assuming the P is satisfied before S executes, the S is guaranteed to terminate and when it does, the post-condition satisfies Q. Thus total correctness is partial correctness in addition to termination. Use {P}S{Q} to stand for it. Totally correct form: {P}S{Q} iff ( ∀ a)(P(a) → ((Sterminate) and Q)

And some rules of Hoare logic are as follows:

skip：{P}skip{P} assign：{P[x a a]}x := a{P}

{P}S1{Q}，{Q}S2{R} sequence：

{P}S1；S2{R} if：     {b∧P}S1{Q},{b∧P}S2{Q}

{P}if(b)then(S1)else(S2){Q} while：            {b ∧P}S{P}

{P}while ( b ) do ( S ) { b ∧ P}

P → P 1 ， {P}S{Q} ， Q 1 →Q {P 1 }S{Q 1 }

The main approach of verification is translated C program to formal language in a logic reasoning system. The translation is base on axiom semantics of C program. And we chose Hoare logic. The main steps of our program verification include: program designers provides additional properly assertion for program, and then generates verification conditions and theorem prove assistant completes the proof of verification conditions. The verification processes are shown in Fig.2. Here are the main steps in detail.

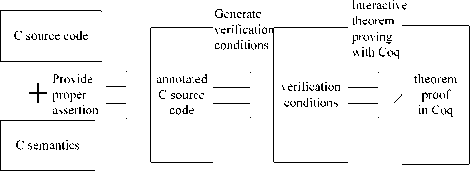
Figure 2. verification processes.

( 1 ) Provide proper assertion

Proper assertions embody program semantics. We can’t directly analyze source code mechanically now. The automatic generation of loop invariants is still an unsolved problem. It refers to solving a fixed point of recursive formula, and solving this equation is usually undecidable. And a useful loop invariant precisely expressed relationship between variables which are operated by looping statements in program body. However, searching for an effective loop invariant is full of challenges.

Therefore, the source code needs the programmer to provide the appropriate assertions, including the entrance of function, the exit of function and loop invariant. Through this process, C source code is translated into annotated C source code. Providing proper assertion will simplifies the proof and benefit for follow-up machine-checkable proof.

( 2 ) Generate verification conditions

Hoare logic constructs a contract between the implementation of a function and its clients. But search of its pre-condition is very difficult. Therefore, we use the weakest pre-predicate logic to calculus the pre-condition in Hoare logic. In this way, we can get pre-condition mechanically. The weakest pre-condition calculus [16] is proposed by Dijkstra which is used to perform program correctness proof and reason about the program.

Weakest pre-condition: wp(S,Q) = M, set of states M for which:

• -    M is started in state m ∈ M,

• -    M halts in state t where Q(m).

Its basic idea is in order to verify {P}S{Q} we need to find out all P ′ called Pre(S, Q), which make {P ′ }S{Q} established. Verify that ( ∃ P ′ ) P ′∈ Pre(S, Q), P ⇒ P ′ . In these P ′ ， look for a weakest pre-condition ， and take it as the pre-condition of the program. Therefore proof process becomes to calculate WP(S, Q), and prove P ⇒ WP(S, Q) ： {P} S {Q} ⇔ ( P ⇒ wp(M,Q))

Here are the rules of weakest pre-condition:

WP(skip,Q)=Q

WP(“x = E”, Q) = Q[E/x]

WP(“S1;S2” , Q) = WP (S1, WP(S2, Q))

WP(IF B {S1} else {S2}, Q) = (B ⇒ WP(S1, Q)) ∧ ( B ⇒ WP(S2, Q))

WP(while B {C }, Q ) = I ∧ ( I ∧ B ⇒ VC(C, I) ) ∧ (I ∧ B ⇒ Q ) ， I is loop invariant ， B is loop condition.

Verification conditions are generated mechanically according to the weakest pre-predicate logic. Through this process, annotated C source code is translated into a series of verification conditions. Since we use the weakest prepredicate logic to calculus the pre-condition in Hoare, therefore this verification conditions needn’t to be proved except for three type conditions (the entrance of function, the exit of function and loop invariant).

( 3 ) Interactive theorem proving

Theorem proving method with high abstractions can process infinite state system theoretically. We use high order logic to describe the system and the system properties. Then transfer properties to be verified into theorem described by mathematical logic. In the end, use theorem proof assistant Coq [17] with axioms, proved theorem and reasoning rules to verify specification is correct in high order logic system.

Coq is a theorem proof assistant based on high order logic, which is develop by INRIA using Objective Caml language. The tool is based on the logical frame CiC (Calculus of inductive Constructors) , which is typed lambda calculus. Due to good implementation of Coq and powerful expression ability of CiC, Coq has been widely used in programming language theory research fields, such as meta programming language theory, formal analysis frame theory, program verification etc.

Coq provide an abundant strategies library. For the same goal, we can adopt different strategies or strategy combinations to complete proof. Thus the choice of strategy is very important to the proof process. Coq has powerful development function. In Coq, we can formally definition our own logic system, reasoning system, etc. We formal defined our reasoning rules in Coq. Fig.3 is shown the definition.

forall (P : Eprop), correct skip P P forall v e (P Q : Eprop), (forall E, P E -> Q (upd E v (eval E e))) -> correct (assign v e) P Q forall s1 s2 P P' Q, correct s1 P P' -> correct s2 P' Q -> correct (seq s1 s2) P Q forall e s I, correct s (fun E => I E /\ eval E e <> 0) I -> correct (while e s) I (fun E => I E /\ eval E e = 0)

forall e s1 s2 P Q, correct s1 (fun E => P E /\ eval E e <> 0) Q -> correct s2 (fun E => P E /\ eval E e = 0) Q -> correct (br e s1 s2) P Q forall s (P P' Q Q' : Eprop), (forall E, P E -> P' E) -> (forall E, Q' E -> Q E) -> correct s P' Q' -> correct s P Q.

• F igure 3. Definition of Hoare logic in Coq.

Coq uses interactive method with users to complete proof. Strategies proof and proof check reduce the proof complexity and realize the automation of proof to a certain extent. Since Coq provide lots of proof strategies for the user to choice, therefore users can decompose difficult proof into a series of lemma and choose proper strategies according to problem. Coq use reverse reasoning method. According to the input strategy decompose current given target proof goal to a series of simple objectives, then through constructing sub-targets proof get the whole goal of proof, finally through the proof checker to check the correctness of the proof.

• B.    Model Checking

Model checking is a formal verification method. It is able to determine the validity of a specification for all possible states or execution paths in a software system to which it is applicable. Given any finite M and specification f check that M is a genuine model of the specification f: M |=f. It enjoys substantial automation support. It has been quite successful for hardware verification.

Model checking works on a model of the system that is typically reduced to what is relevant to the specific properties of interest. The model checker then exhaustively explores the model’s reachable state space to determine whether the properties are held. It is an automatic verification method, and can provide counterexample path when some properties are not satisfied. The general model checking tools required to use their special modeling language. So when you use these tools, you must abstract system model manually.

Model checking is only feasible for systems with a moderately-sized state space, which implies dramatic simplification. Hence, this approach usually does not give guarantees about the actual system.

There are two major challenges in practical and scalable application of model checking to software systems. The first challenge is the applicability of model checking. Generally, there are significantly different between the input formal representations of model checkers and the widely used software representations. In addition, software systems often have infinite state spaces while model checkers are often restricted to finite state systems. The second challenge is the intrinsic complexity of model checking. The number of possible states and execution paths in a real-world software system can be extremely large, which makes naive application of model checking to such a system intractable and requires state space reduction. So we apply two model checking tool try to verify C code.

Therefore, direct model checking for software program is based on model abstraction, which abstracts the finite state space model from program. Based on the predicate abstract, modeling and verification of source code can be automatic. BLAST [18] is a model checking tool for C program, which developed by Berkeley California university. This tool is based on a counterexample automatically abstract refinement technology to construct abstraction model. It uses lazy predicate abstraction and interpolation-based predicate discovery methods to abstract ，verify and refine the state space of program. This tool can not only verify security attributes of sequence C program, but also verify concurrent C program. And use theorem proof assistant Simplify to solve abstract state transition relationship. Model checking has been applied to the OS layer and has shown utility here as a means of bug discovery in code involving concurrency. So we try to use BLAST to verify OS kernel.

SPIN [19] is an efficient model checker for models of distributed software systems. It has been used to detect design errors in applications ranging from high-level descriptions of distributed algorithms to detailed code for controlling telephone exchanges. SPIN accepts design specifications written in the verification language Promela (a Process Meta Language), and it accepts correctness claims specified in the syntax of standard Linear Temporal Logic (LTL) [20]. The verification languages of SPIN, Promela, more resembles a programming language than a modeling language. SPIN accepts correctness properties expressed in linear temporal logic (LTL). Vardi and Wolper showed in 1983 that any LTL formula can be translated into a Büchi automaton. SPIN performs the conversion to Büchi automata mechanically based on a simple on-the-fly construction [21].

LTL is a prominent formal specification language that is highly expressive and widely used in formal verification tools. LTL provides the temporal operators next (X), Future (F), Globally (G), until (U), weak-until (W), and release (R). Below is Requirement Specification BNF-grammar.

φ::= T |⊥ p |φ| (φ∧φ) | (φ∨φ) | (φ→φ) |(Xφ) |(Fϕ) |(Gφ) |(φUφ) |(φWφ) |(φRφ)

Where p is LTL formulas.

A Büchi automaton (BA) is a tuple (Q, ∑ , δ, q 0 , F) where:

• -    Q is a finite set of states

• - ∑ is an alphabet

• - δ: Q ^× ∑ → 2 ^Q is a transition function and

• -    q 0 ∈ Q is a set of initial states

• -    F ⊆ Q is a set of accepting states

The set of executions accepted by a BA is called the language of the BA. Languages of BAs represent a superset of those of LTL; every LTL formula can be represented by a BA. When a BA is generated from an LTL formula, the language of the BA represents only the traces accepted by the LTL formula. For example the BA in Fig. 4 represents the language accepted by the LTL formula (φ 1 U φ 2 ).

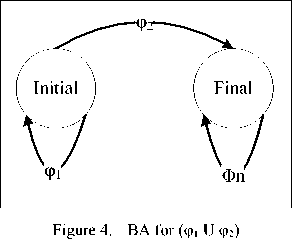
This formula specifies that φ 1 holds in the initial state of the computation or in the current state and (φ 1 U φ 2 ) holds in the next state. The language of the BA in Fig.4 accepts the set of traces {φ 1 φ 2 ..., φ 1 φ 1 φ 2 ..., φ 1 φ 1 φ 1 φ 1 φ 1 φ 2 ...}. Notice that each of these traces passes through the accepting state Final. Temporal operators until (U) require φ 2 satisfy in the future and don't involve anything occurred after φ 2.

• IV. Case study

  In this paper we present a case study in the application of our models to the verification of real-world C systems code (Os_Core.c) derived from an implementation of µ C / OS - II [22]. The µ C / OS - II is a low-cost priority-based pre-emptive real time multitasking operating system kernel for microprocessors, written mainly in the C programming language. It is mainly intended for use in embedded systems. Featuring such elements as preemptive multitasking, unlimited number of tasks and priorities, and round robin scheduling of tasks at equal priorities. Since published in 1992, it has been widely used all over the world. So we choose this OS kernel to verify. Function is shown in Fig.5.

This function is used to prevent rescheduling to take place. This allows your application to prevent context switches until you are ready to permit context switching. µ C / OS - II define two macros to deal with interrupt switch: OS_ENTER_CRITICAL() and OS_EXIT_CRITICAL(). When access critical sections, must use OS_ENTER_CRITICAL() to open interrupt, then use OS_EXIT_CRITICAL() before leave critical sections. This mechanism has three different implementations. In some special hardware, first implementation is the only choice. So we take this implementation.

* PREVENT SCHEDULING

*

* Description: This function is used to prevent rescheduling to take place. This allows your application to prevent context switches until you are ready to permit context switching.

*

* Arguments : none

*

* Returns : none

*

* Notes : 1) You MUST invoke OSSchedMutex() and OSSchedUnMutex() in pair. In other words, for every call to OSSchedMutex() you MUST have a call to OSSchedUnMutex().

#define OS_CRITICAL_METHOD 1

• #if OS_SCHED_MUTEX_EN > 0

void OSSchedMutex (void)

{

• #if OS_CRITICAL_METHOD == 3

  /* Allocate storage for CPU status register */ OS_CPU_SR cpu_sr;

#endif if (OSRunning == TRUE) {

/* Make sure multitasking is running*/

OS_ENTER_CRITICAL();

if (OSMutexNesting < 255) {

/* Prevent OSMutexNesting from wrapping back to 0*/

OSMutexNesting++;

/* Increment Mutex nesting level*/

}

OS_EXIT_CRITICAL();

}

}

#endif

Inductive correct : Stint -> Eprop -> Eprop -> Prop : =

| okNil : forall (P : Eprop), correct nil PP

| okAssign : forall v e (P Q : Eprop),

(forall E, P E -> Q (upd E v (eval E e) ) )-> correct (assign v e) P Q

| okSeq : forall si s2 P P1 Q, correct si P P1 -> correct s2 P1 Q -> correct (seq si s2) P Q

| оkWhlie : forall e s I, correct s (fun E => I E /\ eval E e <> 0) I -> correct (while e s) I (fun E => I E /\ eval E e = 0)

| okEr : forall e si s2 P Q, correct si (fun E => P E /\ eval E e <> 0) Q -> correct s2 (fun E => P E /\ eval E e = 0) Q -> correct (br e si s2) P Q

I okConseq : forall s (P P1 Q Q1 : Eprop), (forall E, P E -> P1 E) -> (forall E, Q1 E -> Q E) -> correct s P1 Q1 -> correct s P Q.

Definition OSSchedMutex_pre(mutex : Var):Eprop : = fun E => E mutex=0.

Definition O55chedMutex_post(mutex : Var):Eprop:= fun E => E mutex=l \/ E mutex=0.

Definition OSSchedMutex prog(mutex: Var):= br(C(equal_0 mutex)) (mutex <- (C l))nil. Theorem OSSchedMutex ok:correct(

OSSchedMutex_prog VX)(OSSchedMutex_pre VX)(OSSchedMutex_post VX). Proof.

• Figure 6.    Definition in Coq.

apply okEr.

apply окAs sign.

unfold OSSchedMutex pre in |- *.

unfold upd in |- *.

slmpl in |- *.

intuition.

unfold OSSchedMutex_pre, OS5chedMutex_post in |- *.

unfold upd in |- *.

simpl in |- *.

intuition.

apply okConseq with (fun E : Env => E VX = 0 /\ 0 = 0) (fun E : Env => E VX Ci /\ 0 = 0) .

intuition.

apply okNil.

OSSchedMutex ok is defined

Figure 5. C source code.

• Figure 7.    Proven strategy.

• A.    Theorem Proving Approach

According to theorem proving approach, program designers provide additional proper assertion for the program, then generates verification conditions and theorem proof assistant completes the proof of verification conditions. Here we analysis reasoning process in Coq. This process is shown in Fig.6.

For mutex_ok theorem, we prove it with Hoare logic reasoning and rich strategy libraries provided by Coq. We should prove every objectives generated by each proof step. When all targets have been proved, mutex_ok will be proved successfully. Details are shown in Fig.7.

We abstract theorem (verification) from C program based on axiom semantics. The result shows that mutex_ok theorem is correct. So it means that this C program fulfils its specification. From the case, we can see that although the scale of code is not big, the cost of verification is expensive. And if our strategy library is power enough, the automation degree of proof will increase.

• B.    Model Checking Approach

Model checking approach is utilizing two modelcheckers, BLAST and SPIN, to analyze and verify C program. We take research in the modeling method based on C program and the formal specification method which use LTL or CTL to description system attributes. We mainly focus on ensuring the program correctness and safety requirements.

( 1 ) Verification with BLAST

In order to detect the program sequence security attributes, we usually need to add the corresponding observation variables and statements in the program to get to observe the value of the variable. In this case, the global variable Mutex is used to mark whether OS_ENTER_CRITICAL () or OS_EXIT_CRITICAL () is used alternately. BLAST uses relatively independent code description language to detect the sequence security attributes, which can protect the integrity of the source code as far as possible. Fig.8 shows the specification document.

global int Mutex= 0;

event { pattern { OS_ENTER_CRITICAL(); } guard {Mutex== 0 } action {Mutex= 1; }} event { pattern { OS_EXIT_CRITICAL();} guard { Mutex== 1 } action { Mutex = 0; }}

Figure 8. OS_ENTER_CRITICAL().spc.

According to the concept of mutually exclusive, continuous twice to lock or unlock critical area is impracticable. When the program is invoked, OS_ENTER_CRITICAL (twice) or OS_EXIT_CRITICAL () function will trigger the Mutex variables and then trigger ERROR tags. After this, use BLAST command to check the program. This is shown in Fig.9.

Figure 9. OS_ENTER_CRITICAL().spc.

When BLAST finishes the check, it returns the result. The result of the souce code is that the system is safe. Fig. 10 shows the result.

Mutex==0

Mutex ==1

Read 2 predicates

Begin Building CFA ……

Finished Building CFA …… addPred: 0: (gui) adding predicate Mutex ==0 to the system addPred: 1: (gui) adding predicate Mutex ==1 to the system Forking Simplify process ……

No error found. The system is safe :-)

• Figure 10.    Check result.

( 2 ) Verification with SPIN

Through establishing Promela model of source code (Os_Core.c), we use model checker SPIN to analyze and verify the correctness of the code. We mainly focus on temporal safety proper. We simulate function calls into process. And we specify process interactions by channel to transfer function invocation (parameters transfer and return values). Promela model is shown in Fig.11 shown.

#define OS_Is_Running 1

#define OS_Not_Running 2

int LOCK= 0;

chan ENC=[1] of {byte};

chan EXC=[1] of {byte};

chan ETX=[1] of {byte};

chan returnvalue=[1] of {byte};

proctype OSSchedMutex(int OSRunning, OSMutexNesting) { byte Mutex;

if

::(OSRunning==1)->returnvalue!OS_Is_Running

::else->returnvalue!OS_Not_Running;

fi;

if

:: (OSRunning==OS_Is_Running)->ENC?Mutex;

if

::(Mutex==1);

if

:: (OSMutexNesting < 255)->OSMutexNesting ++; if

:: EXC?Mutex;

fi;

fi;

fi;

fi;

assert(LOCK==0);

} proctype OS_ENTER_CRITICAL()

{ if

::(LOCK==0)->LOCK=1;ENC!1;ETX!1;

::else->ENC!0;

fi;

} proctype OS_EXIT_CRITICAL()

{ if

::ETX?1;

if

::(LOCK==1)->LOCK=0;EXC!0;

::else->EXC!1;

fi;

fi;

} init

{ int x;

run OS_ENTER_CRITICAL();

run OSSchedMutex(1,10);

run OS_EXIT_CRITICAL();

returnvalue?x;

printf("return: %d\n", x)

}

• Figure 11.    Promela model.

We established three processes with four channels. Process OSSchedMutex simulates main function of source code, process OS_ENTER_CRITICAL and process OS_EXIT_CRITICAL simulate synchronization relationship inter-process. The three processes are executed synchronously by channel. We run simulation execution of this program in SPIN. The sequence of simulation execution is shown in Fig.12.

Then we verify this program in SPIN. SPIN generates a parser. The parser will be compiled and executed. Result of Verification will be displayed in the Verification Output window. If everything is normal, the result show no errors be found. And if there are some conditions without the right reach in execution, these statements will be highlighted in the main window. And we can run the counter-example in guided simulation. Output of verification is shown in Fig.13. There are no error find in the code.

We express the correctness requirements in LTL formulae by using the following definitions of propositional symbols: #define p (LOCK==0). And then use LTL formulae” <> p” to check whether this program is correctness as we specified. Verification result is shown in Fig.14.

SPIN is a generic effective verification system that supports the verification of asynchronous process systems. SPIN verification models are focused on proving the correctness of process interactions. Since SPIN uses its special modeling language Promela to model system, therefore we must abstract and model the system manually: transfer C to Promela. Using this manual method, modeling is complex and prone to making mistake. BLAST is not so. It is oriented software source program C. It can analyze C program mechanically. It is based on model abstraction, namely abstract the finite state space from program.

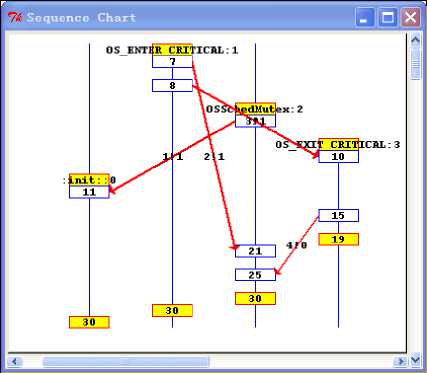
Figure 12. Sequence chart of simulation.

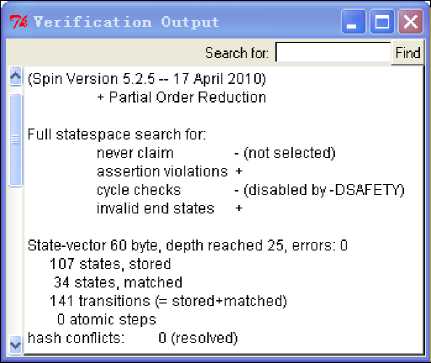
Figure 13. Verification Output.

#define p (LOCK==0) never { /* !(<> p) */ accept_init:

T0_init:

if

:: (! ((p))) -> goto T0_init fi;

}… depth 0: Claim reached state 3 (line 73) (Spin Version 5.2.5 -- 17 April 2010)

+ Partial Order Reduction

Full statespace search for: never claim + assertion violations + (if within scope of claim) acceptance cycles + (fairness disabled)

invalid end states - (disabled by never claim)

State-vector 44 byte, depth reached 0, errors: 0

1 states, stored

0 states, matched

1 transitions (= stored+matched)

0 atomic steps hash conflicts: 0 (resolved)

#endif

Figure 14. Verification result with LTL.

V. conclutions

We have presented our experience in formally verifying system code. The challenges for formal verification at the kernel level relate to performance, size, and the level of abstraction. Since the early attempts at kernel verification there have been dramatic improvements in the power of available tools. Tools like Coq, BLAST and SPIN have been used in a number of successful verifications. This has led to a significant reduction in the cost of formal verification, and a lowering of the feasibility threshold. At the same time the potential benefits have increased.

We take the theorem proving and model-checking as the main technical methods to resolve the key techniques of verifying OS kernel. Theorem proving method is combined with program correctness validation technology based on Hoare logic to establish the axiom semantics of C program. Coq is then used as an interactive theorem proving tool to prove program correctness. Utilizing two model-checkers, a model check approach with a modeling method based on C program and a formal specification method based on LTL to description system attributes has been developed. We have shown that full, rigorous, formal verification is practically achievable for OS kernel code with very reasonable effort compared to traditional development methods.

Acknowledgment

This paper is supported by the National Natural Science Foundation of China under Grant No.60736017.