Cognitive Barriers in Training the Students of Higher Education Institutions, Methodology for Their Elucidation and Overcoming

Published Online February 2013 in MECS DOI: 10.5815/ijmecs.2013.02.01

The analysis of publications related to the topic of cognitive barriers allows one to argue that among the problems of pedagogic science formulated within a principle of developing education, the problem of informative difficulties is likely the most intriguing one. Indeed, the fact that university entrants belong to the category of “trainees” which should be prepared for learning the offered material seems to be obvious. Therefore, the third component of a triad «how to learn, what to learn, how to study» one can consider as playing the subordinated role (if not as strained at all). At least, in relation to two other parts of the above triad, this third component should be of less importance. However the researches, carried out in the eightieth – ninetieth years of the last century have showed that the further improvement of training technique is connected with readiness (ability) of a subject to learn the offered material. Moreover, the researchers came to conclusion that there are regularities of not only understanding of training material, but also regularities of its misunderstanding. As a result, the third component of the triad (how to study)

has allowed one to expand a range of questions, answering which becomes a necessary stage of training process. It is natural that the basic moment in this line is search for general didactic aspects explaining the reasons of cognitive barriers. As to a range of possible barriers which in principle can play an essential role in the training process (at different levels), it, in our opinion, can be expanded in the future.

In current interpretation, the aforementioned triad has been formulated just recently, about fifteen years ago. Meanwhile, the investigations in this direction were started about twenty five – thirty years ago (see [1-3] and the literature cited therein). In particular, it is assumed that key element of this approach is a principle of complementarity introduced in pedagogic science in 1993 (similar to Bore’s complementarity principle used in physics). Finally, in 1997 the concept of cognitive barriers, caused by the third component of the above triad, was formulated. Actually, owing to the works, first of all, by A.A. Pinsky, A.I. Pilipenko, G.G. Granatove, V.A. Popkov, A.V. Korzhuyev, E.V. Shevchenko, a new research direction in pedagogic science was outlined. This direction seems to be very promising from the viewpoint of carrying out the scientific research.

In the course of training, the information can be perceived, or, for any reason, not to be perceived. Besides, it can be incorrectly interpreted or simply distorted during its processing. Therefore, the corresponding negative phenomena in cognitive activity of the student appear quite naturally. These phenomena can be referred as to cognitive barriers , i.e. these are a set of phenomena which affect negatively the cognitive abilities of the student. In reality, a level of intellectual readiness of a student to understand the material studied can be an indicator of such barriers manifestation. Having revealed the specified readiness, one can determine one or another cognitive barrier, with which students face during the training process.

There are four levels of a problem related to the third component of the abovementioned pedagogical triad.

The first level represents types of barriers; the second one is signs of their manifestation; the third level, which we suggest to designate as technological, should include techniques used for cognitive barriers identification. If the first two levels can be considered as adequately stud- ied, the third level is still open for investigations. Finally, the fourth level reflects manifestation of the barriers in real training process. The existence of cognitive barriers just at technological level represents a real challenge that makes such investigations very important (See figure).

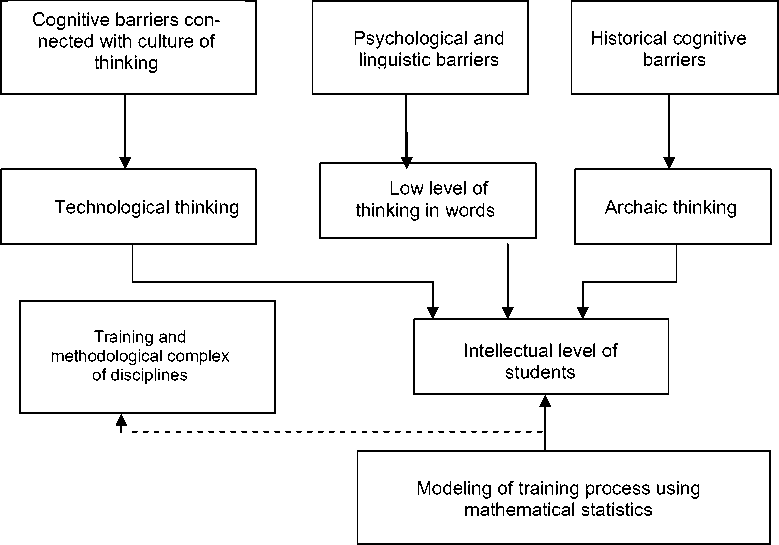
1 – Types of cognitive barriers; 2 – Signs of the barriers manifestation; 3 – Manifestation of cognitive barriers in real training process; 4 – Methods for cognitive barriers revealing

Figure 1. The diagram of cognitive barriers

One can state that by the end of the ninetieth years of the twentieth century, the studies into the problem of cognitive difficulties have shown that organization (planning) of educational process should include some actions aimed at overcoming the barriers mentioned. It is clear that to reach this goal one should have the corresponding methodologies, which by the beginning of our researches published in works [4 -9] have not been developed yet. Thus, a problem of theoretical developments realization has been put into the forefront. It is necessary to emphasize that it is not simply a technical task. Really, it is not so obvious how to apply a problem of cognitive barriers to the real environment, where training process is realized. Such environment is known to have specific features in each higher education institution, in each region, and, at last, in each training group.

The concept of cognitive barriers in education focuses the teacher on intellectual problems of a student. It starts from the assumption that training activity can not be carried out without the purposeful and systematic alerting and overcoming the barriers presented in consciousness of the student. Thus, a characteristic feature of this concept is a strict determination of the elements (in training material), the sense of which can be distorted either by the cognitive barriers functioning in con- sciousness of the student or in the initial text. In other words, the system of formed knowledge, abilities and skills of thinking should be correlated with the system of cognitive barriers and the corresponding mechanisms of educational consciousness. The teacher, when preparing training material or planning lectures, should comprehend probable cogitative problems of students, he should predict a possibility and reveal points of probable mismatch between his own efforts and cognitive efforts of students. From a position of daily pedagogical practice it means that the development of educational and methodical materials for this or that specialty should be preceded by such preliminary work which would take into account all the conditions, the fulfillment of which provides high level of training process. A necessary element of such a work is an elucidation of intellectual ability of students to understand the training material in necessary volume. The problem is in application of certain methodology, which includes a procedure for evaluation of such ability during the organization of training process for specific contingents of students. The main content of the manuscript is organized as follows. First, we discuss the methodology proposed by us for elucidation of cognitive barriers of students. In this line, we rationalize the choice of optimal number of criteria needed to analyze the results of survey made on the basis of specially se lected tests. Then the results obtained are analyzed according to the criteria selected using the methods of mathematical statistics. Finally, the relationship between the criteria mentioned is evaluated using the Chuprov’s mutual contingency coefficients. The evaluation has shown that the criteria have high degree of uniformity. Therefore they can be used for combined analysis to obtained conclusions of general character. It is concluded on specific cognitive barriers inherent in most students studying humanitarian and economic disciplines. In the last section of the manuscript, the methodological recommendations for discipline “Concept of modern natural sciences”, which can be used for overcoming the cognitive barriers, are discussed.

• II.    RESULT AND DISCUSSION

  Our investigations comprise three stages: 1) acquisition of primary information; 2) statistical manipulation of the primary information; 3) analysis of statistical information. The first stage of the research is based on survey method, which employs the test tasks including ten questions. Survey is an indispensable method used to obtain information on the human world, people propensities, motives of activity, opinions. In certain sense, this method is universal: its application allows any information to be obtained. However, one should bear in mind that information obtained with the help of the survey contains subjective opinions and estimations, which are subjected to changes and depends on survey conditions and other circumstances. Therefore, at the second stage of the research the information obtained is statistically processed, i.e. it is systematized and classified according to similarity signs. At the third stage of the research, the information is statistically analyzed using descriptive and mathematical methods. 1417 persons took part in experiment, among them 1191 full-time students and 226 external students.

According to the common knowledge, the success in application of statistical methods for the analysis of experimental results very often depends on two conditions. The first one is the small amount of parameters (criteria), on the basis of which the database (used for further processing) is formed. Secondly, the chosen criteria should most fully correspond to the information, which should be obtained during the statistical manipulations. The analysis of answers of our questionnaire (obtained for three-year cycle), has allowed us to choose the following integrated criteria: 1) school level of knowledge of the interrogated students; 2) desire to study; 3) proneness to study the natural-science and (or) humanitarian disciplines; 4) interest to a subject. The analysis carried out on the basis of the specified criteria allowed eventually to elucidate the cognitive barriers (difficulties), which the students face with during studying the mathematical and natural-science disciplines, including the course «The concept of modern natural sciences» (CNS). The latter is a complex discipline. Its studying is based on knowledge of a certain volume of a specific material from several natural-science disciplines (first of all, of course, physics). From here follows the problem causing difficulties (barriers) in studying this specified subject. We mean here the readiness of student studying CNS to comprehend (to generalize) fundamental knowledge, on which the modern representations underlying a naturalscience picture of the world, are based. The results of the statistical analysis given below reflect the results of the investigations carried out by us in this line.

• A. Assessment of School Level of Knowledge

There were assessed answers to a question: “What marks did you have at school on natural-science disciplines?” Then information obtained was statistically analyzed. The results of the analysis are given in Table I. The analysis was carried out on the basis of existing methods of database processing [10, 11]. It is pertinent to note here that students could give not absolutely exact information concerning their marks at school. This fact indicates the necessary quantitative processing of the survey results that will allow one to make adequate conclusions.

We mean here the application of statistical methods, which allow to do general (predictive) conclusions on the basis of small actual material. Our methodology assumes the initial determination of sample average ( x ) of the corresponding parameter and mean square devia- 2

tion ( σ ) separately for each group. The values x and σ allow also to assess the degree of uniformity of the marks analyzed on the basis of variation coefficient (V ) and mode factor (M ).

Here it is necessary to make the following explanations. Uniformity is a property which shows proximity of characteristics belonging to the separate phenomena which form the given set. For an assessment of uniformity, the variation coefficient ( V ) is used. The latter is equal to the relation of mean square deviation to sample average. If variation coefficient is less than 33 %, the given set is uniform. In uniform set, the values of indicators are typical (i.e. they are close). Naturally, that in non-uniform set (variation coefficient >33 %), values of indicators are non-typical (i.e. opposite). Thus, determination of uniformity is necessary to find out whether the opinions of students concerning this or that question coincide. Evidently, the set of students is diverse from the viewpoint of social, biological, family, economic and other reasons, but it is qualitatively uniform with respect to training process aimed at the preparation of high-skilled professionals.

The parameters used by us for statistical processing of experimental data have been calculated using the following equations [11].

TABLE I. ASSESSMENT OF SCHOOL LEVEL OF KNOWLEDGE

Year Training Interval Interval x Number of students f xf xm E И И и6 и 1 2 3 4 5 6 7 8 9 8 s 3 b 2,3,4,5 3,5 - - 4,2 - - 3,4 3,5 25 87,5 0,7 12,3 3,4,5 4 52 208 0,2 2,1 4,5 4,5 86 387 0,3 7,7 5 5 12 60 0,8 7,7 Total 175 742,5 2,0 29,8 1 * Щ 2,3,4,5 3,5 - - 3,9 - - 3,4 3,5 32 112 0,4 5,1 3,4,5 4 14 56 0,1 0,1 4,5 4,5 13 58,5 0,6 4,7 5 5 3 15 1,1 3,6 Total 62 241,5 2,2 13,5 8 8 S "3 2,3,4,5 3,5 1 3,5 4,2 0,7 0,5 3,4 3,5 39 136,5 0,7 19,1 3,4,5 4 61 244 0,2 2,4 4,5 4,5 120 540 0,3 10,8 5 5 18 90 0,8 11,5 Total 239 1014 2,7 44,3 3 8 Щ 2,3,4,5 3,5 - - 4,0 - - 3,4 3,5 15 52,5 0,5 3,8 3,4,5 4 9 36 0,0 0,0 4,5 4,5 10 45 0,5 2,5 5 5 1 5 1,0 1,0 Total 35 138,5 3,2 7,3 о 8 8 3 b 2,3,4,5 3,5 2 7 4,2 0,7 1,0 3,4 3,5 42 147 0,7 20,6 3,4,5 4 53 212 0,2 2,1 4,5 4,5 114 513 0,3 10,3 5 5 17 85 0,8 10,9 Total 228 964 2,7 44,9 3 8 X Ш 2,3,4,5 3,5 2 7 3,9 0,4 0,3 3,4 3,5 34 119 0,4 5,4 3,4,5 4 92 368 0,1 0,9 5 5 1 5 1,1 1,2 Total 129 499 2,0 7,8 xm

S xfL f

стг

L ⁽ x - x m ) 2 ^f

S f

V = CT

V  x m

M = Xm + /

^f^M - 1 )

M

—

f ( M + 1 )^]

• f - frequency of modal interval;

• f )m fre — frequency of pre-modal interval;

• f (m+i) — frequency of post-modal interval;

i – value of modal interval.

It is rational to calculate a mode, when the studied set contains some amount of units with very high or very low value of the varying sign. These values of variants (not typical for the whole set) influencing an arithmetic mean, determine values of modes in essentially smaller degree that makes the latter valuable indicators for statistical analysis. Table II shows initial data for modes calculations.

Where, X - lower bound of modal interval;

TABLE II. INITIAL DATA FOR MODES CALCULATION

	2003 - 2004		2004 - 2005		2005 - 2006
	Full-time	External	Full-time	External	Full-time	External
fM	163	59	220	34	209	126
fM - 1	0	0	1	0	2	2
fM + 1	12	3	18	1	17	1
xM	3	3	3	3	3	3
i M	2	2	2	2	2	2

TABLE III. CALCULATED CHARACTERISTICS OF DATA

Training	7 2	7	V , %	M
Full-time 2003-2004	0,17	0,41	9,8	4,04
External 2003-2004	0,22	0,47	12,1	4,03
Full-time 2004-2005	0,19	0,44	10,5	4,04
External 2004-2005	0,21	0,46	11,5	4,01
Full-time 2005-2006	0,20	0,45	10,7	4,04
External 2005-2006	0,06	0,24	6,2	4,00

TABLE IV. DESIRE FOR ADVANCED STUDY: ANSWERS TO QUESTIONNAIRE

Education	Variants of answers	Academic year
		2003 - 2004		2004 - 2005		2005 - 2006
		Number of answers	Percentage	Number of answers	Percentage	Number of answers	Percentage
Full-time ОЧНОЕ	No	31	17,7	62	26,0	46	20,2
	Difficult to answer	54	30,9	-	-	24	10,5
	Do not know	12	6,8	13	5,4	20	8,8
	Yes	78	44,6	164	68,6	138	60,5
	Total	175	100	239	100	228	100
External	No	10	16,1	5	14,3	16	12,4
	Difficult to answer	30	48,4	-	-	44	34,1
	Do not know	13	21,0	-	-	1	0,8
	Yes	9	14,5	30	85,7	68	52,7
	Total	62	100	35	100	129	100

TABLE V. PREFERENCES OF STUDENTS IN STUDYING THE SUBJECTS: ANSWERS TO QUESTIONS

Education	Preferred subjects	Academician year
		2003 – 2004	2004 – 2005	2005 - 2006
		Number of answers	Number of answers	Number of answers
Full-time	Humanitarian	18	23	6
	Natural science	157	216	222
	Total	175	239	228
External	Humanitarian	9	3	21
	Natural science	53	32	108
	Total	62	35	129

Frequency of modal interval in our case corresponds to a number of students included in calculation. According to the above remark on reasonability of application of median as the mean characteristic of the data for assessment of f value, have not taken into consideration the intervals of answers 2, 3, 4, 5 and 5 with low (or even zero) f value. Naturally therefore that x M ³ and i M ² .

The calculated M values are summarized in Table III, in which 7 ² , СТ , V parameters are also given. This data evidence that the analyzed experimental data are uniform, and the majority of students participating in survey had on the average good marks in natural-science disciplines at school.

• B .    Desire to Study

At first glance, one can seem that this parameter is farfetched: after all, if the student has entered the university, it means that he wants to study. However, our survey has shown that quite often the student does not learn those disciplines, which he would like to learn. There are two reasons for this fact: 1) high competition (as a rule, it relates to free-of-charge education) makes it impossible to enter the university for all school-leavers; 2) sometimes, future profession is chosen not by students themselves, but their parents (especially it is typical for charged education).

As a result, it becomes clear that students do not aspire to deep studying the necessary (according to academic curriculum) subjects. However, they show an interest in subjects from other fields of knowledge.

To define, whether students want to acquire novel knowledge, we have asked them a question: "Would you like to study any subject deeply?" We mean here the

subjects of natural-science disciplines. The answers given by the students, shows that about sixty percent of full-time students and fifty percent of external students express a desire for advanced study (Table IV). It should be emphasized that considerable group of the interrogated students was indifferent concerning this question.

• C.    Preferences of Students in Studying the Naturalscience and (or) Humanitarian Disciplines

The third criterion which we have used to solve the problem of the cognitive difficulties is the preferences of students relative to one or another subject.

We suppose that this criterion is important, because the success in learning the ideas of a natural-science picture of the world at level of the requirements defined by academic curricula of higher education institution depends substantially on the possibility to study naturalscience disciplines. Certainly, the above preference itself, if to use the accurate mathematical definition, is not yet sufficient condition for the successful study. Eventually, the student is obliged (whether he can or wants this or not) to study the disciplines provided by the academic curriculum. Nevertheless, these data also increase adequacy degree of entrants knowledge, which need for learning the high school program, i.e., finally, for becoming the high-skilled expert. Naturally, the teacher who begins to work with these students, has additional information which (at least, in principle) allows the educational process to be organized more effectively.

Before our survey, we have divided subjects into two groups: humanitarian and natural-science ones. Certainly, in this division there is a certain element of conditionality. Therefore we gave the explanation to students concerning the meaning of this division.

Of course, we bear in mind the fact that there will be also such students who show interest in subjects of the both groups. Results of the survey have shown that the students obviously prefer natural-science subjects (a ratio of answers 595/47 for full-time and 193/33 for external students).

• D.    Interest to a Subject

To gain a better understanding of the students’ readiness to learn CMS, we asked the students why they liked this or that subject (which, in this case, is not essentially) at school (Table VI).

In our opinion, answers to similar questions also promote (though indirectly) to more adequate idea on potential possibilities of student, which should the teacher work with. Starting the survey, we have asked the students to specify the reason of their interest in the studying this or that subject at school. Among such reasons are the following ones: the personal interest in a subject, intriguing teaching, understandable subjects. However, there were students who found it difficult to answer something to this question. Thus, if to judge according to the answers received by us to the above question, the majority of the interrogated students can be considered as trained enough for higher education institution. At the same time, the essential percent of respondents (39 % and 43 % for full-time and external form of education, respectively), which gave no any answer, can testify to the inert relation of these students to educational process at school.

• E.    Evaluation of Correlation Using Chuprov’s Coefficient

According to the current knowledge, the statistical analysis of the databank is carried out with the purpose of formation of a model which could describe quite adequately the studied phenomena and (or) processes, which the analyzed databank belongs to. In the case when several signs (factors) are used for this purpose, it is necessary to evaluate their correlation using Pearson or Chuprov mutual contingency coefficient [11]. Primary or initial statistical information necessary for the quantitative analysis of correlation between factors used during the modeling is put into the tables similar to Table VII.

table vi. T he interest of student in learing subjects: A nswers to questions

Education	Reason of interest	Academician year
		2003-2004	2004-2005	2005-2006
s	The subject is interesting	48	71	65
	Ardor	29	49	32
	Good teachers	13	19	21
	The subject is understandable	14	14	18
	Difficult to answer	71	86	92
	Total	175	239	228
1 Щ	The subject is interesting	9	14	30
	Ardor	7	6	29
	Good teachers	7	5	6
	Difficult to answer	2	3	10
	Difficult to answer	37	7	54
	Total	62	35	129

TABLE VII. TABLE OF INITIAL DATA FOR CALCULATION OF MUTUAL CONTINGENCE COEFICIENTS

Factors	A	B	C	Total ny
D	f 11	f 12	f 13	A 1 i
E	f 21	f 22	f 23	A 2 i
F	f 31	f 32	f 33	A 3 i
Total ( nx )	A 1 j	A 2 j j	A 3 j	n

Where f ^ — frequencies of mutual contingency of two attributive factors; П — total number of paired observations.

Pearson’s coefficients ( C ) are calculated by the formula

K =

C =

ф111 1+ф1

where ф — is an index of mean square contingency. It is defined as sum of relation of square frequencies of each column of the Table to the product of total frequencies of the corresponding column and line minus 1:

ф1

x

2 f j

A A i j J

— 1

where f — is a frequency of each column, i — line

number, A_f — total frequencies of lines, Aj — total

frequencies of columns, j — column number.

It is a common knowledge that in investigations similar to ours, it is preferable to apply Chuprov’s coefficients ( K ) which are calculated as follows:

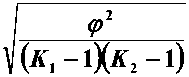
where ф is the same factor as given in expression (6), K — is a number of groups in table columns, K ₂ — is a number of groups in table lines.

Factors C and K change within limits from zero to unit. Distinct from zero value testifies to the existence of correlation between the factors. The higher value of C and (or) K corresponds to deeper correlation between these factors [11].

To elucidate the correlations between four factors used by us, we have performed the corresponding analysis. Below are given Chuprov’s coefficients calculated by comparison of two factors: assessment of school level of knowledge and desire to study. Initial data for these calculations, taken from Tables I and IV, are summarized in Table VIII (separately for every year). Both considered factors turn to be alternative, i.e. the students can either possess them or not possess. In such cases, the presence of a factor is designated by 1, and its absence by 0.

TABLE VIII. TABLE OF INITIAL DATA FOR CALCULATION OF CHUPROVE COEFFICIENTES

Academic year	Education	Desire to study	Assessment of school level of knowledge (variants of answers) f					Total
			2,3,4.5	3,4	3,4,5	4,5	5
20032004	Full-time	No	-	7	4	19	1	31
		Do not know	-	6	17	4	1	28
		Yes	-	12	31	63	10	116
		Total	-	25	52	86	12	175
	External	No	-	4	3	3	-	10
		Do not know	-	18	3	2	2	25
		Yes	-	10	8	8	1	27
		Total	-	32	14	13	3	62
20042005	Full-time	No	-	19	14	25	4	62
		Do not know	1	1	4	7	-	13
		Yes	-	19	43	88	14	164
		Total	1	39	61	120	18	239
	External	No	-	4	1	-	-	5
		Do not know	-	-	-	-	-	-
		Yes	-	11	8	10	1	30
		Total	-	15	9	10	1	35
20052006	Full-time	No	-	10	10	22	4	46
		Do not know	1	10	16	12	5	44
		Yes	1	22	27	80	8	138
		Total	2	42	53	114	17	228
	External	No	1	4	6	5	-	16
		Do not know	-	13	19	13	-	45
		Yes	1	17	20	29	1	68
		Total	2	34	45	47	1	129

The paired observations n (Table IX) have been performed on the basis of data given in Table VIII. The data of Table IX are obtained by summing of the corresponding frequencies for every year (separately for full-time and external students. Thus, values f from column "2, 3, 4, 5", which are significantly lower than the similar values from other columns, are not taken into considera- tion. The data of Table IX are used as initial data for the calculation of mean square contingency coefficient ф and Chuprov’s correlation coefficient K the compared factors (school level of knowledge and desire to study) using expressions (6) and (7). Below is given an example of such calculation.

\   36 2        17 2        53 2         28 2        39 2        102 2        66 2

111111+

( 106 • 139  106 • 85  106 • 418  169 • 139  169 • 85  169 • 418  320 • 139

32 2   )

+-----+------+-----+----+-----

320 • 85  320 • 418  47 • 139  47 • 85  47 • 418 )

- 1 = 0 , 06

^K Full =

0 , 06

V J (4 -* -1)

= 0 , 15

f 12 2      31²      38²      11²     23 2       36²       8²

111111+

( 81 • 31  81 • 71  81 • 124  70 • 31  70 • 71  70 • 124  70 • 31

+----+-----+---+----

70 • 71  70 • 124  5 • 71  5 • 124 )

- 1 = 0 , 03

K Ext =

0 , 03

V J (4 - 1)(3 - 1)

= 0 , 11

The paired comparison of other factors constitutes the next step in elucidation of the correlation. It is pertinent to note once again that we operate here with of criteria of the integrated character used by us for the identification of the cognitive barriers (difficulties), which the students face during the studying of mathematical and natural-science disciplines, including CNS. As in the case of comparison of factors «school level of knowledge» and “desire to study”, we start here from the selection of the corresponding paired values (obtained from the answers of the survey) per every year separate- ly (similar to those given in Table VIII). These data were collected in Table (analog of Table IX) containing total values of frequencies f for three years separately for full-time and external students. Then the mean square contingency ϕ2 and Chuprov K coefficients are between the factors compared are calculated using the expressions (6) and (7). The coefficients found characterizing the correlations between various factors are shown in Table X.

TABLE IX. SUMMARY OF PAIRED OBSERVATION

Academic year	Education	Desire to learn	School level of knowledge f				Total n y
			3,4	3,4,5	4,5	5
о s	Full-time	No	36	28	66	9	139
		Do not know	17	39	23	6	85
		Yes	53	102	231	32	418
		Total n	106	169	320	47	642
	External	No	12	11	8	-	31
		Do not know	31	23	15	2	71
		Yes	38	36	47	3	124
		Total n	81	70	70	5	226

The data given in Table X unequivocally evidence that the experimental data analyzed (answers to the questions) possess high degree of uniformity. In its turn, it means that the criteria of integrated character offered by us (school level of knowledge, desire to study, inclination to natural-science and (or) humanitarian disciplines, interest in a subject) – can be used for the combined analysis allowing the general conclusions to be made.

From a position of the cognitive barriers theory, the experimental data obtained should be considered as indicators of availability of cognitive barriers in students caused by technological style of thinking, i.e. receptor thinking, which hinders the development of a deeper productive thinking. In this case, even well acquired system of knowledge and skills is perceived by students as a game in correct answers to correct questions. But "correct" question formulated in unusual form will stand a student in helpless situation.

TABLE X. SUMMARY OF CHUPROV’S COEFFICIENTS

Education	Comparable factors
	Level of knowledge/D esire to study	Level of knowledge / Inclination to subject	Level of knowledge / Interest in subject	Desire to study / Inclination to subject	Desire to study / Interest in subject	Inclination to subject / Interest in subject
Full-time	0,15	0,17	0,14	0,20	0,19	0,25
External	0,11	0,11	0,17	0,20	0,15	0,35

The performed analysis of the data indicates the existence of cognitive barriers of historical type in the entrants. From the methodological viewpoint, these results make prerequisites for the application of historical aspect of science development for optimization of educational process.

On the basis of the conclusions on cognitive barriers in students of higher education institutions, the training and methodological recommendations (TMR) related to CNS discipline have been worked out. These recommendations are aimed at overcoming these barriers. This discipline is based on a course of lectures on foundations of physics formulated by the moment in most conceptual form. The results of checking the residual knowledge in the students studying CNS according the TMR can serve as the proof of efficiency of our methodology for elucidation and overcoming the cognitive barriers. Students from thirty seven groups were tested, histograms of density distribution of pedagogical evaluations were made, and coefficients maps of tasks solution for the period 2005-2010 were compiled. Comprehensibility of all training material was 70 %. This is rather high average value.

• III. CONCLUSION

In conclusion, one can make the following remarks.

• 1.    The investigations carried out in the nineties of the twentieth century have shown that there are regularities of not only understanding of training material, but also regularities of its misunderstanding (a principle of Bore complementarity in pedagogic science). From this follows the corresponding negative phenomena in educational cognitive activity of the students which can be referred to as cognitive barriers. These are the distorted incorrect knowledge and notions of students, which hamper obtaining new ideas on the world and hinder self-realization of the student.

• 2.    The methodology for identification of cognitive barriers in students has been proposed and developed. Its realization involves three consecutive stages. The first stage of the investigation comprises the survey on the basis of test tasks. At the second stage of the investigation the information obtained is systematized and grouped according to main factors of similarity. At the third stage, the experimental data are processed using methods of mathematical statistics by an assessment of correlation between factors of similarity. For this purpose Chuprov’s coefficients of mutual contingency are applied. It is shown that our criteria and indicators really characterize cognitive barriers of students. The efficiency of our methodology has been demonstrated for identification of the most typical cognitive barriers inherent of school-leavers entering at higher education institutions of humanitarian and economic profiles.

• 3.    Specific methodological recommendations for the discipline «The concept of modern natural sciences» for the students of economic and humanitarian profiles of higher educational institutions has been worked out. This discipline is based on a course of lectures on foundations of physics formulated by the moment in most conceptual form.

• 4.    In our opinion, the promising directions of further research can be the search for general principles which should constitute the basis for specific methodological developments accounting for the cognitive barriers of the students. In real practice, an intellectual ability of the student to comprehend the training material is an indicator of such barriers manifestation. Having revealed the specified ability, one can assume the availability of these cognitive barriers which the students face with during the training.

A circle of possible cognitive barriers related to the third component of pedagogical triad «how to learn, what to learn and how to study», which can play an essential role in educational process, can be expanded in the future.