Collaborative Anti-jamming in Cognitive Radio Networks Using Minimax-Q Learning

Cognitive radio (CR) concept was proposed in [1] to resolve the problem of spectrum scarcity by exploiting the spectrum holes by the secondary users (SUs). The cognitive radio network (CRN) as proposed in [1] and [2] solves the conflicting situation between limited spectrum utilization and the increasing demand for spectrum resources. It exploits the spectrum holes by enabling the SUs to sense, select the free channel, collaborate with the other SUs, access the free channels and free the channels whenever the primary user (PU) needs those channels. Main research concerns till now were spectrum sensing, sharing and accessing procedures.

These works have assumed that SUs are greedy for spectrum holes and cooperate among themselves to fulfil their common objective. This assumption ignores the jammer’s attack on SU scenario. In order to provide secure spectrum sharing in CRN, the random jammer’s attack has to considered and modelled. Markov Decision Process (MDP) in CRN was introduced in [3] as it can easily model the competitive behaviour of SUs in the limited spectrum scenario of CRN. Stochastic games in CRN, is given in [4], [5] and [6], where a game was designed between the jammers and the SUs and zerosum game condition also fetched the games’ boundary conditions. The same framework is extended for MDP in [7] and [8], where competitive interaction among agents was considered in detail. In [8] and [9] MDP is used for the reinforcement learning (RL), this RL technique make the SUs learn the policies adopted by jammer. So, after learning the jammers’ policy the SUs can predict jammer next action and plan their next course of action to combat the jammers. The reinforcement learning concept as introduced in (RL) [10], [11] and [12] has been used in the anti-jamming scenario, was introduced in [13] and [14]. Jammers attack in CRN can be modelled as zerosum stochastic game framework. A zero-sum antijamming game is developed in [15] and the extension of QV learning is covered in [16] and [12]. One more advanced and online reinforcement algorithm is Minimax-Q learning is coined in [17] where there is an improvement in the learning probability of the SUs can be achieved as compared with the simple QV reinforcement learning algorithm. In the framework as developed in [15] quality of channel, availability of spectrum and the observation of attackers’ actions define the state of game. The SU’s actions, jammer’s actions PU presence or absence, channels utilization gains and switching between jammed and un-jammed channels are modelled. This work has considered the SUs as independent agents learning independently without any collaboration with the other SUs. An improvement in the learning probability can be achieved by using the collaboration concept given in [18] and [19]. Here, collaboration is achieved via sharing the learned policies or episodes. In this paper, we propose the collaborative multi-agent multi-band anti-jamming game that involves the sharing of the local statistics, i.e., the number of jammed data or control channels or the number of unjammed data or control channels. To achieve the collaboration, this information is shared in the CRN with the neighbouring agents. The independent SUs will use the same decision policy by using Minimax-Q learning algorithm. In the proposed game each agent updates the Q-matrix for the same policy independently but now the rate of update gets multiplied by the number of collaborating SUs simultaneously. This sharing of the learned policies or episodes enhances the learning probability of SUs about the jammer’s strategies.

This paper is organized as follows. In section II, we have covered the system model along with the basic assumptions involved. In section III, we have given the Minimax-Q learning algorithm and collaborative multiagent multi-band anti-jamming game that involves the sharing of the local statistics, i.e., the number of jammed data or control channels or the number of un-jammed data or control channels. In section IV, we have presented the simulation results and in section V conclusion is given.

• II.    SYSTEM MODEL

In this section, we give all the assumptions and notations for the given stochastic game model in brief. Further details of the game scenario are given in [15]. We assume that all the SUs are under the control of a single secondary base station and the jammer can only jam the SUs. Moreover, the jammer can jam at most N channels in each time slot due to limited number of antenna channels and transmit power. Here, the dynamics of channel, PU’s presence or absence, SUs actions and channel utilization gain has been modelled as in [15] and we have used the same developed system model. The basic analytical expressions involved are as follows [15]. The SUs’ motto is to get an optimal policy with maximum expected summation of discounted reward max[ E [X Yr (s', a', at)]]                   (1)

t = 0

In the anti-jamming stochastic game the value of state V (st) is given by

V ( ^s ) = max min X Q ( ^s , a , ^a_:) ⁿ (a )     ⁽²⁾

n (a ) nj (aj ) at £ A where, Q(s , a , a j) stands for the Q-value of state and is updated by

Q (st, at, a') = r (st, at, a') + t+i

/ x X P ( s t ⁺ 1 1 s t , a t , a j ) X V ( s t ^{+ 1})

s

To reduce the complexity, equation for updating the Q-function has been modified as

Q ( s t , a t , a t ) = (1 - a ) x Q ( s t , a t , a t ) jj

+ ( a ' ) x [ r ( s t , a t , a ' ) + у x V ( s t ^{+ 1})]

αt stands for the learning rate decays for the time by

α^t+1 = µα^t with 0 < µ< 1. The action set a^t={a^t 1 ,a^t 2 ,...,a^t L }. The actions of the jammer are formulated as a^t J ={a^t 1,J , a^t 2,J ,...,a^t L,J }. The states of the anti-jamming game at time t is defined as s^t ={s^t ₁ , s^t ₂ ,…, s^t _L } and s _l ^t={P _l ^t, g _l ^t, J _l,C ^t, J l,D ^t }. The transition probability is expressed

L

P ( s t ^{+ 1} | s t , a t , a* j ) = П P ( s l ^{+ 1} | s l , a l , a! j )     ⁽⁵⁾

l = 1

The transition probability p(s l^t+1 | s l^t , a l^t , a l^tJ ) can also be expressed as

„'+1 I jt jt jt \ rt+1 rt+1 I jt jt jt „ t p ( s | s , a , a J ) = p(Ji, C , Ji, D | Ji, C, Ji, D, ai , aij ,) X ,   ,    ,,           (6)

p ( P ^{+ 1} , PPVP , g tt )

The cumulative average reward per iteration as given by the equation t'

rt = 1/ t{ X r ( s t , a t , a j )}                       (7)

t = 1

a^t l = (a^t l , C1 , a^t l , D1 , a^t l , C2 , a^t l , C2 ) where action a^t l , C1

(or a^t l , _D1 ) stands for the fact the secondary network will transmit control (or data) messages in a^t l , C1 (or a^t l , D1 ) channels by uniformly selecting from the earlier unjammed channels, and action a^t l , C2 (or a^t l , D2 ) means that the secondary network will transmit control (or data) messages in a^t l ,_C2 (or a^t l ,_C2 ) channels uniformly selected from the previously jammed channels with(a^t l , _J1 ) or (a^t l , _J2 ) means that the attackers will jam (a^t l , J1 )or (a^t l , J2 ) channels uniformly selected from the previously un-attacked (or attacked) channels at current time t. Detailed mathematical formulation is given in [15].

Minimax-Q learning algorithm for the single independent SU combatting the jammer as given in [15].

• 1)    STEP 1

At state s^t, t = 0,1, …

– if state s^t has not been observed previously, add s^t to s hist ,

– generate action set A(s^t) , and A J (s^t) of the attackers;

• -    initialize Q ( s , a* , a j ^ 1, for all a 8 A(s t ), a J 8 A J (s^t)

• -    initialize V (s) ^ 1;

• -    initialize n (s, a¹) ^ 1/\A(s*)\ , for all a 8 A(s * ) ; otherwise, use previously generated A(s^t) , A_J (s^t) ,

Q ( s^t , a^t , a^t_j ), V (s^t) , and π (s^t);

• 2)    STEP 2 Choose an action at a ^t time t :

• – with probability p exp , return an action uniformly at random;

  – otherwise, return action a^t with probability π (s^t, a) under current state s^t.

• 3)    STEP 3 Learn:

Assume the attackers take action a^t J , after receiving reward r ( s^t , a^t , a^t_j ) for moving from state s^t to s^t+1 by taking action a^t

– Update Q-function Q ( s^t , a^t , a^t_j ) according to (3:9);

– Update the optimal strategy π* (st,a) by n (s*) ^ argmax ,,.min У n (s*, a^Q (s*, a1, a*) n (s*)        n(s*) Z—la                                  j'

• ^— Update V (s) ^ min s * ^^ n * ( s * , a ) Q ( s * , a * , a j ) ^; -Update a^t+1 ^ a t *ц;

• – Go to step 1 until converge.

where, π (s^t ) denotes state policy, r ( s^t , a^t , a^t )is reward of the game. A(s^t) and A J (s^t) denote SU’s and jammer’s actions set.

• A. Collaborative Anti-jamming Game

This framework has been used with the collaborative learning where SUs communicate with each other to combat the jammer. The collaboration can be achieved by the three approaches via sharing the test statistics or sensation, via sharing the iterative episodes or via sharing the learned optimal policy. The additional statistics shared by the agents are useful when used efficiently to speed up the learning, sharing of the learned optimal policy can be judicial, but this improvement is at the cost of the communication. Here, the collaboration has been achieved by sharing the learned optimal policy. Although these joint tasks slow the learning process initially, but it outperforms the independent agents. The proposed multi-agent multiband collaborative anti-jamming game in which each SU uses the single user Minimax-Q reinforcement learning algorithm and same decision policy. Although each SU updates same policy independently, the rate of updating the policy is multiplied by the number of SUs collaborating. It involves the sharing of the local statistics, i.e., the number of jammed data or control channels or the number of un-jammed data or control channels. This information is shared in the CRN with the neighbouring agents for the collaboration. Each agent updates the Q-matrix for the same policy independently but the rate of updating the Q-matrix gets multiplied by the number of collaborating agents simultaneously. Agents performing same task can differ as the exploration of the state space differs. In this way they complement each other, i.e., policy learnt by one can be beneficial for other. It is an independent decision process. This collaborative game between the jammer and the SUs are as depicted. In Fig. 1 Single SU game without collaboration is clearly illustrated. In Fig. 2 two SUs game with collaboration between two agents is shown. Finally, in Fig. 3 three SUs game with collaboration between three agents.

Fig. 1 Single SU game without collaboration

Fig. 2 Two SUs game with collaboration between two agents

Fig. 3 Three SUs game with collaboration between three agents

• IV.    SIMULATION RESULTS

Now, we give the simulation results to evaluate the performance of the proposed collaborative anti-jamming strategy of the SU.

• A.    Anti-jamming for single licensed band

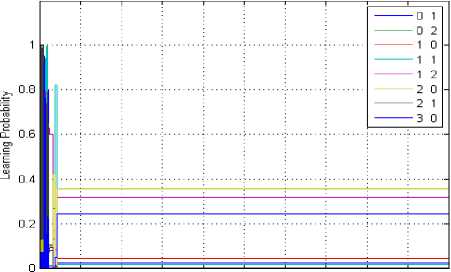
Here, one licensed band is available to the SU, i.e, L = 1 and the other simulation parameters are taken from [15]. Fig. 4 depicts the learning probability of the jammer for no collaboration condition in the state (0, 1, 0, 2). The learning probability is about 0.35 and the number of iterations required to learn are about 430. The different coloured curves show the different strategies of the jammer. Here, the jammer has eight different strategies as listed in the Fig. 4. Out of these eight strategies (2, 0) is having the highest learning probability.

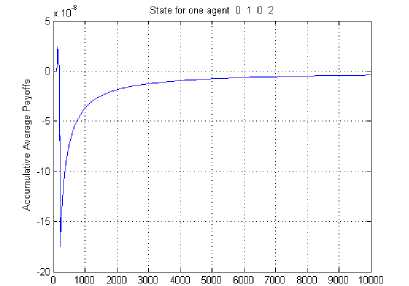
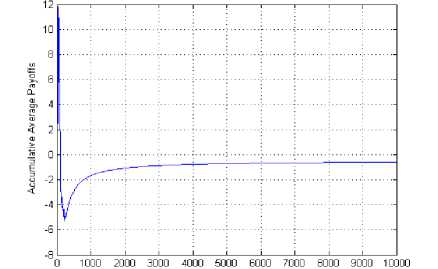
In Fig. 5 the learning probability of single SU is shown for the state (0, 1, 0, 2) for no collaboration scenario. The learning probability of SU is 0.5 and the number of iterations required to learn the jammer’s policy are 430. The different coloured curves show the different strategies of the SU. Here, the SU has 52 different strategies so cannot be listed in the Fig. 5. Strategy (0, 3, 2, 0) is having the highest learning probability. Fig. 6 depicts the cumulative average reward curve of SU for the state (0, 1, 0, 2) for no collaboration scenario. This reward is highest of all three scenario considered because reward decreases as the cost of communication required for the collaborative anti-jamming game increases. Fig. 7 shows the learning probability of the jammer, where two SUs are collaborating for the state (0, 1, 0, 2). The learning probability is about 0.2 and the number of iterations required to learn are about 350.

State of Jammer for one-agent 0 1 0 2

О 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 Iterations

Fig. 4 Learning probability curve for jammer of the state (0,1,0,2), single SU, no collaboration, L=1

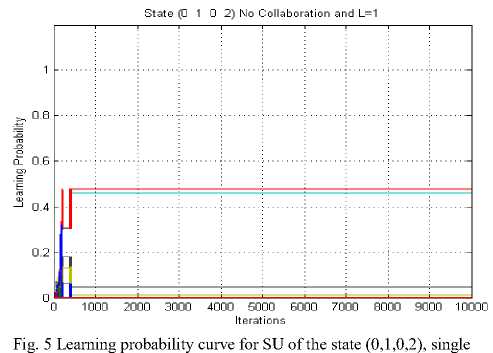
SU, no collaboration, L=1

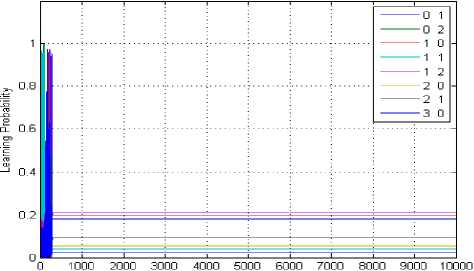
is less than the no collaboration case and more than the three SUs collaborating scenario considered. Fig. 10 depicts the learning probability of the jammer, where three SUs are collaborating for the state (0, 1, 0, 2). The learning probability is about 0.33 and the number of iterations required to learn are about 430. Out of the eight strategies of SU (1, 1) is having the highest learning probability. In Fig. 11 the learning probability of the SUs is shown for the state (0, 1, 0, 2).

Iterations

Fig. 6 Cumulative average reward curve for SU for the state (0,1 ,0, 2), single SU, no collaboration, L=1

State of Jammer for two agentsO 10 2

Iterations

Fig. 7 Learning probability curve for jammer of the state (0, 1, 0, 2), two SUs collaborating, L=1

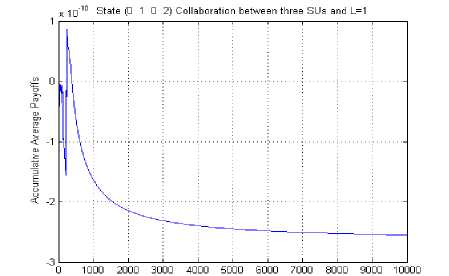
The learning probability is 0.99 and the number of iterations required to learn the jammer’s policy are 200. Out of the 52 strategies of the SU (0, 4, 2, 0) is having the highest learning probability. Fig. 12 depicts the cumulative average reward curve for SU for the state (0, 1, 0, 2) where three SUs are collaborating. This reward is the smallest of the three scenario considered. So, more the number of agents collaborating more the cost of communication and lesser is the cumulative average reward.

Out of eight strategies of the jammer (1, 2) is having the highest learning probability. In Fig. 8 the learning probability of the SUs is shown for the state (0, 1, 0, 2), where two SUs are collaborating. The learning probability is 0.96 and the number of iterations required to learn the jammer’s policy are 340. Out of the 52 strategies of SU (0, 1, 2, 0) is having the highest learning probability. Fig. 9 depicts the cumulative average reward curve for SU for the state (0, 1, 0, 2) where the collaboration between two SUs is employed. The reward

0--'   ' —=—     —=— '    —=——1

□   1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

Iterations

Fig. 8 Learning probability curve for SU of the state (0, 1, 0, 2), two SUs collaborating, L=1

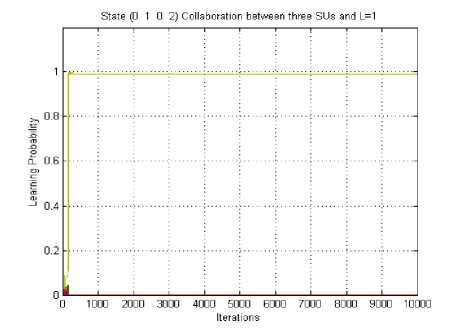
Fig. 11 Learning probability curve for SU of the state (0, 1, 0, 2), three SUs collaborating, L=1

Iterations

Fig. 9 Cumulative average reward curve for SU for the state (0, 1, 0, 2), two SUs collaborating, L=1

Iterations

Fig. 12 Cumulative average reward curve for SU for the state (0, 1, 0, 2), three SUs collaborating, L=1

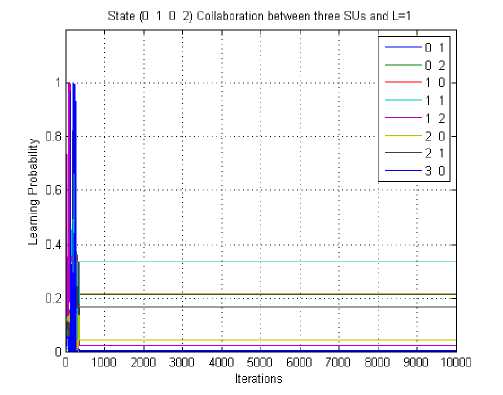
Fig. 10 Learning probability curve for jammer of the state (0, 1, 0, 2), three SUs collaborating, L=1

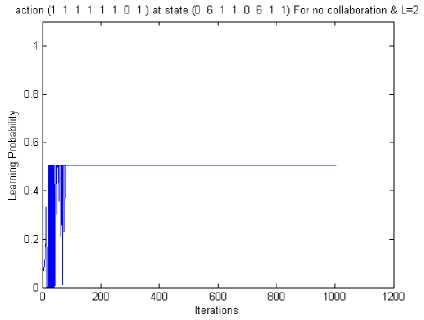
Fig. 13 Learning probability curve for SU of the state (0, 6, 1, 1 ,0 ,6 ,1, 1), single SU, no collaboration, L=2

• B.    Anti-jamming for two licensed band

Here, L = 2 and other parameters are taken from [15]. Fig. 13 the learning probability of single SU is shown for the state (0, 6, 1, 1, 0, 6, 1, 1) for no collaboration case. The learning probability is 0.5 and the number of iterations required to learn the jammer’s policy are 100. Fig. 14 and Fig. 16 shows the cumulative average reward curve of SU for the, state (0, 6, 1, 1, 0, 6, 1, 1), for no collaboration and three SUs collaborating scenario respectively. The reward for no collaboration is more as compared to the collaboration case as the cost of communication required for the collaborative antijamming game is more. In Fig. 15 the learning probability of the SUs is shown for the state (0, 6, 1, 1, 0, 6, 1, 1), where three SUs, are collaborating. The learning probability of the SUs is 0.97 and the number of iterations required to learn the jammer’s strategies are about 80.

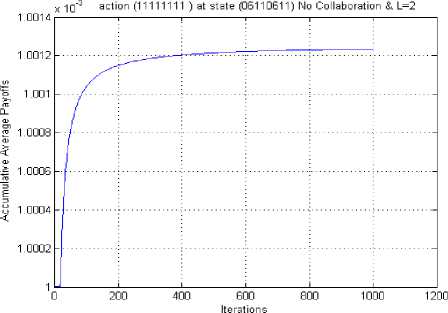
Fig. 14 Cumulative average reward curve for SU for the state(0, 6, 1, 1, 0, 6, 1, 1), single SU, no collaboration, L=2.

Fig. 17 depicts the consolidated view of multi-agent scenario for the multi-band collaborative anti-jamming game so that a clear comparison can be done and results can be analysed.

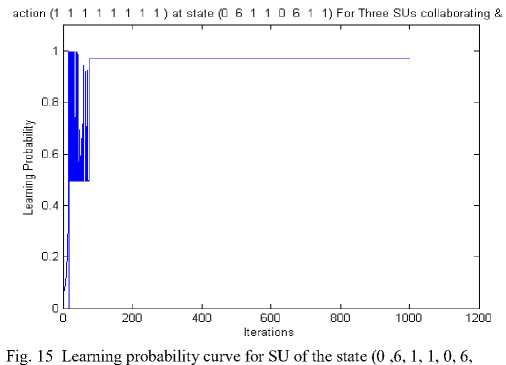
1, 1), three SUs collaborating, L=2

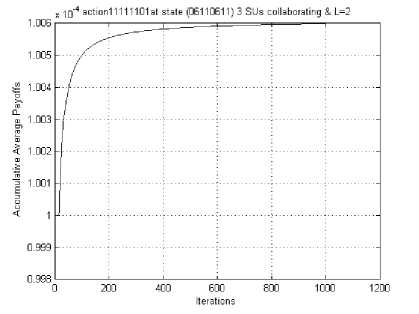
Fig. 16 Cumulative average reward curve for SU for the state (0, 6, 1, 1, 0, 6, 1, 1), three SUs collaborating, L=2

• V.    CONCLUSION

In this paper, we have considered the random jammer’s attack on secondary users (SUs) in cognitive radio network (CRN). We have proposed the multi-agent multi-band collaborative anti-jamming using reinforcement learning, where SUs collaborate with each other to combat single random jammer. Minimax-Q learning is used by the SUs independently to make individual decision then they collaborate to learn about the single jammer’s strategies. This paper demonstrates that in the multi-agent multi-band collaborative reinforcement learning agents (SUs) can learn faster about the jammer’s strategies and converge sooner than independent agents via sharing the learned policies. But this improvement in the learning probability is at the cost of increased communication.

The proposed collaborative game framework can be extended to model various anti-jamming mechanisms in other layers of a CRN, as it can model the dynamics because of the environment and the cognitive attackers as well. This collaborative approach can be advantageous for the other layers defence mechanism as well.

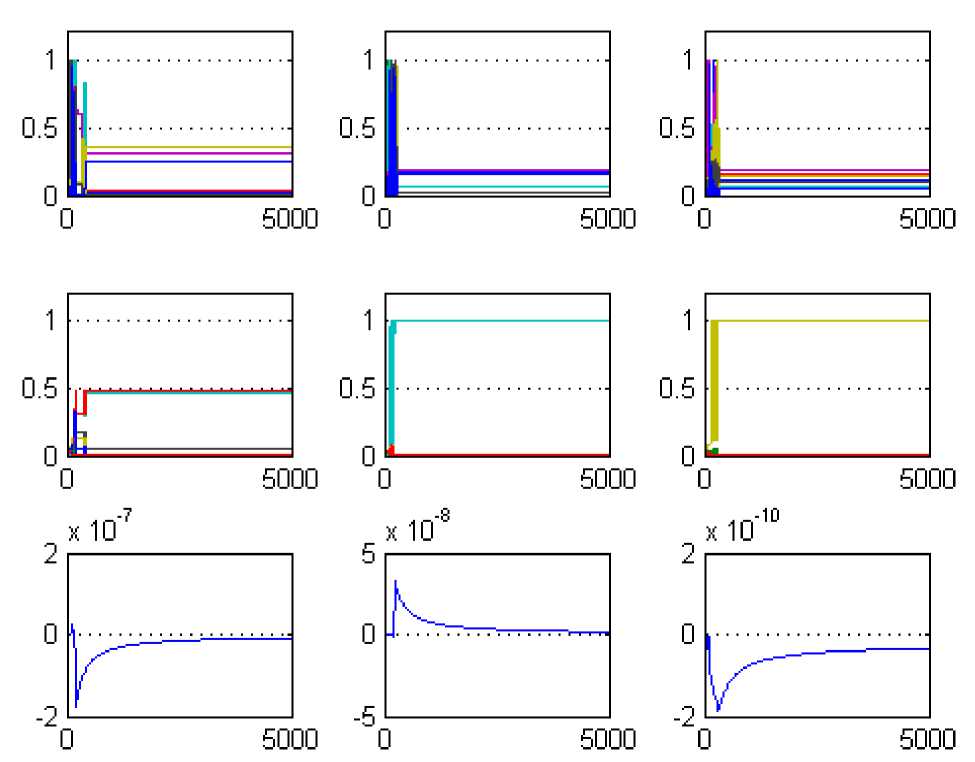
Fig. 17 Consolidated view of multi-agent scenario, L=1