Combination of Evolutionary Algorithms and Direct Search Approaches for Improving the Dynamic Performance of Grid Connected Solar Power System

ENGINEERING TECHNOLOGIES AND SYSTEMS

^ 0jjj|Mg

EDN:

Introduction. The Grid Connected Photovoltaic System comprises two fundamental control loops: an external loop responsible for overseeing the DC link voltage, and an internal control loop that regulates the inverter current. The primary element of any control loop is the proportional-integral controller and determining the appropriate gains for this controller is a difficult issue.

Aim of the Study. The study aimed to adjust the gains of the PI controllers in both static and dynamic irradiance scenarios for improving DC-link voltage by novel hybrid optimization method named Genetic Algorithm- Simulated Annealing and Genetic AlgorithmPattern search.

Material and Methods. In this paper we use two hybrid optimizations techniques called Genetic Algorithm- simulated Annealing and Genetic Algorithm- Pattern Search to adjust the gains of the PI controllers in both static and dynamic irradiance scenarios for improving DC-link voltage.

Results. Finally, this study presents comparison of DC-link voltage with six cases with manual tuning of PI controller, as well as PI controller by Genetic Algorithm- simulated Annealing, Genetic Algorithm- Pattern Search, Genetic Algorithm, Simulated Annealing and Pattern Search. The comparison showed by using Genetic Algorithm-Simulated Annealing, peak overshoot in DC-link voltage is 829.3 V while peak overshoot in DC-link voltage is 1 052 V when DC-link voltage is controlled by manual tuning of PI as well as significant reduction in peak time and settling time in DC-link voltage.

Discussion and Conclusion. The results achieved to strengthen the DC-link voltage under both static and dynamic irradiance conditions enable the sustaining of a constant DC-link voltage, which is essential for grid-connected photovoltaic systems. The comparison showed by using Genetic Algorithm- Simulated Annealing, peak overshoot in DC-link voltage is 829.3 V while peak overshoot in DC-link voltage is 1 052 V when DC-link voltage is controlled by manual tuning of PI as well as significant reduction in peak time and settling time in DC-link voltage.

Контент доступен по лицензии Creative Commons Attribution 4.0 License .

This work is licensed under a Creative Commons Attribution 4.0 License .

Сочетание эволюционных алгоритмов и методов прямого поиска для улучшения динамических характеристик солнечной энергетической системы, подключенной к сети

• A. Верма ^{1 н} , П. Тивари ¹ , Д. Д. Шарма ²

• ¹    Технологический университет имени Мадана Мохана Малавии, г. Горакхпур , Индия

• ²    Университет Махатмы Джотибы Пхуле Рохилкханд ,

г. Барейли, Индия

Введение. Фотоэлектрическая система, подключенная к сети, состоит из двух основных контуров управления: внешнего контура, отвечающего за контроль напряжения в звене постоянного тока, и внутреннего контура управления, регулирующего напряжение инвертора. Основным элементом любого контура управления является пропорционально-интегральный регулятор (ПИ-регулятор), но подбор соответствующих коэффициентов усиления этого регулятора является сложной задачей.

Цель исследования. Настроить коэффициенты усиления ПИ-регуляторов при статическом и динамическом облучении для улучшения напряжения в цепи постоянного тока с помощью двух гибридных методов оптимизации: «генетический алгоритм – искусственный отжиг» и «генетический алгоритм – поиск по шаблону».

Материалы и методы. Для настройки коэффициентов усиления ПИ-регуляторов при статическом и динамическом облучении для улучшения напряжения в цепи постоянного тока использовали два гибридных метода оптимизации: «генетический алгоритм – имитация отжига» и «генетический алгоритм – поиск по шаблону».

Результаты исследования. Сравнили напряжения в цепи постоянного тока в шести случаях использования ручной настройки ПИ-регулятора, при настройке ПИ-регулятора с помощью гибридных методов «генетический алгоритм - имитация отжига», «генетический алгоритм - поиск шаблонов», генетического алгоритма, «имитации отжига и поиска шаблонов». Сравнение показало, что при использовании гибридного метода «генетический алгоритм – имитация отжига» пиковое значение напряжения в цепи постоянного тока составляет 829,3 В, а при управлении напряжением в цепи постоянного тока с помощью ручной настройки пиковое превышение напряжения в цепи постоянного тока достигант 1 052 В ПИ, также наблюдается значительное уменьшение времени пикового напряжения и времени урегулирования напряжения в цепи постоянного тока.

Introduction. Oil, coal, natural gas, and nuclear power account for the considerable majority of the world energy needs, but they all have serious environmental consequences. One of the main causes of climate transformation is the greenhouse gas productions from burning fossil fuels, which is one of the most important crises facing people in this century [1]. Photovoltaic (PV) energy has gained a great deal of interest as a less polluting and noiseless resource with the potential to be utilized in rural areas [2]. Power electronics technology and digitization in the PV field have created it possible for PV applications to evolve quickly, especially Grid Connected Photovoltaic System (GCPS), which have grown from a few kW to over 100 MW [1]. The interface with the grid is now most crucial concerns for renewable energy penetration. Numerous control approaches are available in the literature, for photovoltaic (PV) interface systems with grid. However, it has difficulties with choosing the Proportional-Integral (PI) parameters correctly [3]. Trial and error method are employed to decide the PI controller parameters, which are mostly centered on the designer’s expertise and experience. In most cases, this is not the optimal method for constructing a controller, so meta-heuristic algorithms, such as evolutionary or swarm intelligence techniques, are employed [4].

When we use hybridized optimization techniques in GCPS purpose to augment performance and reliability by merging dissimilar optimization algorithms.

Literature Review. In context with this, the Z Source Inverter (ZSI), that is based on the Seagull Optimization Algorithm (SOA), is exploited to increase active power by offsetting the requirement for reactive power in the GCPS structure. The suggested approach can be evaluated through traditional methods such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO) and Grey Wolf Optimization, correspondingly by [5]. In this paper, observer based robust double integral sliding mode controller for GCPS is presented and the controller parameters are optimized via the water evaporation optimization algorithm. The conclusions of this work are validated against those of GA and PSO optimized controllers, therefore confirming the superiority of the suggested controller over others by [6]. To proposes the decoupled active and reactive power with the Salp swarm optimization (SSO) technique to govern the grid connected inverters and the suggested SSO approaches is equated to established optimization methods such as PI controller, GA and PSO by [7]. In this study, the total harmonic distortion is optimized using a genetic algorithm for three-phase three, five, seven, and nine levels inverters with varying switching angles and modulation index values by [8]. A two-loop study for grid-connected interleaved inverters with LCL filters is presented in this paper. The GA is used to optimize both the controller and the LCL filters in a dual-loop control approach by [9]

The author in [7] proposes the decoupled active and reactive power with the SSO technique to manage the grid connected inverters and the suggested SSO approaches is compared to established optimization methods such as PI controller, GA and PSO, However, detailed explanations of DC link voltage control and behavior of fitness function analysis of optimization techniques with iterations is ignored. The author in [8] the total harmonic distortion is optimized by a GA for three-phase three, five, seven, and nine levels inverters with varying switching angles and modulation index values, however, detailed explanations of fitness function analysis of GA algorithm is ignored.

In this paper GA, Pattern- Search, Simulated Annealing and combination of GA-PS and GA-SA algorithm is recommended to optimize the parameters of the PI controller and regulation of DCL voltage of the GCPS. The conclusions show that working with GA-SA and GA-PS offers optimal PI parameters that improve the dynamic performance of the GCPS compared to another methods. All the analysis is done on based by performance of DC link voltage, minimization of error in DCL voltage under normal and dynamic irradiance and behavior of various optimization techniques with number of iterations.

These key contributions are outlined in this paper summary:

• 1.    The objective is to enhance the performance of the GCPS through the optimal tuning of the PI-based Voltage Regulator (VR) and Current Regulator (CR), which are determined by the GA-SA and GA-PS methods in both static and dynamic irradiance scenarios for improving DC-link voltage.

• 2.    The hybrid optimization technique integrates both the GA-SA and the GA-PS. The suggested algorithm is verified and validated on a GCPS. Moreover, its outcomes are compared with those of the other frequently used techniques such as GA, SA, PS and PI without optimization centered on the uniform objective function to verify its accuracy and validity.

• 3.    Comparative analysis of minimization of error in DCL voltage under variation of irradiance by using GA-SA and GA-PS methods.

• 4.    Behavior of fitness function analysis of optimization techniques with iterations.

The residual divisions of this work are systematized as follows: The GCPS model is represented in Segment III. The discussion of the objective function of the optimization issue will be explored in Segment IV and brief description of hybrid optimization technique as well as block diagram of PI tuning by GA-SA, GA-PS, SA, PS, and GA. Section V comprises the several optimization techniques used in the paper and comparison of different optimization algorithms-based PI controller’s gains. The end result is examined in Segment VI, and, lastly, the conclusions are withdrawn in Section VII.

System description. The system buildup of the GCPS is given in Figure 1. PV array, boost converter with MPPT module, inverter control, local loads, and grid make up the GCPS system.

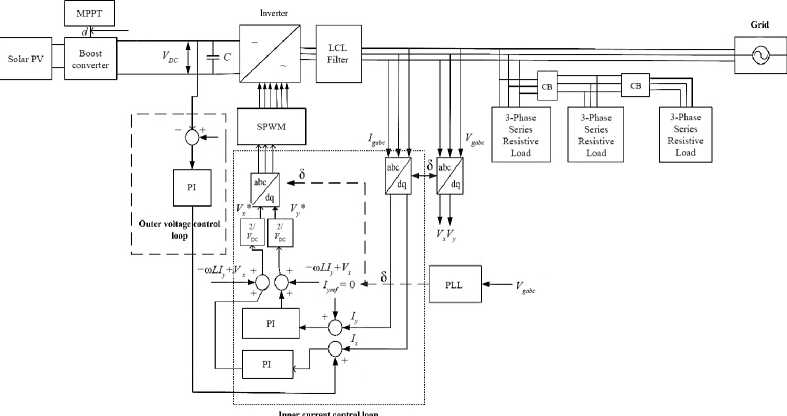
F i g. 1. GCPV system structure

Note: SPWM – sinusoidal pulse width modulation; PLL – phase locked loop; CB – circuit breaker. Source: the diagram is compiled by the authors of the article from the materials [10].

The PV system, as explained in this study, primarily operates with a PV array including 47 parallel-connected branches. Each branch is composed of 10 PV modules, resulting in a peak power output of 100.2 kWp under solar radiation of 1 000 W/sqm. The boost converter raises DC voltage from approximate 295 V to 600 V. For inverter, 3-armed converter structure is used. The inverter control section is exploited to regulate the DC-link voltage and the required value of the inverter output. The MPPT is utilized to obtain the peak power point of the PV panels. The control scheme employed to the Inverter, as illustrated in Figure 1, primarily contains dual cascaded loops: an exterior voltage control loop that modulates the DCL voltage and a fast internal current control loop that controls the grid current. All control loops are primarily regulated by PI controllers, with their gains optimally determined through the application of GA-SA and GA-PS to enhance the dynamic performance of the GCPS. The inverter controller comprises of PLL, VR and CR shown in Figure 2. The assessment of voltage and currents takes place at the point of common connection. As a result, the original frame signals undergo a transformation into a synchronized orthogonal frame ( d - q ) that rotates at the angular frequency of the grid. The symbol δ signifies the rotating frame angle employed for the purpose of transferring voltages and currents from the original frame signal to the ( d - q ) frame, and vice versa. The V x , V y and I x , I y are voltages and currents in ( d - q ) frame is expressed by eqs. (1), (2):

V x 1		cos S	cos ( S- 120 ° )	cos ( S + 120 ° ) ’	к ’ ga
V y	= 0.81	- sin S	- sin ( S- 120 ° )	- sin ( S + 120 ° )	V gb	;         (1)
V 0		_ 0.5	0.5	0.5	_ Vgc _

I x I y . 1 0 .

= 0.81

cos 5

- sin 5

0.5

cos ( 5- 120 ° )

- sin ( 5- 120 ° )

0.5

cos ( 5 + 120 ° )

- sin ( 5 + 120 ° )

0.5

I

I gc _

,

V ga ’ V gb ’ V gc and Iga ’ I_gb ’ Igc are the three-phase voltages and currents of the grid accordingly.

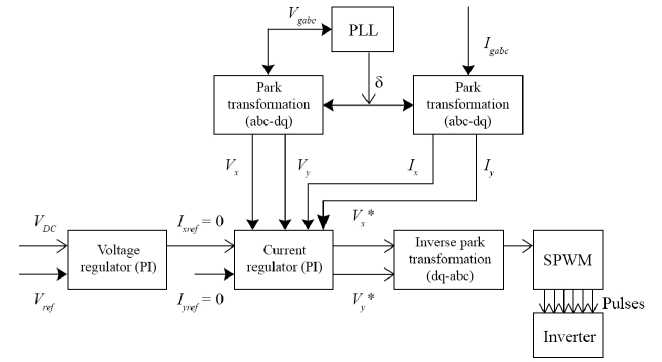
F i g. 2. Inverter control structure

Source: the diagram is compiled by the authors of the article from the materials [11].

Objective function. Numerous objective functions or fitness functions centered on error performance index are available, these criteria indices are Integral Squared Error, Integral Absolute Error, Integral Time-Weighted Absolute Error (ITAE) and Integral Time Square Error. In GCPS, assessment of optimal parameters of PI controllers of inverter control structure is very crucial. In this paper the ITAE based on error performance index is formulated as objective functions to be minimized for the VR and CR, with the purpose of achieve the optimal PI controller parameters ( K p and K . ) in the VR and CR [12]. The objective function of the system can be articulated as follows:

min

J ( x ) = £ max te (t )| dt,

T _max is the simulation time in seconds and the error signal is described as for voltage regulator and current regulator given below.

Error signal for voltage regulator is defined as e ₁ ( t ) = Reference voltage-DC link voltage. Error signal for current regulator is defined as e ₂ ( t ) = Reference current-measured current.

In the GCPS, the problem constraints consist of the optimized parameters of PI controllers, with bounds defined as follows:

lb < KV < Ub; lb < K/R < Ub; lb < k^ < Ub; lb < K^ < Ub, where KpVR and KpCR are the proportional controllers gains of VR and CR respectively; KiVR, k,cr are the integral controllers gains of VR and CR, respectively; lb and ub are lower and upper bound respectively.

Hybrid optimization techniques. The performance of optimization techniques may vary for a given problem. In numerous instances, the utilization of hybrid techniques, using this difference, may yield superior results [13]. In this paper we use two hybrid optimizations techniques called GA-SA and GA-PS. Evolutionary algorithms, such as the genetic algorithm, are recognized as very resilient and potent global optimization methodologies employed to address complex problems characterized by multiple local optima. Nevertheless, these algorithms exhibit large computational demands and demonstrate suboptimal convergence performance. Conversely, SA and PS, when implemented as local search algorithms, can achieve convergence in a shorter amount of time; however, they do not possess a global perspective. The integration of global and local search algorithms presents the potential to harness the benefits of both optimization strategies while mitigating their respective drawbacks [14]. In GA-SA or GA-PS the result from GA is as the initial point for another optimization solver to execute a faster and more proficient local search.

Block diagram of PI tuning by various optimization techniques. The block diagram of the PI tuning by various optimization process is shown in below Figure 3. The choice of the optimization method by GA-SA, GA-PS, SA, PS, GA to determine the parameters ( K_p and K_i ).

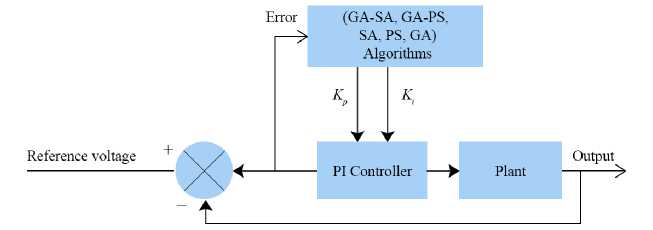
F i g. 3. PI tuning of various optimization techniques

Source: the diagram is compiled by the authors of the article from the materials [15].

Material and Methods. The optimization algorithm is a sequential procedure that commences with an arbitrary initialization and gradually approaches an optimal outcome through a series of iterations [12]. The primary objective of this study is to determine the optimal parameters for PI controllers gain for both VR and CR in an inverter controller in GCPS by various optimization techniques illustrated given below.

Genetic Algorithm-Simulated Annealing ( GA-SA ) . In this work, we have applied the GA and SA in hybrid manner to attain the optimum parameters for the PI controllers gain of VR and CR. In the context of optimization algorithms, the GA-SA framework is employed, where GA represents the global search component and SA denotes the local search component. The GA has the benefits of robust global optimization capability, quick speed, robust versatility, and simple implementation. Nevertheless, a notable limitation of this approach is its suboptimal performance in local search, leading to reduced search efficiency, particularly during the later stages of the optimization process. Conversely, the SA algorithm possesses proficient local search capabilities to compensate for the deficiencies of the GA [16]. The algorithms primarily consist of three key stages: initialization and population generation, iteration, termination and evaluation. Each algorithms share the same population generation [17]. The flow chart of GA-SA is shown in Figure 4.

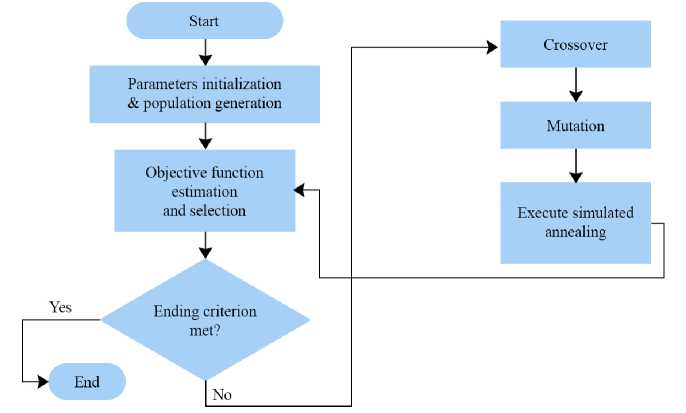
F i g. 4. The flow chart of GA-SA

Source: the diagram is compiled by the authors of the article from the materials [17].

Genetic Algorithm-Pattern Search ( GA-PS ) . In GA-PS algorithm combines both GA and PS algorithm with the purpose of acquire the optimum parameters for the PI controllers gain of VR and CR. The GA serves as the primary optimization technique by using its ability to do global searches. Subsequently, the Pattern Search (PS) algorithm is utilized to refine the optimal solution obtained from GA throughout each evolutionary iteration [18]. The use of GA may result in a prolonged convergence process. In contrast, employing solely the PS algorithm would result in a solution that is highly unstable and susceptible to variations in beginning conditions. Hence, the integration of both algorithms yields outcomes that are more reliable and obtained with greater efficiency [19]. The flow chart of GA-PS is shown in Figure 5.

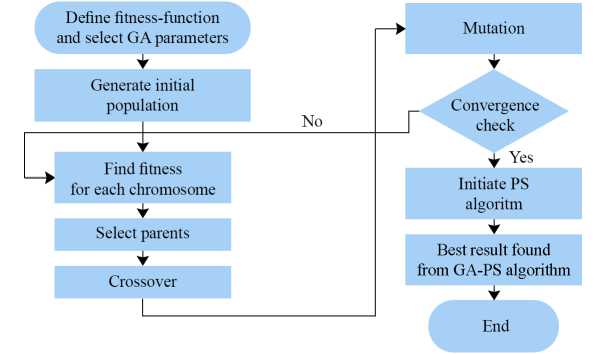
F i g. 5. The flow chart of GA-PS

Source: the diagram is compiled by the authors of the article from the materials [18].

Pattern search optimization techniques. PS algorithm to attain the optimum parameters for the PI controllers gain of VR and CR. The PS optimization technique is a derivative-free evolutionary approach as well as direct search method that is compatible for addressing a diverse range of optimization problems that fall beyond the boundaries of conventional optimization methods. In general, the PS optimization technique possesses the advantage of exhibiting a straightforward conceptual framework, facilitating ease of implementation and computational efficiency. In contrast to other heuristic algorithms, such as the GA, the PS algorithm offers a versatile and well-balanced operator that serves to improve and adjust both global and local search capabilities. The PS method operates by iteratively calculating a series of points that may or may not converge towards the ideal position [18]. The flow chart of PS is shown in Figure 6.

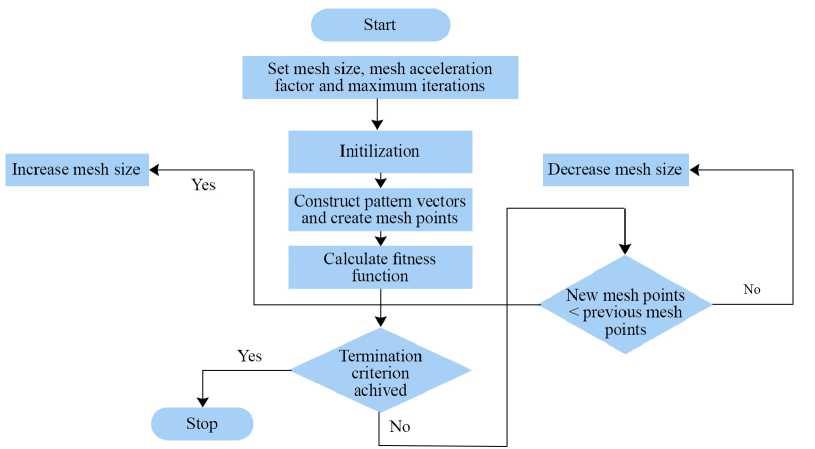
F i g. 6. Flow chart for Pattern search

Source: the diagram is compiled by the authors of the article from the materials [20].

Simulated Annealing. SA to attain the optimum parameters for the PI controllers gain of VR and CR. Simulated Annealing (SA) is a metaheuristic algorithm that is commonly used to search for the global optimum of a given function. This approach is mostly employed when prioritizing the identification of a satisfactory local optimal outcome over the attainment of an exact global optimal solution within a specified timeframe [21]. The concept of SA is based on an analogy to the physical annealing process. The flow chart of SA is shown in Figure 7.

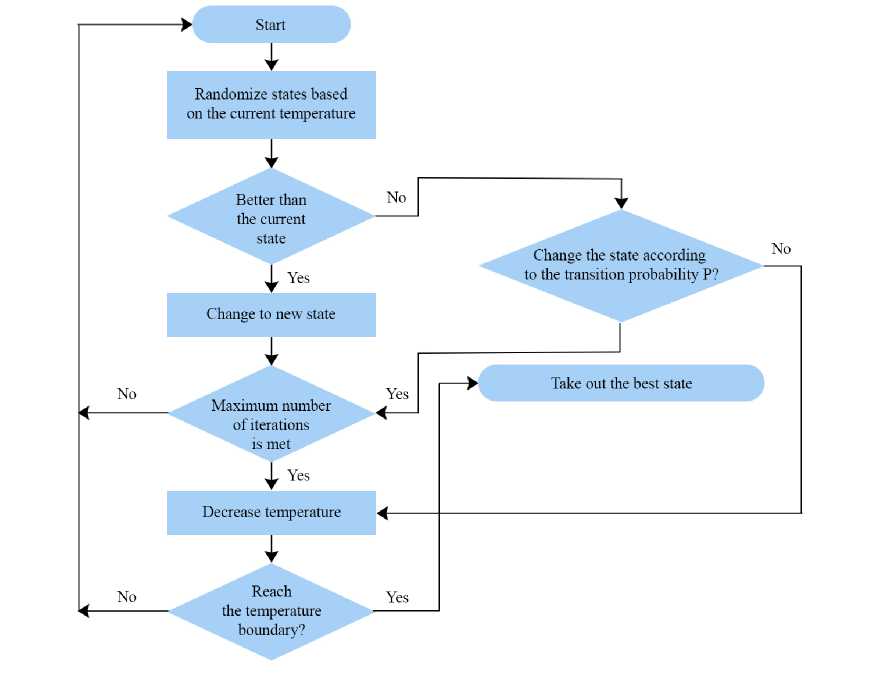
F i g. 7. Flow chart of Simulated annealing

Source: the diagram is compiled by the authors of the article from the materials [22].

Genetic Algorithm. GA algorithm to attain the optimum parameters for the PI controllers gain of VR and CR. The GA is an optimization technique inspired by genetic principles and natural selection. The GA enables a population of several individuals to evolve under defined selection criteria to a state that optimizes “fitness” (i.e., minimizes the cost function). The Genetic Algorithm commences, identical to any other optimization technique, by establishing the optimization variables, the cost function, and the associated costs [23]. The flow chart of GA is shown in Figure 8.

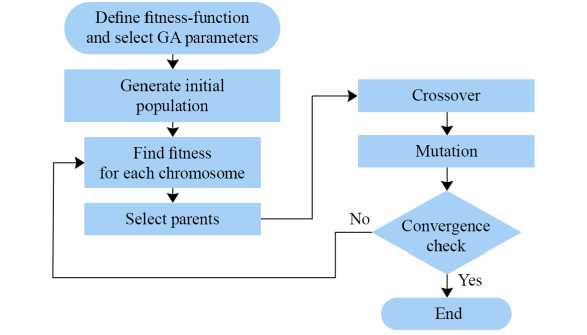
F i g. 8. Flow chart of genetic algorithm

Source: the diagram is compiled by the authors of the article from the materials [24].

Various optimization techniques-based PI controllers gains. In this subsection the attained PI controllers gains of various optimization techniques and without optimization are given which are listed in Table 1.

T a b l e 1

The attained PI controllers gains of various optimization techniques and without optimization

Approach	Voltage regulator		Current regulator
	K p	K i	K p	K i
PI (Hit and trial)	0.00001	320	10	20
SA	0.90	14.56	60.56	63.42
PS	1	54	23	368
GA	1.16	13.78	103	303
GA-PS	1.16	12.78	100	397
GA-SA	1.16	10.78	79.01	390

Various optimization approaches parameters. In this subsection various optimization parameters like population size or search agents’ number, number of iterations, lower and upper bound range of voltage and current regulator are given which are listed in Table 2.

T a b l e 2

Various optimization approaches parameters

Parameters	GA-SA	GA-PS	GA	PS	SA
Population size	25	25	25	Not applicable	Not applicable
Iterations	50	50	50	50	50
Range of PI gain voltage regulator	[0 400]	[0 400]	[0 400]	[0 400]	[0 400]
Range of PI gain current regulator	[0 400]	[0 400]	[0 400]	[0 400]	[0 400]

Results. This segment aims to demonstrate the dynamic performance of GCPV system using without optimization, and algorithms such as GA-SA, GA-PS, GA, PS, and SA. Additionally, it includes a comparative analysis of DC link voltage with and without optimization, the minimization of error in DC link voltage, and an analysis of optimization techniques centered on the number of iterations. The solar intensity is changed at t = 0.1 s from 1 000 W/sqm to 400 W/sqm to calculate the optimal setting of the PI controller gains.

PI tuning. This section is employed to illustrating the dynamic performance of the GCPV system when the PI parameters are achieved from the hit and trial method.

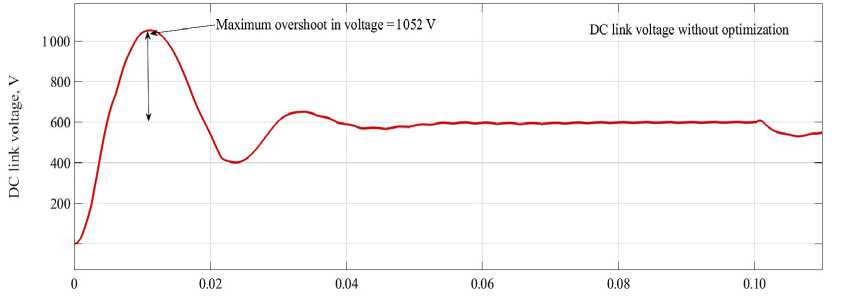
DCL voltage without PI optimization. Figure 9 shows that the DCL voltage from conventional PI controller, as can be seen maximum overshoot recorded is 1 052 V and settling time is 0.07 s.

Time, s

F i g. 9. DCL voltage without PI optimization

Source: hereinafter in this article the figures are made by the authors of the article with the use of the program Matlab Simulation.

Minimization of error in DCL voltage without optimization. At t = 0.1 s, the irradiance undergoes a dynamic change, transitioning from a 1 000 W/sqm to 400 W/sqm. As illustrated from below Figure 10 the errors reach around at t = 0.1 s is 50.57 V and settled after some time, this condition is not healthy for GCPV system. Figure 10 shows that the minimization of error in DCL without optimization.

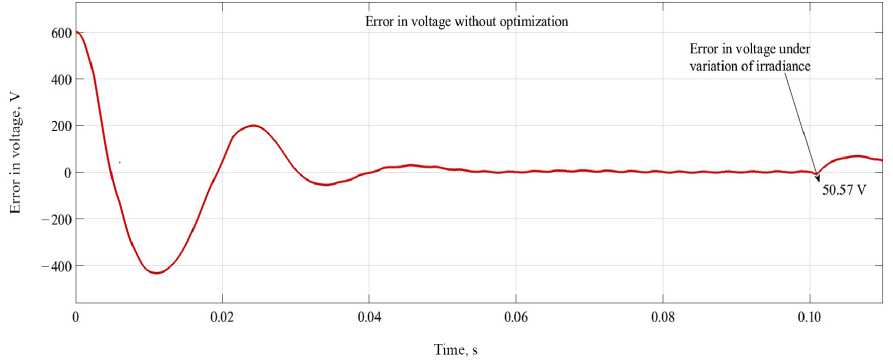
F i g. 10. Error in DCL voltage without PI optimization

PI controller’s optimization by GA-SA. The optimally measured values are 1.16 and 10.78 for K_p and K_i of the PI based VR, respectively as well as 79.01 and 390 for K_p and K_i of the PI based CR, respectively.

DC link voltage with GA-SA optimization. Figure 11 shows that the DCL voltage optid with GA-SA, as can be seen maximum overshoot in voltage recorded as 829.3 V and settling time is 0.037 s.

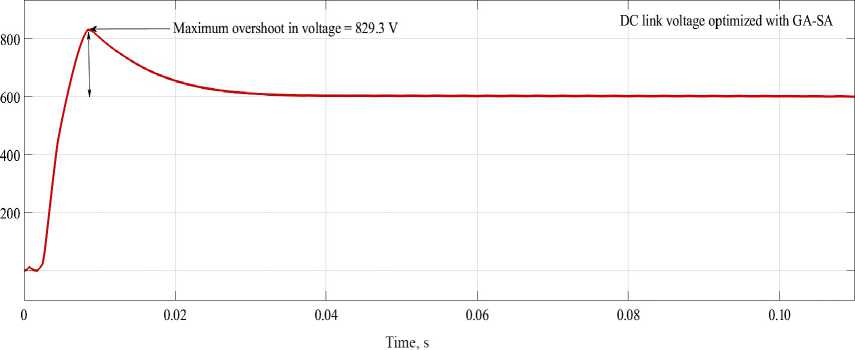
F i g. 11. DCL voltage optimized with GA-SA

Minimization of error in DCL voltage with GA-SA optimization. Solar insolation is varied as of 1 000 W/sqm to 400 W/sqm at t = 0.1 s. As illustrated from Figure 12 the errors reach around at t = 0.1 s is 0.6090 V very close to zero.

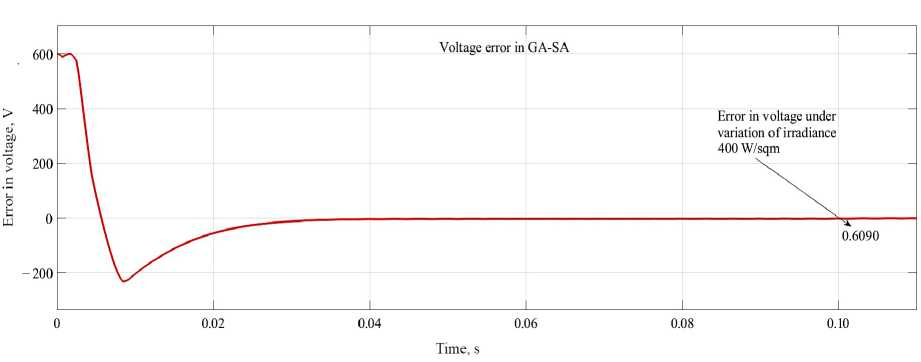
F i g. 12. Error in DCL voltage optimized with GA-SA

PI controller’s optimization by GA-PS. The optimally measured values are 1.16 and 12.78 for K_p and K_i of the PI based VR, respectively as well as 100 and 397.7 for K_p and K_i of the PI based CR, respectively.

DC link voltage with GA-PS optimization. Figure 13 shows that the DCL voltage optimized with GA-PS, as can be seen maximum overshoot in voltage recorded as 830 V and settling time is 0.0371 s.

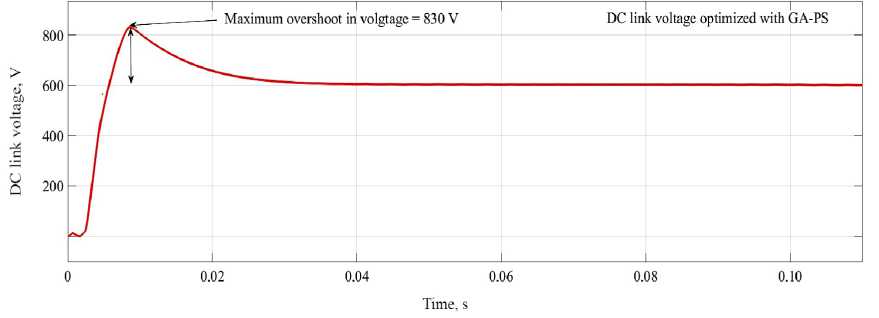
F i g. 13. DCL voltage optimized with GA-PS

Minimization of error in DCL voltage with GA-PS optimization. Solar insolation is varied as of 1 000 W/sqm to 400 W/sqm at t = 0.1 s. As illustrated from Figure 14 the errors reach around at t = 0.1 s is 0.6078 V very close to zero.

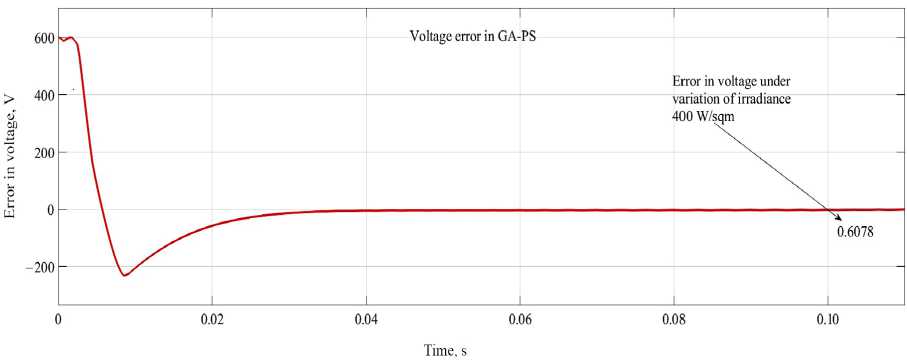
F i g. 14. Error in DCL voltage optimized with GA-PS

PI controller’s optimization by simulated annealing technique. The optimally measured values are 0.90 and 14.56 for K_p and K_i of the PI based VR, respectively as well as 60.56 and 63.42 for K_p and K_i of the PI based CR, respectively.

DC link voltage with simulated annealing optimization. Figure 15 shows that the DCL voltage optimized with simulated annealing, as can be seen maximum overshoot in voltage recorded as 869.5 V and settling time is 0.039 s.

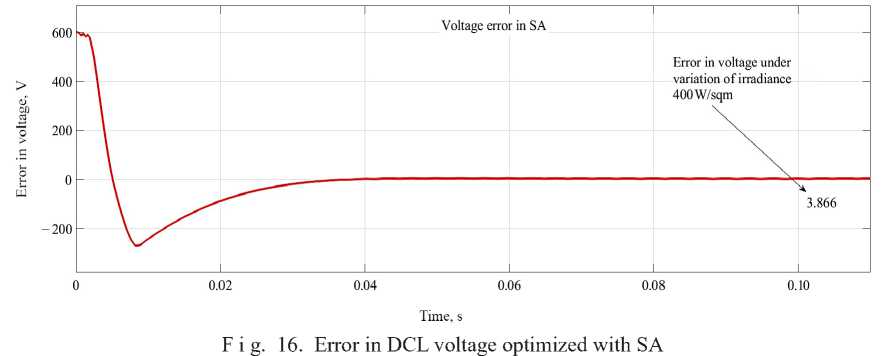
Minimization of error in DCL voltage with simulated annealing optimization. Solar insolation is varied as of 1 000 W/sqm to 400 W/sqm at t = 0.1 s. As illustrated from Figure 16 the errors reach around at t = 0.1 s is 3.866 V.

PI controller’s optimization by pattern search technique. The optimally measured values are 1 and 54 for K_p and K_i of the PI based VR, respectively as well as 23 and 368 for K_p and K_i of the PI based CR, respectively.

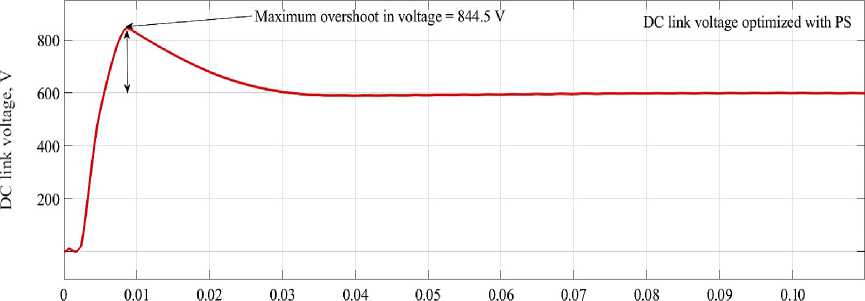
DC link voltage with pattern search optimization. Figure 17 shows that the DCL voltage optimized with pattern search, as can be seen maximum overshoot in voltage recorded as 844.5 V and settling time is 0.063 s.

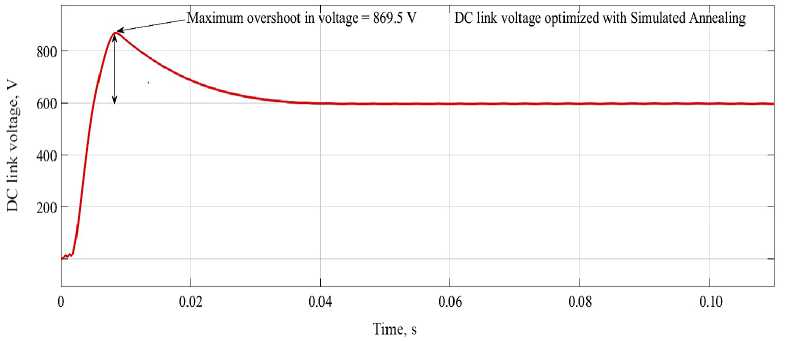
F i g. 15. DCL voltage optimized with SA

Time, s

F i g. 17. DCL voltage optimized with PS

Minimization of error in DCL voltage with pattern search optimization. Solar insolation is varied as of 1 000 W/sqm to 400 W/sqm at t = 0.1 s. As illustrated from Figure 18 the errors reach around at t = 0.1 s is 1.643 V.

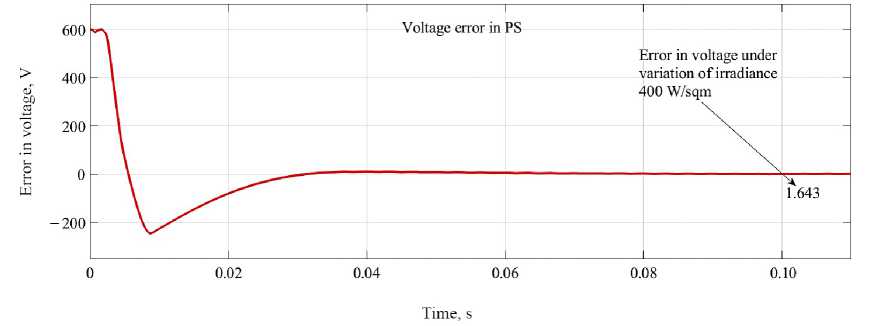
F i g. 18 Error in DCL voltage optimized with PS

PI controller’s optimization by genetic algorithm technique. The optimally measured values are 1.16 and 13.78 for K_p and K_i of the PI based VR, respectively as well as 103 and 303 for K_p and K_i of the PI based CR, respectively.

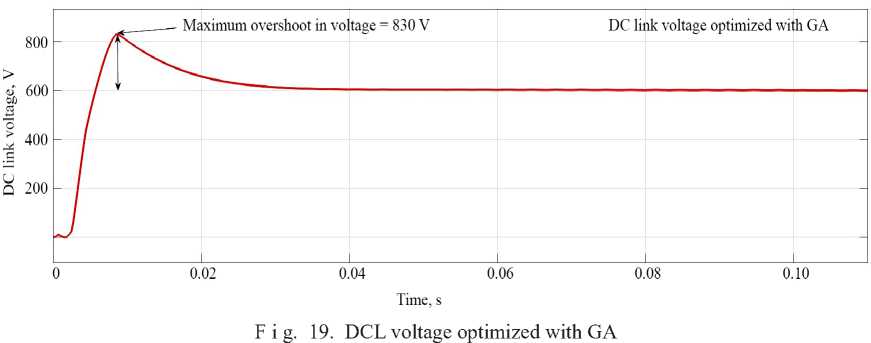
DC link voltage with genetic algorithm optimization. Figure 19 shows that the DCL voltage optimized with genetic algorithm, as can be seen maximum overshoot in voltage recorded as 830 V and settling time is 0.03 s.

Minimization of error in DCL voltage with genetic algorithm optimization.

Solar insolation is varied as of 1 000 W/sqm to 400 W/sqm at t = 0.1 s. As illustrated from Figure 20 the errors reach around at t = 0.1 s is 0.6152 V.

Comparative analysis of DC link voltage based on optimization. A comparison of the GA-SA and GA-PS method with other renowned PI tuning methods examined in this paper was made for GCPV system on the basis of DC link voltage peak, rise time, peak time and settling time and the achieved results are illustrated in Table 3.

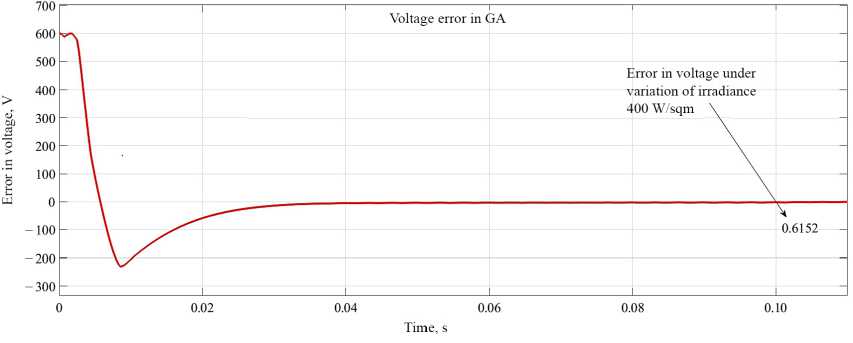
F i g. 20. Error in DCL voltage optimized with GA

Comparative analysis of DC link voltage based on optimization

T a b l e 3

PI tuning	DC link voltage peak, V	Maximum overshoot in DC link voltage, %	Peak time tp , s	Settling time ts , s	Rise time tr , s
PI	1 052	75.33	0.0110	0.080	0.0048
SA	869.5	44.90	0.0083	0.039	0.0050
PS	844.5	40.75	0.0086	0.060	0.0055
GA	830	38.33	0.0086	0.036	0.0057
GA-PS	830	38.33	0.0085	0.036	0.0057
GA-SA	829.3	38.21	0.0088	0.036	0.0057

It was concluded that the GA-SA, GA-PS and GA offers a enhanced solution for the PI gains optimal selection than other renowned algorithms in terms of transient response indicators, but GA-SA and GA-PS they have minimum fitness function value of convergence performance that’s why GA-SA and GA-PS used in this paper. Convergence process of particular optimization explained in section 6.9. For example, the GA-SA, GA-PS and GA algorithm based on PI tuning provided 49%, 14.63% and 6.74% less overshoot than that of PI without optimization, SA and PS respectively. It can be also seen that the settling time, rise time and peak time of the GA-SA and GA-PS optimization methods is less than that of PI without optimization, SA and PS methods. Figure 21 shows the comparative analysis of DCL voltage with and without optimization.

Comparative analysis of minimization of error in DCL voltage under variation of irradiance. As illustrated from Figure 22 the errors reach around under variation of solar insolation from 1 000 W/sqm to 400 W/sqm at t = 0.1 s, for GA-SA optimization techniques the error in DCL voltage at variation of irradiance is 0.6090 V and for GA-PS is 0.6078 V as well when optimized by GA, SA and PS the error in voltage under variation of irradiance is 0.6152, 3.8660 and 1.6430 respectively. Clearly shows that when technique is hybridized the error in voltage is less under variation of irradiance.

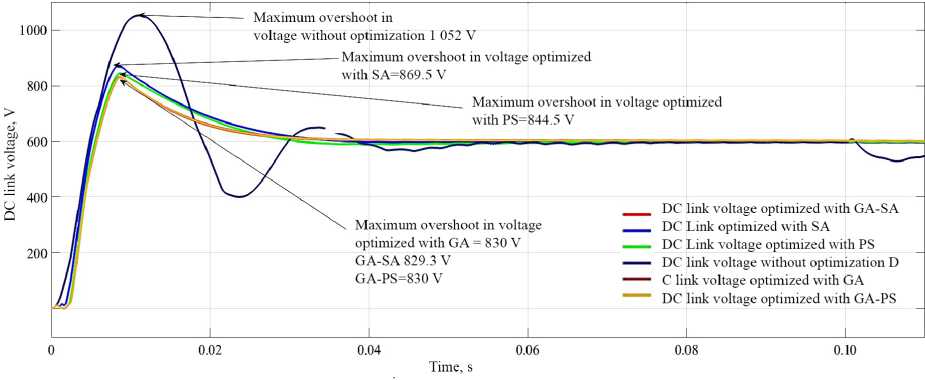
F i g. 21. Comparative analysis of DCL voltage with and without optimization

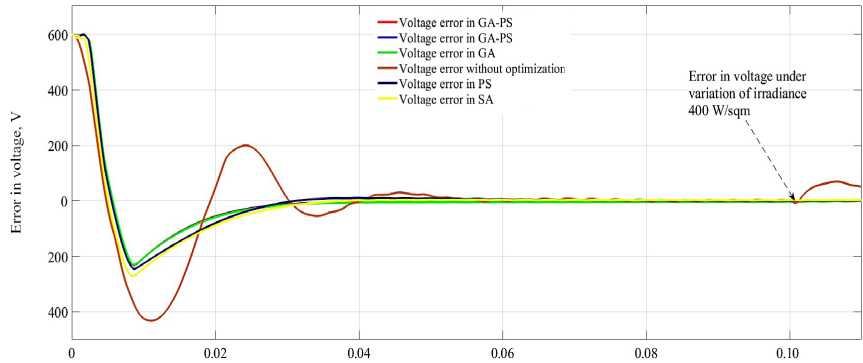
Time, s

F i g. 22. Comparative analysis of error in DCL voltage with and without optimization

Behavior of various optimization techniques with number of iterations. Figure shows the convergence behavior of the suggested GA-SA and GA-PS in solving the minimization of error in voltage and current regulator for obtaining optimal PI parameters. It can be observed that the ITAE exhibited a decrease as the number of iterations increased. In addition, the ITAE serves as the fitness function, therefore minimizing ITAE leads to progress towards the optimal vicinity.

When evaluating a convergence curve in the optimization process, it is crucial to consider two key parameters: the convergence rate and the ultimate minimized or maximized value of the objective function. The first parameter determines the rate at which the convergence curve progresses, whereas the secondary parameter offers explicit insights on the value of the solution obtained through the optimization procedure. It is fairly clear in above figure that the GA-SA and GA-PS optimization techniques gets a suitable solution in minimizing the stated objective function with higher solution quality. The minimized value for the objective function for the GA-SA process is 0.267879857 and is obtained in the 32nd iteration of the simulation as well as the minimized value for the fitness function for the GA-PS process is 0.259750701 and is obtained in the 48th iteration of the simulation.

It is obvious from above figure that the GA-SA and GA-PS based PI tuning method provided a better solution as compared to the GA, SA and PS based methods for the identical system and optimization parameters. Each algorithm was run 5 times to optimize the identical fitness function. The study aimed to minimise the defined objective function, and hence the lowest value achieved by each method was selected and depicted in the above figure. Increasing the number of iterations could potentially result in a further decrease in the value of the objective function. However, it is crucial to examine the trade-off between the reduction in the objective function and the time required for the optimisation process. Figure 23 shows the convergence curve of various optimization techniques as well as Figure 24 shows the objective function value of various optimization techniques.

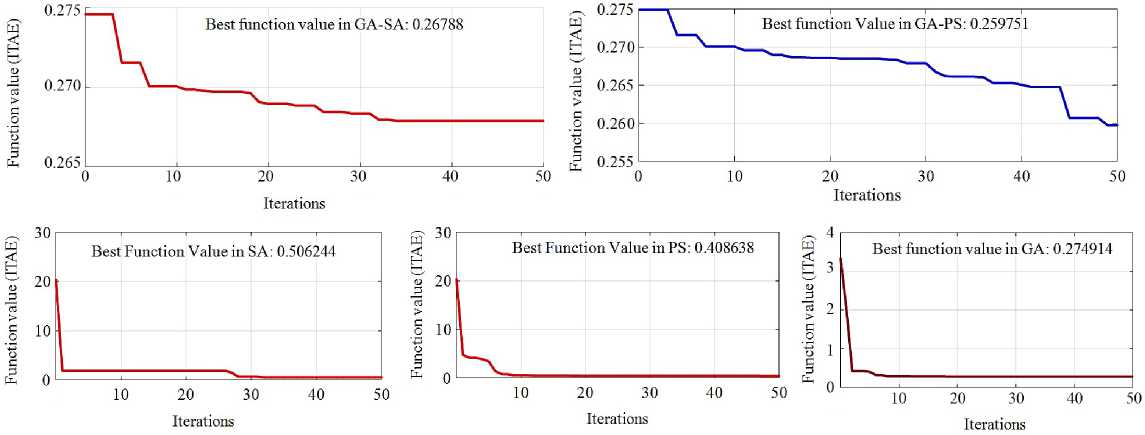
F i g. 23. Comparative analysis of convergence curve of various optimization techniques

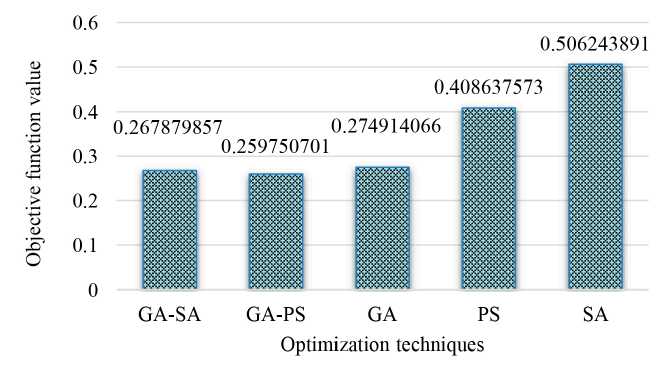
F i g. 24. Objective function value of various optimization techniques

Discussion and Conclusion. In this work, the DC link voltage regulation of the PV system is proposed. The regulation is achieved by optimizing the parameters of the PI controller. In this work, a new algorithm known as GA-SA and GA-PS is bring together to valuate these parameters optimally. Optimization strategies yielded superior outcomes compared to manual calculations. In order to demonstrate the effectiveness of the adopted algorithm, its outcomes are evaluated to those of the formerly utilized algorithms such as SA, PS and GA at the same objective function. As the aim of the study minimized value for the fitness function for the GA-SA process is 0.267879857 and is obtained in the 32nd iteration of the simulation as well as the minimized value for the fitness function for the GA-PS process is 0.259750701 and is obtained in the 48th iteration of the simulation. GA-SA and GA-PS proofs it’s superior rather than GA, SA, PS based on minimization of fitness function. Characteristics of GA-SA, GA-PS and GA in settling time is same. With the help of hybrid optimization techniques optimizing power grid operations and energy distribution.