Combination of Hybrid Chaotic Encryption and LDPC for Secure Transmission of Images over Wireless Networks

The wireless communication medium, as opposed to the wired counterparts, is noisy and open to intruders. Hence, an additional level of error protection and security is required to make the wireless network as reliable and secure as the wired network [1]. Error control codes (ECC) are an important issue in wireless transmission, and are used to protect data from channel errors. The issue of using cryptography, secure ciphers in the wireless noisy channel is that the very same property that gives ciphers their cryptographic strength makes them sensitive to channel errors. This sensitivity causes retransmissions thus reducing the overall throughput. To improve the throughput in noisy environments, channel coding is performed after encryption. There are many factors that cause the output of a communication channel to be different from its input. Among these factors are attenuation, nonlinearities, bandwidth limitations, multipath propagation and noise [2]. For reliable communications, to improve the throughput in noisy environments, channel coding is performed after encryption.

There are many researchers who have introduced error correction and encryption in communication networks that have been addressed independently such as in [3-4]. Several researchers have studied the trade-off between encryption and error correction by trying to combine these functionalities in one unit. For instance, Gligoroski et al [5].

In this paper, we introduce a new algorithm which combines encryption and coding in one algorithm; we propose hybrid chaotic encryption with LDPC. The paper will be organized as follows: section 2 gives a brief discussion of channel coding techniques as LDPC and Turbo code technique. Section 3 presents a comparison between the performance of LDPC and Turbo. Section 4

defines the performance parameters. Section 5 explains the proposed scheme. Experimental results are discussed in section 6. Finally, Section 7 concludes the paper.

• II.    Channel Coding

Channel coding techniques are divided into two main types; block codes and convolution codes. In this section we introduce two different algorithms one is LDPC code as a type of block code, and the other is Turbo code as a type of convolution code [6-7].

• A.    LDPC Code

LDPC is an error correcting code used in noisy communication channels to reduce the probability of loss of information. With LDPC, this probability can be reduced as small as desired, thus the data transmission rate can be as close to Shannon's limits [8].

Nowadays, LDPC has made its way into some modern applications such as 10GBase-T Ethernet, Wi-Fi, WiMAX, Digital Video Broadcasting (DVB). Since 1993, with the invention of turbo codes, researchers have switched their focus to finding low complexity codes which can approach Shannon channel capacity [9-10].

If a code uses n bits to provide error protection to k bits of information, it is called a (n, k) block code. In the case of image transmission, larger n and k, a matrix representation of the codes is used. This representation includes a generator matrix, G, and a parity-check matrix, H. Given a message p, the codeword c will be the product of G and p with entries modulo 2:

c = p × G (1)

Given the received codeword y, the syndrome vector is z = y× H (2)

If z = 0 then the received codeword is error-free, else, the value of z is the position of the flipped bit. For more details about LDPC coding and decoding refer to [9-10].

• B.    Turbo Channel Coding

Turbo codes use an interleaver between two parallel or serial encoders as shown in figure 1 the existence of the interleaver results in very large code word lengths with excellent performance, particularly at low SNRs. Using these codes, it is possible to get as close as 0.7 dB to the Shannon limit at low SNRs. The turbo encoder consists of two constituent codes separated by an interleaver of length N. Because the encoders are systematic, each encoder generates the N-information bits applied to its input followed by N parity check bits. After the encoding, the N information bits and the 2N parity check bits of the two encoders, a total of 3N bits, are transmitted over the channel. Therefore, the overall rate is R = N/3N =1/3.

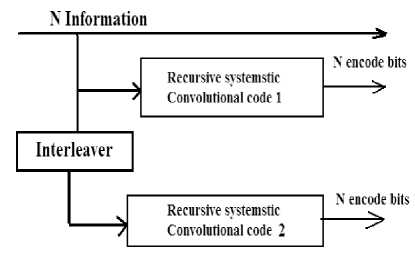
Fig. 1. Block diagram of Turbo encoder

The interleaver in turbo codes is usually very long, of the order of thousands of bits. Pseudorandom interleavers perform well, although some improvement in the performance of the code can be obtained by clever choice of the interleaver. This improvement is more noticeable at short interleaver lengths. Due to the existence of the interleaver, it is, in most cases, impossible to return both codes to the all-zero state.

Since turbo codes have two constituents-code components, an iterative algorithm is appropriate for their decoding. Any decoding method that yields the likelihood of the bits as its output can be used in the iterative decoding scheme as shown in figure 2. One such decoding scheme is the maximum a posteriori (MAP) decoding method.

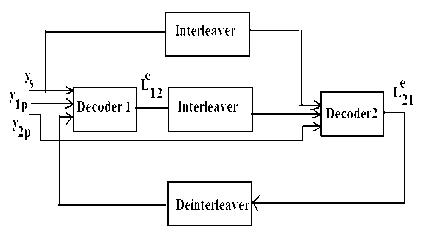
Fig. 2. Block diagram of Turbo decoder

For more details about turbo coding and decoding, refer to [11].

• C.    Performance Parameters

The quality of the received image can be measured by many performance parameters such as the Peak Signal to Noise Ratio (PSNR). It is most commonly used as a measure of the quality of a reconstructed image. It is most easily defined via the Mean-Squared Error (MSE) which for two m × n monochrome images I and K where one of the images is considered a noisy approximation of the other. It is defined as:

m — 1 n — 1

ME = — EEI I¹ ( i , j ) — K ( i , j )ll 2 . m x n , = o j = o

The PSNR is defined as:

PSNR = 10log10

2552 ^ MSE J

The other parameters are Message Error Rate (MER) and Bit Error Rate (BER), MER define as = (No. of messages received in Error after error correction) / (Total no. of messages transmitted) [6].

BER quantifies the reliability of the entire radio system it can be defined as: BER = Errors/Total Number of Bits with a strong signal and an unperturbed signal path, this number is too small as to be insignificant. It becomes significant when we wish to maintain a sufficient signal-to-noise ratio in the presence of imperfect transmission through electronic circuitry.

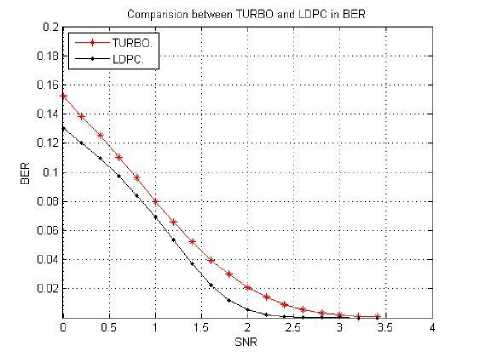
Fig. 3. BER versus SNR of the received cameraman image with Turbo and LDPC

• III.    Comparison Between Performance Of Turbo And Ldpc

  The comparison of different channel coding techniques will help to identify the most efficient one for a particular application. After the remarkable work [12] of Claude Shannon in 1948 it is necessary to transmit errorless data mainly in digital communications which are being used for multimedia communications for small hand held devices, such as Mobile Phones, Pagers, PDAs etc.

We compare between the performance of LDPC and turbo. In BER and processing time to determine the best for use in our proposed algorithm, we use the two algorithms with the following parameters.

The time is measured from the time the image inputs to be encoded to the end of the decoding of the image then reconstructing the decoded image.

Table 1.Simulation parameters of comparison between LDPC and Turbo codes

	LDPC	Turbo
Modulation	BPSK	BPSK
Coding	Rate-1/2, block length 512-bit	Rate-1/2, block length 512-bit
No of Iterations	25	2
SNR (dB)	[0 : 3.7]	[ 0 : 3.7]
Channel estimation	Gaussian channel	Gaussian channel
Input image	Cameraman 256×256	Cameraman 256×256

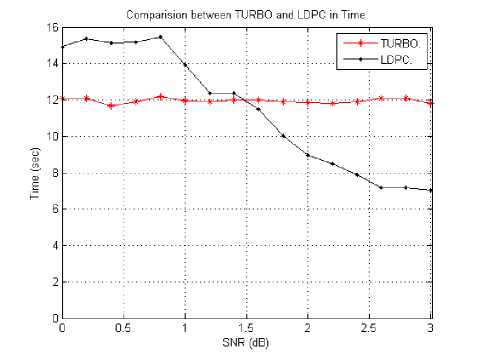
Fig. 4. Time versus SNR of the received cameraman image with Turbo and LDPC

From the previous figure 3 and 4 it is clear LDPC has a small BER than turbo codes and it executes short time with LDPC at SNR from 1.5 to 3 compared to Turbo code so that it preferable to use LDPC as an error correction code in our proposed scheme.

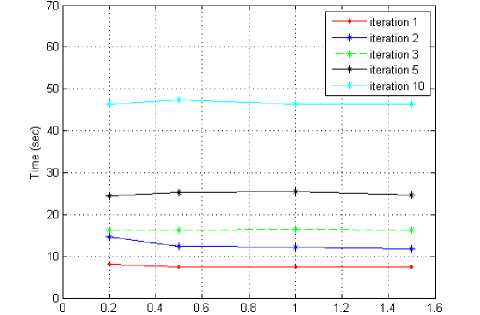
We can improve the performance of turbo code by making some increase number of iterations and decreasing block length that will improve the performance, where these conditions executed long time and it is not suitable for real time application in an image as can be shown in the figures 5 and 6.

We study the effect of the number of iterations by taking SNR to be changed from 0.2 to 1.5 as sample of noise, and testing the BER and the execution time for correcting the errors. It is clear the performance of turbo code depends mainly on the number of iterations and does not depend on the value of the SNR.

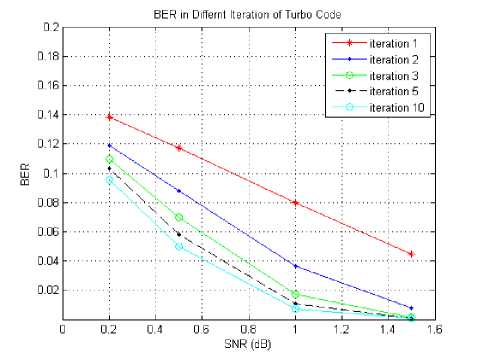
Fig. 5. SNR versus BER of the received Cameraman image with different iteration in Turbo codes

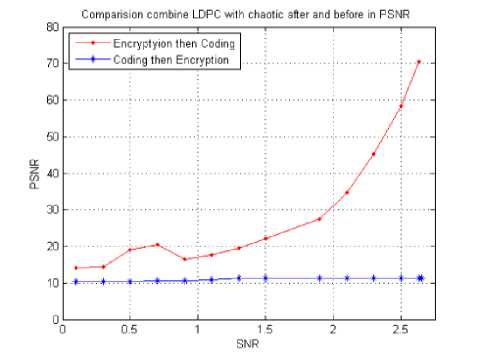
Fig. 7. PSNR for combining encryption with LDPC coding after and before for various SNRs (dB).

Comparision combine LDPC with chaotic after and before in Time

SNR (dB)

Fig. 6. Processing time at different iteration in Turbo codes

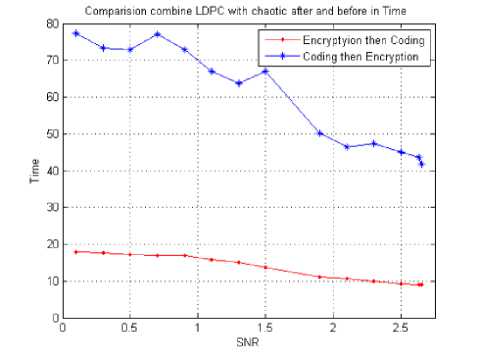
Fig. 8. Processing time for combining encryption with LDPC coding after and before for various SNRs (dB).

• IV.    Procedure Of Combining Encryption With Coding

The encryption and LDPC algorithms are applied in two different methods; first we applied coding, then encryption as follows: we first applied encoding the original image (cameraman.bmp) using LDPC then applied encryption using the Arnold cat map as the type of encryption [17], we use BPSK for modulation and AWGN as a channel. The second method is using the same algorithm but in this case we applied the encryption first, then coding. At the destination, we applied decode, then decrypted the decoded image. We compare between the two methods by measuring BER, FER, PSNR and processing time. The simulation results of the two methods can be shown in the following figures7, 8, 9 and 10.

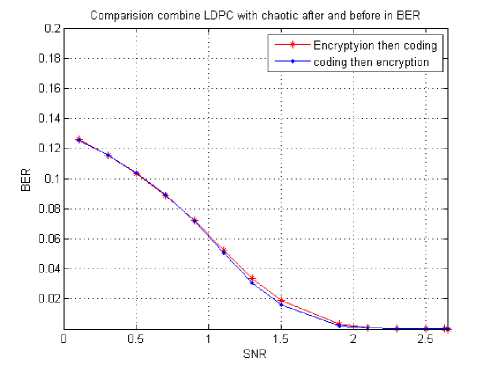
Fig 9. BER for combining encryption with LDPC coding after and before

From the previous figures 7, 8, 9 and 10 we can conclude that:

• 1-    By measuring the parameter PSNR, as can be shown in figure 7, it is evident that applying encryption, then coding gives better results in the reconstruction of the decoded decrypted image.

• 2-    There are small improvements in BER and FER by applying coding then encryption, as is clear from figures 8 and 9.

• 3-    The performance of applying encryption then coding has smaller execution time compared to the time executed by applying coding then encryption. That is due to the fact that in the coding then encryption, we encrypt the parity which is added to the image in encoding the image. So combining encryption with coding is preferable to apply encryption and then coding.

• V.    Combination Of Hybrid Chaotic Encryption And Ldpc Code

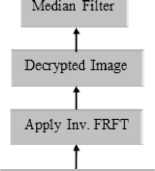
We proposed a new schema which combines encryption and then coding in one algorithm. We use a hybrid chaotic system as follow: first an image is transformed to the fractional Fourier transform domain [14]. Secondly, the transformed image is encrypted using two stage encryption scheme of confusion and diffusion presented by Arnold Cat map for confusion and proposed Hénon map3 for diffusion [14]. Finally the encrypted image is obtained. More details about this algorithm are shown in [14]. We combine this encryption algorithm with LDPC codes for channel coding as shown of flowchart of figure 11. The encoded encrypted image is then modulated by Binary Phase Shift Keying (BPSK), transmission over channel Additive white Gaussian noise (AWGN), which is considered in our simulation. AWGN is a basic noise model used in information theory to mimic the effect of many random processes that occur in nature. At the receiver side, the received image was demodulated, decoded and decrypted. After decryption, we will pass the image through a median filtering to reduce noise.

We compare our proposed algorithm by combining LDPC code with three different algorithms. First applying RC6 [15], second applying Baker chaotic map [16], and finally applying LDPC without encryption. We compare among all these algorithms in tests for BER, FER, and PSNR. We will carry out a comparison between the image transmission using this proposed scheme and the transmission of the original image using the previous algorithms. We compare between them to determine the performance of our proposed scheme and measure the ability for secure image transmission and error correction in the noisy channel.

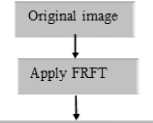
Confusion algorithm Arnold Cat map

Confusion algorithm Arnold Cat map

Diffusion algorithm Henon map 3

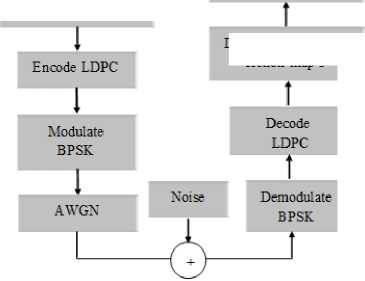
Fig. 11. Combination of hybrid chaotic map with LDPC code in a Shannon channel

Diffusion Algorithm Henon map 3

• VI.    Experemental Results

The performance of the combination between hybrid chaotic map and LDPC channel coding for image transmission through AWGN channel has been demonstrated under the simulation parameters shown in Table 2.

Table 2 Simulation parameters of proposed scheme

Modulation	BPSK modulation
Coding	LDPC coding Code rate = 1/2 Block length 512-bit No of Iterations = 25
SNR (dB)	From 0 to 2.75
Channel	AWGN channel
Filter	Median filter
Ciphering	Hybrid chaotic encryption using FRFT

We combine three different image encryption algorithms with LDPC to decide on the best of them. First we combine Baker chaotic map with LDPC code [16]. Second, combine RC6 with LDPC code [15]. Third apply LDPC without encryption; finally our proposed algorithm hybrid chaotic map using FRFT [14] combined with LDPC code. We make comparisons among all these algorithms in some tests as BER, FER, and PSNR. The result of the combination of different encryption and LDPC can be shown in the following tables and figures.

Table 3 PSNR for different encryption models combine with LDPC

SNR	Without encryption	Chaotic	RC6	Proposed hybrid chaotic map using FRFT
0	13.92	13.56	13.55	13.57
0.5	14.84	14.56	14.58	14.57
1	17.11	16.87	16.90	16.89
1.5	23.00	23.19	22.83	23.00
2	34.72	34.99	34.70	35.54
2.5	49.94	52.96	53.91	65.26
2.75	∞	72.47	72.42	72.42

Table 5 BER for different encryption models combine with LDPC

SNR	Without encryption	Chaotic	RC6	Proposed hybrid chaotic map using FRFT
0	0.13069	0.1304	0.13035	0.13015
0.5	0.10399	0.1037	0.10338	0.10346
1	0.06082	0.0606	0.060712	0.060706
1.5	0.01555	0.0142	0.015591	0.014794
2	0.00109	0.00097	0.000993	0.000866
2.5	3.29e-5	1.52e-5	1.57e-5	9.53e-7
2.75	0	0	0	0

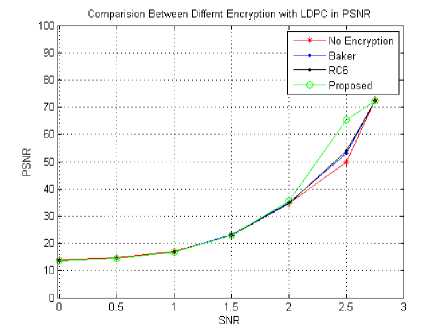
Fig. 12. PSNR vs. SNR for combining different encryption models with LDPC

• A.    Peak Signal to Noise Ratio

Table 3 and figure 12 show the PSNR against BER. Which are the measurements of the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. PSNR values are measured Appling four models for the combination of Hybrid chaotic and LDPC coding for various Signal to Noise Ratios (SNRs) of the received cameraman image. The higher PSNR for the proposed scheme indicates more efficient system performance.

Table 4 FER for different encryption models with LDPC

SNR	Without encryption	Chaotic	RC6	Proposed hybrid chaotic map using FRFT
0	1	1	0.9997	0.9997
0.5	0.9877	0.9856	0.9814	0.9824
1	0.7417	0.7434	0.7385	0.7441
1.5	0.2263	0.2089	0.2270	0.2187
2	0.02002	0.0168	0.0166	0.0151
2.5	0.00073	0.00024	0.00048	0.00024
2.75	0	0	0.00024	0

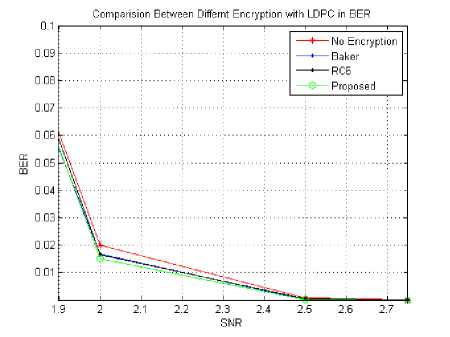
Fig. 13. BER for combining different encryption models with LDPC

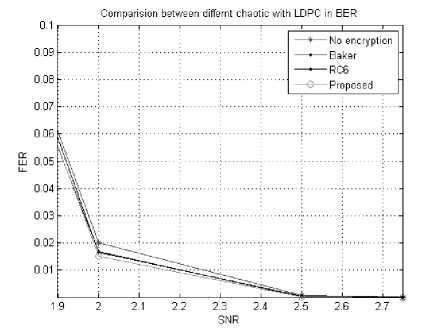
Fig. 14. FER for combining different encryption models with LDPC

• B.    Bit Error Rate and Frame Error Rate

Tables 4, 5 and figures13 and 14 illustrate the BER and FER versus SNR respectively. BER and FER are computed after decoding, as a function of signal to noise ratio. BER and FER are measured for four models of combination of Hybrid chaotic and LDPC code for various SNRs. It is clear that the proposed scheme has very a small value of the BER and FER at small SNR so that it has better error performance.

From the previous figures and tables it is clear that our proposed algorithm with LDPC gives the best results compared with RC6, Baker and the original image without encryption.

• C.    Histogram Analysis

The original image can be shown in figure 15, the histogram of the original image and its encrypted image using a hybrid chaotic map is given in Figure 16 and 17. These figures show that the histogram of the encrypted image is fairly uniform and completely different from that of the original image.

Fig. 15. Original Cameraman Image

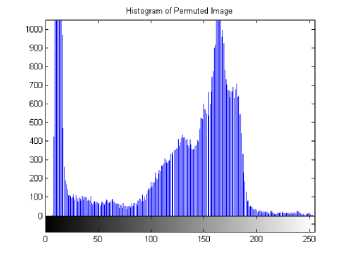
Fig. 16. histogram of original image

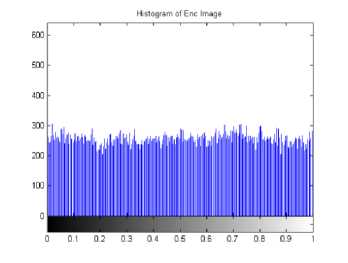
Fig. 17. Histogram of encrypted image

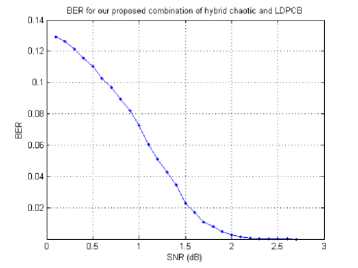
Fig. 18. BER vs. SNR of the received image combination of hybrid chaotic encryption and LDPC

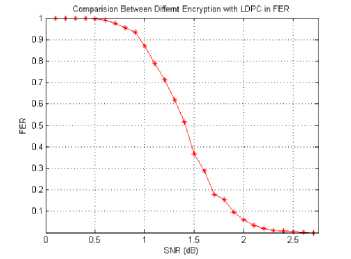
Fig. 19. FER vs. SNR of the received Cameraman image with combination hybrid chaotic and LDPC

The following figures are produced from applying our proposed algorithm to secure transmission of the image besides error correction. We show the ability of the algorithm to correct the errors at different SNRs

We introduce the performance analysis of our proposed algorithm to secure transmission of image through a noisy channel by drawing the following three figures, which measure the BER FER and processing time. It is clear that our proposed algorithm gives very small BER at small SNR and it has also high PSNR at small SNR. It executes at a short time when applying encryption, encoding, decoding and decryption of image all these algorithms execute in 14.55 sec at SNR = 2. Also, it can reconstruct the decoded decrypted image as the original image with noisy channel, besides, it could secure the transmission image as it clear from the histogram of the encrypted image in figure 17.

Fig. 21. Reconstructing image at SNR=2 dB

Fig. 20.Reconstructing image at SNR=1 dB

Fig. 22. Reconstructing image at SNR=2 dB using median filter

Fig. 23. Reconstructing image at SNR=2.5 dB image besides error correction

Figures 20, 21, 22 and 23 give the reconstructed image of the proposed scheme at different values of SNR over AWGN channels. As shown a small change in SNR yields high quality in the reconstructed image.

It is observed that in the case of the reconstructed image for a channel with SNR = 1, 2, 2.5 dB with the combination of hybrid chaotic map and LDPC coding, it is possible to reconstruct the image clearly with the combination of LDPC coding, and the image is reconstructed without distortion. we don't need to retransmission of image when it noisy therefore our proposed algorithm increases the throughput of the system. The use of median filter on the receiver side improves the reconstruction of the image in the presence of noise as is clear in figure 22.Our proposed scheme is effective for secure image communication over the wireless noisy channel.

• VII. Conclusion

In this paper, we proposed a scheme for the combination of image encryption and error correction code. The proposed scheme combines image encryption based on hybrid chaotic encryption, and error control coding based on LDPC channel coding. Simulation results show that the proposed scheme enhanced the performance parameters and achieved both security and reliability of image transmission through the wireless channel. The proposed scheme is suggested for secure image transmission over wireless channels. It proposes to apply encryption before coding because of shorter execution time than when applying coding, prior to encryption; besides, it gives good result in the reconstruction of the image at the receiver side. Also as is evident from the results in this paper, LDPC gives better results than Turbo code. Our proposed scheme yields better results than RC6, Baker map and without encryption. Finally we can conclude that our proposed scheme is very effective for secure image communication over wireless noisy channels. Further works is needed for developing an optimization scheme for the security issues and error correction code for wireless image transmission.