Common Fixed Points of Self Maps Satisfying an Integral Type Contractive Condition in Intuionistic Fuzzy Metric Space
Автор: Saurabh Manro
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 5 vol.4, 2012 года.
Бесплатный доступ
In this paper, we prove two common fixed point theorems. In first theorem, we prove common fixed point theorem for two weakly compatible self maps of type (A) satisfying an integral type contractive condition in intuitionistic fuzzy metric space. In the second theorem, we prove common fixed point theorem for two weakly compatible maps satisfying an integral type contractive condition in intuitionistic fuzzy metric space. These results are proved without exploiting the notion of continuity and without imposing any condition of t-norm and t-conorm.
Intuitionistic fuzzy metric space, weakly compatible maps, weakly compatible maps of type (A), common fixed point
Короткий адрес: https://sciup.org/15010703
IDR: 15010703
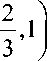
Список литературы Common Fixed Points of Self Maps Satisfying an Integral Type Contractive Condition in Intuionistic Fuzzy Metric Space
- K. Atanassov, Intuitionistic Fuzzy sets, Fuzzy sets and system, 20, 1986, pp. 87-96.
- J. H. Park, Intuitionistic fuzzy metric spaces, Chaos, Solitons & Fractals, 22, 2004 pp. 1039- 1046.
- C. Alaca, D. Turkoglu, and C. Yildiz, Fixed points in Intuitionistic fuzzy metric spaces, Chaos, Solitons & Fractals, 29, 2006, pp. 1073-1078.
- I. Kramosil and J. Michalek, Fuzzy metric and Statistical metric spaces, Kybernetica, 11, 1975, pp. 326-334.
- D. Turkoglu, C. Alaca and C. Yildiz, Compatible maps and Compatible maps of type and in intuitionistic fuzzy metric spaces, Demonstratio Math., 39, No.3, 2006, pp. 671-684.
- G. Jungck, Commuting mappings and fixed points, Amer. Math. Monthly, 83,1976, pp. 261-263.
- B. Schweizer and A. Sklar, Probabilistic Metric Spaces, Morth Holland Amsterdam,1983.
- G. Jungck, BE Rhoades, Fixed point for set valued functions without continuity, Indian J Pure Appl Math, 29, No.3, 1998, pp. 227-238.
