Comparative Analysis of Customers' Queue Management of First Bank Plc. and Guaranty Trust Bank Plc, Isokun Ilesa, Nigeria

Queuing theory which is a branch of operation research often used in making decision about resources needed to provide service. It has applications in wide varieties of situation that may be encountered in business, commerce, industries, healthcare, public services and engineering. In particular, queue theory is very useful in customer services situations as well as transportation and telecommunication. Application is also found in intelligent transportation system, business core center, network environment, server queuing mainframe, computer and traffic flow.

Queuing is a volatile situation in establishment. A part form time wasted, it also leads to break down of law

* Corresponding author – Rogushina Julia.

and order. Cases of loss of lives were reported at filling stations in the years of fuel shortage or scarcity in most part of the world especially in Nigeria.

Queuing wherever it occurs has many negative consequences a part form leading to chaos for instance, Baking industries, wasting of man hours per cases have been witnessed where customers while waiting to cash money are attached by armed robbers. And many times the robbers are made away with huge amount of money from people on the queue in banking halls and even kill or injure some of them. Unhealthy people develop complications while waiting, this sometimes leads to death if proper medication is not provided.

In recent times, in banking sector in Nigeria, many new generation banks were licensed with a view of reducing congestion often experienced in the old generation banks. Despite all these, there is queuing problem in some of these banks. It is therefore necessary to carry out appraisal performances of the available banks.

In this study, we want to find out if licensing new generation banks will solve the problem of long queues in Nigerian banks and therefore compare the efficiencies of the old generation banks with the new generation banks.

• 2.    Related Works

Queue theory can be used to analyze more abstract queues such as in operating system design, saving and withdrawals of cash in banks. It is used to increase placement of merchandising materials at the same time alleviating the actual amount of time a customer spends on waiting line.

Erlang, a Danish Engineer who is called the father of queue theory published a paper that narrated the study of congestion in telephone traffic [1]. Molina in [2], worked on theory of probability of telephone trekking problems. Pollaezek (1930) did some works on poison input with single multiple channels problems [3]. Jackson (1957) presented a paper on network of queue where a customer was to go for more than one service point [4]. Little (1961) also joined the group researchers on queuing theory, when he developed a relationship between the expected numbers of customers on the queue in a steady state [5].

A review on the positive correlation between arrival rate of customers and banks service rate was carried out in [6] while in [7], it was researched that if service system could provide service at faster rate than customers’ arrival rate, waiting line could still be formed if the arrival and service process are random. Posner and Bernholtz in 1968 treated closed to Jackson networks but, allowed ample service travel time nodes with general travel time (holding time) distribution. They showed that if one were interested in only one marginal probability distribution of a steady-state system size at set of rodes, exclusive of the travel time rode, the exact form of the travel distribution did not matter [8].

In [9], multiple-class queuing systems with N-policy in which the idle server starts service as soon as the number of customers in the “start-up” reaches threshold N. The work considered cases of first come first served and no preemptive priority. They obtained the Laplace-Stieltjes transform of the waiting times of each class of customers. They also showed results for general behavior of such systems in their study.

• [10]    deals with the policy for the M/G/1 queue and [11], with the M/G/1 queue with D-policy, i.e., the server is turned off at the end of a busy period and turned on when the cumulative amount of work firstly exceeds some fixed value D. In the work, it was firstly concentrated on the computation of the steady-state probabilities. The first moments and relationships among the busy period, the number of customers served and other performance measures are investigated. Some variants of the main model and the special case of the M/M/1 were also studied.

• 3.    Methodology

• 3.1.    Model Specification

A MX/G/1 queuing system with N-policy was considered in [12]. In the study, the server is turned off as soon as the system empties. When the queue length reaches or exceeds a predetermined value N (a threshold), the server is turned on and begins to serve the customers. In the study, they placed emphasis on understanding the operational characteristics of the queuing system. One of their findings was that the system size was the sum of two independent random variables: one has the PGF of the stationary system size of the MX/G/1 queuing system without N-policy and the other one has the probability generating function. [13]. divide the companies' customers into different priority groups to be served according to their payment history and feedback in order to increase the companies' performance and profit and save the time of customers within high priority class which may lead to increase their satisfaction. [14]. Worked on new model for call center queue management. [15]. Compares three Active Queue Management (AQM) methods, namely, Adaptive Gentle Random Early Detection (Adaptive GRED), Random Early Dynamic Detection (REDD), and GRED Linear analytical model with respect to different performance measures.

This section considers the materials, statistical models and methods used in the study and they are logically grouped below:

This model deals with situation where there is more than one service station in parallel where any station can serve customer on the waiting line.

Where, e= traffic intensity

µ= service rate of the number of people serviced per unit time л= average arrival rate of the number of people arriving per unit time

C= the number of servers (cashiers)

The probability of having no customer in the queue:

с! (1 - e)

P0 =---------------------

(^ + С!(1-е)У ОСес)"

The probability of not queuing on arrival is given as:

₌ (ec)^cp₀

The average number of customer in the system is given as:

_ e^ecypo + ec

The average number of customer in the queue:

_ e(ecypo

The average time a customer spends in system:

t _ e(ec)c *Po +(6)

C!(l—e)2C/z       n'

The average time spent in queen:

W =

С! (1 — е)2сц(7)

• 3.2.    Linear Markovian Birth Process

In linear Markovian pure birth process: the probability of birth in a small time interval is proportional to the current number of population and the length of interval. That is for all n:

Д„ = 0 and Дп =.

The constant proportionality is birth rate or arrival rate:

pn = /(l-e-At)n-VAt

The expected size of the population at time t:

E [(^)t]=e   t if the population is initialized with members, then size at time t is (E [(/^)t]=e)

• 3.3.    Application of Queue Model

Table 1. FIRST BANK Plc. With C=3 (i.e. number of cashiers)

S/N	No of arrival	A	Departure
1.	54	0.9	56	0.93
2.	56	0.93	59	0.98
3.	61	1.02	62	1.03
4.	58	0.97	61	1.02
5.	62	1.03	65	1.08
6.	59	0.98	63	1.05
7.	61	1.02	64	1.07
8.	60	1.00	62	1.03
9.	56	0.93	59	0.98
10.	55	0.92	60	1.00
11.	54	0.90	56	0.93
12.	57	0.95	58	097
13.	62	1.03	63	1.05
14.	60	1.00	62	1.03
15.	61	1.02	63	1.05
16.	58	0.97	65	1.08
17.	58	0.97	64	1.07
18.	63	1.05	64	1.07
19.	53	0.88	56	0.93
20.	56	0.93	62	1.03
21.	58	0.97	63	1.05
Total	1222		1287

The data used in this research work is primary data and the method of data collection is through observation. The number of customers serviced in 60minutes in each day was observed and recorded. The number of arrival is the number of customers serviced described earlier added to the number of customers still on the queue at the end of 60minutes.

Average Arrival Rate— = 58.19

Average Arrival Rate Я = 58.19

• -х 60 =   ¹ х 60 =1.03 minutes.

Л          58.19

Average Service Rate ------ 61.29

д = 61.29

Average Service Time = -X — = 0.98 minutes и 1

Traffic Intensity = е = —

СЦ

С = 3,Л = 58.19,ц - 61.29

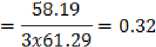
The probability of having no customer in the system:

Р_о=_________ d(i-e) _________

(^^([-^^(п-Хес)-

3! (1 - е) (Зх0.32)³ + 3!(1- O.32)(q7 (0.3x3)°+ ^(0.32x3)! l^j (0.03х2)² = 0.41

Probability of queuing on arrival:

т (есУр°

С’.(1-е)

(0.32хЗ)3 3! (1 - 0.32)

хО.41 = 0.089

Probability of queuing on arrival:

(ecYp°

1         = 1 -0.089 = 0.91

C’.(i-e)

The average number of customer in the system:

е(ес)^ср₀ + ес

C'(i-e)2

0.32 (0.32x3) 310.41 +0.3213 3!(1—0.32)2

= 0.042 + 0.96 = 1.0

That is, 1 customer / minute.

Average number of customer in the queue:

е^УГо

C! (i - e)2

0.32(0.32i)3i0.41

----;-------+7— = 0.04 31(1 - 0.32)²

Average time spent in the system:

(ecy , 1

c!(l -e^Cp ~^{Po +} p

(0.3213)3                 1

---------—— 0.41+--- 3!(1- 0.32)23x^^       61.|

= 0.0168 + 0.39 = 0.41/lour

=24.41 minutes

Average time spent in the queue:

(ec)p₀         (0.32x3)³x0.41

c!(l-e)²C^ ~ 3!(1 -0.32)x3x61.29

= 0.017 hours = 1.03minutes

Linear Markovian Birth Arrival process expected size of the queue or population the banking hall in 2hours if the population is initialized with one member:

E^-N^EK^Ixe^'1^^

127.6 ~ 128ro5tomer

Table 2. GTB Plc. With C=6 (i.e. number of cashiers)

S/N	ARRIVAL /HRS	Л	DEPARTURE	µ
1.	105	1.75	177	1.95
2.	103	1.72	133	1.88
3.	113	1.88	119	1.98
4.	117	1.95	123	2.05
5.	123	2.05	129	2.15
6.	119	1.98	125	2.08
7.	115	1.92	123	2.05
8.	101	1.68	121	2.02
9.	113	1.88	125	2.08
10.	117	1.95	129	2.15
11.	121	2.02	133	2.22
12.	115	1.92	127	2.12
13.	103	1.72	119	1.98
14.	105	1.75	121	2.01
15.	117	1.95	129	2.15
16.	119	1.98	135	2.25
17.	117	1.95	133	2.22
18.	113	1.88	129	2.15
19.	107	1.78	127	2.12
20.	103	1.72	121	2.02
21.	101	1.68	113	188
Total	2347			2611

2347       _

Average Arrival Rate =----= 111.76

ы                 21

Л - 11.72

1 customer arrive on the queue

Л

60 =----- x 60

111.76

0.54minutes or 32.21 seconds 2611

Average Service Rate =---- = 124.33

y                 21

g = 124.33

_        1

Average Service Time = — x 60

24.36

•minutes x 60 = 0048-------

28.75sec

_                      111.76

Traffic Intensify e = ---= 0.15.

1     6x124.33

The probability of having no customer in the system:

Р_п_ _________ С!у-в) _________

*               ТчП—С~

(«^ЧС!(/-вК>    ^“^

= 61(1-0.150)

(6il50)6+6! (1 - 0.0150)(l/0! (61150)”+jy (6x0.150)1 + ^ (6i0.150)!5! (M.150)5

Ро=О.4О7

Probability of queuing on arrival:

(есУр₀ (6х0.150)⁶х0.407 с! (1-е)^-  61(1-0.150)

= 0.00035

Probability of not queuing on arrival:

(ес)ср0

1 ------------- с! (1 — е)

0.0003 5 - 0.999

Average number of customer in the system:

(есУро , с!(1-е)²

0.150(0.150x6)6x0.407 + 0.150x6

61(1 - 0.150 У

= 0.90~1 customer

Average number of customer in the queue:

У^есУРо с! (1-е)²

0.150(0.150x6)6х0.407

6!(1 - 0.377) = 0.00012

Average time spent in the system:

(ес)с          1

с!(1 — еуСрР° р

(0.150хб)6х0.407 + 124 зз/24

6!(

= 0.19/iours = ll.SSminutes

Average time spent in the queue:

МсРо с! (1 - 0.150)26х124.33 = 0.00001

Linear Markonau birth/arrival process the expected size of the queue or the population on the queue or the population in the banking hall in 2hours per day is initialized one member:

E(N)(t) = IV^Je^ = 1ле^^11,761—) = 11.085 customer

• 3.4.    Result

  The analysis shows an important result which interprets as follows: The number of customers arrived at that time was greater than the number of the cashiers. The probability of queuing on arrival in First Bank was 0.089 and Guaranty Trust Bank was 0.00035. These are weak probability but it is still possible for customer to wait before receiving services. The average number of customers waiting to be served in First Bank Plc. was one customer per minute while Guaranty Trust Bank Plc. was one customer per minute which means at time there will be no customer in the queue.

• 4.    Conclusions

Average time spent in the system in First Bank was 24.41 minutes and average time spent in the queue was 1.03minutes which means that a customer spent at least 23.38minutes in the queue.

Guaranty Trust Bank, average time spent in the system was 11.52 minutes which is shorter than that of first bank. Lastly, if the time is extended to two hours in a day First Bank has 128 customers and Guaranty Trust Bank will have 11,085 customers to be attended to.

A multi-channel queue model was used to analyse the data. The following were calculated with queue model:

The probability of having no customer on the queue for two banks, the probability of not queuing in the system for two banks, the average number of customer in the system for two banks and the average time spent in the queue for the two banks.

The Markovian birth process was used for the two banks and the result from the analysis shows that new generation bank is more efficient than old generation bank. Some people believe some much in old generation banks because of fear of liquidation and few other reasons, therefore, the increased patronage make them less efficient because management fails to increase their servers.

Secondly, the two banks are efficient for the fact that probability of queuing on arrival is not up to 0.1minute. This means that if customer will queue at all, it will be for a very short period of time. The average number of customers waiting to be served in all the banks is not up to one, which means no customer is waiting for service. The best bank is determined by the average time spent in the system and the expected queue is extended to two hours per day. The more efficient bank is guaranty trust bank which has a maximum of 11.53 minutes as average time spent in the system and 11,085 customers on the queue if the hours are extended to two hours and this customer is expected to be attended to within 12minutes. The management of First Bank needs to improve their service mechanism because most of time spent in the banking hall is used in receiving services. This at times is beyond human effort because is mostly caused by online services. Server may go down or poor network services of automated teller machines. First Bank may need to employ more cashiers to be more efficient

Acknowledgment

We wish to acknowledge the supervisor of this work, Dr. Tope Omolofe and all other fellows who in one form or the other assisted in a successful execution of the work.