Comparative analysis of reflection symmetry detection methods in binary raster images with skeletal and contour representations

Symmetry detection in binary raster images is a well-known problem; there are robust approximate and exact methods [1–11]. However, comparative studies of their quality and performance are virtually not available.

This study compares two reflection (mirror) symmetry axis detection methods: an algorithm to refine the symmetry axis found with chains of skeletal primitives alignment [1, 2], and a contour method based on the Fourier descriptor [3].

The reference for quality assessment is the result of the exact reflection symmetry axis detection algorithm based on Jaccard’s measure [4]:

IS ( B ) П S ( Br )|

^Ц T ⁽ B) S ( B ) о S ( В , )Г ⁽¹⁾

where B is the binary image, the brightness values are either 1 for black pixels or 0 for the white pixels; B r is a mirror reflection of the original binary image B relative to a straight line, S ( B ) is a set of the image B pixels with their brightness level=1. Obviously, ц _T ( B ) = 1 has more favorable basic measure properties: 0 <ц _T ( B ) <  1, while ц T ( B ) = 1, if B is perfectly symmetric, and ц _T ( B ) = 0, if B and B r do not intersect. The measure (1) for binary images (vectors) is called a Tanimoto similarity in some sources.

To find the intersection and union of the sets of pixels of the original image and the reflected one, it is first necessary to get a mirror reflected image. Let's derive an analytical expression for obtaining a mirror reflected image B r of the original binary image B , relative to a straight line given by a pair of points ( x 1 , y 1 ) and ( x 2 , y 2 ). The axis relative to which the mirror reflection is performed is given by an equation of the form f ( x ) = kx + b , where the coefficients k and b are obtained as follows:

k _ y!--y ¹ ; b _ y 1 _ kx 1 .

x 2 _ x 1

Note that k = tg ф = (sin ф /cos ф ), where ф - is the angle between the straight line and the axis Ox . Let's express cos ф and sin ф from here as follows:

cosф_ ------= -----, sin ф_ tg ф cos ф_ k cos ф .

\ 1 + tg 2ф \1 + k2

To do this, we use a group of affine transformations in the following order:

• 1)    the offset of the image along the axis Oy by a factor b to the origin;

• 2)    rotation of the image by an angle л / 2 - ф (the angle between the straight line and the axis Oy );

• 3)    performing the mirror reflection operation along the axis Oy ;

• 4)    performing the operation reverse to the operation 2;

• 5)    performing the operation reverse to the operation 1.

Then the combined matrix of these affine transformations will be the following:

cos² ф_ sin² ф   2cos ф sin ф      _ 2b cos ф sin ф

2cos ф sin ф sin² ф_ cos² ф b ( 1 + cos² ф_ sin² ф )

Applying this affine transformation to the original image, we get an image that is a mirror image of the original one. Obviously, the affine transformation will translate integer pixel coordinate values into real-valued ones. In this paper, we use a threshold (rounding rule) when calculating the coordinates of a new pixel, which of course affects the accuracy of the methods for working with a raster image. We conducted a study to evaluate the impact of this rounding rule. The essence of the experiment is that we estimate the Jaccard measure for an image re- flected relative to a random straight line and then reflected relative to the same straight line "back". Thus, with each double reflection, we get "kind of" a new copy of the image but subjected to an affine real-valued transformation. We repeated this procedure for one hundred random lines and recorded the obtained Jaccard measures. Fig. 1 shows one hundred obtained values, sorted in ascending order. As it is seen, the corresponding residuals (differences from the value 1) do not exceed 0.003, which is, apparently, the natural accuracy of the method.

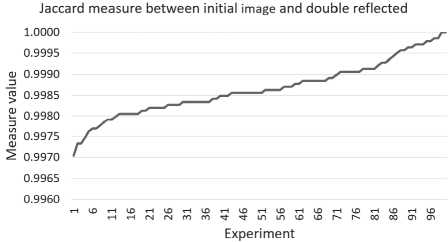
Fig. 1. Jaccard measure between initial image and its double reflected copy for 100 random axes

The exact reflection symmetry detection algorithm enumerates every line intersecting the figure defined by its boundary points and finds the one with the max symmetry measure (1). This line is the image’s reference axis of symmetry. The symmetry measures for the reference axis in real-world applications (e.g., scanned plant leaves, binarized ROIs in digital photographs) rarely reach 1. We will call an image quasi-symmetric if its measure (1) is close to 1. Fig. 2 shows axes and their symmetry measures for ideal, quasi-symmetric, and asymmetric images.

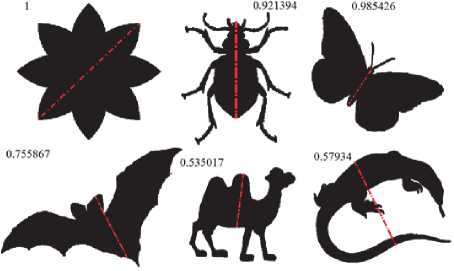
Fig. 2. Image examples. The axis corresponds to the max symmetry measure estimates with Jaccard similarity

Since the computational complexity of the exact algorithm is considerable, several better performance options were proposed, as well as fast approximate methods, the algorithms to refine the symmetry axis found by comparing the subchains of skeletal primitives alignment [1, 2]. In this paper, we use a parallelized version of the exact algorithm [5]. Problem statement: comparison of the two reflection symmetry axis detection algorithms in terms of accuracy and performance relative to the reference solution. The measure of accuracy is Jaccard’s measure.

Review of available reflection symmetry detection methods applicable to binary raster images

The symmetry axis detection and two-dimensional shape symmetry estimation problems are well known. There are many efficient solutions based on: 1. parametric representation of the shape contour and its Fourier transformation [6], 2. contour representation with rotation [7], 3. representation of the contour by critical points and estimating the similarity measure for two sub-boundaries using geodesic distance vectors [8], 4. the electric charge distribution model (ECDS) [9], 5. the contour-skeleton function (BSF) [10], 6. pairwise comparison of skeletal primitive subchains [1], 7. building the Fourier descriptor of the image contour [3], 8. building image gradient histograms [11], 9. a descriptor built on the Radon transform [12].

An exact algorithm was proposed in [1] to evaluate and compare the binary images reflection symmetry detection algorithms. It detects the reference quasisymmetry axis and the measure of image symmetry. The exact algorithm performance is low; it cannot process images in real-time or close to real-time. Paper [1] proposes its optimization options, while [5] presents a parallelized, supercomputer-ready version.

Axis position refinement algorithm based on the skeletal primitive subchains alignment

The refinement algorithm concept is to use a fast approximate method first and then improve its results. Paper [1] shows that the method based on skeletal primitive subchains alignment is a fast approximate method for reflection symmetry axis detection. Compared to complete enumeration (CE) and even to its optimized versions, the skeletal method is much faster. The initial axis it produces is approximate. We should find the axis in its vicinity with the highest Jaccard’s measure. For this, the axis is slightly shifted ("swings") across the shape. Paper [2] covers three refinement algorithm options. This paper uses a parallelized version of the second refinement algorithm option since it offers the best performance, accuracy, and predictability of the result [5]. Its essence is as follows. The initial axis crosses the shape contour at two points. We define points within a given neighborhood of the contour e : they represent two finite sets of some points on the contour, which are the search intervals. Then we define n equidistant points on each interval. The points in the two intervals are enumerated in pairs forming several test lines; the one with the maximum symmetry measure is chosen. The algorithm is repeated with the new line and a reduced interval until the interval reaches 1. Also, for each test axis, we check if it is in the vicinity of the center of mass (CoM). This eliminates some of the lines from the search and accelerates the algorithm. As a result, we find the axis with the measure of symmetry is not be less than the measure produced by the skeletal method.

This algorithm is intrinsically paralleled associated as we enumerate all the test lines in the specified neighbor- hood and estimate their symmetry measure values. These operations are independent and can be performed in parallel for different lines. Parallel computing will further improve performance.

Contour method based on the Fourier descriptor

Paper [3] presents a method based on the Fourier descriptor applied to the image contour as an alternative to other methods with high computational complexity. The contour method is as follows. The shape’s contour points are represented by a sequence of complex numbers, where the real is the x coordinate and the imaginary part is the y coordinate. The discrete Fourier transform is then applied to the sequence of points. The resulting coefficients are called the Fourier descriptor of the image contour.

To find the symmetry axis, we should enumerate all the points of the contour and for each point find the optimal line dividing the contour into two similar parts. To determine the line quality, the Q measure is used. It is the standard deviation of the coefficients from the optimal axis for all possible cyclic shifts of the contour. The closer Q is to 0, the closer the line to the true axis of symmetry. The measure Q characterizes the shape asymmetry. Its range is [0, + ^ ]. It is assumed that the shape is symmetric if Q does not exceed an empirically defined threshold.

This paper assumes that the shape’s symmetry axis is always the symmetry axis of the convex hull of the given shape. The symmetry axis may contain either a point being a vertex of the convex shell or a point that lies on the line passing through the center of gravity and the center of the convex hull edge. To improve the performance, the convex shell points and the small neighborhood around these points are examined. However, it is worth noting that in the general case this assumption is not met.

Also, not all of the Fourier descriptor coefficients are required to describe the shape with sufficient accuracy, but only those with a sufficiently large absolute value. Usually, these are the first and last harmonics. To improve the performance, some of the Fourier coefficients are discarded (only coefficients that are greater than some manually defined threshold in absolute values). The procedure is equivalent to a contour frequency filtering to approximately detect the symmetry axis.

To calculate the exact measure of the asymmetry of the shape Q the full set of coefficients in the small neighborhood of the found vertex is estimated.

Experiments

The FLAVIA binary raster image database was used for experimental studies [13]. The FLAVIA database contains 32 classes of leaf images approx. 800x600 pixels (see fig. 3).

Fig. 3. Example: images of 32 leaf classes from the FLAVIA database

Classes 3, 4, 5, 10, 12, 16, and 21 were selected. The images were processed by the exact CE algorithm, the reference axis of symmetry was found for each image, and Jaccard’s measure of symmetry J (1) was estimated. For each class, the best symmetry axes and their corresponding symmetry measures Ja were obtained by aligning skeleton primitives subchains (the axis refinement algorithm). The images were also processed by the contour method based on the Fourier descriptor. The best symmetry axis, asymmetry measure Q were obtained for each image, and Jaccard’s measure Jq was calculated for the ob- tained axis. Since the algorithm finds several symmetry axes based on the Fourier descriptor, in this experiment we chose the axis with the smallest asymmetry measure Q.

The algorithms were implemented as C++ codes. An accurate CE algorithm processed images using 128 threads on the Lomonosov supercomputer [14]. The refinement algorithm for the initial axis found by aligning skeleton primitives subchains was run in 2 threads. The search intervals were divided into 10 segments, the CoM neighborhood was equal to 3 % of the distance between the CoM and the farthest point on the contour.

The accuracy and processing time for various leaf image classes obtained by the two algorithms are summarized in tab. 1. The following properties were estimated for each class: the average value, RMS, min and max values. The Jaccard measure for the axes found by the approximate methods always either does not exceed or at best equals the measure obtained by the exact CE algorithm. Let us estimate how close the proposed fast algorithm results are to the reference result. The best time and accuracy values for the two algorithms are highlighted in Table 1. In particular, for each class of images the mean, max, and min values of the symmetry measure, the average and max processing time for each class are highlighted.

Tab. 1. Skeleton algorithm vs. Fourier descriptor-based contour algorithm

	Complete enumeration on 128 threads		Contour method based on the Fourier descriptor				Refinment of skeletal primitives chains alghnment
	J	time, sec	Q	Jq	J – Jq	time, sec	Ja	J – Ja	time, sec
mean	0.9407	40.75	0.0078663	0.8788	0.0619	0.47	0.8667	0.0740	0.71
RMS	0.0275	10.63	0.0028337	0.0710	–0.0435	0.08	0.1655	–0.1380	0.13
min	0.8647	24.38	0.003537	0.6212	0.2435	0.31	0.3182	0.5464	0.44
class #3 (65 objects)        max	0.9844	73.86	0.015681	0.9770	0.0075	0.69	0.9844	0.0000	0.93
mean	0.9483	56.90	0.007655	0.9358	0.0125	0.76	0.9426	0.0058	0.66
RMS	0.0204	7.10	0.0030141	0.0274	–0.0070	0.11	0.0269	–0.0065	0.15
min	0.8989	36.66	0.002582	0.8544	0.0446	0.53	0.8674	0.0315	0.48
class #4 (72 objects)        max	0.9869	71.53	0.015478	0.9833	0.0035	1.09	0.9869	0.0000	1.21
mean	0.9659	26.19	0.0042942	0.9564	0.0095	0.38	0.9642	0.0017	0.68
RMS	0.0102	9.24	0.0009783	0.0179	–0.0077	0.07	0.0105	–0.0003	0.06
min	0.9335	14.47	0.002001	0.8530	0.0804	0.30	0.9335	0.0000	0.57
class #5 (73 objects)        max	0.9898	62.86	0.007318	0.9831	0.0067	0.63	0.9898	0.0000	0.95
mean	0.8921	74.79	0.0178218	0.8061	0.0860	0.84	0.8223	0.0698	0.70
RMS	0.0253	19.90	0.005491	0.0916	–0.0663	0.22	0.1357	–0.1104	0.17
min	0.8284	46.92	0.008606	0.4863	0.3422	0.58	0.2248	0.6037	0.45
class #10 (59 objects)       max	0.9396	133.92	0.030189	0.9391	0.0005	1.48	0.9396	0.0000	0.96
mean	0.9456	56.51	0.0054881	0.9057	0.0399	0.62	0.9451	0.0006	0.75
RMS	0.0324	7.42	0.0038819	0.0912	–0.0587	0.21	0.0327	–0.0003	0.06
min	0.8526	41.58	0.001221	0.3036	0.5490	0.40	0.8526	0.0000	0.60
class #12 (63 objects)       max	0.9910	74.41	0.027541	0.9909	0.0001	1.59	0.9910	0.0000	0.97
mean	0.9404	76.22	0.0098355	0.8753	0.0652	0.67	0.9161	0.0244	0.73
RMS	0.0245	9.63	0.0036439	0.0766	–0.0521	0.13	0.0342	–0.0097	0.04
min	0.8516	55.67	0.00429	0.6369	0.2147	0.51	0.8216	0.0299	0.63
class #16 (56 objects)       max	0.9796	94.50	0.019049	0.9595	0.0201	1.43	0.9698	0.0097	0.81
mean	0.9351	42.82	0.0038465	0.8759	0.0592	0.50	0.7945	0.1406	0.83
RMS	0.0327	5.56	0.0018317	0.0603	–0.0276	0.06	0.1191	–0.0864	0.05
min	0.8112	25.46	0.000644	0.6553	0.1559	0.37	0.5394	0.2717	0.72
class #21 (60 objects)       max	0.9929	52.37	0.009304	0.9411	0.0518	0.70	0.9929	0.0000	0.95

Based on the available results we can conclude that the Fourier descriptor-based contour algorithm rarely finds the reference axis. In our experiments, the reference axes were found only in 4 of 448 processed images. Also, for some images, the axes were located diametrically opposed.

In general, if we just calculate the number of measures with the max accuracy and performance (highlighted cells in tab. 1), the Fourier descriptor-based con- tour algorithm scores 14 points while the alignment of skeletal primitives subchains method scores 21 points.

Below we analyze the cases where the compared approaches failed. Tab. 2 lists the failed cases of the Fourier descriptor-based contour algorithm for each class. The images in each class with the smallest Jaccard measure are shown. For comparison, the second axis that the Fourier descriptor-based contour algorithm was able to detect, and the result of the refinement algorithm based on skeletal primi- tive subchains for the same image are also included.

Tab. 2. Examples: images with the worst Jaccard measure for the Fourier descriptor-based contour algorithm

Class