Comparison of methods for initializing starting points on the optimization genetic algorithm

Introduction. The genetic algorithm of global optimization [1] differs from the others in Economics, Finance, and banking. In the genetic algorithm, points are represented as boolean sets. These lines can be formed in different ways: directly, using random sequences (with regular distribution law) or spreading points using random sequences (with a regular distribution law) in the space of real numbers, and then convert them into Boolean ones. The research is based on Acly function, Rastrigin function, Shekel function, Griewank function and Rosenbrock function. [2]. LP τ sequence [3], UDC sequence, uniform random spread are very interesting and efficient algorithms for spreading starting points. Recent studies in this area were carried out in the works [4]. These studies were applied to specific practical problems, there was no goal in averaging these parameters, in testing on a large number of practical problems of a complex type of the tested function [5]. LP τ sequences is a point spreading algorithm based on the matrix of irreducible Marshall Polynomials. UDC sequence is an algorithm for regular distribution of points over all coordinates in multidimensional space [6] regardless of the number of spread points [7]. Regular random spread [8] is a stochastic point spreading algorithm using the normal distribution law.

The best parameters of the genetic algorithm of global optimization were used [9].

Parameter description. The paper used the best parameters of the genetic algorithm of global optimization:

• 1.    Selection – tournament 4 participants.

• 2.    Recombination – 2-point, the probability of crossing – 0.8.

• 3.    Probability of mutation 0.001

• 4.    Binary coding.

Additional parameters used:

• 1.    The size of the space of the studied regularity – 2.

• 2.    Total number of spreading points (boolean sets) – 50.

• 3.    The maximum number of steps of the algorithm (generations) – 200.

• 4.    The accuracy of finding the extremum – 0.0001.

• 5.    The number of repeated runs of the algorithm – 400.

• 6.    Boundaries of the study area отfrom –45 to +45 on each coordinate.

We used six methods of initialization:

Method 1: using random sequences (with regular distribution law), a real number from 1 to 100 is obtained. If the resulting number is less than 50, the corresponding bit of the boolean set [10] takes the value 1, otherwise 0. This produces boolean sets (fig. 1).

Method 2: using random sequences [11], we obtain a real number from 1 to K, where K is the maximum real number obtained if each bit of the boolean set is equal to 1. Then, this real number is converted to a boolean set by the conversion rules. This produces boolean sets (fig. 2).

Method 3. The third method is equal to the first but with the checking of boolean sets for repeatability (fig. 3).

Method of initialization 1

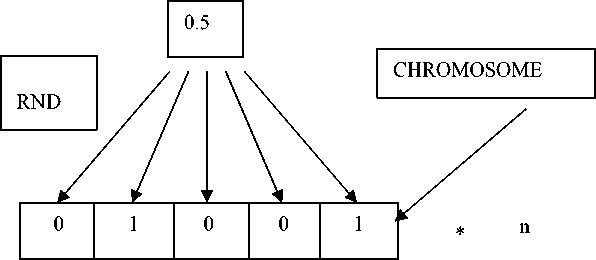
Fig. 1. The first method of initialization

Рис. 1. Первый способ инициализации

0

1

0

0

1

Fig. 2. The second method of initialization

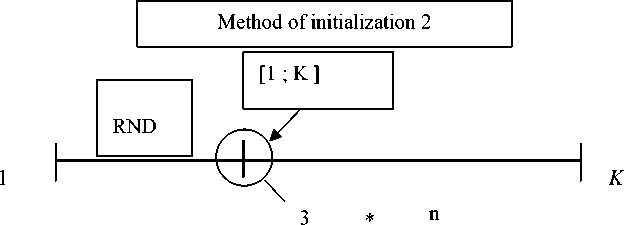
Рис. 2. Второй способ инициализации

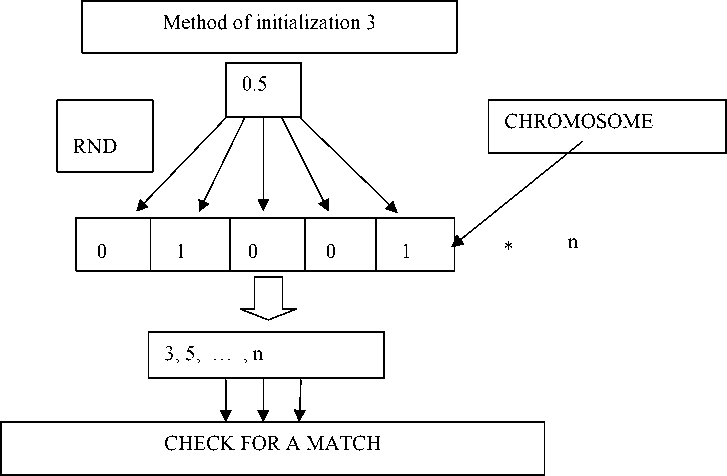
Fig. 3. The third method of initialization

Рис. 3. Третий способ инициализации

Method 4. The fourth method is equal to the second one but with the checking of real numbers for repeatability (fig. 4).

Method 5: with the help of the LP τ sequence, a real number from 1 to 100 is obtained. If the resulting number is less than 50, the corresponding bit of the boolean set will be 1, otherwise 0. This produces boolean sets (fig. 5).

Method 6: using the LP τ sequence, we obtain a real number from 1 to K, where K is the maximum real number obtained if each bit of the boolean set was equal to 1. Then, this real number is converted into a boolean set (fig. 6).

As a result, we get arrays of mathematical expectations and standard deviations of the solution quality for different functions and optimization algorithms [12]. The quality of the solution is the average error of finding the extremum [13].

Recent experiments in this area were carried out in the works of the scientist [7]. In his works, binary lines were formed without taking into account the check for repeatability.

Experimental part. The initialization methods are compared with each other on a genetic algorithm, according to math expectation, on the first function. The best way to initialize on a six-point scale is determined. Then they are compared on the second function, etc.

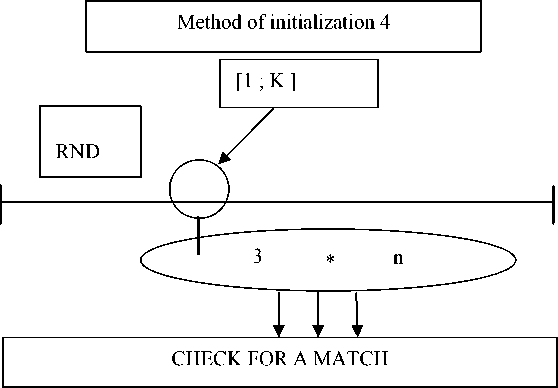
K

0

1

0

0

1

Fig. 4. The fourth method of initialization

Рис. 4. Четвёртый способ инициализации

Method of initialization 5

n

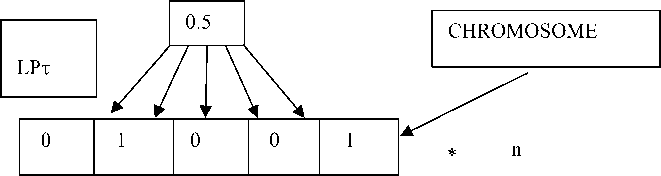
Fig. 5. The fifth method of initialization

Рис. 5. Пятый способ инициализации

Method of initialization 6

[ 1 ; K ]

LP τ

K

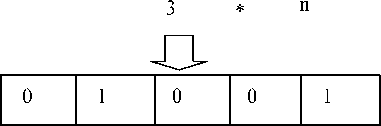
Fig. 6. The sixth method of initialization

*

n

Рис. 6. Шестой способ инициализации

Table 1

Percentage of finding the extremum for the algorithm by absolute value

		Method of initialization (I)						Best I
		1	2	3	4	5	6
ч 1 o' 9	1	4.00	3.50	2.75	2.25	3.50	3.25	1
	2	7.25	7.50	7.25	7.75	8.50	7.25	5
	3	0	0	0	0	0	0	–
	4	0	0.25	0	0.75	1.00	0.25	5
Total								5

Table 2

The quality of the solution for the Genetic algorithm by absolute value

Function		Method of initialization (I)						Best I by М	Best I by σ
		1	2	3	4	5	6
1	М	0.2431	0.2453	0.2511	0.2401	0.2231	0.2370	5	2
	σ	0.2127	0.2035	0.2221	0.2177	0.2076	0.2077
2	М	0.0613	0.0585	0.0629	0.0586	0.0533	0.0598	5	5
	σ	0.0512	0.0495	0.0725	0.0553	0.0310	0.0456
3	М	0.5001	0.5478	0.5091	0.4904	0.4433	0.4455	5	5
	σ	0.3947	0.5188	0.3718	0.3459	0.0055	0.0422
4	М	1.7635	1.7237	1.7866	1.7827	0.9066	1.9681	5	5
	σ	1.5675	1.7093	1.6367	1.6068	0.4152	1.8819
Places by М		5	4	6	2	1	3
Places by σ		3	3	5	4	1	2
Total		5	4	6	3	1	2

After that, the points obtained for all functions for each initialization method are summed up [14]. The larger the amount, the better place takes one or another method of initialization. The places got in this way are recorded in the tab. 1 and 2.

Then the whole cycle is repeated for the standard deviation ( σ ). After that, the obtained places by math expectation (M) and by σ are summed up and compared again [15]. Eventually we will know:

• 1.    The best initialization method for each of the functions when using a genetic algorithm, both by math expectation and by σ .

• 2.    The best and the worst methods of initialization on average for all four optimization functions, both by math expectation and by σ , and in general, when using a genetic algorithm.

Results. As we know, the goal of any optimization algorithm is to find the extremum as quickly, more accurately, cheaper and more reliable as possible.

The percentage of finding the extremum, on average, for all optimization functions is better for the initialization method 5 (tab. 2), it follows that the initialization method 5 has the greatest reliability (probability) of finding the extremum.

We prove that at 50 points, the algorithm calculates 200 steps (generations), on average, for 1/400 seconds.

Accuracy is the inverse of an error. The higher the accuracy, the smaller the error. The higher the accuracy obtained, the smaller the number takes the characteristic on a six-point scale, which means that the characteristic is better.

For the genetic algorithm (tab. 1) the smallest error of finding the extremum (quality of solution) according to the expected value for the first function characterizes the method of initialization 5, this means that the method 5 has the highest accuracy of finding the extremum. For the genetic algorithm, the initialization method 5 also has the highest accuracy of finding the extremum by mathematical expectation for the function 2–4. On average, for the genetic algorithm, the initialization method 5 has the highest accuracy of finding the extremum.

For the genetic algorithm, the smallest error of finding the extremum by σ for the function 1 (error) is in the initialization method 2, and for the function 2–4 – in the initialization method 5. On average, for a genetic algorithm, the smallest error is that the resulting expectation value is the average expectation value of the initialization method 5.

Since, on average, for the genetic algorithm, the highest accuracy of finding the extremum and the smallest error of the result obtained is in the initialization method 5, then, on average, the initialization method 5 is the best initialization method for the genetic algorithm and takes the first place.

To compare the method of initialization 5, for example, with the applied now numerical method of initialization 1, the comparison of these methods in percentage being conducted in relation to the method of initialize-tion 1 for each function, and then taken the arithmetic average of these percentages for all functions.

As a result, it became obvious that in the genetic algorithm, the initialization method 5 is better than the initialization method 1 by an average of 20 % and the application of check in boolean initialization does not lead to positive result, and in real – leads.

Conclusion. The genetic algorithm of global optimization based on Acly function, Rastrigin function, Shekel function, Griewank function and Rosenbrock function is analyzed. The research was carried out on six methods of initialization of boolean sets, using three algorithms of spreading initial points: LP τ sequence, UDC sequence, uniform random spread. Studies show that, on average, the initialization method 5 is the best initialization method for the genetic algorithm, and it follows that the initialization method 5 is very promising. It must be taken into account that the initialization method 5 is based on a non – random algorithm of spreading points LP τ sequence. This provides an incentive for further study of the LP τ sequence, and once again confirms its effectiveness.