Computer modeling of hot isostatic pressing process of porous blank

Hot isostatic pressing (HIP) is one of the most suitable techniques for producing the high-speed steel cemented carbide, superalloys, soft ferrites and composites at a simultaneous application of high-pressure and high temperature [1–3]. The governing of this advanced process is performed, as a rule, by computer. Therefore, development of more perfect mathematical models of the process of plastic deformation is the most important task of further improving the HIP technology and increasing the quality of new materials.

Two basic approaches to the construction of the mathematical model adequately describing the HIP process are generally used. The first method, a discrete one, is developed in the works [4–8]. Here, they consider different mechanisms of packing at HIP such, as plastic deformation, creeping, and diffusion described with kinetic equations. In the article [8] a porous material is modeled as a sphere with the spherical pore subjected to creeping deformation under isostatic loading conditions. However, introduction of the central symmetry considerably delays the packing process. It should be noted that there is a somewhat difficulty in application of the first method when modeling the HIP of workpieces having a complex configuration and shells which distort the uniformity of a stress-strain state of a porous body.

The second method, a continual one, is developed in [9–17]. Here, a porous body is considered as a complex packed medium with an irreversible volumetric strain. This allows to solve multidimensional problems of elasto-viscous-plastic flow of a porous body and a shell. In the work [17] the analyses of HIP technological modes based on the application of both the first and the second methods are given.

We have developed the continual approach. Unlike the works of other authors, the present investigation deals with the differential equations of motion introduced into the mathematical model instead of equilibrium equations. This allows to employ Lagrange’s method in numerical realization of the model by computer. The equations, in a special case, are written in the cylindrical coordinate system.

1.    Basic equations for computer modeling

The HIP process, in a general case, is a threedimensional non-stationary non-isothermal problem. Following the works [15–17] we have constructed simultaneous equations of motion describing the flow of a viscous-plastic isotropic compressible material subjected to strain hardening in the right-hand rectangular coordinate system x i . Denote in the equations: p is the density, t is the temperature, т is the time, v i is the component of the flow velocity vector, σ _i j , s _i j , ξ _i j are the components of stress tensors, a stress deviator, and strain rates. The basic equations have a form:

• –    the equation of motion ^^

• » ц:=сил;(1)

• –    the equation of continuity

^+ри = 0;(2)

• p    dx uv 7

• –    the equation of heat conductivity

• —    сP dl = (A grad г)(а + VOij^ij,(3)

where c is the specific heat, λ = λ(t, ρ) is the coeffi- cient of heat conductivity. The differentiation according to time is done along the path of motion of a material particle.

T h e c om pon en t s o f th e v e l oc ity v e ct or a n d t h ose o f t h e defor m a ti on rate a re de t e r m i n e d w i th t h e kn o w n relations:

idp + du ? + dv - _ p dx dz dr

-

dV r   ds— । d^ rz । ^P dx dr dz

v- r ’

Srr-See + 3a r dr ’

dV y    ds -z | ^^ zz | ^ rz | ^da dx dr dz r dz’

dx, ^;

^lj = - ^(v t,t + ^v i,i ).                                   (5)

The stress tensor, as usual, con sists of a sph e ri c al constituent and a deviator:

^a tj = ^a& tj + ^s tj ,

drdz

Tx^_V r , Tx^_V z ,

Srr _ 2^(dVL + ^^) rr        dr3p dx

^_2Ц(^ + ^^).

zz        dz3p dx

S_rz_^(^dV : + ^dV z ), ^rz dz ^r ’

,

,

where σ i s t he me a n n or m al stre ss, a n d δ ij is Kronecker’s symbol. The equations (1)– ( 6) a re c om pl e t e d w i th the rheological equations:

S tj = 2vG_lJ-;W              (7)

a = 3k,

v 1 dp. ^s ee ^_2^(₇- + ^pd; ⁾,

_ к dp p dx ’

T ² = ^{2      2      -}^ 4- ?²

i      ^s rr    ^s zz    ^s ee      ^s rz ,

F⁽T,a,a_s,q t ) _ 0.

where ξ i s th e ra t e of re l a t iv e c h a ng e o f volume, μ, k are coe f f icie n ts of sh ea r an d v ol ume t ri c v i sc os i ty de p e n de n t u pon de nsi ty a n d t em pe ra t u re .

The l o ad in g sur f ace, i n ge ner al cas e, ha s t he fo rm :

F ⁽T,o,o_s,q i ,^,q_n⁾ _ 0,                  (9)

The behavior of the metallic shell of the porous cylinder corresponds to the elasto-plastic flow of the material [18]. The differential equations have to satisfy the following initial and boundary conditions:

where T = ^s_t j S_t j i s th e i n t en s i ty o f t a ng en t i a l stresses, σ s is t h e y i e ld s t ress o f a sol i d p h a se o f t h e ma terial a n d i t is th e te m pera t u re f un c t i on , q i are work hardening parameters.

2. Mathematical model of HIP process

C on sider th e ma th e m ati c a l mode l of t h e HIP is o t h e rma l proce ss for a cyli n d ri c a l porou s body w i th the radius R and the height H w i th in a s h ell . Th e body su r f ac e i s su bje c t e d t o t h e pre ss u re of gas p = p_G (τ) at a st a ti on a ry te m pera t u re duri n g th e pre ssin g cy c l e . The simultaneous equations (1) – (9) describing the viscous-pla sti c fl o w o f a cyli n drica l porou s c o mpressible body is written as follows:

at t = 0, p = p o , Sy = 0, о = 0, v= 0;

at t ≥ 0 on the surface of the shell

σ = – p_G (τ), s_rr = s_zz = s_θθ = s_rz = 0.

Within the boundary of the porous body and the shell the condition of continuity of the velocity vector ῡ is assigned.

Solution of the equations is done by means of different schemes of continuous calculations of Wilkins’ type [18].

3. Results of numerical calculations

In numerical calculations the HIP process of a porous compressible high speed steel billet pressed in the hydrostat was modeled. The powder billet within

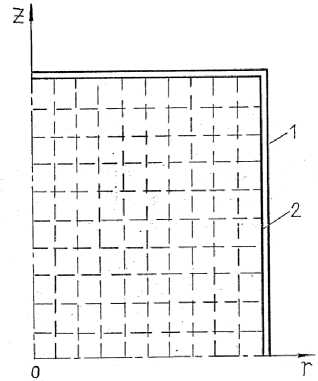
Fig. 1. Dynamics of a cylindrical porous body at HIP: p _G = 0–200 MPa, at a velocity of the pressure increase w , equal to 10 MPa/s

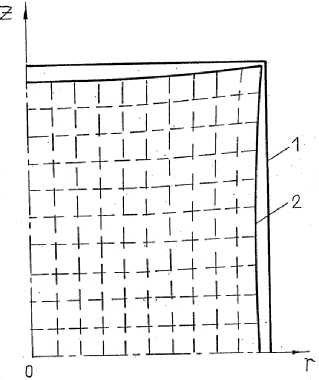
Fig. 2. Dynamics of a porous body at HIP: p _G = 0–200 MPa, w = 500 MPa/s, ρ₀ = 0,7 ρ _c

Порошковая металлургия и композиционные материалы

the mild steel shell was subjected to heating and then to hot gasostatic pressing.

The initial density of the porous body at HIP is assumed to be equal to 0.93ρ c , where ρ c is the density of non-porous high speed steel, and the process temperature being as high as 1300, 1400 and 1500 °C. The dependence p_G (τ) is taken as a piecewise linear one. The stress surface is assigned:

| г²+Д(р)а² = ^(рШО^)²,        (11)

where p = — is the relative density,

P c

/ i (p) = Q i (1 — p) ”¹ ,

A®^”2, f (0 = ®® + 1).

In Figs. 1 and 2 there are shown the cylindrical porous body at the initial instant (1) and final instant (2) in the HIP process as well as the difference grid on which the calculation is done. The coefficient values are taken from the works [7, 11].

Conclusion

The HIP process of a porous compressible body is described with the mathematical model based on differential equations of motion for a quasi-conti-nuous medium having an irreversible volumetric and shear deformation. The equations for a viscous- plastic isotropic porous hardening material are used as rheological ones. For the flows with an axial symmetry of the billet material after CIP the constitutive equations are written in the cylindrical coordinates. Numerical calculation of the problem for hardening the cylindrical high-speed steel billet within a mild steel shell is done using Lagrange’s method by means of the difference scheme of continuous calculation of Wilkins’ type.

Computer modeling allows to control the process of hardening and changing the form of a porous body at HIP in the course of time.