Consolidation model of powder magnetic materials

There are two basic approaches when modelling powder materials behavior under dynamic loadings. The first, heterogeneous one, considers the porous material to be the mixture of a compressible solid phase with a gas phase, the behavior of the material being modelled with interpenetrating and interacting continuums [1].

The second approach is based on representation of the multi-phase material as a quasicontinuum possessing joint integral properties of constituting phases [2–5]. In the case of negligible inertia effects the models of powder material compactness depend on the solutions of approximate differential equations of equilibrium.

The proposed models of die pressing powder magnetic materials are based on the solutions of differential equations of motion of a quasiisotropic compressible, elastic-plastic, hardening quasicontinuum with the ability to change both its form and volume.

Main equations

Let us consider the mathematical model of one-side pressing of powder magnetic materials in the form of hollow cylinder with radius R and height H. We will have a cylindrical coordinate system (r, θ, z) and the following notations: р - density, t - time, v - flow velocity vector, S – stress deviator. In the case of axial symmetry flowing when ve = 0, the initial values will not depend on θ.

Taking into account the above assumption the main equations of the model for the plane r , z can be written as

– equation of motion drT _ dSrr  dSrz Srr-S№   da

P dt dr     dz r      dr ’ d^z   dSrz | dSZZ | STZ । da P dt     dr dz r dz ’

– equation of deformation continuity

1 dp + dv_r + dr_z p dt dr dz

vr

.

r

The components of the flow velocity vector are defined from equations dr        dz dt_vr, dt_vz.

Differentiation with respect to time of equations (1)–(3) is carried out following the trajectory of motion of a material particle.

Physical equations characterizing the elasticplastic flow are chosen as rheological ones closing the system of equations. For elastic deformation these equations become:

dSrr       dVr ^dp dt ^ kdr   3p dJ’ dszz _ 2 /dvz + ^dp) dt " az 3p dt ’ dsee       Vr , ^dpk dt ^kr + 3pdt), d$rz         Sl^r   avz dt = ^\3z + ar), da _ К dp dt p dt’

where K and μ are modules of three-dimensional compression and shear respectively; σ is the average normal stress.

Equations (1)–(4) allow to consider the stressed-deformed state of the material relative to the cur- rent location of points, i.e. with deformation and stress increment parameters where derivatives of stress tensor components with respect to time are understood in terms of Yauman.

In the g en e ral c a s e t h e co nd i t io n o f p l ast i city is

F( T , σ, σ S , a 1 , …, a n ) = 0,                  (5)

where

Js_r ² r +S zZz + S j _e

T =

+ 2S²_Z

is the intensity of tangent stress; σS is the yield limit of solid-phase material; ai are hardening pa- rameters.

Mathematic model and results

The ma the ma ti c mode l ha s be e n de riv e d a nd implemented for one- side die pr ess ing of p owder ma g n et i c m at eri al s s u ch as bari u m ferri t es , Sm –Co and Nd–Fe–B i nt er me ta l lid e s by the punc h ac t ing with the applied force P .

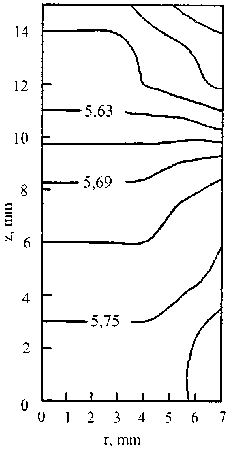
Fig. 1. Field of density distribution in Nd–Fe–B material after its pressing under p 0 = 8 t/cm², ρ 0 = 2,76 g/cm³

Fig. 1 shows the results of calculations when determining the field of density distribution in Nd–Fe–B material after its die pressing.

The formulation of mathematic problem reduced to finding the solutions of the differential equations (1)–(5) which must satisfy the following initial and boundary conditions:

– if t = 0, then ρ = ρ 0 , S rr = S θθ = S zz = S rz = 0, a = 0, v_r = v_z= 0;

– if t ≥ 0, then the normal stress σ zz = – p 0 is given for the working surface of the punch and the condition of adherence is assumed; the tangent stresses are given for the side surface of the die and the condition of nonpenetration is specified; for the bottom die surface the condition of adherence is assigned.

The solution of the problem stated is carried out with the difference scheme of continuous calculation like the Wilkins’ one [6]. The condition of plasticity (5) can be written as follows

|T2 + /1(p)^2 = (/2(p)/3(^)os)2,      (6)

where p is relative density,

/■i(p) = 6i(1-p)ni,

/2(P) = p”2 ,

/з(^) = № + 1.

Friction forces acting on the side surfaces of the die have been specified in the form of friction law т = /p. The coefficients b 1 , b 2 , n 1 , n 2 and n 3 have been calculated from the experiments.

Conclusion

In this paper the process of pressing powder magnetic materials such as barium ferrites, Sm–Co and Nd–Fe–B intermetallides has been described by mathematic model basing on differential equations of motion of the compressible quasicontinuum, subjected to irreversible threedimensional and shear deformations. The equations characterizing elastic-plastic, quasiisotropic, porous, hardening material were used as rheological ones. Numerical realization of the problem of die pressing powder magnetic materials into the form of hollow cylinders has been carried out with the help of difference scheme of continuous calculation as a Wilkins’ one.