Context-Sensitive Grammars and Linear-Bounded Automata

Published Online January 2016 in MECS

Phrase-structured grammars were proposed by N. Chomsky [1] and there are four types of grammars: Type 0 to Type 3. There are four types of languages corresponding to four types of grammar. These languages are known as recursive enumerable (Type 0), contextsensitive (Type 1), context-free (Type 2) and regular (Type 3). There are different automata proposed to recognize these languages. For example, context-sensitive languages are recognized by linear-bounded automata (LBA) [2, 3, 4].

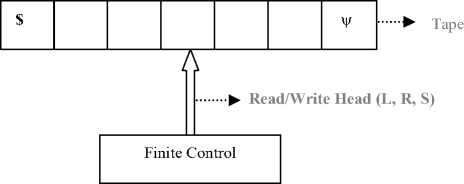
Fig.1. Model of Linear Bounded Automaton

A linear bounded automaton (LBA) is multi-track single tape Turing machine (TM) and its input tape length is in proportion of the input. The model of linear bounded automata (LBA) is shown in Fig. 1. It possesses a single track tape made up of cells that can contain symbols from an alphabet, a head that can read and write on the tape.

The head moves left or right on the tape utilizing finite number of states. A finite contiguous portion of the tape whose length is a linear function of the length of the initial input can be accessed by the read/write head. This limitation makes LBA a more accurate model of computers that actually exists than a Turing machine in some respects.

LBA are designed to use limited storage (limited tape). So, as a safety feature, we shall employ end markers ( $ on the left and ψ on the right) on tape and the head never goes past these markers. This will ensure that the storage bound is maintained and helps to keep LBA from leaving their tape. In case of multi-track tape, the first track is used for input always and other tracks are used for processing the input. But it does not mean that first track is read-only. Linear bounded automata can read and write on either of the tracks of the tape.

Linear bounded automata can be described by 5-tuples (Q, ∑ , δ , s, F), where

• (1)    Q is the finite and non-empty set of states,

• (2)    ∑ is the alphabet containing the blank symbol ( # ), two end markers symbols ‘$’ and ‘ ψ ’, but not containing the symbols L (left), R (right), and S(static). Symbols from this alphabet can be read or write (excluding end markers) on the tape,

• (3)    δ is the transition function which maps from

Q ×∑ (t i ) to (Q × ( ∑ (t i ) ∪ {L, R, S}) , where t i is the track on which symbol is to be read and write,

• (4)    s ∈ Q , it is the initial state or starting state,

• (5)    F ⊂ Q, it is the finite and non-empty set of final states

The configuration of a LBA, M=(Q, ∑ , δ , s, F) defined as a member of

Q ×∑ * ×∑× ( ∑ *-{ # }) , where # stands for blank

In other words, a configuration for single track LBA consist of present state, w1, a, and w2 where input string w=w1aw2 and symbol a is the present input symbol under the head, w1 is already read substring and w2 is the substring after the head. For example, (s, aa, a, ψ), (q, abab, b, aba) are two valid configurations. Suppose, if transition δ(s, a)=(q, b, R) then we have following relation

(s, $, a, bw ψ )    ^M (q, $a, b, w ψ )

where $ and ψ are left and right end markers respectively of the tape

If string w ∈ ∑ * is accepted by some LBA M if the head of M reaches the rightmost cell on the tape and processing ends in one of the final states. If the processing not ends in some of final states (F), the string is rejected. Such LBA are known as deterministic LBA (DLBA) by the definition given by J. Myhill [2]. The set of all strings accepted by M is known as language accepted by M also represented by L(M). The transition function of M is multivalued, in other words, for certain input symbol there is one or more transition. Such LBA are known as nondeterministic LBA (NLBA). We then mean by a string accepted by NLBA M, for which there is a processing of M which, given the string as an input ends up off the right end of the tape in a final state. On the other hand, a string w is said to be rejected by NLBA M if one of the following conditions occurs:

• (1)    Processing never ends

• (2)    Ends up off the left end of the tape

• (3)    Finally ends up off the right end of the tape in non-final state

The strings accepted by NLBA M are known as the languages accepted by M and the strings rejected by M are called the languages rejected by M. It is important to know that because of the non-determinacy characteristic of NLBA M, a certain string can be accepted or rejected both by M. When we say LBA it means NLBA in the rest of this chapter. So, readers are advised not to be confused about this unless it is specified.

Generally, LBA are non-deterministic automata. LBA are accepters for the class of context-sensitive languages. The only restriction placed on grammars for such languages is that no production maps a string to a shorter string. Thus no derivation of a string in a contextsensitive language can contain a sentential form longer than the string itself. Since there is a one-to-one correspondence between linear-bounded automata and such grammars, no more tape than that occupied by the original string is necessary for the string to be recognized by the automata.

• II. Related Work

  First time in 1960, John Myhill introduced the notion of deterministic linear bounded automata (DLBA) [2]. In 1963, Peter S. Landweber proved that the languages accepted by DLBA are context-sensitive languages [3]. In 1964, S. Y. Kuroda in his paper titled “Classes of Languages of & Linear-Bounded Automata”, Information and Control Journal, Vol. 7, pages 207-223 introduced the more general model which is known as nondeterministic linear bounded automata (NLBA) and showed that the languages accepted by NLBA are precisely the context-sensitive languages [4]. Later on so many research papers are published on LBA describing the decidability and undecidability problems. By combining the findings for Landweber [3] and Kuroda [4],

we say that a language is context-sensitive if and only if it is accepted by some linear-bounded automaton. But there is a requirement associated with the Kuroda’s theorem [4]. The grammar should be in a normal form which is known as Kuroda normal form (KNF). Kuroda [4] showed that a context-sensitive grammar can be converted into linear-bounded grammar and there is a linear-bounded automaton for it. There are many steps involved in conversion of a context-sensitive grammar into linear-bounded grammar namely

• (1)    Converting the given grammar into order 2,

• (2)    Converting order 2 grammar into length preserving grammar, and

• (3)    Converting length preserving grammar into linear-bounded grammar

The grammar G is said to be of order n if there appears no string of length greater than n in any production rule of the G. Kuroda proved that any context-sensitive grammar can be reduced to equivalent order 2 contextsensitive grammar [4].

A context-sensitive grammar is length-preserving if for any production rule α→β , it satisfies either of the following two conditions:

• (1)    α is the initial symbol

• (2)    β does not contain the initial symbol and lengths of α and β are equal

A context-sensitive grammar G is linear-bounded if it satisfies following conditions:

• (1)    G is order 2

• (2)    Length preserving and

• (3)    Production rule S → EF shows E=S, where S is the initial symbol of G

Lemma 1 (Kuroda Normal Form): For any contextsensitive grammar G of order 2, there exists a linear-bounded grammar G1 equivalent to G.

Proof: Let given grammar G=(V n , ∑ , P, S) and equivalent linear-bounded grammar G 1 =(V 1 , ∑ , P 1 , S 1 ). We defined the set of variables V 1 =V n ∪ {S 1 , Q} where Q is new variable and S₁ is initial symbol. The production rules of G₁ are defined by rules R₁, R₂ and R₃ [4].

Rule R₁ : New production rules to derive initial symbol of G

• S 1 → S 1 Q,

• S₁ → S where S is the initial symbol of G

Rule R 2 : New production rules for all symbols in (V n ∪ ∑ )

Q α→α Q,

α Q → Q α where α ∈ (V n ∪ ∑ )

Rule R₃ : For given production rules of G

A → B          if A → B is a rule in G,

AB → CD      if AB → CD is a rule in G,

AQ → BC      if A → BC is a rule in G

All the production rules of G₁ are linear-bounded. If G₁ derives string w eE *, it means Si =» w. It follows S=^w from rule R 1 . Therefore, L(G 1 ) c L(G). If the string w is derived by G then S =^ w it means SQⁿ > w is in G 1 . So by applying R 1 , we have S_i =» w. It means L(G) c L(G₁). Therefore, grammars G and G 1 are equivalent.

There is a proposal by Hoffcroft and Ullman [5] to design a linear-bounded automaton for a given contextsensitive grammar. The proposed LBA is two tracks automaton where the 1st track is used to hold the input and 2nd track is used to simulate the derivation of the given input applying the production rules of the grammar. But authors have not discussed in details how the derivation of the given string can be simulated on 2nd track. There are many concerns over the proposed model. For example, how intermediate sentential forms will be hold, how content on 2nd track will be shifted, how LBA recognize the variables to be replaced, etc.

I have proposed an algorithm to design a linear-bounded automaton for a context-sensitive grammar without converting the grammar into a normal form. The rest of the paper is organized as follows. Section III contains the proposed algorithm. Section IV contains the illustration based on the proposed algorithm and section V contains the conclusion and future study.

• III.    The Proposed Algorithm

Let context-sensitive (Type 1) grammar G = (Vn, E, P, S) has production rule of the form a^P such that |a|<|p| where a, Pe(VnuE)* and a has at least one element from Vn

Production rule S ^e (null) is there in G if S does not appear on right hand side of any production rule in G [5, 6, 7, 8, 9, 10].

Four tracks linear-bounded automaton M is used to simulate the derivation of a string produced by the context-sensitive grammar (CSG) G. The length of the tape is in order of the length of the input string. The first, second, third, and fourth tracks are used for input string, derivation using production rules of G, replacement, and replaceable sentence (RS) respectively.

Let us see the meaning and use of the terms derivation, replacement, and replaceable sentence (RS). Suppose P includes production rules {S ^ abc | aSAc, cA ^ Ac, bA ^ bb} where S, A e V_n, and a, b, c eE . The string w=aabbcc is produced by grammar G:

Table 1. Derivation, Replacement, and Replaceable Sentence

Production	Derivation	Replacement	Replaceable Sentence (RS)
S > a S Ac	aSAc	aSAc	S
> aab cA c	aabcAc	abc	S
> aa bA cc	aabAcc	Ac	cA
> aabbcc	aabbcc	bb	bA

It is clear from the above table that the suitable right hand side of a production rule is considered as replacement and the left hand side of the that production rule is considered as replaceable sentence (RS).

Suppose LBA M=(Q, E 1 , 5 , s, F) where E 1 Eu V n u J#} The LBA M is implemented based on the following algorithm.

Algorithm 1 (Context-sensitive Grammar G, Linear Bounded Automaton M)

• (1)    Input string is written on 1^st track. The initial symbol S is written on 2^nd track and 3^rd and 4^th tracks are blank.

• (2)    Repeat

• (i)    Read the 2^nd track from the left end and find out replaceable sentence (RS) and write on the 4^th track.

• (ii)    Write right hand side of the RS on 3^rd track.

• (iii)    Write content of 2^nd track which is after RS on the 3^rd track. If overflow occurs then EXIT with message “NOT ACCEPTED”.

• (iv)    Replace the RS on 2^nd track by the content of 3^rd track.

• (v)    Compare the contents of 1^st and 2^nd tracks. If contents are same then EXIT with message “ACCEPTED”.

• (vi)    Make the 3^rd and 4^th tracks blank.

It is clear from the above algorithm that M tries to simulate the right derivation for the input string on 2nd track. The 3rd track is used to hold the replacement for a RS. The 4th track is used to hold the current RS and find out the position of RS on the 2nd track. Without is it the steps in 2(iii) and 2(iv) of the proposed algorithm will not function correctly. Each time step 2(v) is executed, the contents of 1st and 2nd tracks are compared and if matched then LBA M accepts the input string. If overflow occurs in step 2(iii) then LBA terminates the process and string is rejected.

Theorem 1: If G=(V_n, E , P, S) is a context-sensitive grammar (CSG) then there is a linear bounded automaton (LBA) M which accepts L(G).

Proof: Suppose the G=(Vn, E, P, S) where Vn is nonempty finite set of variables, E is non-empty finite set of terminals, P is finite non-empty set of production rule and S is the starting symbol. LBA M implements the algorithm 1 as discussed above. Suppose there are n production rules of G and these are named as p1, p2, p3, …, pn such that pi: ai^Pi, PLi=ai, PRi=Pi where ai, Pi e(VnuE)* and ai has at least one element from Vn.

The starting symbol S is placed on 2^nd and 4^th tracks of M and suppose the right hand side PR_i of S is placed on 3^rd track provided that S > PR i is in G. M selects replacement from PR_i on 2^nd track and suppose the said replacement is PL j such that

S >a 1 PL j P 1 ^ PR , where a 1 , P 1 e (V_n uE )*

The replaceable sentence PL j is replaced on 2^nd track, that is, α 1 PR j β 1 where PL j ⇒ PR j is in G. This process is executed again and again till overflow occurs on 2^nd track or input on 1^st track is matched with content of 2^nd track.

Suppose the input string is derived the given grammar G in m-steps (m ≥ 1) such that

S ⇒ α ₁PL_i β ₁ ⇒ α ₂PL j β ₂ ⇒ α ₃PL_k β ₃… ⇒ α _mPL_q β _m ≡ w, where α _i, β _i ∈ (V_n ∪ ∑ )* and 1 ≤ i ≤ m.

The contents on 2^nd track after execution of step (2) of the proposed algorithm 1 are α ₁PL_i β ₁, α ₂PL j β ₂, α ₃PL_k β ₃…, α _mPL_q β _m. So, the step followed by LBA M is the same as adapted by the grammar G while producing the input string w. Since LBA M is non-deterministic automaton, so M can produce either the output “Acceptance” or “Rejection” for the same input. But it is believed that M follows the right replacement as adapted by the given grammar G. Therefore, the statement of the theorem is proved.

The length of the derivation for a string w does not go beyond the length of the string w. So, the length of tape is in order of the length of the input string. If the length of derivation on 2nd track goes beyond the length of the input string, it means either string w is not derived by G or LBA M does not follow the right replaceable sentence.

The space and time complexity of the LBA M are O(n) and O(n × m) respectively where n and m are length of input string and number of production rules in G respectively.

Lemma 1: If L is a context-sensitive language then there exists a linear bounded automaton M which accepts it.

Proof: Since for a context-sensitive language there is a context-sensitive grammar which generates it and it has been proved in algorithm 1 that languages generated by a context-sensitive grammar is recognized by a linear bounded automaton. Therefore the statement of the theorem is proved.

Lemma 2: If L 1 and L 2 are two context-sensitive languages then union of L 1 and L 2 is also a contextsensitive language (CSL).

Proof: We can prove it by using linear-bounded automata for L₁ and L₂. Let L₁ and L₂ are accepted by LBA M₁ and M₂ respectively as shown in Fig. 2(a) and Fig. 2(b). LBA M₁ and M₂ are designed based on the proposed algorithm. We construct a third LBA M₃ which follows either M 1 or M 2 as shown in Fig. 2(c) [5, 10]. LBA M 3 accepts a string if either M 1 accepts or M 2 accepts and rejects if either M 1 rejects or M 2 rejects. We can build LBA M 3 as a two tracks automaton. First and second tracks are used to simulate the behavior of M 1 and M 2 respectively. Obviously the language accepted by the M₃ is CSL. Therefore, union of two contest-sensitive languages is also contest-sensitive.

Input

M 1

Accept

Accept

Reject

Fig.2(b). LBA M 2

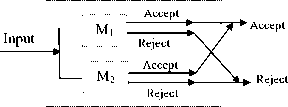
Fig.2(c). LBA M 3

Lemma 3: If G 1 and G 2 are two context-sensitive grammars (CSGs) then union of G 1 and G 2 is also a context-sensitive grammar.

Proof: (See the Lemma 1 and Lemma 2)

• IV.    Illustration

Let us consider the context-sensitive grammar G=({S, A}, {a, b, c}, {S → abc I aSAc, cA → Ac, bA → bb}, S). The LBA M=(Q, {a, b, c, S, A, #}, δ , s, F) be the automaton which accepts L(G). The production of the input string w=aabbcc by the grammar G is below:

Table 2. Context-sensitive Grammar

Production	Production Rule Used
S ⇒ a S Ac	S → aSAc
⇒ aab cA c	S → abc
⇒ aa bA cc	cA → Ac
⇒ aabbcc	bA → bb

Suppose the input string w=aabbcc is successfully accepted by LBA M. LBA M is implemented on above proposed algorithm. The tape contents in each step are given below:

Table 3. Contents after steps 1 and 2(i)

	1	2(i)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$S ψ	$S ψ
3rd Track
4th Track		$S ψ

Initially, the start symbol S is placed on 2nd track and input is on the 1st track. In step 2(i), the replaceable (RS) content on 2nd track is copied on 4th track. It means, start symbol S is copied on 4th track.

Table 4. Contents after steps 2(i) and 2(ii)

	2(ii)	2(iii)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$S ψ	$S ψ
3rd Track	$aSAc ψ	$aSAc ψ
4th Track	$S ψ	$S ψ

Reject

Fig.2(a). LBA M 1

The right hand side of RS (2nd track) is placed on the 3rd track in step 2(ii). It means aSAc is copied on 3rd track.

In step 2(iii), the content of 2nd track after RS is copied on the 3rd track. There is nothing to be copied and hence there is no question of overflow.

Table 5. Contents after steps 2(iv) and 2(v)

	2(iv)	2(v)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aSAc ψ	$aSAc ψ
3rd Track	$aSAc ψ	$aSAc ψ
4th Track	$S ψ	$S ψ

In step 2(iv), RS on 2nd track is replaced by content of 3rd track. Now, the contents of 1st and 2nd track are compared for possible production of the input string. We observe that contents of 1st and 2nd tracks are not equal and length of input is greater than the length of content on 2nd track. So, LBA M can further search for possible replacement. This is the completion of first round of production.

Table 6. Contents after steps 2(vi) and 2(i)

	2(vi)	2(i)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aSAc ψ	$a S Ac ψ
3rd Track
4th Track		$S ψ

If the desired string is not produced, the 3rd and 4th tracks are made blank. But contents of 2nd and 3rd tracks are unchanged. In next round, possible replaceable sentence (RS) is selected from 2nd track and written on 4th track which is S.

Table 7. Contents after steps 2(ii) and 2(iii)

	2(ii)	2(iii)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$a S Ac ψ	$aSAc ψ
3rd Track	$ abc ψ	$abc Ac ψ
4th Track	$S ψ	$S ψ

In step 2(ii), the suitable right hand side of the RS is placed on the 3rd track which is abc. The content of 2nd track after RS (Ac) is copied on the 3rd track in step 2(iii). Since there is no overflow, so LBA M can proceed further.

Table 9.Contents after steps 2(vi) and 2(i)

	2(vi)	2(i)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aabcAc ψ	$aab cA c ψ
3rd Track
4th Track		$cA ψ

LBA M makes the 3rd and 4th tracks blank in step 2(vi). Now in step 2(i), M finds RS (cA) on 2nd track and writes is on 4th track.

Table 10. Contents after steps 2(ii) and 2(iii)

	2(ii)	2(iii)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aabcAc ψ	$aabcAc ψ
3rd Track	$Ac ψ	$Ac c ψ
4th Track	$cA ψ	$cA ψ

In step 2(ii), LBA M finds the right hand side of RS and writes on 3rd track. LBA M copies the content after RS of 2nd on the 3rd track in step 2(iii). There is no overflow, so M can proceed further.

Table 11. Contents after steps 2(iv) and 2(v)

	2(iv)	2(v)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aab Acc ψ	$aabAcc ψ
3rd Track	$Acc ψ	$Acc ψ
4th Track	$cA ψ	$cA ψ

Now, M replaces the RS and content after RS on 2nd track by the content of 3rd track in step 2(iv). In step 2(v), M compares the contents of 1st and 2nd tracks and finds that contents are not equal. So, M can proceed further.

Table 12. Contents after steps 2(vi) and 2(i)

	2(vi)	2(i)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aabAcc ψ	$aa bA cc ψ
3rd Track
4th Track		$ bA ψ

LBA M makes the 3rd and 4th tracks blank in step 2(vi). LBA M searches for suitable RS on 2nd track and writes on 4th track in step 2(i). At this stage, RS is bA.

Table 8. Contents after steps 2(iv) and 2(v)

	2(iv)	2(v)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aabcAc ψ	$aabcAc ψ
3rd Track	$abcAc ψ	$abcAc ψ
4th Track	$S ψ	$S ψ

Table 13. Contents after steps 2(ii) and 2(iii)

	2(ii)	2(iii)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aabAcc ψ	$aabAcc ψ
3rd Track	$ bb ψ	$bb cc ψ
4th Track	$bA ψ	$bA ψ

In step 2(iv), the RS on the 2nd track is replaced by content of 3rd track (abcAc). Now, the contents of 1st and 2nd track are compared for possible production of the desired string in step 2(v). The contents of 1st and 2nd tracks are not equal, so LBA M can proceed further.

LBA M finds the right hand side of the RS (bA → bb) and places it on 3^rd track in step 2(ii). LBA M copies the content after RS of 2^nd on the 3^rd track in step 2(iii). There is no overflow, so M can proceed further.

Table 14. Contents after steps 2(iv) and 2(v)

	2(iv)	2(v)
1st Track	$aabbcc ψ	$aabbcc ψ
2nd Track	$aa bbcc ψ	$aabbcc ψ
3rd Track	$bbcc ψ	$bbcc ψ
4th Track	$bA ψ	$bA ψ

Now, M replaces the RS and content after RS on 2nd track by the content of 3rd track in step 2(iv). In step 2(v), M compares the contents of 1st and 2nd tracks and finds that contents are equal. So, M accepts the input and stops. Therefore, we say the LBA M simulates the derivation the input string.

• V.    Conclusion And Future Study

  I have proposed an algorithm to design a linear-bounded automaton (LBA) for a context-free grammar (CSG) without converting the grammar into a normal form. It avoids many steps in designing of linear bounded automata as compare to the proposal made by S. Y. Kuroda in 1964. The proposed algorithm exploits the nondeterminacy characteristic of the linear-bounded automata and selects an appropriate replacement while simulating the derivation of the input string. If appropriate replacement is not selected by a linear-bounded automaton, the input might be rejected even it is acceptable. So, an input string can be accepted or rejected both depending on the choice of replacement sentence (RS) considered by the linear-bounded automaton. For example, referring to the illustration discussed in Section IV, the string w=aabbcc will be rejected by the LBA M if LBA M selects the production rule S → abc at very first step. So, how to minimize wrong selection of production rules and RS by a LBA can be considered as further study.