Contours Matching with A Text-based Method

Published Online October 2013 in MECS DOI: 10.5815/ijmecs.2013.08.05

Intensity-based and Geometric-based methods are two general and most popular approaches for image matching. Intensity-based (color and texture), work with the intensity of the pixels and use the image itself as a feature descriptor. Geometry-based however, deal with the shape; they are feature-based method that extract points from the image (usually edge or corner points) and reduce the problem to point set matching. Users are more interested in matching and retrieval by shape than by color and texture [1][2][3][4].

Geometric methods are adapted to assumptions made about the illumination and viewpoint variations existing between two images. They determine the optimal matching of two patch-based image representation under rotation, scaling, and translations. Typically objects are subject to quite complex transformations when projected into an image plane. Therefore, the real transformations are approximated by easier transformations that can be mathematically treated with reasonable effort.

Different representations of shapes have been proposed these last years and used in the recognition process. The most known representations are based onto appearance [1], outline contour [2][3][4][5][6][7][8], aspect-graph [9][10], set of characteristic outline points [11], medial axis of silhouettes [12][13], shock graph [14][15], and shape axis trees (S-A-trees) [16]. A review of shape representation methods may be found in [17][18]. In [19], authors propose a part-based method for silhouettes representation. Silhouettes are partitioned into parts, junction and disjunction lines. Each element is then geometrically described. The obtained description is written following an XML language noted XLWDOS (XML Language for Writing Descriptors of Outline Shapes). Since real images are noisy, there XLWDOS descriptors may be very different. This sensitiveness to noise does not facilitate their use in the matching and recognition processes.

A notion of multi-scale descriptors of silhouettes is introduced to match silhouettes [20]. A Gaussian convolution of silhouettes is applied in order to smooth outline shapes and eliminate noise depending on the value of the Gaussian scale. Also, noisy XLWDOS descriptors of silhouettes may be matched using a reduction technique that eliminates noisy elements from the descriptors.

This paper is structured as follows:

We present in the second section an overview of the part-based method for describing outline shapes. In the third section we show the sensitiveness to noise of XLWDOS descriptors. In the fourth section, we explain our strategy based on the matching of XLWDOS descriptors using the reduction technique. The proposed method is validated using real images and the obtained results are presented and discussed in the fifth section.

• II.    Silhouettes Description

Concavity points for which direction of outer contour changes following top-bottom-top or bottom-top-bottom are considered as partition points (see Figure 1.a). A silhouette is partitioned at these points onto parts, junction and disjunction lines: either, two parts or more are joined with a third part through a junction line, or a part is joined with two parts or more through a disjunction line. This process applied to the left silhouette in Figure 1 produces seven parts, two junction lines and one disjunction line. The silhouette descriptor is the grouping of descriptors of its elements. A part is defined by its two boundaries (left and right) which begin at the highest left point and terminate at their lowest points (see Figure 1.b). Using the inflection points, these boundaries are segmented into a set of primitives (line, convex and concave contours) and described by the parameters: type (line, convex or concave curve), degree of concavity or convexity, angle of inclination and length. Junction and disjunction lines are decomposed onto segments. Each segment is described with three parameters: type, the reference numbers of parts where it appertains and its length. Types of segment are: Junction if it is common for two parts, Free-High if it belongs only to the high part or Free-Low if it belongs to the low part. Applying this description to write the descriptor of part P2 of the shape in the left of Figure 1, we obtain:

P₂^

2>cv 6% 56 76 cv 16% 107 77

This descriptor is read as follow: The left boundary of Part 2 is composed by a convex contour with 0.06 as degree of convexity, 56° of inclination and 76 pixels as length. The right boundary is composed by a convex contour with 0.16 as degree of convexity, 107° of inclination and 77 pixels as length.

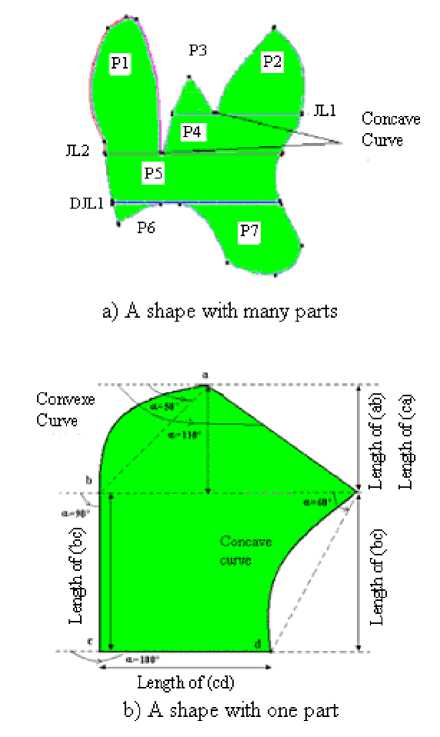
Fig. 1: Example of a silhouette, concave points, and parts

The notion of composed part is defined as a set of two (or more) parts joined to another part using a junction (or a disjunction) line and written as follows:

Composed Part^ Pi P₂....   P_n-1

Junction line P_n    / P1

Disjunction line P₂ P₃.... P_n

Recursively, a composed part is considered as a part and may constitute (with other elements) other composed parts.

There are three composed parts in the XLWDOS descriptor of the left silhouette in Figure 1:

• -    P2 P3 JL1 P4

• -     P1 P2 P3 JL1 P4JL2 P5

• - P1 P2 P3 JL1 P4JL2 P5 DJL1 P5 P6 .

To write descriptors of silhouettes we use the following syntax:

Silhouette ^Objectname> Name>Composed Part

(DXLWDOS means description according to XLWDOS description).

Finally, the descriptor of the silhouette in Figure 1 is:

Silhouette 1>

1>

r 165 8 cv 6% 100 120i>

2>

77

3>

4>

5>

6>

7>cc 10% 127 53 cv 7% 165 11r 115 38 cv 17% 48 26

• III.    Sensitiveness to Noise of XLWDOS Descriptors

XLWDOS descriptors are sensitive to noise which may produce additional parts, junction and disjunction lines. Noise may then change the global structure of XLWDOS descriptor, but in other cases it changes only the geometric description of its elements. Figure 2.b illustrates an example where noise produces in addition, two parts, one junction line, two other parts, and one disjunction line relatively to the shape 2.a. Also, noise may correspond to concave points that the change of position creates new parts and lines. The silhouette of Figure 2.d illustrates an example where a concavity point change of position produces additional parts and lines relatively to the shape 2.c.

Finally, the XLWDOS descriptors are robust to noise when it changes only the geometric description of contours; it is the case of the silhouette 2.e. Depending on the direction of computation of the XLWDOS descriptor; noise may change the global structure of XLWDOS descriptors.

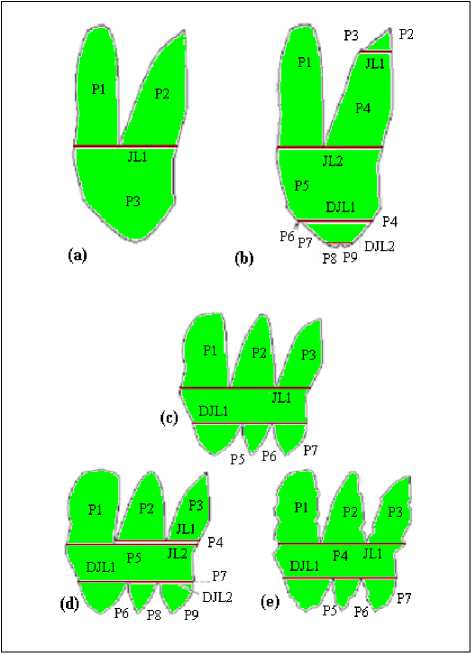
Fig. 2: Noisy outline shapes

• IV.    Matching descriptors of silhouettes4.1    Matching Descriptors in Multi Scale Space

• 4.2    Reduction Method

As it is described above, XLWDOS descriptors are sensitive to noise. Therefore, it is necessary to take into account this noise in the matching process. In a previous work we have developed a method comparing silhouettes at different scales [20] to eliminate noise from outline shape applying a convolution with a Gaussian filter. We obtain for each value of σ a smoothed outline shape. We define the notion of multiscale XLWDOS descriptors as the set of descriptors computed using these smoothed outline shapes obtained at different scales (values of σ) from the initial outline shape. More the value of σ increases, more the XLWDOS descriptor contains fewer elements whose number becomes steady from a certain value of σ [20]. In this present work, we will see that it is possible to find same results with textual transformation of descriptors without Gaussian Smoothing.

We define a noisy part, as a part whose length is 1, 2, 3 or n pixels. Each noisy part will be marked in the written descriptor using the two tags . For example, the XML structure of XLWDOS descriptors of silhouette 2.a and 2.b are:

Silhouette2a

Silhouette2b

< P3>

< /N>

These two descriptors cannot be matched because they have different structures. Therefore, the problem is to verify if we can reduce the two descriptors in order to maintain in their XML structures only their main parts. For this, we propose a reduction method that takes into account all possible positions of noisy parts in the XML structure.

Also, the XML structure of XLWDOS descriptors of silhouettes 2.c and 2.d are:

Silhouette2c

C>

Silhouette2d

>

<N>

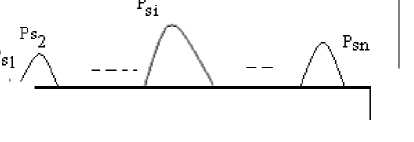
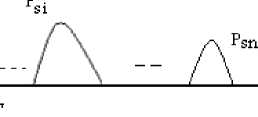
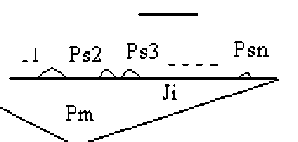
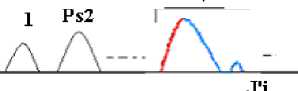
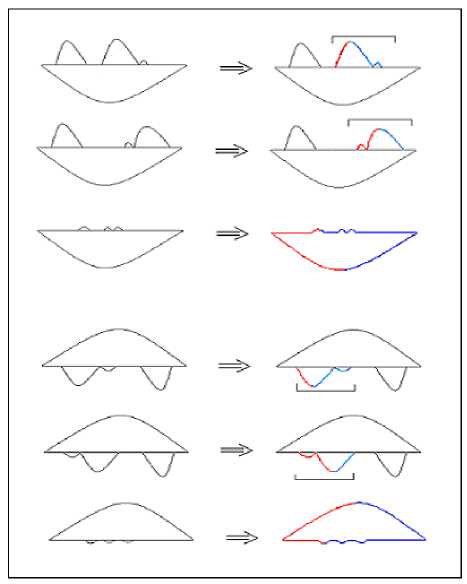
Fig. 6: Examples of descriptors reduction

For example, using the reduction method, the XML structure of XLWDOS descriptor of silhouette 2.d becomes:

Silhouette2d

P>

Now, the XML structure of both descriptors (Silhouette2c and Silhouette2d) are similar, therefore the matching of their elements may be done.

Other examples of transformations are given by graphic illustrations in Figure 6.

• V.    Experimentation

Different objects have been used to validate the proposed methods. We used many images taken in our laboratory (see Figure 7) and also some images of shapes built by B. Leibe and B. Schiele [21] where each object is represented by 41 views spaced evenly over the upper viewing hemisphere (see Figure 8).

Fig. 7: Objects used in experimentation

Fig. 8: A set of shapes of the database of Leibe and Schiele and some views of an object [21]

In Figure 9, we show two images of the same object (cup). There are parts and junction lines in the descriptor of the first image which could not be matched with other parts and lines in the descriptor of the second image.

After applying a convolution with a Gaussian filter for the two outline shapes, smoothed outlines shapes are obtained and the obtained XLWDOS descriptors of both two images become similar.

The matching problem has also been solved using our reduction method. The approach is been applied for the two noisy XLWDOS descriptors and gave same results. Indeed, the first noisy descriptor computed (of the first image) has the following structure:

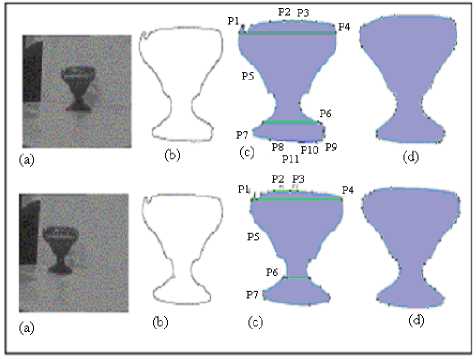
Fig. 9: For each image (a), the extracted outline shape of a cup (b), the result of applying XLWDOS description for outline shape (c) and the smoothed outline shape with σ=10 (d)

This descriptor is reduced as follows:

Cup2

<P1∪P2∪P3>∪P2∪P3>

∪P6∪P7>∪P6∪P7

>

Cup1

< N>

>

< P9>

This descriptor is reduced as follows:

Cup1

<P1∪P2∪P3>∪P2∪P3>

∪P6∪P7∪P8∪P10∪P11

∪P9>∪P6∪P7∪P8∪P10∪P11∪P9>

where: designates the part obtained as the union of the three parts P1, P2 and P3. Therefore the obtained descriptor may be written:

Cup1

<P’1>

The second noisy descriptor computed (of the second image) has the following structure:

Cup2

Therefore the obtained descriptor may be written:

Cup2

<P’’1>

Now both descriptors (of cup1 and cup2) can be matched and their similarity is obtained by comparing the elementary contours of the obtained parts.

Two other examples of experiments are given in Figures 10 and 11, the same process is applied and similar results are obtained. Indeed, the descriptors of smoothed shapes become similar.

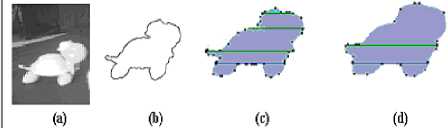
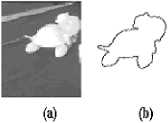
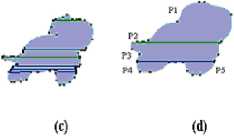
Fig. 10: Application of the reduction process on images of a turtle

For Figure 10, the two descriptors of the two objects to be matched are reduced to the following same descriptor:

∪P2>∪P2>< /P3>

∪P7>∪P7>

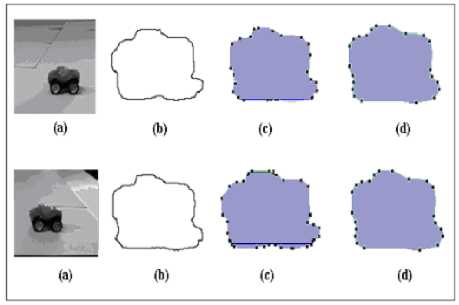
Fig. 11: Application of the reduction process on images of a turtle

In the same way, descriptors of silhouettes (a) and (b) in Figure 11 become:

∪P’3>

Other experiments of pairs of images give following descriptors for silhouettes that look alike after application of the reduction process. Same descriptors are therefore obtained for the compared outline shapes.

Fig. 12: Application of the reduction process on images of a banana

The obtained descriptors of silhouettes in Figure12 are:

∪P3>∪P 3>

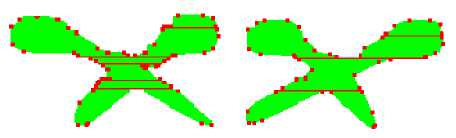
Fig. 13: Application of the reduction process on images of scissors

The obtained descriptors of silhouettes in Figure13 are:

∪P’7>

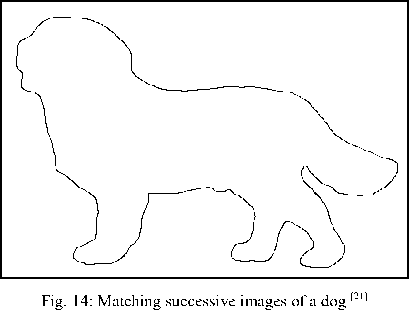
The obtained descriptors of silhouettes in Figure14 (from the data base of Leibe and Schiele [21]) are:

P1 P2 P3 J1 P4 J2 P5 D1 P6 D2 P8P9 D3 P10 P11 D4 P12 D5 P14 P15 P13 P7

• VI.    Conclusion

We proposed in this paper, an efficient method for silhouettes matching despite the presence of noise. The silhouettes are described according to the XLWDOS language. In order to permit a little difference in silhouettes shapes that generate unfortunately very different descriptors, a tolerance threshold is determined for XLWDOS descriptors by using thresholds for descriptors reducing and matching.

The proposed solution was illustrated by the writing of XLWDOS descriptors including the information of noisy parts. A reduction method has been developed in order to reduce their XML structures and let only main non-noisy parts.

Different positions of noisy parts were taken into account to achieve the matching process.

The conducted experiments show the usefulness of the proposed approach and demonstrate the possibility to use XLWDOS descriptors for real images applications.